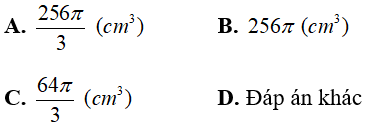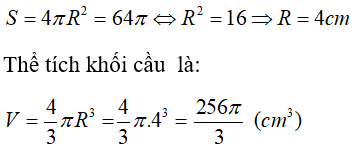Nội dung bài viết

    Xem thêm

    Công thức tính thể tích khối cầu chi tiết nhất – Toán 12

    Với Công thức tính thể tích khối cầu chi tiết nhất Toán lớp 12 Hình học chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ Công thức tính thể tích khối cầu chi tiết nhất biết cách làm bài tập Toán 12. Mời các bạn đón xem:

    1 921 24/07/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Công thức tính thể tích khối cầu chi tiết nhất - Toán lớp 12

    1. Công thức tính thể tích khối cầu

    - Khối cầu bán kính r có thể tích là : V=43πr3

    - Chú ý: Thể tích V của khối cầu bán kính r bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.

    2. Một số ví dụ

    VD1. Tính thể tích của khối cầu có bán kính bằng 5

    Lời giải:

    Thể tích khối cầu đã cho là V=43π.53=5003π

    VD2. Cho mặt cầu có diện tích là 96πa2. Tính thể tích của khối cầu đó.

    Lời giải:

    Diện tích mặt cầu là :

    S=4πr2=96πa2⇒r=26a

    Suy ra thể tích khối cầu là:

    V=43π.26a3=646π

    VD3. Cho hình chóp S.ABC có 4 đỉnh đều nằm trên một mặt cầu. Biết

    SA=a; SB=2a; SC=a và 3 cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu đó.

    Lời giải:

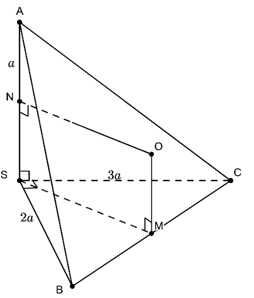
    Công thức tính thể tích khối cầu chi tiết nhất - Toán lớp 12 (ảnh 1)

    Ta có:

    SA⊥SBSA⊥SC⇒SA⊥SBC

    Do SBC là tam giác vuông nên trung điểm M của BC là tâm đường tròn ngoại tiếp

    Từ M kẻ đường thẳng ∆ vuông góc với (SBC) ⇒∆// SA

    Kẻ đường trung trực d của SA. d qua trung điểm N của SA và cắt ∆ tại O

    Khi đó O là tâm mặt cầu ngoại tiếp S.ABC.

    Tứ giác SNOM có 3 góc vuông nên là hình chữ nhật.

    ⇒r=SO=SN2+SM2

    Ta có

    BC=SB2+SC2=a13⇒SM=a132⇒r=a22+a1322=a142

    Diện tích mặt cầu là :

    S=4π.a1422=14πa2

    Thể tích mặt cầu là

    V=43π.a1423=7a3143π

    VD4. Cho hình chóp tam giác đều S.ABC có đáy cạnh a, mặt bên tạo với đáy góc 60∘. Tính thể tích khối cầu nội tiếp hình chóp đó.

    Lời giải:

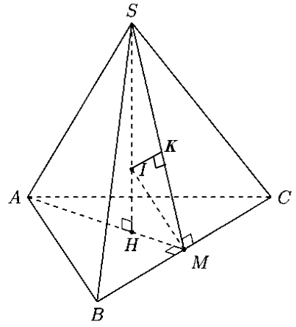
    Công thức tính thể tích khối cầu chi tiết nhất - Toán lớp 12 (ảnh 1)

    Gọi M là trung điểm BC.

    Gọi H là chân đường cao của hình chóp khi đó H là tâm đường tròn ngoại tiếp tam giác đều ABC ⇒HM=a36

    Gọi I là tâm mặt cầu nội tiếp S.ABC ⇒I∈SH

    Ta có:

    SBC∩ABC=BCAM⊥BCSM⊥BC⇒SBC,ABC=SMH^=60∘⇒SH=HM.tan60∘=a2

    Do I là tâm mặt cầu nội tiếp nên:

    r=dI,ABC=dI,SBC⇔IH=IK

    ⇒MI là phân giác SMH^

    Theo tính chất phân giác ta có:

    IS​IH=SMHM⇔SHIH=SM+HMHMSM=SH2+HM2=a24+a212=a33⇒SM+HMHM=3

    Do đó: SHIH=3⇒r=IH=a6

    Vậy thể tích khối cầu là V=43π.a63=πa3162

    3. Bài tập vận dụng

    Bài 1: Cho hình cầu có diện tích mặt cầu là 64π (cm2). Tính thể tích khối cầu?

    Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

    Lời giải:

    Ta có:

    Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

    Chọn đáp án A.

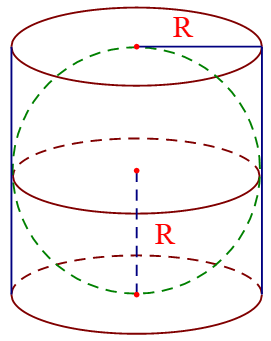
    Bài 2: Cho một hình cầu nội tiếp trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy bà bán kính đáy hình trụ bằng bán kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ

    Trắc nghiệm Hình cầu. Diện tích mặt cầu và thể tích hình cầu có đáp án

    Giải

    Từ đề bài suy ra chiều cao của hình trụ là h = 3R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ

    Trắc nghiệm Hình cầu. Diện tích mặt cầu và thể tích hình cầu có đáp án

    Bài 3: Thể tích khối cầu ngoại tiếp hình lập phương 9 cm là bao nhiêu?

    Lời giải

    Gọi R là bán kính khối cầu ngoại tiếp hình lập phương ABCD.EFGH

    Ta có: CE = AB . 3 = 9 cm. Suy ra R =1/2 CE = 4,5 cm

    Thể tích khối cầu là: V = 4/3 . 3,14 . 4,52 = 84.78 cm3

    Vậy thể tích khối cầu là 84,78 cm3

    Bài 4: Cho một hình cầu nội tiếp trong hình trụ. Biết trằng đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.

    Giải:

    Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên h = 2R với R là bán kính hình cầu và cũng là bán kính đáy của hình trụ.

    Thể tích của hình cầu : V cầu = 4/3 . Pi . R3

    Thể tích khối trụ V trụ = pi. R2 . 2 R = 2 . Pi. R3

    Tỉ số thể tích hình cầu và thể tích hình trụ là: V cầu / V trụ = 2/3

    Bài 5: Cho hình lập phương ABCD.A'B'C'D'. Tính thể tích khối cầu.
    a) Ngoại tiếp hình lập phương
    b) Nội tiếp hình lập phương.
    Giải

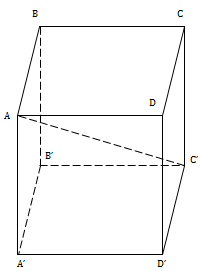
    a) Bán kính khối cầu ngoại tiếp hình lập phương là
    R=12AC′=12a2+a2+a2=a32
    V1=43πR3=43π.a3.338=a3π.32(đvtt)

    b)
    Khối cầu nội tiếp hình lập phương có bán kính

    2r=a⇔r=a2
    Thể tích khối cầu
    V2=43π.r3=43π.a38=πa36 (đvtt)

    Bài 6: Thể tích của khối cầu sẽ thay đổi như thế nào nếu.
    a) Tăng bán kính lên k lần.
    b) Giảm bán kính k lần.

    Bài 7: Cho hình chóp S.ABC có . H, K l3 h/c của A trên SB, SC.
    a) CMR: 5 điểm A, B, C, H, K cùng thuộc một mặt cầu.
    b) Tính thể tích khối cầu đó.

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 921 24/07/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: