Công thức tính diện tích mặt cầu, thể tích khối cầu (2024) chi tiết nhất
Với Công thức tính diện tích mặt cầu chi tiết nhất Toán lớp 12 Hình học chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ Công thức tính diện tích mặt cầu chi tiết nhất biết cách làm bài tập Toán 12. Mời các bạn đón xem:
Công thức tính diện tích mặt cầu, thể tích khối cầu chi tiết nhất
I. Lý thuyết mặt cầu
1. Mặt cầu là gì?
Tập hợp các điểm trong không gian cách điểm O cố định một khoảng không đổi r (r > 0) được gọi là một mặt cầu tâm O bán kính r.
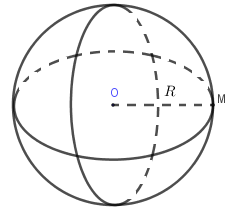
Kí hiệu: S(O;R) = {M|OM = R}
* Cho mặt cầu S (O; r) và điểm A trong không gian.
- Nếu OA = r thì điểm A nằm trên mặt cầu
- Nếu OA < r thì điểm A nằm trong mặt cầu.
- Nếu OA > r thì điểm A nằm ngoài mặt cầu.
2. Tính chất của mặt cầu
Nếu điểm ngoài mặt cầu thì:
- Qua có vô số tiếp tuyến với mặt cầu.
- Độ dài các đoạn thẳng nối với các tiếp điểm đều bằng nhau.
- Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
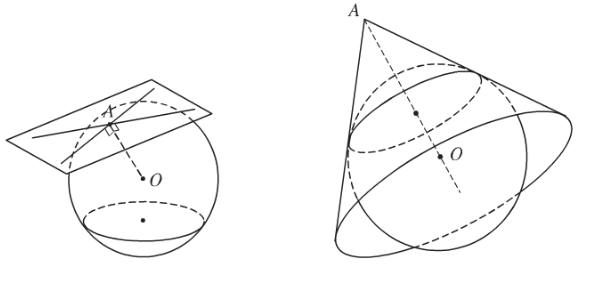
3. Vị trí tương đối của mặt cầu với đường thẳng
Cho mặt cầu tâm , bán kính và đường thẳng , gọi là hình chiếu của trên .
+ Nếu thì cắt tại điểm phân biệt.
+ Nếu thì cắt tại một điểm duy nhất . ( là tiếp tuyến với mặt cầu, là tiếp điểm)
+ Nếu thì và không có điểm chung.
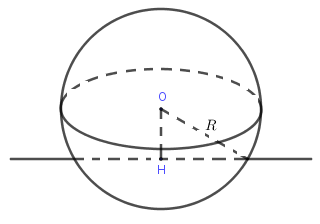
4. Vị trí tương đối của mặt cầu với mặt phẳng
Cho mặt cầu tâm , bán kính và mặt phẳng , gọi là hình chiếu của trên .
+ Nếu thì cắt theo đường tròn tâm và bán kình .
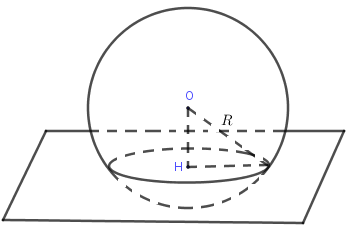
+ Nếu thì tiếp xúc tại tiếp điểm .
+ Nếu thì và không có điểm chung.
Đặc biệt: Nếu thì đường tròn giao tuyến của và được gọi là đường tròn lớn, được gọi là mặt phẳng kính.
5. Tiếp tuyến với mặt cầu
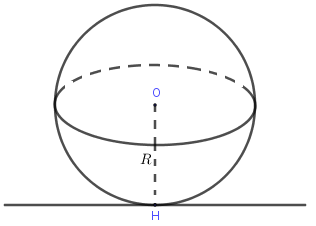
- Qua một điểm nằm trong mặt cầu không vẽ được tiếp tuyến nào với mặt cầu.
- Qua một điểm nằm trên mặt cầu vẽ được vô số tiếp tuyến với mặt cầu tại điểm đó. Tập hợp các tiếp tuyến chính là mặt phẳng tiếp diện của mặt cầu.
- Qua một điểm nằm ngoài mặt cầu vẽ được vô số tiếp tuyến với mặt cầu. Tập hợp các tiếp điểm với mặt cầu là đường tròn nằm trên mặt cầu.
II. Công thức tính diện tích mặt cầu, thể tích khối cầu
1. Công thức tính diện tích mặt cầu
- Cho mặt cầu (S) có bán kính r.
Khi đó diện tích mặt cầu
- Chú ý: Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.
2. Công thức tính thể tích khối cầu
Khối cầu bán kính r có thể tích là V =
3. Một số ví dụ
VD. Tính diện tích mặt cầu (S) và thể tính khối cầu (V) có bán kính là 3.
Lời giải:
Diện tích mặt cầu là
Thể tích khối cầu là V = =36
III. Các dạng bài về mặt cầu và cách giải
Dạng 1. Xác định tâm và bán kính mặt cầu ngoại tiếp hình lăng trụ đứng
Ta xác định tâm O và O' của hai đáy
Tâm của mặt cầu ngoại tiếp lăng trụ lúc này chính là trung điểm của OO'
R = IA =
Chú ý: Hình lăng trụ nội tiếp trong một mặt cầu khi nó là hình lăng trụ đứng và có đáy đa giác nội tiếp.
Mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' có:
- Tâm là trung điểm AC'
- Bán kính R = =
Khi ABCD.A'B'C'D là hình lập phương: R =
Dạng 2. Mặt cầu ngoại tiếp hình chóp
Để xác định tâm của mặt cầu ngoại tiếp hình chóp, chúng ta thực hiện theo các bước sau:
- Tìm tâm O của mặt đáy
+ Trong tam giác đều: Giao điểm của 3 đường trung tuyến
+ Hình vuông và hình chữ nhật: Giao điểm 2 đường chéo
+ Tam giác vuông: Trung điểm của cạnh huyền
- Dựng một trục d là đường thẳng đi qua O và vuông góc với đáy (d song song với chiều cao hình chóp)
- Ta sẽ xác định mặt phẳng trung trực (P) của một cạnh bên
- Giao điểm của mặt phẳng (P) và d là tâm của mặt cầu ngoại tiếp
IV. Bài tập vận dụng
Bài 1. Cho mặt cầu (S) tâm O có diện tích là . Một mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có chu vi là . Tính khoảng cách từ O tới (P).
Lời giải:
Diện tích mặt cầu (S) là:
Bán kính của đường tròn thiết diện là
Suy ra :
Bài 2. Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a. Tính diện tích mặt cầu ngoại tiếp hình lăng trụ đã cho.
Lời giải:
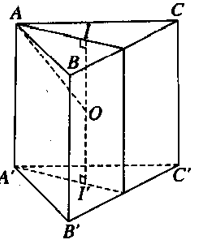
Gọi I và I’ lần lượt là trọng tâm của hai đáy lăng trụ. Suy ra I và I’ đồng thời cũng là tâm của 2 đường tròn ngoại tiếp các tam giác đáy.
Do ABC.A’B’C’ là lăng trụ đều nên II’ chính là trục của lăng trụ
Do đó tâm O của mặt cầu ngoại tiếp nằm trên II’.
Kẻ đường trung trực d của AA’. Dễ thấy d cắt II’ tại trung điểm của II’
Vậy O là trung điểm của II’
Ta có :
Do đó diện tích mặt cầu :
Bài 3. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Đường cao
Xác định tâm, bán kính và tính diện tích mặt cầu nội tiếp hình chóp S.ABCD.
Lời giải:
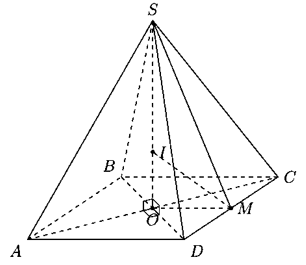
Gọi O là tâm hình vuông ABCD.
Gọi I là tâm mặt cầu nội tiếp hình chóp S.ABCD
Do I là tâm mặt cầu nội tiếp nên tức là MI là phân giác của
Theo tính chất đường phân giác ta có tỉ số:
Ta có:
Suy ra:
Vậy mặt cầu nội tiếp hình chóp là mặt cầu
Diện tích mặt cầu là:
Xem thêm tổng hợp công thức môn Toán lớp 12 đầy đủ và chi tiết khác:
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12
