50 bài toán về tiếp tuyến của đồ thị hàm số và cách giải (có đáp án 2024) – Toán 12
Với cách giải các dạng toán về Tiếp tuyến của đồ thị hàm số và cách giải bài tập môn Toán lớp 12 Giải tích gồm phương pháp giải chi tiết, bài tập minh họa có lời giải và bài tập tự luyện sẽ giúp học sinh biết cách làm bài tập các dạng toán về Tiếp tuyến của đồ thị hàm số và cách giải bài tập lớp 12. Mời các bạn đón xem:
Tiếp tuyến của đồ thị hàm số và cách giải bài tập - Toán lớp 12
A. LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI.
1. Phương pháp giải.
Bài toán 1: Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm thuộc đồ thị hàm số.
Cho hàm số và điểm . Viết phương trình tiếp tuyến với (C) tại M.
Bước 1: Tính đạo hàm . Tìm hệ số góc của tiếp tuyến là .
Bước 2: Phương trình tiếp tuyến tại điểm M là:
Lưu ý:
- Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ thì khi đó ta tìm bằng cách thế vào hàm số ban đầu, tức Nếu đề cho ta thay vào hàm số để giải ra .
- Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị và đường thẳng Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành độ giao điểm giữa d và (C)
Bài toán 2: Viết phương trình tiếp tuyến của đồ thị hàm số có hệ số góc k cho trước.
Bước 1: Gọi là tiếp tuyến cần tìm có hệ số góc k.
Bước 2: Giả sử là tiếp điểm. Khi đó thỏa mãn: (*) .
Bước 3: Giải (*) tìm . Suy ra .
Bước 4: Phương trình tiếp tuyến cần tìm là:
Lưu ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:
- Tiếp tuyến hệ số góc của tiếp tuyến là
- Tiếp tuyến hệ số góc của tiếp tuyến là
- Tiếp tuyến tạo với trục hoành một góc thì hệ số góc của tiếp tuyến là
Bài toán 3: Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến đi qua điểm
Cách 1.
Bước 1: Phương trình tiếp tuyến đi qua hệ số góc k có dạng
Bước 2: d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
Bước 3: Giải hệ này tìm được x suy ra k và thế vào phương trình , ta được tiếp tuyến cần tìm.
Cách 2.
Bước 1. Gọi là tiếp điểm và tính hệ số góc tiếp tuyến theo
Bước 2. Phương trình tiếp tuyến có dạng: . Do điểm nên giải phương trình này ta tìm được .
Bước 3. Thế vào ta được tiếp tuyến cần tìm.
Bài toán 4 : Viết phương trình tiếp tuyến chung của hai đồ thị hàm số và .
Bước 1. Gọi d tiếp tuyến chung của và là hoành độ tiếp điểm của d và thì phương trình d có dạng
Bước 2. Dùng điều kiện tiếp xúc của d và , tìm được .
Bước 3. Thế vào ta được tiếp tuyến cần tìm.
Lưu ý:
- Hệ số góc của tiếp tuyến với (C) tại điểm thuộc (C) là:
- Cho đường thẳng
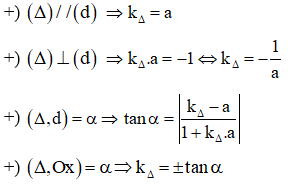
- Tiếp tuyến tại các điểm cực trị của đồ thị (C) có phương song song hoặc trùng với trục hoành.
- Cho hàm số bậc 3:
+) Khi a > 0: Tiếp tuyến tại tâm đối xứng của (C) có hệ số góc nhỏ nhất.
+) Khi a < 0: Tiếp tuyến tại tâm đối xứng của (C) có hệ số góc lớn nhất.
2. Công thức tính nhanh.
Bài toán 1: Cho hàm số có đồ thị (C). Phương trình tiếp tuyến tại M thuộc (C) và I là giao điểm 2 đường tiệm cận. Ta luôn có:
- Nếu thì chỉ tồn tại 2 điểm M thuộc 2 nhánh của đồ thị (C) đối xứng qua I và .
Cách nhớ:
- M luôn là trung điểm của AB(với A,B là giao điểm của với 2 tiệm cận).
- Diện tích tam giác IAB không đổi với mọi điểm M và .
- Nếu E,F thuộc 2 nhánh của đồ thị (C) và E,F đối xứng qua I thì tiếp tuyến tại E,F
song song với nhau (suy ra một đường thẳng d đi qua E,F thì đi qua tâm I).
Chứng minh:
- Ta có ; là giao điểm của 2 tiệm cận.
- Gọi . Phương trình tiếp tuyến tại M có dạng:
Ta có:
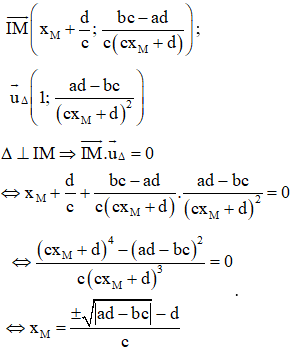
Lại có:
- Giao điểm của với tiệm cận ngang là .
- Giao điểm của với tiệm cận đứng là .
- Xét :
Vậy M luôn là trung điểm của AB.
Ta có:
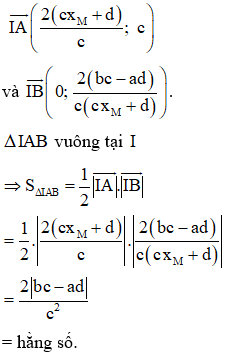
Vậy diện tích không đổi với mọi điểm M.
Ta có:
- Gọi

Từ (1) và (2) suy ra .
Bài toán 2: Cho hàm số có đồ thị là (C), . Gọi điểm trên (C) biết tiếp tuyến của (C) tại điểm M cắt các trục lần lượt tại A,B sao cho . Khi đó thoả mãn .
Chứng minh:
- Xét hàm số , .
Ta có
- Gọi là điểm cần tìm. Gọi tiếp tuyến với (C) tại M ta có phương trình :
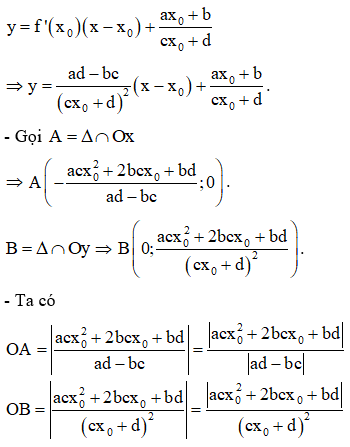
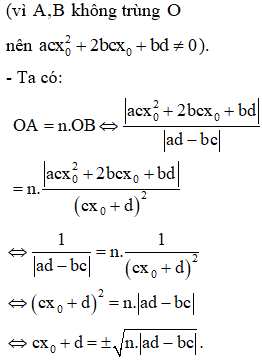
B. VÍ DỤ MINH HOẠ.
Ví dụ 1. Tiếp tuyến của đồ thị hàm số tại điểm H có tung độ bằng 21 có phương trình là:
A.
B.
C.
D. .
Lời giải
Gọi H(x0 ;y0) ta có y0 = 21 nghĩa là
Giải phương trình:
Đồng thời , suy ra:
Vậy có hai tiếp tuyến cần tìm là và .
Chọn B.
Ví dụ 2. Phương trình tiếp tuyến của đồ thị hàm số tại điểm là
A.
B.
C.
D. .
Lời giải
Theo giả thiết ta có và →
Vậy phương trình tiếp tuyến là .
Chọn B.
Ví dụ 3. Cho hàm số có đồ thị là . Gọi điểm với là điểm thuộc biết tiếp tuyến của tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A,B và tam giác OAB có trọng tâm G nằm trên đường thẳng . Hỏi giá trị của bằng bao nhiêu?
A.
B.
C.
D.
Lời giải
- Gọi với là điểm cần tìm.
- Gọi tiếp tuyến của (C) tại M ta có phương trình.
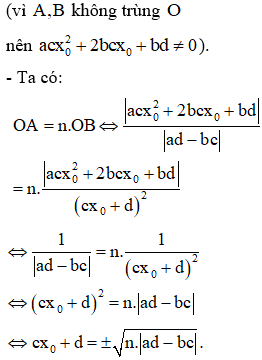
- Khi đó tạo với hai trục tọa độ có trọng tâm là

Chọn A.
C. BÀI TẬP TỰ LUYỆN.
Câu 1. Phương trình tiếp tuyến của đường cong tại điểm là:
A.
B.
C.
D. .
Câu 2. Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 2, có hệ số góc:
A. -1
B. -3
C. 3.
D. 5.
Câu 3. Gọi (C) là đồ thị của hàm số . Có hai tiếp tuyến của (C) cùng có hệ số góc bằng . Đó là các tiếp tuyến:
A. hoặc .
B. hoặc .
C. hoặc .
D. hoặc .
Câu 4. Cho hàm số có đồ thị là (C). Trong số các tiếp tuyến của (C), có một tiếp tuyến có hệ số góc nhỏ nhất. Hệ số góc của tiếp tuyến này bằng:
A. -3,5
B. - 5,5
C. - 7,5
D. -9,5
Câu 5. Cho hàm số có đồ thị (C). Tiếp tuyến của (C) song song với đường thẳng có phương trình:
A.
B.
C.
D.
Câu 6. Cho hàm số có đồ thị là (C). Gọi là tiếp tuyến của (C) tại điểm A(1;5) và B là giao điểm thứ hai của với V. Diện tích tam giác OAB bằng:
A. 5.
B. 6
C. 12
D. .
Câu 7. Cho hàm số có đồ thị (C). Gọi d là tiếp tuyến của (C), biết d đi qua điểm A(4;-1). Gọi M là tiếp điểm của d và (C), toạ độ điểm M là:
A.
B.
C. .
D. .
Câu 8. Cho hàm số có đồ thị (C). Trong tất cả các tiếp tuyến của (C), tiếp tuyến thỏa mãn khoảng cách từ giao điểm của hai tiệm cận đến nó là lớn nhất, có phương trình:
A. hoặc .
B. hoặc .
C. hoặc
D. hoặc .
Câu 9. Từ điểm kẻ đến đồ thị hàm số hai tiếp tuyến vuông góc nhau thì tập tất cả các giá trị của m bằng:
A. hoặc .
B. hoặc .
C. hoặc .
D. hoặc .
Câu 10. Cho hàm số có đồ thị (C). Tập tất cả các giá trị của tham số m để tiếp tuyến của (C) tại giao điểm của (C) và đường thẳng song song với đường thẳng là?
A.
B.
C.
D.
Câu 11. Cho hàm số có đồ thị là (C). Tại điểm thuộc (C), tiếp tuyến của (C) song song với đường thẳng . Khi đó biểu thức liên hệ giữa a và b là:
A.
B.
C.
D.
Câu 12. Cho hàm số có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm song song với đường thẳng . Khi đó giá trị của a + b bằng:
A. 2.
B. 1.
C. -1.
D. 0.
Câu 13. Cho hàm số có đồ thị là (C). Nếu (C) đi qua A(3;1) và tiếp xúc với đường thẳng , thì các cặp số (a;b) theo thứ tự là:
A. hoặc .
B. hoặc .
C. hoặc .
D. hoặc .
Câu 14. Cho hàm số có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt (M,N khác A) thỏa mãn
A. 0.
B. 2
C. 3
D. 1
Câu 15. Tiếp tuyến của đồ thị hàm số tại điểm D có hoành độ bằng 2 có phương trình là
A.
B.
C.
D.
Câu 16. Tiếp tuyến của đồ thị hàm số tại điểm I có tung độ bằng 1 có phương trình là
A.
B.
C.
D. .
Câu 17. Tiếp tuyến của đồ thị hàm số có hệ số góc bằng có phương trình là
A.
B.
C. .
D. .
Câu 18. Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến có hệ số góc bằng 4.
A.
B.
C. .
D. .
Câu 19. Cho hàm b có đồ thị là (C). Tiếp tuyến của đồ thị (C) vuông góc với đường thẳng có phương trình là:
A.
B.
C.
D. .
Câu 20. Có bao nhiêu tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị với trục Ox ?
A. 4.
B. 2.
C. 1.
D. 3.
Câu 21. Gọi là tiếp tuyến của đồ thị hàm số (C): tại giao điểm A của (C) và trục hoành. Khi đó, phương trình của đường thẳng d là
A.
B.
C.
D. .
Câu 22. Phương trình tiếp tuyến của đồ thị hàm số (C): tại giao điểm M của (C) với trục tung là
A.
B. .
C.
D. .
Câu 23. Cho hàm số có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số góc nhỏ nhất có phương trình là
A.
B.
C.
D. .
Câu 24. Cho hàm số có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số góc lớn nhất có phương trình là
A.
B. .
C. .
D. .
Câu 25. Cho hàm số có đồ thị (C). Tiếp tuyến của (C) tạo với trục hoành góc có phương trình là
A.
B. .
C.
D. .
Câu 26. Cho hàm số , m là tham số. Kí hiệu là đồ thị hàm số (1) và K là điểm thuộc , có hoành độ bằng -1. Tập tất cả các giá trị của tham số m để tiếp tuyến của tại điểm K song song với đường thẳng là
A. .
B.
C.
D. .
Câu 27. Cho hàm số có đồ thị (C). Từ điểm có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?
A. 0.
B. 3.
C. 2.
D. 1.
Câu 28. Cho hàm số có đồ thị (C). Tiếp tuyến tại điểm N của (C) cắt đồ thị (C) tại điểm thứ hai là . Khi đó tọa độ điểm N là
A. .
B. .
C. .
D. .
Câu 29. Cho hàm số có đồ thị (C) và gốc tọa độ O. Gọi là tiếp tuyến của (C), biết cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân. Phương trình là
A.
B.
C.
D. .
Câu 30. Cho hàm số có đồ thị (C). Tiếp tuyến của đồ thị (C) cắt các trục Ox, Oy lần lượt tại hai điểm A, B sao cho OB = 36OA có phương trình là:
A.
B. .
C.
D. .
Câu 31. Cho hàm số có đồ thị là . Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng bằng 2.
A. 2.
B. 3.
C. 4.
D. 0.
Câu 32. Cho hàm số có đồ thị là (C). Gọi I là giao điểm hai tiệm cận của (C). Tìm điểm M thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI?
A.
B.
C. .
D. .
Câu 33. Cho hàm số có đồ thị là (C) , đường thẳng . Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A,B. Gọi lần lượt là hệ số góc của các tiếp tuyến với (C) tại A,B. Tìm M để tổng đạt giá trị lớn nhất.
A. -1
B. -2
C. 3
D. -5
Câu 34. Cho hàm số .Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A,B và tam giác OAB cân tại gốc tọa độ O.
A.
B.
C.
D.
Câu 35. Cho hàm số có đồ thị (C). Lập phương trình tiếp tuyến của đồ thị (C) sao cho tiếp tuyến này cắt các trục Ox,Oy lần lượt tại các điểm A và B thoả mãn .
A.
B. .
C.
D. .
Câu 36. Cho hàm số có đồ thị (C). Biết khoảng cách từ đến tiếp tuyến của (C) tại M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất?
A. 3e
B. 2e
C. e
D. 4e
Câu 37. Cho hàm số có đồ thị (C). Biết tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) tại A, B sao cho AB ngắn nhất. Khi đó, độ dài lớn nhất của vectơ gần giá trị nào nhất ?
A. 7.
B. 5.
C. 6.
D. 4.
Câu 38. Cho hàm số có đồ thị (C). Phương trình tiếp tuyến của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị (C) đến bằng?
A. .
B. .
C.
D. .
Câu 39. Cho hàm số có đồ thị (C). Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến gần giá trị nào nhất?
A. 6.
B. 4.
C. 3.
D. 5.
Câu 40. Cho hàm số có đồ thị (C). Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến của (C) tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào?
A.
B.
C.
D. .
Đáp án
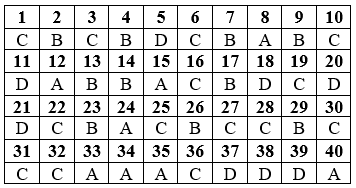
Xem thêm các dạng bài tập Toán lớp 12 có đáp án và lời giải chi tiết khác:
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12
