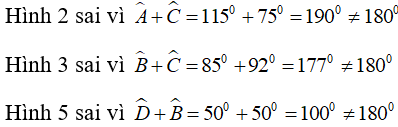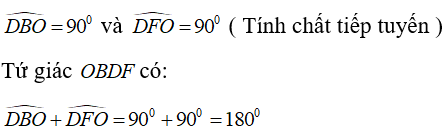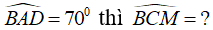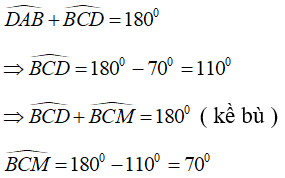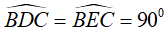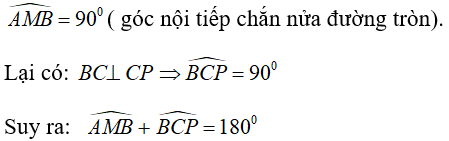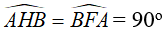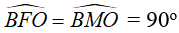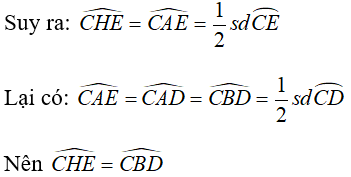Chuyên đề Tứ giác nội tiếp (2022) - Toán 9

Chuyên đề Tứ giác nội tiếp - Toán 9

A. Lý thuyết

1. Khái niệm về tứ giác nội tiếp

Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

Ví dụ 1. Bốn điểm A, B, C, D cùng nằm trên đường tròn (O) như hình vẽ.

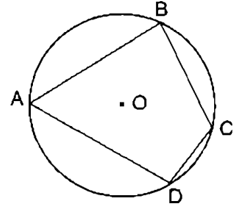
Do đó, ta gọi tứ giác ABCD là tứ giác nội tiếp.

Ví dụ 2. Bốn điểm M, N, P, Q không cùng nằm trên đường tròn (I) như hình vẽ.

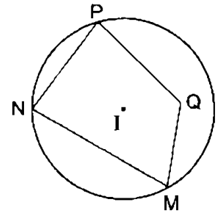
Do đó, ta gọi tứ giác MNPQ không là tứ giác nội tiếp.

2. Định lí

Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.

Ví dụ 3. Cho tứ giác ABCD nội tiếp đường tròn (O). Chứng minh $\widehat{BAD}+\widehat{BCD}={180}^o$.

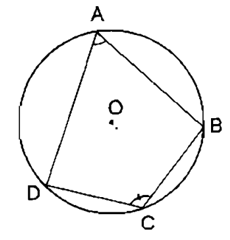
Lời giải:

Theo tính chất góc nội tiếp chắn cung, ta có:

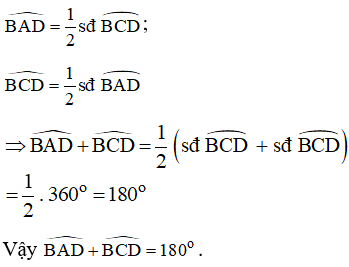
3. Định lí đảo

Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.

Ví dụ 4. Cho tứ giác ABCD có $\widehat{A}={100}^o;\widehat{C}={80}^o$.

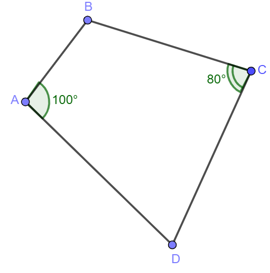
Khi đó, tứ giác ABCD có $\widehat{A}+\widehat{C}={100}^o+{80}^o={180}^o$.

Do đó tứ giác ABCD nội tiếp đường tròn.

4. Dấu hiệu nhận biết tứ giác nội tiếp

- Tứ giác có tổng hai góc đối bằng 180°.

- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

- Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.

- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.

- Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.

Ví dụ 5. Tứ giác ABCD có , góc ngoài của tam giác tại đỉnh A có số đo bằng 80^o.

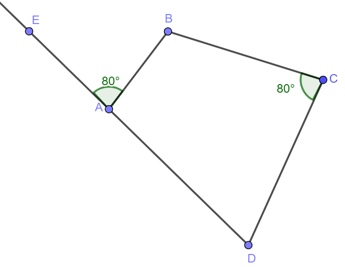
Xét tứ giác ABCD có:

+ $\widehat{A}$ và $\widehat{C}$ là hai góc đối diện.

+ Góc ngoài đỉnh A và góc trong đỉnh C có tổng số đo bằng 180^o.

Do đó tứ giác ABCD nội tiếp đường tròn.

B. Bài tập

I. Bài tập trắc nghiệm

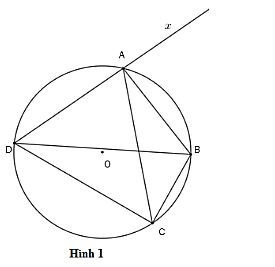
Câu 1: Cho tứ giác ABCD nội tiếp đường tròn (O) (hình 1) . Chọn khẳng định sai?

Lời giải:

(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )

Phương án A, B, C đúng

Chọn đáp án D

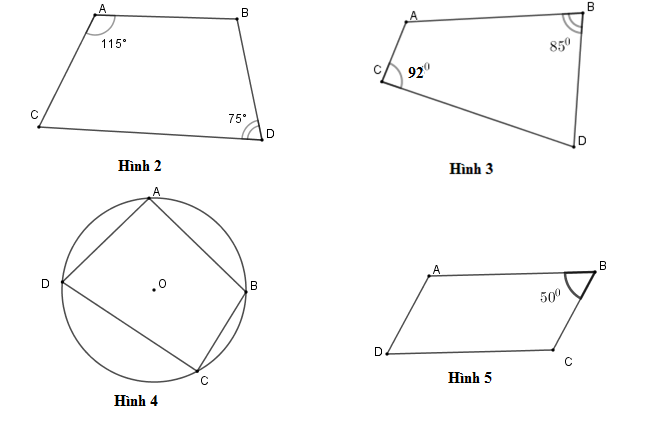
Câu 2: Tứ giác ở hình nào dưới đây là tứ giác nội tiếp?

A. Hình 2

B. Hình 3

C. Hình 4

D. Hình 5

Lời giải:

Hình 4 đúng vì tứ giác này có 4 đỉnh cùng thuộc một đường tròn

Chọn đáp án C

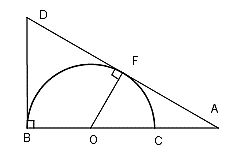
Câu 3: Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF.Bx của nửa kia đường tròn (O) ( với F là tiếp điểm ). Tia AF cắt tia Bx của nửa đường tròn tại D. Khi đó tứ giác OBDF là :

A. Hình thang

B. Tứ giác nội tiếp

C. Hình thang cân

D. Hình bình hành

Lời giải:

Ta có:

Nên nội tiếp được trong một đường tròn

Chọn đáp án B

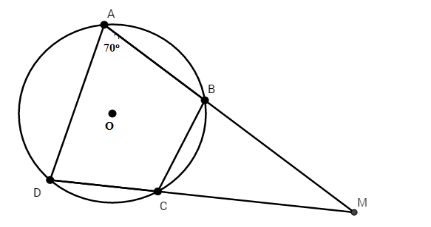
Câu 4: Tứ giác ABCD nội tiếp đường tròn có hai cạnh đối AB và CD cắt nhau tại M và 

A. 110°

B. 30°

C. 70°

D. 55°

Lời giải:

Tứ giác ABCD nội tiếp nên có :

Chọn đáp án C

Câu 5: Cho tam giác ABC có 2 đường cao BD và CE cắt nhau tại H. Tứ giác nào sau đây là tứ giác nội tiếp

A. AHBC

B. BCDE

C. BCDA

D. Không có tứ giác nội tiếp

Lời giải:

Ta có: BD và CE là đường cao của tam giác ABC nên 

Trên cùng 1 nửa mặt phẳng bờ BC, hai điểm D và E cùng nhìn đoạn thẳng BC dưới 1 góc vuông nên 4 điểm B, C, D, E cùng thuộc 1 đường tròn hay tứ giác BCDE là tứ giác nội tiếp .

Chọn đáp án B.

Câu 6: Cho đường tròn (O) có AB là đường kính. Trên đường thẳng AB lấy điểm C nằm ngoài đường tròn. Lấy điểm M bất kì nằm trên đường tròn (O). Gọi P là giao điểm của MB và đường vuông góc với AB tại Chọn khẳng định đúng .

A. Tứ giác PMAC là tứ giác nội tiếp

B. Tam giác BCM vuông

C. Tam giác BCP có CM là đường trung tuyến.

D. Tất cả sai

Lời giải:

Ta có:

Do đó, tứ giác PMAC là tứ giác nội tiếp

Chọn đáp án A.

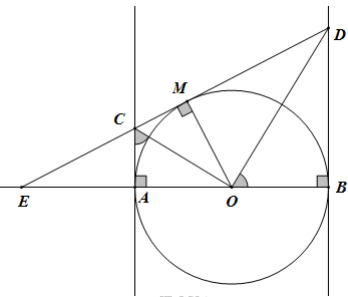
Câu 7: Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E (khác với điểm A). Tiếp tuyến kẻ từ điểm E cắt các tiếp tuyến kẻ từ điểm A và B của nửa đường tròn (O) lần lượt tại C và D. Gọi M là tiếp điểm của tiếp tuyến kẻ từ điểm E. Tìm khẳng định sai

A. Tứ giác OACM là tứ giác nội tiếp.

B. Tứ giác OBDM là tứ giác nội tiếp

C. Tứ giác ACDB là hình thang vuông

D. Tứ giác ACDO là tứ giác nội tiếp

Lời giải:

Suy ra OMDB là tứ giác nội tiếp.

Chọn đáp án D.

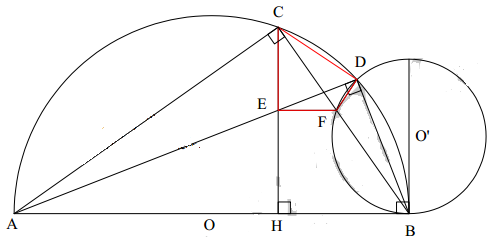
Câu 8: Cho nửa đường tròn (O) đường kính AB, trên nửa đường tròn lấy điểm C (C không trùng với A, B). Gọi H là hình chiếu của C trên đường thẳng AB. Trên cung CB lấy điểm D (D khác C, B), Hai đường thẳng AD và CH cắt nhau tại E. . Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B. Đường tròn (O’) cắt CB tại F khác B.

Chọn khẳng định sai ?

A. Tứ giác BDEH nội tiếp

B. AC² = AE.AD

C. EF // AB.

D. Có 2 phương án sai .

Lời giải:

* Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B.

Đường tròn (O’) cắt CB tại F khác B. Chứng minh EF // AB.

Ta có:

Hai góc ở vị trí đồng vị ⇒ EF//AB

Chọn đáp án D.

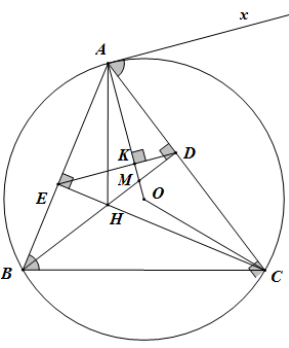
Câu 9: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là giao điểm hai đường cao BD và CE của tam giác ABC (D ∈ AC, E ∈ AB). ) Đường thẳng AO cắt ED và BD lần lượt tại K và M. Tìm khẳng định đúng nhất?

A. Tứ giác ADHE nội tiếp trong một đường tròn.

B. AK.AM = AD²

C. 

D.Tất cả đúng

Lời giải:

* Chứng minh tứ giác ADHE nội tiếp trong một đường tròn.

Trong nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia tiếp tuyến Ax với đường tròn (O)

Chọn đáp án D.

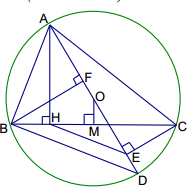
Câu 10: Cho tam giác ABC (AB < AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC.

Tìm khẳng định sai ?

A. Tứ giác ABHF nội tiếp

B. Tứ giác BMFO nội tiếp.

C. HE // BD

D. Có ít nhất một khẳng định sai

Lời giải:

* Chứng minh các tứ giác ABHF và BMFO nội tiếp.

- Từ giả thiết suy ra: 

=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)

Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB

- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC

Khi đó: 

Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).

Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB

* Chứng minh HE // BD.

Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.

Và chúng ở vị trí so le trong suy ra: HE // BD

Chọn đáp án D.

II. Bài tập tự luận có lời giải

Câu 1:  Cho tứ giác ABCD nội tiếp đường tròn (O). M là điểm chính giữa cung AB. Nối M với D, M với C cắt AB lần lượt ở E và F. Chứng minh tứ giác PEDC là tứ giác nội tiếp.

Lời giải:

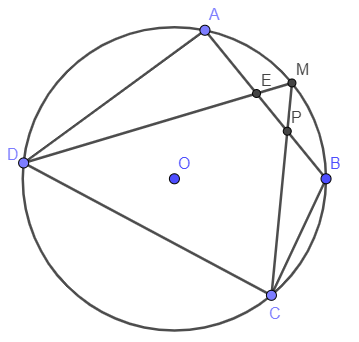
Ta có:

$\widehat{MDC}$ là góc nội tiếp chắn cung $\stackrel{⏜}{MC}$

 $\Rightarrow \widehat{MDC}=\frac{1}{2}$sđ $\stackrel{⏜}{MC}$  (định lí)

Mà $\stackrel{⏜}{MC}=\stackrel{⏜}{MB}+\stackrel{⏜}{BC}$

Nên $\Rightarrow \widehat{MDC}=\frac{1}{2}$ (sđ $\stackrel{⏜}{MB}$ + sđ $\stackrel{⏜}{BC}$ ) (1)

Lại có $\widehat{CPB}$ là góc có đỉnh nằm bên trong đường tròn

$\Rightarrow \widehat{CPB}=\frac{1}{2}$(sđ $\stackrel{⏜}{BC}$  + sđ $\stackrel{⏜}{MA}$ )  (2)

Lạ có M là điểm chính giữa cung AB

sđ $\stackrel{⏜}{MA}$ = sđ $\stackrel{⏜}{MB}$  (định lý) (3)

Từ (1); (2); (3) $\Rightarrow \widehat{CPB}=\widehat{MDC}$

Xét tứ giác PEDC có:

Mà góc $\widehat{CPB}$ là góc ngoài của đỉnh P và đỉnh P và D là hai đỉnh đối diện nhau

Do đó: tứ giác PEDC là tứ giác nội tiếp (dấu hiệu nhận biết).

Câu 2: Cho tam gác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Lời giải:

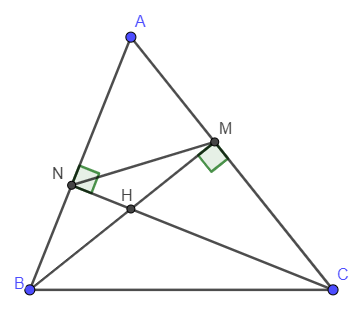
Vì BM là đường cao của tam giác ABC nên $\widehat{AMB}=\widehat{BMC}=90°$

Vì CN là đường cao của tam giác ABC nên $\widehat{ANC}=\widehat{BNC}=90°$

Xét tứ giác AMHN có:

$\widehat{AMB}+\widehat{ANC}=90°+90°=180°$

Mà góc $\widehat{AMB}$ và $\widehat{ANC}$ là hai góc đối nhau

Do đó tứ giác AMHN là tứ giác nội tiếp (dấu hiệu nhận biết).

Xét tứ giác BNMC có:

$\widehat{BMC}=\widehat{BNC}=90°$

Mà hai góc này là hai góc có đỉnh kề nhau và cùng nhìn cạnh BC dưới một góc $90°$

Do đó tứ giác BNMC là tứ giác nội tiếp.

Câu 3: Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm của đường tròn đó.

Lời giải:

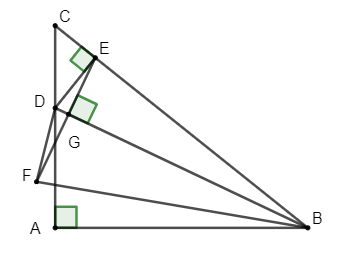
Vì E là hình chiếu của D lên BC nên $DE\perp BC$$\Rightarrow \widehat{DEB}=90°$

Gọi O là trung điểm của BD.

Xét tam giác DEB vuông tại E, trung tuyến EO ta có:

OE = OD = OB = $\frac{1}{2}$ BD (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (1)

Xét tam giác ABD vuông tại A, trung tuyến AO ta có:

AO = OD = OB = $\frac{1}{2}$BD (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (1)

Vì E đối xứng với F qua BD nên $E\text{}F\perp BD$ . Gọi giao điểm của EF với BD là G.

Vì E đối xứng với F qua BD nên EG = GF.

Xét tam giác DGF và tam giác DGE có:

GF = GE

DG chung

$\widehat{DGF}=\widehat{DGE}=90°$

Do đó $\Delta DGF=\Delta DGE$ (c – g – c)

$\Rightarrow \left\{\begin{array}{l}DF=DE\\ \widehat{FDG}=\widehat{EDG}\end{array}\right.$(các cặp cạnh tương ứng và các cặp góc tương ứng)

Xét FDB và tam giác EDB có:

BD chung

DF = DE (chứng minh trên)

$\widehat{FDG}=\widehat{EDG}$ (chứng minh trên)

Do đó $\Delta FDB=\Delta EDB$  (c – g – c)

$\Rightarrow \widehat{DFB}=\widehat{DEB}=90°$

Xét tam giác FDB vuông tại F, trung tuyến FO ta có:

FO = OD = OB = $\frac{1}{2}$ BD (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (3)

Từ (1); (2); (3) ta có:

OA = OB = OD = OE = OF = $\frac{1}{2}$ BC

Do đó 5 điểm A, B, D, E, F cách đều O. Do đó O là tâm đường tròn ngoại tiếp đi qau 5 điểm A, B, D, E, F.

Câu 4: Từ điểm S nằm ở ngoài đường tròn (O) kẻ tiếp tuyến SA; SB với A, B là tiếp điểm và cát tuyến SCD với đường tròn. Gọi I là trung điểm của CD. Chứng minh 5 điểm A, I, O, B, S cùng thuộc một đường tròn.

Lời giải:

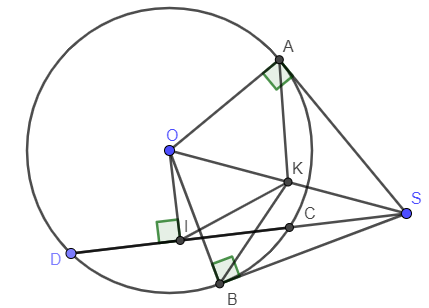
Vì SA là tiếp tuyến của đường tròn, A là tiếp điểm nên SA vuông góc với OA.

$\Rightarrow \widehat{SAO}=90°$

Vì SB là tiếp tuyến của đường tròn, B là tiếp điểm nên SB vuông góc với OB.

$\Rightarrow \widehat{SBO}=90°$

Vì I là trung điểm của CD nên OI vuông góc với CD (tính chất)

$\Rightarrow \widehat{SOI}=90°$

Gọi trung điểm của SO là K.

Tam giác OAS vuông tại A với K là trung điểm của SO

$\Rightarrow OK=KS=AK=\frac{1}{2}SO$ (định lí đường trung tuyến ứng với cạnh huyền)   (1)

Tam giác OBS vuông tại B với K là trung điểm của SO

$\Rightarrow OK=KS=BK=\frac{1}{2}SO$ (định lý đường trung tuyến ứng với cạnh huyền)   (2)

Tam giác OIS vuông tại I có K là trung điểm của SO

$\Rightarrow OK=KS=IK=\frac{1}{2}SO$ (định lí đường trung tuyến ứng với cạnh huyền)   (3)

Từ (1); (2); (3) $\Rightarrow OK=KS=IK=AK=BK=\frac{1}{2}SO$

Hay 5 điểm A, B, S, I, O cách đều điểm K.

Vậy 5 điểm A, B, S, I, O cùng nằm trên một đường tròn (K) bán kính KS.

Câu 5: Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F. Chứng minh:

a) Tứ giác AHCK là tứ giác nội tiếp.

b) $AH.AB=A{D}^2$

c) Tam giác ACF là tam giác cân.

Lời giải:

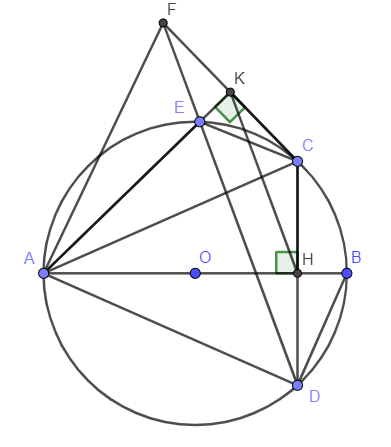
a) Vì CD vuông góc với AB tại H $\Rightarrow \widehat{CHA}=90°$

Vì CK vuông góc với AE tại K $\Rightarrow \widehat{AKC}=90°$

Xét tứ giác AKCH có:

$\widehat{AKC}+\widehat{CHA}=90°+90°=180°$

Mà hai góc này ở vị trí đối nhau

Do đó tứ giác AKCH là tứ giác nội tiếp.

b) Vì AB là đường kính do đó $\widehat{ADB}$ là góc nội tiếp chắn nửa đường tròn

$\Rightarrow \widehat{ADB}=90°$

Xét tam giác ABD vuông tại D, đường cao DH ta có:

$AH.AB=A{D}^2$ (hệ thức lượng trong tam giác vuông)

c) Vì AHCK là tứ giác nối tiếp

$\Rightarrow \widehat{KHC}=\widehat{KAC}$ (hai góc có đỉnh kề nhau cùng nhìn cạnh KC)

Lại có $\widehat{KAC}=\widehat{EDC}$ (hai góc nội tiếp cùng chắn cung $\stackrel{⏜}{EC}$)

Do đó: $\widehat{EDC}=\widehat{KHC}$

Mà hai góc này ở vị trí đồng vị với nhau

Do đó KH // DF

Mặt khác AB vuông góc với CD tại H nên H là trung điểm của CD (tính chất)

Vì H là trung điểm của CD, KH // DF do đó K là trung điểm của CF (tính chất)

Xét tam giác ACF có:

AK vuông góc với CF

K là trung điểm của CF

Do đó AK vừa là đường cao vừa là đường trung tuyến của tam giác ACF

=> Tam giác ACF là tam giác cân tại A.

Câu 6: Cho nửa (O) đường kính AB. Lấy M thuộc OA (M không trùng với O và A). Qua M kẻ đường thẳng d vuông góc với AB. Trên d lấy N sao cho ON > R. Nối NB cắt (O) tại C. Kẻ tiếp tuyến NE với (O) (E là tiếp điểm, A và E thuộc cùng nửa mặt phẳng bờ d. Chứng minh:

a) Tứ giác O, E, M, N thuộc cùng một đường tròn.

b) $N{E}^2=NC.NB$

c) $\widehat{NEH}=\widehat{NME}$ (H là giao điểm của AC và d).

Lời giải:

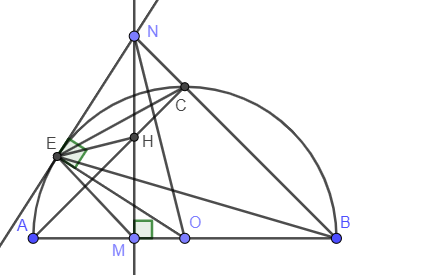
a) Vì NE là tiếp tuyến (O) nên OE vuông góc với EN

$\Rightarrow \widehat{OEN}=90°$

Vì MN vuông góc với AB nên $\widehat{NMO}=90°$

 Xét tứ giác ENOM có:

$\widehat{OEN}=\widehat{NMO}=90°$

Mà hai góc này có đỉnh kề nhau cùng nhìn cạnh ON

Do đó tứ giác ENOM là tứ giác nội tiếp

=> bốn điểm E, N, O, M cùng thuộc một đường tròn.

b) Ta có: $\widehat{NBE}$ là góc nội tiếp chắn cung $\stackrel{⏜}{NC}$

$\widehat{NEC}$ là góc nội tiếp chắn cung $\stackrel{⏜}{NC}$

Do đó $\widehat{NBE}=\widehat{NEC}$

 Xét tam giác NEC và tam giác NBE có:

$\widehat{N}$ chung

$\widehat{NEC}=\widehat{NBE}$

Do đó: $\Delta NEC\backsim \Delta NBE$  (g – g)

$\Rightarrow \frac{NE}{NB}=\frac{NC}{NE}$ (hai cặp cạnh tương ứng)

Hay $N{E}^2=NB.NC$

c) Vì $\widehat{ACB}$ là góc nội tiếp chắn nửa đường tròn $\Rightarrow \widehat{ACB}=90°$

$\Rightarrow \widehat{NCH}=90°$

Xét tam giác HCN và tam giác BMN có:

$\widehat{NCH}=\widehat{NMB}=90°$

$\widehat{N}$ chung

Do đó $\Delta HCN\backsim \Delta BMN$ (g – g)

$\Rightarrow \frac{NC}{NM}=\frac{NH}{NB}$ (hai cạnh tương ứng)

$\Rightarrow NC.NB=NM.NH$

Theo cấu b ta có: $NC.NB=N{E}^2$

Do đó: $N{E}^2=NM.NH$

$\Rightarrow \frac{NE}{NM}=\frac{NH}{NE}$

Xét hai tam giác NEH và tam giác NME có:

$\widehat{N}$ chung

$\frac{NE}{NM}=\frac{NH}{NE}$

Do đó $\Delta NEH\backsim \Delta NME$ (c – g – c)

$\Rightarrow \widehat{NEH}=\widehat{NME}$(hai góc tương ứng).

Câu 7: Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Lời giải:

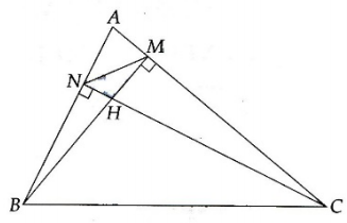
$\widehat{BMC}$ và $\widehat{BNC}$ cùng nhìn cạnh BC dưới một góc 90^o.

Do đó tứ giác BNMC là tứ giác nội tiếp.

Vậy các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Câu 8: Cho đường tròn (O) đường kính AB. Lấy điểm M thuộc đoạn thẳng OA, điểm N thuộc đường tròn (O). Từ A và B vẽ các tiếp tuyến Ax và By. Đường thẳng qua C và vuông góc với NM cắt Ax, By theo thứ tự tại C và D.

a) Chứng minh ACNM và BDNM là các tứ giác nội tiếp đường tròn.

b) Chứng minh ∆ANB đồng dạng với ∆CMD.

Lời giải:

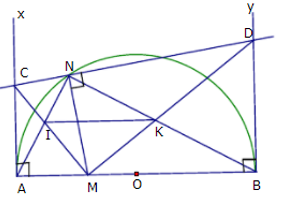
a) Xét tứ giác ACNM có:

$\widehat{MNC}={90}^o$ (vì $NM\perp CD$);

$\widehat{MAC}={90}^o$ (vì Ax là tiếp tuyến của nửa đường tròn (O)).

Do đó tứ giác ACNM nội tiếp đường tròn đường kính MC.

Xét tứ giác BDNM có:

$\widehat{MND}={90}^o$ (vì $NM\perp CD$);

$\widehat{MBD}={90}^o$ (vì By là tiếp tuyến của nửa đường tròn (O)).

Do đó tứ giác BDNM nội tiếp đường tròn đường kính MD.

Vậy các tứ giác ACNM và BDNM là các tứ giác nội tiếp đường tròn.

b) Xét ∆ANB và ∆CMD có:

$\widehat{BAN}=\widehat{DCM}$ (tứ giác ACNM nội tiếp)

$\widehat{ABN}=\widehat{CDM}$ (tứ giác BDNM nội tiếp)

Do đó ∆ANB  ∆CMD (g.g).

Câu 9: Trên đường tâm O có một cung AB và S là điểm chính giữa của cung đó. Trên dây AB lấy hai điểm E và H. Các đường thẳng SH và SE cắt đường tròn theo thứ tự tại C và D. Chứng minh EHCD là một tứ giác nội tiếp.

Lời giải:

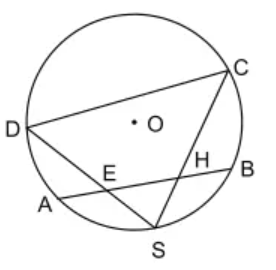
S là điểm chính giữa của cung nhỏ AB (gt)

 $\Rightarrow \stackrel{⏜}{SA}=\stackrel{⏜}{SB}$(1)

Ta lại có:

 (góc có đỉnh ở bên trong đường tròn) (2)

$\widehat{DCS}=\frac{1}{2}$sđ$\stackrel{⏜}{DAS}=\frac{1}{2}\left(sđ\stackrel{⏜}{\text{D}A}+sđ\stackrel{⏜}{SA}\right)$  (góc nội tiếp chắn cung) (3)

Từ (2) và (3) ta suy ra:  $\widehat{DEB}+\widehat{DCS}=\frac{1}{2}\left(sđ\stackrel{⏜}{\text{D}CB}+sđ\stackrel{⏜}{AS}+sđ\stackrel{⏜}{\text{D}A}+sđ\stackrel{⏜}{SA}\right)$(4)

Từ (1) và (4) ta suy ra:

$\widehat{DEB}+\widehat{DCS}=\frac{1}{2}\left(sđ\stackrel{⏜}{\text{D}CB}+sđ\stackrel{⏜}{BS}+sđ\stackrel{⏜}{\text{D}A}+sđ\stackrel{⏜}{SA}\right)=\frac{{360}^o}{2}={180}^o$

Hay $\widehat{DEH}+\widehat{DCH}={180}^o$

Vậy tứ giác EHCD là tứ giác nội tiếp.

Câu 10: Cho tam giác ABC. Các đường phân giác trong của góc B và góc C cắt nhau tại S, các đường phân giác ngoài của góc B và góc C cắt nhau tại E. Chứng minh BSCE là một tứ giác nội tiếp.

Lời giải:

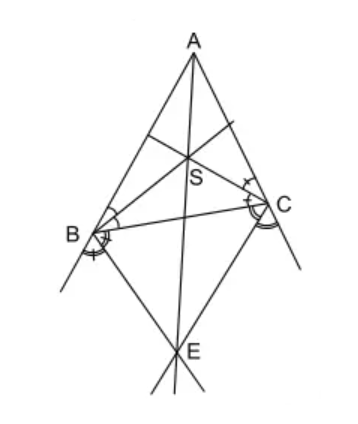
Ta có:

BS vuông góc với BE tại B (do hai tia phân giác của hai góc kề bù thì vuông góc với nhau)

$\Rightarrow \widehat{SBE}={90}^o$

 

CS vuông góc với CE tại C (do hai tia phân giác của hai góc kề bù thì vuông góc với nhau)

$\Rightarrow \widehat{SCE}={90}^o$

 

Xét tứ giác BSCE có: $\widehat{SBE}+\widehat{SCE}={90}^o+{90}^o={180}^o$

Do đó, BSCE là tứ giác nội tiếp.

III. Bài tập vận dụng

Câu 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ đường kính AC của đường tròn (O) cắt (O’) tại F. Kẻ đường kính AE của (O’) cắt đường tròn (O) tại G. Chứng minh:

a) Tứ giác GFEC nội tiếp;

b) GC, FE, AB đồng quy.

Câu 2: Cho điểm C nằm trên nửa đường tròn (O) với đường kính AB sao cho cung $\stackrel{⏜}{AC}$  lớn hơn cung $\stackrel{⏜}{BC}$  ($B\ne C$ ). Đường thẳng vuông góc với AB tại O cắt dây AC tại D. Chứng minh tứ giác BCDO nội tiếp.

Câu 3: Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kỳ (H không trùng O, B). Trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn; MA và MB thứ tự cắt đường (O) ở C và D. Gọi I là giao điểm của AD và BC. Chứng minh các tứ giác MCID và MCHB là tứ giác nội tiếp.

Câu 4: Cho điểm A nằm ngoài đường tròn (O), qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm). Chứng minh tứ giác ABOC là tứ giác nội tiếp.

Câu 5: Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm thuộc đường tròn. Vẽ MH vuông góc với BC tại H, vẽ MI vuông góc với AC. Chứng minh MIHC là tứ giác nội tiếp.

Câu 6: Cho đường tròn (O) đường kính AB. Gọi I là trung điểm của OA, dây CD vuông góc với AB tại I. Lấy K tùy ý trên cung BC nhỏ, AK cắt CD tại H.

a) Chứng minh: Tứ giác BIHK là tứ giác nội tiếp.

b) Chứng minh: AH.AK có giá trị không đổi khi K di chuyển trên cung nhỏ BC.

c) Kẻ DN vuông góc với CB, DM vuông góc với AC. Chứng minh đường thẳng MN, AB, CD đồng quy.

Câu 7: Cho tam giác ABC cân tại A. Đường thẳng xy song song với BC cắt AB tại E và cắt AC tại F. Chứng minh tứ giác EFCB nội tiếp.

Câu 8: Cho tam giác ABC nhọn. Đường tròn (O; R) có đường kính BC cắt AB, AC lần lượt tại F và E; BE cắt CF tại H.

a) Chứng minh tứ giá AFHE nội tiếp. Từ đó, xác định tâm I của đường tròn ngoại tiếp tứ giác này.

b) Tia AH cắt BC tại D. Chứng minh HE.HB = 2HD.HI

c) Chứng minh bốn điểm D, E, I, F cùng nằm trên một đường tròn.

Câu 9: Cho tam giác ABC vuông tại A và điểm M thuộc cạnh AC. Vẽ đường tròn tâm O đường kính MC cắt BC tại E. Nối BM cắt đường tròn (O) tại N, AN cắt đường tròn (O) tại D. Lấy I đối xứng với M qua A, K đối xứng với M qua E.

a) Chứng minh BANC là tứ giác nội tiếp.

b) Chứng minh CA là phân giác của $\widehat{BCD}$ .

c) Chứng minh ABED là hình thang.

Câu 10: Cho đường tròn (O; R) và điểm A cố định ngoài dường tròn. Qua A kẻ hai tiếp tuyến AM, AN tới đường tròn (M, N là hai tiếp điểm). Một đường thẳng d đi qua A cắt đường tròn (O; R) tại B và C (AB < AC). Gọi I là trung điểm của BC.

a) Chứng minh năm điểm A, M, N, O, I thuộc cùng một đường tròn.

b) Chứng minh: $A{M}^2=AB.AC$ .

c) Đường thẳng qua B, song song với AM cắt MN tại E. Chứng minh IE song song với MC.

d) Chứng minh khi d di chuyển quanh điểm A thì trọng tâm G của tam giác MBC luôn nằm cố định trên một đường thẳng.

Câu 11: Cho đường tròn (O; R) và dây CD cố định. Điểm M thuộc tia đối của tia CD. Qua M kẻ hai tếp tuyến MA và MB tới đường tròn, A, B là các tiếp điểm (A thuộc cung lớn CD). Gọi I là trung điểm của CD. Nối BI cắt đường tròn tại E (E khác B). Nối OM cắt AB tại H.

a) Chứng minh: AE // CD.

b) Tìm vị trí của M để AM vuông góc với MB.

Câu 12: Cho đường tròn (O; R), hai điểm C, D thuộc đường tròn, B là điểm chỉnh giữa của cung nhỏ CD. Kẻ đường kính BA; trên tia đối của tia AB lấy điểm S. Nối S với C cắt (O) tại M, MD cắt AB tại K, MB cắt AC tại H. Chứng minh:

a) Tứ giác AMHK nội tiếp

b) HK // CD.

Câu 13: Cho hình vuông ABCD. E di động trên đoạn CD (E khác C, D). Tia AE cắt đường thẳng BC tại F, Ax vuông góc với AE tại A cắt đường thẳng DC tại K. Chứng minh:

a) $\widehat{CAF}=\widehat{CKF}$

b) Tam giác KAF vuông cân.

c) Đường thẳng BD đi qua trung điểm I của KF.

d) Tứ giác IMCF nội tiếp với M là giao điểm của BD và AE.

Câu 14: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O), M là điểm thuộc cung nhỏ AC. Vẽ MH vuông góc với BC tại H, MI vuông góc với AC tại I.

a) Chứng minh: $\widehat{IHM}=\widehat{ICM}$ .

b) Đường thẳng HI cắt đường thẳng AB tại K. Chứng minh MK vuông góc với BK.

c) Chứng minh tam giác MIH đồng dạng với tam giác MAB.

d) Gọi E là trung điểm của IH và F là trung điểm của AB. Chứng minh tứ giác KMEF nội tiếp từ đó suy ra ME vuông góc với EF

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Đường tròn ngoại tiếp. Đường tròn nội tiếp

Chuyên đề Độ dài đường tròn, cung tròn

Chuyên đề Diện tích hình tròn, hình quạt tròn

Chuyên đề Ôn tập chương III

Chuyên đề Hình trụ - Diện tích xung quanh và thể tích của hình trụ