Nội dung bài viết

    Xem thêm

    Chuyên đề Hệ thức lượng trong tam giác vuông mới nhất - Toán 9

    Với Chuyên đề Toán 9 Chương 1: Hệ thức lượng trong tam giác vuông mới nhất được biên soạn bám sát chương trình Toán lớp 9 giúp bạn học tốt môn Toán hơn.

    1 734 lượt xem
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Chuyên đề Toán 9 Chương 1: Hệ thức lượng trong tam giác vuông

    Chuyên đề Một số hệ thức về cạnh và đường cao trong tam giác vuông

    Xem chi tiết

    Chuyên đề Tỉ số lượng giác của góc nhọn

    Xem chi tiết

    Chuyên đề Một số hệ thức về cạnh và góc trong tam giác vuông

    Xem chi tiết

    Chuyên đề Ứng dụng thực tế các tỉ số lượng giác của góc nhọn

    Xem chi tiết

    Chuyên đề Ôn tập chương 1

    Xem chi tiết

    Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

    Chương 2: Đường tròn

    Chương 3: Hệ hai phương trình bậc nhất hai ẩn

    Chương 4: Hàm số y = ax^2 (a khác 0). Phương trình bậc hai một ẩn

    Chương 3: Góc với đường tròn

    Chương 4: Hình Trụ - Hình Nón - Hình Cầu

    ------------------------------------------------------------

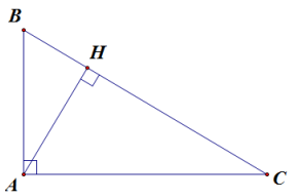
    Chuyên đề Một số hệ thức về cạnh và đường cao trong tam giác vuông - Toán 9

    A. Lý thuyết

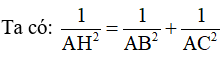
    1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyềnĐịnh lí 1. Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.Ví dụ 1. Tam giác ABC vuông tại A, đường cao AH.Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)
    Ta có: AB2 = BC . BH; AC2 = BC . HC.2. Một số hệ thức liên quan tới đường caoĐịnh lí 2. Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.Ví dụ 2. Tam giác ABC vuông tại A, đường cao AH.Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)
    Ta có: AH2 = BH . HC.Định lí 3. Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.Ví dụ 3. Tam giác ABC vuông tại A, đường cao AH.Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)
    Ta có: AB . AC = BC . AH.Định lí 4. Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.Ví dụ 4. Tam giác ABC vuông tại A, đường cao AH.Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)Lý thuyết Một số hệ thức về cạnh và đường cao trong tam giác vuông chi tiết – Toán lớp 9 (ảnh 1)

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 734 lượt xem
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: