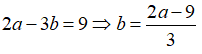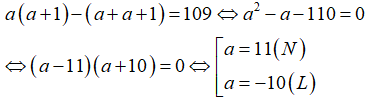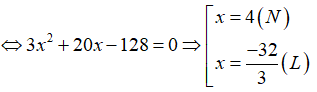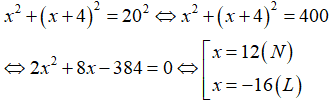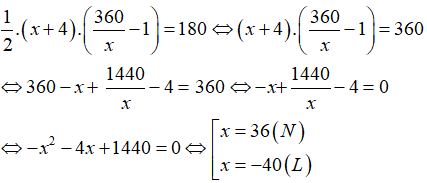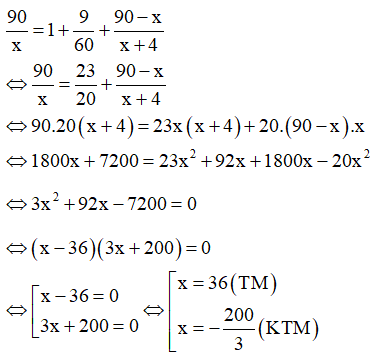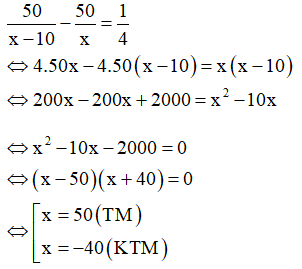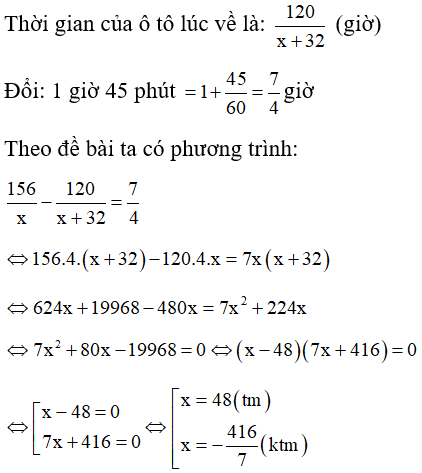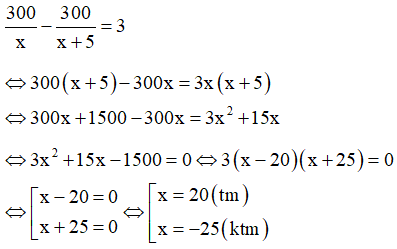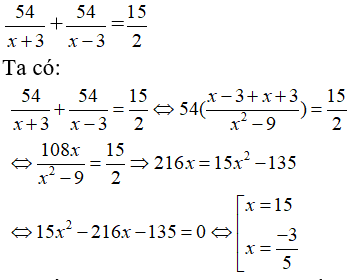Chuyên đề Giải bài toán bằng cách lập phương trình (2022) - Toán 9

Chuyên đề Giải bài toán bằng cách lập phương trình - Toán 9

A. Lý thuyết

Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

- Chọn ẩn và đặt điều kiện thích hợp cho chúng

- Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải phương trình nói trên. 

Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện và kết luận.

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Cho hai số tự nhiên biết rằng hai lần số thứ nhất hơn ba lần số thứ hai là 9 và hiệu các bình phương của chúng bằng 119. Tìm số lớn hơn.

A. 12

B. 13

C. 32

D. 33

Lời giải:

Gọi số thứ nhất là a; a ∈ N , số thứ hai là b; b ∈ N

Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:

Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:

a² – b² = 119 hay

Chọn đáp án A.

Câu 2: Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109. Tìm số bé hơn.

A. 12

B. 13

C. 32

D. 11

Lời giải:

Gọi số bé hơn là a; a ∈ N thì số lớn hơn là a + 1

Vì tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109 nên ta có phương trình:

Vậy số bé hơn là 11.

Chọn đáp án D.

Câu 3: Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm 5cm thì được một hình chữ nhật mới có diện tích bằng 153 cm². Tìm chu vi hình chữ nhật ban đầu.

A. 16

B. 32

C. 34

D. 36

Lời giải:

Gọi x là chiều rộng hình chữ nhật lúc đầu (x > 0) (cm)

Chiều dài hình chữ nhật lúc đầu: 3x (cm)

Chiều rộng hình chữ nhật lúc sau: x + 5 (cm)

Chiều dài hình chữ nhật lúc sau: 3x + 5 (cm)

Theo đề bài ta có phương trình: (x + 5)(3x + 5) = 153

Vậy chiều dài và chiều rộng hình chữ nhật ban đầu là: 12 cm và 4 cm

Suy ra chu vi hình chữ nhật ban đầu là: (12 + 4).2 = 32 (cm)

Chọn đáp án B.

Câu 4: Cho tam giác vuông có cạnh huyền bằng 20 cm. Hai cạnh góc vuông có độ dài hơn kém nhau 4 cm. Một trong hai cạnh góc vuông của tam giác vuông có độ dài là:

A. 16

B. 15

C. 14

D. 13

Lời giải:

Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)

Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4

Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:

Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Chọn đáp án A.

Câu 5: Một thửa ruộng hình tam giác có diện tích 180 cm². Tính chiều dài cạnh đáy thửa ruộng, biết rằng nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm đi 1m thì diện tích không đổi.

A. 10

B. 35

C. 36

D. 18

Lời giải:

Gọi độ dài cạnh đáy là x (cm) (x > 0)

Chiều cao của thửa ruộng có độ dài là: 360/x (cm)

Vì nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm 1m đi thì diện tích không đổi nên ta có phương trình:

Vậy chiều dài cạnh đáy của thửa ruộng có độ dài là: 36 cm

Chọn đáp án C.

Câu 6: Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90 km trong một thời gian đã định. Sau khi đi được 1 giờ, ngườ đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng hẹn, người ấy phải tăng vận tốc thêm 4 km/h. Tính vận tốc lúc đầu của người đó.

A. 36 km / h

B. 40 km/ h

C. 45km/ h

D. 50km/ h

Lời giải:

Gọi vận tốc ban đầu của người đó là x (km/h) (x > 0).

Thời giạn dự định người đó đi hết quãng đường là 90/x (h).

Quãng đường người đó đi được sau 1 giờ là x (km).

Quãng đường còn lại người đó phải tăng tốc là 90 – x (km).

Vận tốc của người đó sau khi tăng tốc là x + 4 (km/h).

Thời gian người đó đi hết quãng đường còn lại là 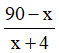 (h).

Theo đề bài ta có phương trình:

Vậy vận tốc lúc đầu của người đó là 36 km/h.

Chọn đáp án A.

Câu 7: Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến

B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc mỗi xe.

A. 40 và 30

B. 40 và 50

C. 50 và 60

D. 45 và 55

Lời giải:

Gọi vận tốc của xe thứ nhất là x (km/h) (x > 10).

Vận tốc của xe thứ hai là x – 10 (km/h).

Thời gian xe thứ nhất đi từ A đến B là 50/x (h).

Thời gian xe thứ hai đi từ A đến B là 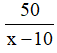 (h).

Vì xe thứ nhất đến B trước xe thứ hai 15 phút = 1/4 h nên ta có phương trình:

Vậy vận tốc của xe thứ nhất là 50 km/h, vận tốc của xe thứ hai là 40 km/h.

Chọn đáp án B.

Câu 8: Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36km so với lúc đi và vận tốc tăng so với lúc đi là 32km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.

A. 36 km/ h

B. 40km/h

C. 45km/ h

D. 48 km/ h

Lời giải:

Gọi vận tốc của ô tô khi đi từ A đến B là x (km/h) (x > 0)

Thời gian ô tô đi từ A đến B là: 156/x (giờ)

Vận tốc của ô tô lúc về là: x + 32 (km) .

Vậy vận tốc của ô tô lúc đi từ A đến B là 48km/h

Chọn đáp án D.

Câu 9: Để phục vụ cho Festival Huế 2018, một cơ sở sản xuất nón lá dự kiến làm ra 300 chiếc nón lá trong một thời gian đã định. Do được bổ sung thêm nhân công nên mỗi ngày cơ sở đó làm ra được nhiều hơn 5 chiếc nón lá so với dự kiến ban đầu, vì vậy cơ sở sản xuất đã hoàn thành 300 chiếc nón lá sớm hơn 3 ngày so với thời gian đã định. Hỏi theo dự kiến ban đầu, mỗi ngày cơ sở đó làm được ra bao nhiêu chiếc nón lá? Biết rằng số chiếc nón lá làm ra mỗi ngày là bằng nhau và nguyên chiếc.

A. 10

B. 15

C. 20

D. 25

Lời giải:

Gọi số chiếc nón lá mỗi ngày cơ sở đó làm được là x (chiếc)

Số ngày cơ sở đó dự kiến làm hết 300 chiếc nón lá là: 300/x (ngày)

Sau khi làm tăng thêm 5 chiếc nón lá một ngày thì thời gian cơ sở đó làm hết 300 chiếc nón lá là: 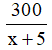 (ngày).

Theo đề bài ta có phương trình:

Vậy theo dự kiến, mỗi ngày cơ sở đó làm được 20 chiếc nón lá.

Chọn đáp án C.

Câu 10: Một ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút. Tính vận tốc thực của ca nô biết quãng đường sông AB dài 54 km và vận tốc dòng nước là 3 km/h.

Lời giải:

Đổi 7 giờ 30 phút= 15/2 (h)

Gọi vận tốc thực của ca nô là x (km/h; x > 3).

vận tốc của ca nô khi xuôi dòng sông từ A đến B là: x + 3 (km/h)

Vận tốc của ca nô khi ngược dòng sông từ B về A là: x – 3 (km/h)

Thời gian của ca nô khi xuôi dòng sông từ A đến B là: 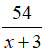 (h)

Thời gian của ca nô khi ngược dòng sông từ B về A là: 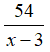 (h)

Do ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:

Ta thấy chỉ có x = 15 thỏa mãn điều kiện x > 3.

Vậy vận tốc thực của ca nô là 15 (km/h).

II. Bài tập tự luận có lời giải

Câu 1: Khoảng cách giữa hai bến sông A và B là 60km. Một xuồng máy đi xuôi dòng từ A đến B, nghỉ 30 phút tại B rồi quay trở lại đi ngược dòng 25km để đến bến C. Thời gian kể từ lúc đi đến lúc quay trở lại bến C hết tất cả 8 giờ. Tính vận tốc xuồng máy khi nước yên lặng biết rằng vận tốc nước chảy là 1km/h.

Lời giải:

+ Gọi x (km/h) là vận tốc của xuồng khi nước yên lặng. Điều kiện x > 1.

+ Thời gian xuồng máy đi từ A đến B là: $\frac{60}{\mathrm{x}+1}\left(\mathrm{h}\right)$

+ Thởi gian xuồng ngược dòng từ B về C là: $\frac{25}{\mathrm{x}-1}\left(\mathrm{h}\right)$.

Vì tổng thời gian cả đi xuôi dòng và ngược dòng là 8h nên ta có phương trình:

$\frac{60}{\mathrm{x}+1}+\frac{25}{\mathrm{x}-1}+\frac{1}{2}=8$(do xuồng nghỉ ở B 30 phút)

$$\begin{gathered} \iff \frac{2.60\left(\mathrm{x}-1\right)}{2.\left(\mathrm{x}-1\right)\left(\mathrm{x}+1\right)}+\frac{25.2.\left(\mathrm{x}+1\right)}{2.\left(\mathrm{x}-1\right)\left(\mathrm{x}+1\right)}+\frac{\left(\mathrm{x}-1\right)\left(\mathrm{x}+1\right)}{2\left(\mathrm{x}-1\right)\left(\mathrm{x}+1\right)}=\frac{16.\left(\mathrm{x}-1\right)\left(\mathrm{x}+1\right)}{2\left(\mathrm{x}-1\right)\left(\mathrm{x}+1\right)} \\ \Rightarrow 120\mathrm{x}-120+50\mathrm{x}+50+{\mathrm{x}}^2-1=16{\mathrm{x}}^2-16 \\ \iff 16{\mathrm{x}}^2-16-120\mathrm{x}+!20-50\mathrm{x}-50-{\mathrm{x}}^2+1=0 \\ \iff 15{\mathrm{x}}^2-170\mathrm{x}+55=0\left(*\right) \\ ∆={170}^2-15.4.55=25600 \\ \Rightarrow \sqrt{∆}=\sqrt{25600}=160 \end{gathered}$$

Phương trình (*) có hai nghiệm phân biệt

${\mathrm{x}}_1=\frac{170+160}{2.15}=11$(thỏa mãn);

${\mathrm{x}}_2=\frac{170-160}{2.15}=\frac{1}{3}$(loại vì x > 1)

Vậy vận tốc của xuồng khi nước đứng yên là 11km/h

Câu 2: Một công ty vận tải được điều một số xe chở 90 tấn hàng khi đến kho chở thì 2 xe bị hỏng nên để chở hết số hàng thì mỗi xe trở thêm 0,5 tấn so với dự định ban đầu. Hỏi số xe ban đâu được điều đến là bao nhiêu xe? Biết mỗi xe trở số hàng là như nhau.

Lời giải:

Gọi số xe ban đầu được điều đến chở hàng là x $\left(\mathrm{x}\in \mathrm{N}*; \mathrm{x}>2\right)$

Một xe ban đầu phải chở số tấn hàng là: $\frac{90}{\mathrm{x}}$(tấn)

Nhưng trên thực tế, số xe đã trở hàng là x – 2 (do 2 xe hỏng)

Do đó, một xe phải chở số tấn hàng là $\frac{90}{\mathrm{x}-2}$(tấn).

Vì mỗi xe phải trở thêm 0,5 tấn hàng nên ta có phương trình:

$\frac{90}{\mathrm{x}-2}-\frac{90}{\mathrm{x}}=0,5$

$$\begin{gathered} \iff \frac{90\mathrm{x}}{\mathrm{x}\left(\mathrm{x}-2\right)}-\frac{90\left(\mathrm{x}-2\right)}{\mathrm{x}\left(\mathrm{x}-2\right)}=\frac{1}{2} \\ \iff \frac{90\mathrm{x}-90\mathrm{x}+180}{\mathrm{x}\left(\mathrm{x}-2\right)}=\frac{1}{2} \\ \iff \frac{180}{\mathrm{x}\left(\mathrm{x}-2\right)}=\frac{1}{2} \\ \iff \mathrm{x}\left(\mathrm{x}-2\right)=360 \\ \iff {\mathrm{x}}^2-2\mathrm{x}-360=0\left(*\right) \\ ∆\text{'}=\mathrm{b}{\text{'}}^2-\mathrm{ac}={\left(-1\right)}^2-1.\left(-360\right)=361 \\ \Rightarrow \sqrt{∆\text{'}}=\sqrt{361}=19 \end{gathered}$$

Phương trình (*) có hai nghiệm phân biệt

${\mathrm{x}}_1=\frac{1+19}{1}=20$ (thảo mãn)

${\mathrm{x}}_2=\frac{1-19}{1}=-18$ (loại)

Vậy số xe ban đầu là 20 xe.

Câu 3: Một phân số có tử số bé hơn mẫu số là 11. Nếu bớt tử số đi 7 đơn vị và tăng mẫu số lên 4 đơn vị ta được phân số mới là nghịch đảo của phân số đã cho. Tìm phân số đó.

Lời giải:

Gọi tử số của phân số đó là x; mẫu số của phân số đó là x + 11 (do mẫu số lớn hơn tử số 11 đơn vị).

Phân số chúng ta cần tìm là: $\frac{\mathrm{x}}{\mathrm{x}+11}$(x là các số nguyên và x khác – 11)

Khi bớt tử số đi 7 đơn vị thì tử số mới là x – 7

Khi tăng mẫu số thêm 4 đơn vị thì mẫu số mới là x + 11 + 4 = x + 15

Phân số mới ta nhận được là $\frac{\mathrm{x}-7}{\mathrm{x}+15}$

Vì phân số mới là nghịch đảo của phân số ban đầu nên ta có:

$\frac{\mathrm{x}}{\mathrm{x}+11}=\frac{\mathrm{x}+15}{\mathrm{x}-7}$($\mathrm{x}\in \mathrm{Z}; \mathrm{x}\ne -11; \mathrm{x}\ne -15; \mathrm{x}\ne 7$)

$$\begin{gathered} \iff \frac{\mathrm{x}\left(\mathrm{x}-7\right)}{\left(\mathrm{x}+11\right)\left(\mathrm{x}-7\right)}=\frac{\left(\mathrm{x}+15\right)\left(\mathrm{x}+11\right)}{\left(\mathrm{x}+11\right)\left(\mathrm{x}-7\right)} \\ \iff \mathrm{x}\left(\mathrm{x}-7\right)=\left(\mathrm{x}+15\right)\left(\mathrm{x}+11\right) \\ \iff {\mathrm{x}}^2-7\mathrm{x}={\mathrm{x}}^2+15\mathrm{x}+11\mathrm{x}+165 \\ \iff -7\mathrm{x}-15\mathrm{x}-11\mathrm{x}=165 \\ \iff -33\mathrm{x}=165 \\ \iff \mathrm{x}=-5 \\ \Rightarrow \frac{\mathrm{x}}{\mathrm{x}+11}=\frac{-5}{6} \end{gathered}$$

Vậy phân số ban đầu là $\frac{-5}{6}$.

Gọi x là chữ số hàng chục. Điều kiện: x ∈ N*, x ≤ 9

Ta có chữ số hàng đơn vị là 10 – x

Giá trị của số cần tìm là: 10x + 10 – x = 9x + 10

Vì tích của hai chữ số nhỏ hơn chữ số đã cho là 12 nên ta có phương trình:

x(10 – x) = 9x + 10 – 12

⇔ 10x – x² = 9x – 2

⇔ x² – x – 2 = 0

Phương trình x² – x – 2 = 0 có hệ số a = 1, b = –1, c = –2 nên có dạng :

a – b + c = 0 suy ra: x₁ = –1 (loại), x₂ = $\frac{-c}{a}=\frac{2}{1}=2$  (thỏa mãn)

Vậy chữ số hàng chục là 2, chữ số hàng đơn vị là 10 – 2 = 8

Vậy số cần tìm là 28.

Gọi x (dãy) là số dãy ghế ban đầu của phòng họp.

Điều kiện: x ∈ N*

Khi đó số ghế ngồi trong một dãy là: $\frac{360}{x}$(ghế)

Số dãy ghế sau khi tăng là x + 1 (dãy)

Số ghế ngồi trong một dãy sau khi tăng là: $\frac{400}{x+1}$(ghế)

Theo đề bài, ta có phương trình: $\frac{400}{x+1}-\frac{360}{x}=1$

$\iff \frac{400x}{x\left(x+1\right)}-\frac{360\left(x+1\right)}{x\left(x+1\right)}=\frac{x\left(x+1\right)}{x\left(x+1\right)}$

$\iff 400x-360\left(x+1\right)=x\left(x+1\right)$

⇔ 400x – 360x – 360 = x² + x

⇔ x² – 39x + 360 = 0

∆ = (–39)² – 4.1.360 = 1521 – 1440 = 81 > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{39+\sqrt{81}}{2.1}=\frac{48}{2}=24;$

$x_2=\frac{39-\sqrt{81}}{2.1}=\frac{30}{2}=15$

Vậy bình thường phòng có 15 hoặc 24 dãy ghế.

Gọi x (km/h) là vận tốc của máy bay cánh quạt. Điều kiện: x > 0

Ta có vận tốc của máy bay phản lực là x + 300 (km/h)

Thời gian máy bay cánh quạt bay là $\frac{600}{x}$(giờ)

Thời gian máy bay phản lực bay là $\frac{600}{x+30}$(giờ)

Máy bay phản lực bay sau 10 phút và đến trước 10 phút nên thời gian máy bay phản lực bay ít hơn máy bay cánh quạt là:

10 phút + 10 phút = 20 phút = $\frac{1}{3}$(giờ)

Theo đề bài, ta có phương trình:

$\frac{600}{x}-\frac{600}{x+300}=\frac{1}{3}$

$\iff \frac{600.3\left(x+300\right)}{3.x\left(x+300\right)}-\frac{600.3x}{3.x\left(x+300\right)}=\frac{x\left(x+300\right)}{3.x\left(x+300\right)}$

$\iff 3.600\left(x+300\right)-3.600x=x\left(x+300\right)$

$\iff 1800x+540000-1800x=x^2+300x$

$\iff x^2+300x-540000=0$

$\Delta \text{'}={150}^2-1.\left(-540000\right)=22500+540000=562500>0$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-150+\sqrt{562500}}{1}=600$(thỏa mãn)

$x_2=\frac{-150-\sqrt{562500}}{1}=-900$(loại)

Vậy vận tốc của máy bay cánh quạt là 600km/h

Vận tốc của máy bay phản lực là 600 + 300 = 900 km/h.

Gọi x (km/h) là vận tốc lúc về. Điều kiện: x > 0

Ta có vận tốc lúc đi là x + 10 (km/h)

Thời gian lúc đi là $\frac{150}{x+10}$(giờ)

Thời gian lúc về là $\frac{150}{x}$(giờ)

Thời gian nghỉ là 3 giờ 15 phút = $\frac{13}{4}$(giờ)

Vì tổng thời gian đi, thời gian về, và thời gian nghỉ lại là 10 giờ nên ta có phương trình:

$\frac{150}{x+10}+\frac{150}{x}+\frac{13}{4}=10$

$\iff \frac{150}{x+10}+\frac{150}{x}=10-\frac{13}{4}$

$\iff \frac{150}{x+10}+\frac{150}{x}=\frac{27}{4}$

$\iff \frac{150.4x}{4x\left(x+10\right)}+\frac{150.4\left(x+10\right)}{4.x\left(x+10\right)}=\frac{27x\left(x+10\right)}{4x\left(x+10\right)}$

$\iff 600x+600\left(x+10\right)=27x\left(x+10\right)$

$\iff 600x+600x+6000=27x^2+270x$

$\iff 27x^2-930x-6000=0$

$\iff 9x^2-310x-2000=0$

$\Delta \text{'}={\left(-155\right)}^2-9.\left(-2000\right)=24025+18000=42025>0$

Phương trình có hai nghiệm phân biệt

$x_1=\frac{155+\sqrt{42025}}{9}=40$(thỏa mãn);

$x_2=\frac{155-\sqrt{42025}}{9}=\frac{-50}{9}$(loại)

Vậy vận tốc lúc về của ô tô là 40km/h

 

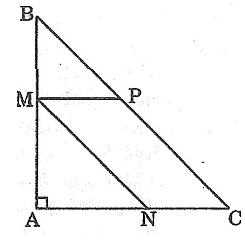
Gọi x (cm) là độ dài đoạn AM.

Điều kiện: 0 < x < 12

Vì ΔABC vuông cân tại A nên ΔBMP vuông cân tại M.

Suy ra MP = MB = AB – AM = 12 – x (cm)

Diện tích hình bình hành MNCP bằng MP.MA = (12 – x)x (cm²)

Theo đề bài, ta có phương trình:

(12 – x)x = 32

⇔ x² – 12x + 32 = 0

Δ' = (–6)² – 1.32 = 36 – 32 = 4 > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{6+\sqrt{4}}{1}=8$(thỏa mãn)

$x_2=\frac{6-\sqrt{4}}{1}=4$(thỏa mãn)

Vậy điểm M cách điểm A 8cm hoặc 4cm thì diện tích hình bình hành MNCP bằng 32cm².

Hai nông dân đem 100 quả trứng ra chợ bán. Số trứng của hai người không trùng nhau, nhưng hai người bán được một số tiền bằng nhau. Một người nói với người kia: “Nếu số trứng của tôi bằng số trứng của anh thì tôi bán được 15 đồng”. Người kia nói: “Nếu số trứng của tôi bằng số trứng của anh thì tôi chỉ bán được $6\frac{2}{3}$đồng thôi”. Hỏi mỗi người có bao nhiêu trứng?

Gọi x (quả) là số trứng của người thứ nhất.

Điều kiện: x ∈ N*, x < 100

Khi đó số trứng của người thứ hai là 100 – x (quả)

Nếu số trứng của người thứ nhất bằng số trứng của người thứ hai thì người thứ nhất bán được 15 đồng nên giá tiền một quả trứng của người thứ nhất là $\frac{15}{100-x}$(đồng)

Nếu số trứng của người thứ hai bằng số trứng của người thứ nhât thì người thứ hai bán được $6\frac{2}{3}$=$\frac{20}{3}$ đồng nên giá tiền một quả trứng của người thứ hai là $\frac{20}{3x}$(đồng).

Số tiền người thứ nhất bán được là:

$\frac{15}{100-x}.x=\frac{15x}{100-x}$(đồng)

Số tiền người thứ hai bán được là:

$\frac{20}{3x}\left(100-x\right)=\frac{20\left(100-x\right)}{3x}$(đồng)

Theo đề bài ta có phương trình:

$\frac{15x}{100-x}=\frac{20\left(100-x\right)}{3x}$

⇔ 45x² = 20(100 – x)²

⇔ 45x² = 20(10000 – 200x + x²)

⇔ 45x² = 200000 – 4000x + 20x²

⇔ 25x² + 4000x – 200000 = 0 ⇔ x² + 160x – 8000 = 0

∆' = 80² – 1.(–8000) = 6400 + 8000 = 14400 > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-80+\sqrt{14400}}{1}=40$(thỏa mãn)

$x_2=\frac{-80-\sqrt{14400}}{1}=-200$(loại)

Vậy số trứng của người thứ nhất là 40 quả

Số trứng của người thứ hai là 100 – 40 = 60 quả.

Một đàn khỉ chia thành hai nhóm

Nhóm chơi đùa vui vẻ ngoài trời

Bằng bình phương một phần tám của đàn

Mười hai con nhảy nhót trên cây

Không khí tươi vui sưởi ấm nơi này

Hỏi có tất cả bao nhiêu con khỉ?

Gọi x (con) là số khỉ trong đàn. Điều kiện: x ∈N*, x chia hết 8

Khi đó nhóm chơi đùa ngoài trời có ${\left(\frac{x}{8}\right)}^2$(con)

Nhóm nhảy nhót trên cây có 12 (con)

Theo bài ra ta có phương trình:
x = 12 + $\frac{x^2}{64}$

$\iff x^2-64x+12=0$

∆' = (–32)² – 1.768 = 1024 – 768 = 256 > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{32+\sqrt{256}}{1}=48$(thỏa mãn)

$x_2=\frac{32-\sqrt{256}}{1}=16$(thỏa mãn)

Vậy đàn khỉ có 48 con hoặc 16 con.

III. Bài tập vận dụng

Câu 1: Một đội xe cần chở 480 tấn hàng. Khi bắt đầu làm việc, có hai xe bị điều động đi làm việc khác, vì vậy mỗi xe phải chở thêm 1 tấn nữa mới hết số hàng cần chở. Hỏi lúc đầu, đội đó có bao nhiêu xe ?

Câu 2: Cạnh huyền của một tam giác vuông bằng 19,5cm. Tính độ dài các cạnh góc vuông, biết chu vi tam giác vuông là 45cm.

Câu 3: Hiệu giữa hai số là 3 và tích của chúng là 648. Tìm hai số đó.

Câu 4: Một chiếc thuyền chở du khách đi ngược dòng suối từ bến A đến bến B cách nhau 5 Sau khi đến bến B, du khách nghỉ 40 phút rồi lại lên thuyền đi xuôi dòng suối về bến A. Tổng thời gian của cả chuyến đi là 2 giờ. Biết vận tốc của dòng suối là 2 km/h. Tính vận tốc của thuyền khi nước yên lặng.

Câu 5: Một lớp học sinh tham gia lao động, dự kiến chuyển 150 bộ bàn ghế từ cổng trường vào các lớp. Đến buổi lao động thì 5 bạn được cô giáo chủ nhiệm chuyển đi làm việc khác. Vì vậy, mỗi bạn còn lại phải chuyển thêm 1 bộ bàn ghế nữa mới hết số bàn ghế cần chuyển. Tính số học sinh của lớp lúc ban đầu.

Câu 6: Một cái hộp không nắp được làm từ một mảnh bìa kích thước 20cm x 30cm bằng cách cắt ở bốn góc bốn hình vuông bằng nhau. Diện tích phần đáy hộp là 144cm . Tính độ dài mỗi cạnh hình vuông cắt ra ở mỗi góc.

Câu 7: Hai vòi nước cùng chảy vào một cái bể không có nước trong 4 giờ 48 phút sẽ đầy bể. Nếu chảy riêng thì vòi 1 chảy đầy bể nhanh hơn vòi là 4 giờ. Hỏi mỗi vòi chảy một mình thì trong bao lâu mới đầy bể ?

Câu 8: Một mảnh đất hình chữ nhật có chiều rộng 80m và chiều dài 120m. Trên mảnh đất đó người ta đào một cái hồ hình chữ nhật, xung quanh có một dải cỏ bao quanh hồ. Biết diện tích của hồ bằng  diện tích của mảnh đất ban đầu. Tính bề rộng của dải cỏ.

Câu 9: Hai chiếc tàu hoả A và B rời đi từ cùng một thành phố p vào cùng một thời điểm, theo hướng tây và hướng nam tương ứng. Vận tốc tàu A lớn hơn tàu B 14 km/h. Sau 5 giờ hai tàu cách nhau 130 Tìm vận tốc của mỗi tàu.

Câu 10: Hai địa điểm A và B cách nhau 215 km. Lúc 7 giờ sáng, một người đi xe máy đi từ A đến B . Sau đó, vào lúc 8 giờ, người thứ hai đi xe máy xuất phát từ B để đi đến A. Hai người gặp nhau tại địa điểm c cách B 80 kilômét. Biết rằng vận tọc xe thứ nhất lớn hơn vận tốc xe thứ hai là 5km/h và cả hai xe đều đi với vận tốc lớn hơn 30km/h. Hỏi hai người gặp nhau lúc mấy giờ ?

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Bài tập ôn tập chương

Chuyên đề Góc ở tâm. Số đo cung

Chuyên đề Liên hệ giữa cung và dây

Chuyên đề Góc nội tiếp

Chuyên đề Góc tạo bởi tia tiếp tuyến và dây cung