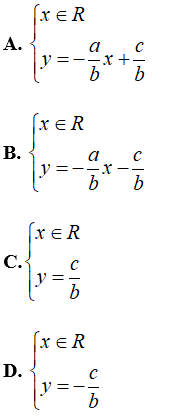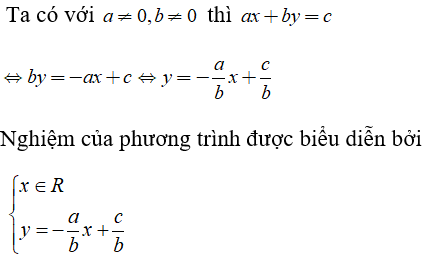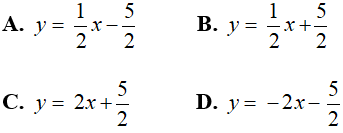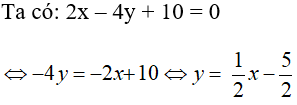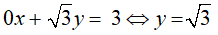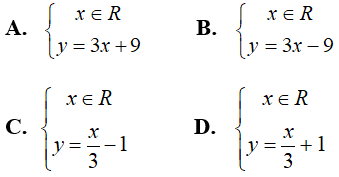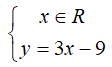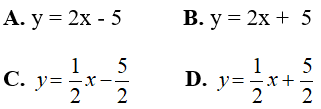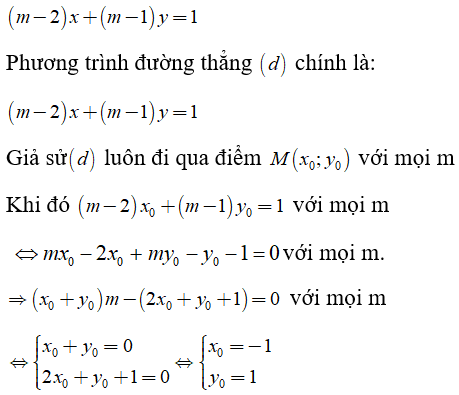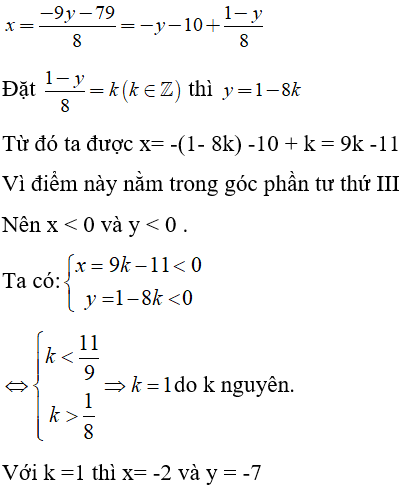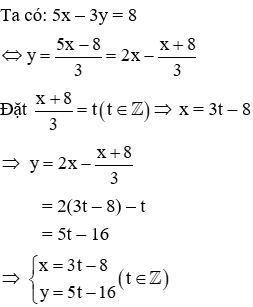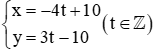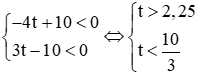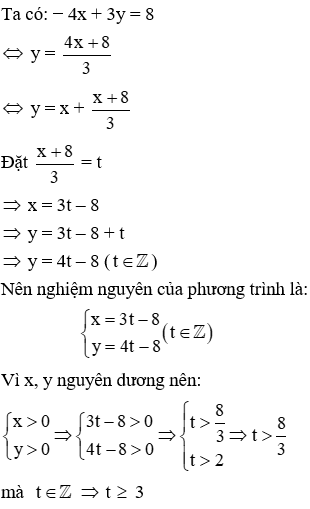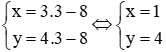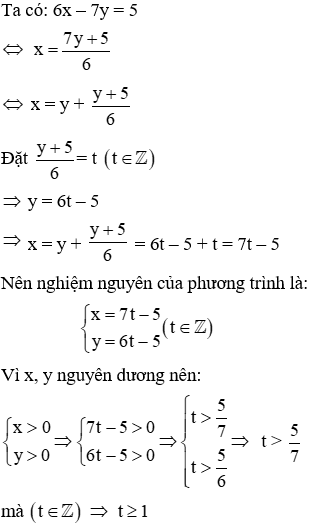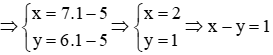Chuyên đề Phương trình bậc nhất hai ẩn (2022) - Toán 9

Chuyên đề Phương trình bậc nhất hai ẩn - Toán 9

A. Lý thuyết

1. Khái niệm về phương trình bậc nhất hai ẩn

- Khái niệm phương trình bậc nhất hai ẩn: Phương trình bậc nhất hai ẩn x và y là hệ thức dạng

ax + by = c (1)

trong đó a, b, c là các số đã biết (a hoặc b )

Ví dụ 1:

2x + 3y = 5

4x + 6y = 7

-2x – 3y = 4

Các phương trình trên là những ví dụ về phương trình bậc nhất hai ẩn. Hai ẩn ở đây là x và y.

- Trong phương trình (1), nếu giá trị của vế trái tại x = x₀ và y = y₀ bằng vế phải thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình.

Ta cũng viết: Phương trình (1) có nghiệm là (x; y) = (x₀; y₀).

Chú ý:

- Trong mặt phẳng tọa độ Oxy mỗi nghiệm của phương trình ax + by = c được biểu diễn bởi một điểm. Nghiệm (x₀; y₀) được biểu diễn bởi điểm có tọa độ (x₀; y₀).

- Khái niệm tập nghiệm và khái niệm phương trình tương đương của phương trình bậc nhất hai ẩn cũng tương tự như đối với phương trình bậc nhất một ẩn. Ngoài ra ta cũng có thể áp dụng quy tắc chuyển vế hoặc quy tắc nhân đã học để biến đổi phương trình bậc nhất hai ẩn.

2. Tập nghiệm của phương trình bậc nhất hai ẩn

- Phương trình bậc nhất hai ẩn: ax + by = c luôn luôn có vô số nghiệm. Tập nghiệm của nó được biêu diễn bởi đường thẳng ax + by = c, kí hiệu là (d).

- Nếu  và  thì đường thẳng (d) chính là đồ thị của hàm số bậc nhất

y = $-\frac{\mathrm{a}}{\mathrm{b}}x+\frac{\mathrm{c}}{\mathrm{b}}$

- Nếu a và b = 0 thì phương trình trở thành ax = c hay x = $\frac{\mathrm{c}}{\mathrm{a}}$, và đường thẳng (d) song song với trục tung hoặc trùng với trục tung.

- Nếu a = 0 và b  thì phương trình trở thành by = c hay $\mathrm{y}=\frac{\mathrm{c}}{\mathrm{b}}$, và đường thẳng (d) song song hoặc trùng với trục hoành.

Nói cách khác, ta có công thức nghiệm tổng quát như sau:

- Nếu $\mathrm{a}\ne 0$ và $\mathrm{b}\ne 0$ thì công thức nghiệm là:

$\left\{\begin{array}{l}\mathrm{x}\in \mathrm{R}\\ \mathrm{y}=\frac{\mathrm{c}-\mathrm{ax}}{\mathrm{b}}\end{array}\right.$hoặc $\left\{\begin{array}{l}\mathrm{x}=\frac{\mathrm{c}-\mathrm{by}}{\mathrm{a}}\\ \mathrm{y}\in \mathrm{R}\end{array}\right.$

Khi đó (d) cắt cả hai trục Ox; Oy

Ví dụ 2: x – y = 1 có $\mathrm{a}\ne 0$ và $\mathrm{b}\ne 0$, khi đó công thức nghiệm là:

$\left\{\begin{array}{l}\mathrm{x}\in \mathrm{R}\\ \mathrm{y}=\mathrm{x}-1\end{array}\right.$ hoặc $\left\{\begin{array}{l}\mathrm{x}=\mathrm{y}+1\\ \mathrm{y}\in \mathrm{R}\end{array}\right.$

- Nếu a = 0 và $\mathrm{b}\ne 0$ thì công thức nghiệm là:

$\left\{\begin{array}{l}\mathrm{x}\in \mathrm{R}\\ \mathrm{y}=\frac{\mathrm{c}}{\mathrm{b}}\end{array}\right.$và (d) // Ox

Ví dụ 3: Phương trình 0x + y = 5 có a = 0 và $\mathrm{b}\ne 0$, khi đó công thức nghiệm là:

$\left\{\begin{array}{l}\mathrm{x}\in \mathrm{R}\\ \mathrm{y}=5\end{array}\right.$

- Nếu $\mathrm{a}\ne 0$ và b = 0 thì công thức nghiệm là:

$\left\{\begin{array}{l}\mathrm{x}=\frac{\mathrm{c}}{\mathrm{a}}\\ \mathrm{y}\in \mathrm{R}\end{array}\right.$và (d) // Oy

Ví dụ 4: Phương trình 2x + 0y = 3 có $\mathrm{a}\ne 0$ và b = 0, khi đó công thức nghiệm là:

$\left\{\begin{array}{l}\mathrm{x}=\frac{\mathrm{c}}{\mathrm{a}}\\ \mathrm{y}\in \mathrm{R}\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=\frac{3}{2}\\ \mathrm{y}\in \mathrm{R}\end{array}\right.\right.$

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Cho phương trình ax + by = c với a ≠0, b ≠ 0 . Nghiệm của phương trình được biểu diễn bởi

Lời giải:

Chọn đáp án A

Câu 2: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

Lời giải:

Phương trình  là phương trình bậc nhất hai ẩn.

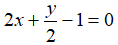
Chọn đáp án C

Câu 3: Phương trình nào dưới đây nhận cặp số (-2; 4) làm nghiệm

A. x - 2y = 0

B. 2x + y = 0

C. x - y = 0

D. x + 2y + 1 = 0

Lời giải:

Chọn đáp án B

Câu 4: Phương trình x - 5y + 7 = 0 nhận cặp số nào sau đây là nghiệm?

A. (0; 1)

B. (-1; 2)

C. (3; 2)

D. (2; 4)

Lời giải:

+ Thay x = 0; y = 1 vào phương trình x - 5y + 7 = 0 ta được 0 - 5.1 + 7 = 0 ⇔ 2 = 0 (vô lí) nên loại A

+ Thay x = -1; y = 2 vào phương trình x - 5y + 7 = 0 ta được -1 – 5.2 + 7 = 0 hay – 4 = 0 ⇒ (vô lí) nên loại B

+ Thay x = 2; y = 4 vào phương trình x - 5y + 7 = 0 ta được 2 - 5.4 + 7 = 0 ⇔ -11 = 0 (vô lí) nên loại D

+ Thay x = 3; y = 2 vào phương trình x - 5y + 7 = 0 ta được 3 - 5.2 + 7 = 0 ⇔ 0 = 0 (luôn đúng) nên chọn C

Chọn đáp án C

Câu 5: Tìm m để phương trình 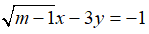 nhận cặp số (1; 1) làm nghiệm

A. m = 5

B. m = 2

C. m = -5

D. m = -2

Lời giải:

Chọn đáp án A

Câu 6: Cho phương trình 2x – 4y + 10 = 0 . Tập nghiệm của phương trình trên được biểu diễn bởi đường thẳng ?

Lời giải:

Chọn đáp án A.

Câu 7: Cho phương trình 2x – 6 = 0. Đường thẳng biểu diễn tập nghiệm của phương trình trên là đường thẳng?

A. Song song trục hoành

B. Song song trục tung.

C. Song song đường thẳng x - 3 = 0

D. Trùng với đường thẳng 3x + 9 = 0

Lời giải:

Ta có: 2x - 6 = 0 ⇔ 2x = 6 ⇔ x = 3 Do đó, đường thẳng biểu diễn tập nghiệm phương trình đã cho là đường thẳng song song trục tung Oy.

Chọn đáp án B.

Câu 8: Cho phương trình: 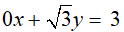 . Đường thẳng biểu diễn tập nghiệm của phương trình trên là đường thẳng :

A. Song song đường thẳng

B. Song song trục tung.

C. Song song trục hoành.

D. Song song với đường thẳng

Lời giải:

Ta có:

Do đó, đường thẳng biểu diễn tập nghiệm của phương trình đã cho là đường thẳng song song trục hoành.

Chọn đáp án C.

Câu 9: Cho phương trình : 3x - y = 9. Nghiệm tổng quát của phương trình là:

Lời giải:

Ta có: Do đó, nghiệm tổng quát của phương trình đã cho là 

Chọn đáp án B.

Câu 10: Cho phương trình: 5x – 10y = 25. Tìm nghiệm tổng quát của phương trình đã cho?

Lời giải:

Chọn đáp án C.

II. Bài tập tự luận có lời giải

Câu 1: Tìm hai nghiệm của phương trình x + y = 2 (1)

Lời giải:

    + Cho y = 0 ⇒ x = 2 → (2; 0) là một nghiệm của phương trình (1).

    + Cho y = 1 ⇒ x = 1 → (1; 1) là một nghiệm của phương trình (1).

⇒ (2; 0); (1; 1) là hai nghiệm cần tìm của phương trình x + y = 2.

Câu 2: Cho hai cặp số (1; 2) và (0; 1). Hỏi cặp nào là nghiệm của phương trình 2x + 3y = 8 ?

Lời giải:

    + Ta có 2.1 + 3.2 = 8 ⇒ (1; 2) là cặp nghiệm của phương trình 2x + 3y = 8.

    + Ta có 2.0 + 3.1 = 3 ≠ 8 ⇒ (0; 1) không phải là cặp nghiệm của phương trình 2x + 3y = 8

Câu 3: Cặp số (1:1) có phải là nghiệm của phương trình x + y = 1 không?

Lời giải:

Ta có: 1 + 1 = 2 ≠ 1 nên (1;1) không là nghiệm của phương trình x+ y = 1

Câu 4: Cho phương trình (m - 2)x + (m - 1)y = 1 (m là tham số). Chứng minh rằng đường thẳng biểu diễn tập nghiệm của phương trình này luôn đi qua một điểm cố định với mọi giá trị của m

Lời giải:

Gọi (d) là đường thẳng biểu diễn tập nghiệm của phương trình

Vậy (d) luôn đi qua một điểm cố định là M(-1; 1)

Câu 5: Tìm các điểm nằm trên đường thẳng 8x + 9y = -79 , có hoành độ và tung độ là các số nguyên và nằm trong góc vuông phần tư thứ III

Lời giải:

Ta cần tìm nghiệm nguyên của phương trình 8x + 9y = -79 , rút x từ phương trình ta được:

Vậy có 1 điểm duy nhất phải tìm là (-2; -7)

Câu 6: Tìm tất cả nghiệm nguyên của phương trình 5x – 3y = 8

Lời giải:

Câu 7: Tìm nghiệm nguyên âm lớn nhất của phương trình −5x + 2y = 7

Lời giải:

Câu 8: Tìm nghiệm nguyên âm của phương trình 3x + 4y = −10 là (x; y). Tính x.y

Lời giải:

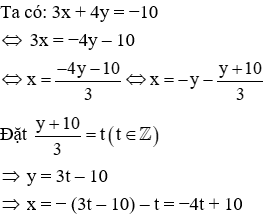
Hay nghiệm nguyên của phương trình 3x + 4y = −10 là 

Vì x; y nguyên âm hay x < 0; y < 0 nên 

mà t ∈ Z ⇒ t = 3

Suy ra x = −4.3 + 10 = −2; y = 3.3 – 10 = −1 nên nghiệm nguyên âm cần tìm là (a; y) = (−2; −1) ⇒ x.y = 2

Câu 9: Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình −4x + 3y = 8. Tính x + y

Lời giải:

Nghiệm nguyên dương nhỏ nhất của phương trình là 

⇒ x + y = 5

Câu 10: Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình 6x − 7y = 5. Tính x – y

Lời giải:

Do đó nghiệm nguyên dương nhỏ nhất của phương trình có được khi t = 1

III. Bài tập vận dụng

Câu 1: Tìm hai nghiệm của phương trình x + y = 2 (1)

Câu 2: Cho hai cặp số (1; 2) và (0; 1). Hỏi cặp nào là nghiệm của phương trình 2x + 3y = 8 ?

Câu 3: Cặp số (1:1) có phải là nghiệm của phương trình x + y = 1 không?

Câu 4: Cho phương trình (m - 2)x + (m - 1)y = 1 (m là tham số). Chứng minh rằng đường thẳng biểu diễn tập nghiệm của phương trình này luôn đi qua một điểm cố định với mọi giá trị của m

Câu 5: Tìm các điểm nằm trên đường thẳng 8x + 9y = -79 , có hoành độ và tung độ là các số nguyên và nằm trong góc vuông phần tư thứ III

Câu 6: Tìm hai nghiệm của phương trình: 3x – 2y = 4

Câu 7: Trong các cặp số (0; 2); (3; 5); (1; 4) cặp số nào là nghiệm của phương trình 2x + y = 6.

Câu 8: Tìm m để cặp số (2; 3) là nghiệm của phương trình x – 3y = m + 2

Câu 9: Cho đường thẳng d có phương trình (m – 2)x + (3m – 1)y = 6m – 2. Tìm các giá trị của tham số m để d đi qua gốc tọa độ.

Câu 10: Tìm nghiệm nguyên âm lớn nhất của phương trình −5x + 2y = 7

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Hệ phương trình bậc nhất hai ẩn

Chuyên đề Giải hệ phương trình bằng phương pháp thế

Chuyên đề Giải hệ phương trình bằng phương pháp cộng đại số

Chuyên đề Giải bài toán bằng cách lập hệ phương trình

Chuyên đề Ôn tập chương 3