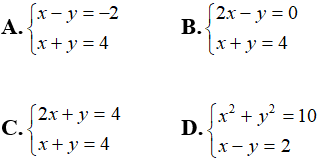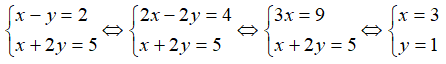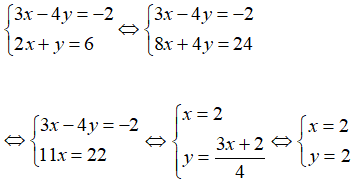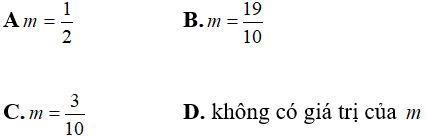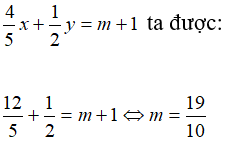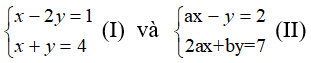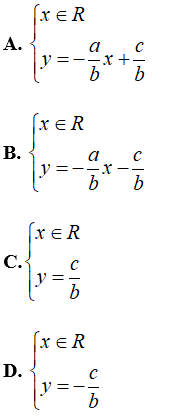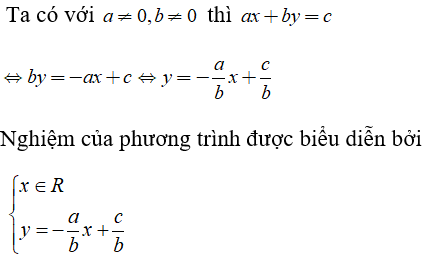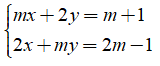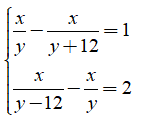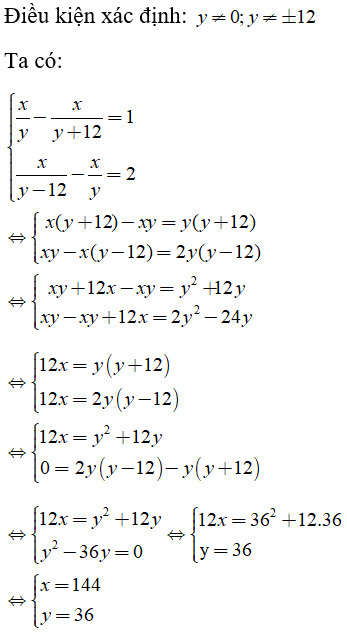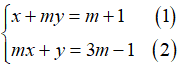Chuyên đề Ôn tập chương 3 (2022) - Toán 9
Với Chuyên đề Ôn tập chương 3 (2022) - Toán 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Ôn tập chương 3 - Toán 9
A. Lý thuyết
1. Phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng
ax + by = c (1)
trong đó a, b, c là các số đã biết (a hoặc b )
2. Nghiệm của phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn luôn có vô số nghiệm. Trong mặt phẳng tọa độ, tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c (d).
Nếu {a≠0b≠0 thì (d) là đồ thị của hàm số bậc nhất y=-abx+cb
3. Hệ phương trình bậc nhất hai ẩn và tập nghiệm của hệ phương trình bậc nhất hai ẩn
a) Hệ phương trình bậc nhất hai ẩn
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a’x + b’y = c’. Khi đó ta có hệ phương trình:
(I) {ax+by=ca'x+b'y=c'
b) Tập nghiệm của hệ phương trình bậc nhất hai ẩn
Gọi (d) và (d') là đồ thị hàm số của 2 hàm số rút ra từ 2 phương trình bậc nhất hai ẩn của (I).
Đối với hệ phương trình (I), ta có:
Nếu (d) cắt (d') thì hệ (I) có một nghiệm duy nhất.
Nếu (d) song song với (d') thì hệ (I) vô nghiệm.
Nếu (d) trùng với (d') thì hệ (I) có vô số nghiệm.
Nếu a; a'; b; b'; c; c' đều khác 0 thì:
Hệ phương trình có nghiệm duy nhất ⇔aa'≠bb';
Hệ phương trình vô nghiệm ⇔aa'=bb'≠cc';
Hệ phương trình vô số nghiệm ⇔aa'=bb'=cc'.
4. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế
Bước 1: Dùng quy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới, trong đó có một phương trình một ẩn.
Bước 2: Giải phương trình một ẩn đó rồi suy ra nghiệm của hệ đã cho.
5. Giải hệ phương trình bằng phương pháp cộng đại số
Bước 1: Nhân hai vế của mỗi phương trình với các số thích hợp (nếu cần) sao cho với một ẩn nào đó các hệ số bằng nhau hoặc đối nhau.
Bước 2: Áp dụng quy tắc cộng (trừ) đại số để được một hệ phương trình mới, trong đó một phương trình có hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
Bước 3: Giải phương trình một ẩn vừa có rồi suy ra nghiệm hệ phương trình.
6. Giải bài toán bằng cách lập phương trình
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Trả lời
Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
B. Bài tập
I. Bài tập trắc nghiệm
Câu 1: Cặp số (x; y) = (1; 3) là nghiệm của hệ phương trình bậc nhất hai ẩn nào trong các hệ phương trình sau:
Phương án D không phải là hệ phương trình bậc nhất hai ẩn nên loại D
Chọn đáp án A
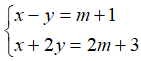 có cặp nghiệm (x; y) là:
có cặp nghiệm (x; y) là:A. (3; 1)
B. (1; 3)
C. (-1; -3)
D. (-3; -1)
Thay m = 1 vào hệ phương trình đã cho ta được:
Chọn đáp án A
Câu 3: Cặp số (x; y) là nghiệm của hệ phương trình: 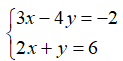
A. (-1; -2)
B. (2; 2)
C. (2; -1)
D. (3; 2)
Chọn đáp án B
Câu 4: Với giá trị nào của m thì hệ phương trình : 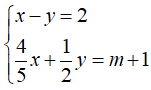
Nhận thấy 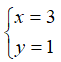
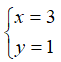
Chọn đáp án B
Câu 5: Tìm giá trị (a; b) để hai phương trình sau tương đương:
A. (-1; -1)
B. (1; 2)
C. (-1; 1)
D. (1; 1)
Chọn đáp án D
Câu 6: Cho phương trình ax + by = c với a ≠0, b ≠ 0 . Nghiệm của phương trình được biểu diễn bởi
Chọn đáp án A
Câu 7: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
Phương trình 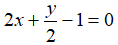
Chọn đáp án C
Câu 8: Phương trình nào dưới đây nhận cặp số (-2; 4) làm nghiệm
A. x - 2y = 0
B. 2x + y = 0
C. x - y = 0
D. x + 2y + 1 = 0
Chọn đáp án B
Câu 9: Phương trình x - 5y + 7 = 0 nhận cặp số nào sau đây là nghiệm?
A. (0; 1)
B. (-1; 2)
C. (3; 2)
D. (2; 4)
+ Thay x = 0; y = 1 vào phương trình x - 5y + 7 = 0 ta được 0 - 5.1 + 7 = 0 ⇔ 2 = 0 (vô lí) nên loại A
+ Thay x = -1; y = 2 vào phương trình x - 5y + 7 = 0 ta được -1 – 5.2 + 7 = 0 hay – 4 = 0 ⇒ (vô lí) nên loại B
+ Thay x = 2; y = 4 vào phương trình x - 5y + 7 = 0 ta được 2 - 5.4 + 7 = 0 ⇔ -11 = 0 (vô lí) nên loại D
+ Thay x = 3; y = 2 vào phương trình x - 5y + 7 = 0 ta được 3 - 5.2 + 7 = 0 ⇔ 0 = 0 (luôn đúng) nên chọn C
Chọn đáp án C
Câu 10: Tìm m để phương trình 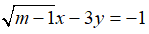
A. m = 5
B. m = 2
C. m = -5
D. m = -2
Chọn đáp án A
II. Bài tập tự luận có lời giải
Câu 1: Hệ phương trình 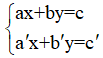
Câu 2: Hệ hai phương trình bậc nhất hai ẩn 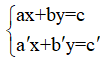
Câu 3: Tìm m nguyên để hệ có nghiệm duy nhất là nghiệm nguyên
Lời giải:
Câu 4: Giải hệ phương trình sau bằng phương pháp cộng đại số
Lời giải:
Vậy hệ phương trình có cặp nghiệm là (x; y) = (144; 36)
Câu 5: Viết phương trình bậc nhất hai ẩn có hai nghiệm là (2; 0) và (-1; -2).
Lời giải:
Vì nghiệm của phương trình bậc nhất hai ẩn nằm trên một đường thẳng nên ta gọi đường thẳng đó là d: y = ax + b.
+ Thay x = 2; y = 0 vào đường thẳng d ta có: 0 = 2.a + b (1)
+ Thay x = -1; y = -2 vào đường thẳng d ta có: -2 = -1.a + b (2)
Từ (2) ta có: b = -2 + a thay vào (1) ta có:
2.a + a – 2 =0
⇔3a – 2 = 0
⇔3a = 2
⇔a=23⇒b=-2+23=-43
Đường thẳng d cần tìm là y = 23x-43
⇒Phương trình bậc nhất hai ẩn là 2x – 3y – 4 = 0.
Câu 6: Giải hệ phương trình sau bằng phương pháp thế:
a) {x-y=33x-4y=2
b) {4,8x+4,8y=14x+3y=34
Lời giải:
a) {x-y=33x-4y=2
⇔{x=3+y3x-4y=2⇔{x=3+y3(3+y)-4y=2⇔{x=3+y9+3y-4y=2⇔{x=y+39-y=2⇔{x=y+3y=9-2⇔{x=y+3y=7⇔{x=7+3y=7⇔{x=10y=7
Vậy hệ phương trình đã cho có nghiệm (x; y) = (10; 7)
b) {4,8x+4,8y=14x+3y=34(x,
Đặt khi đó hệ trở thành
Câu 7: Giải hệ phương trình bằng phương pháp cộng đại số
a)
b)
Lời giải:
a)
(nhân cả hai vế phương trình thứ hai với 2)
(Trừ vế với vế của phương trình thứ nhất cho phương trình thứ hai)
Vậy hệ phương trình đã cho có nghiệm (x; y) = (3; -2).
b)
Đặt
Khi đó hệ phương trình trở thành
Nhân cả hai vế của phương trình (1) với 3 ta được hệ mới:
Lấy (3) + (4) ta được:
+ Với a = 10
+ Với b = 12
Vậy ta tìm được 4 cặp nghiệm (x; y) là (12; 13); (-8; 13); (12; -11); (-8; -11).
Câu 8: Hai tổ sản xuất cùng may một loại áo. Nếu tổ thứ 1 may trong 3 ngày, tổ thứ 2 may trong 5 ngày thì hai tổ may được 1310 chiếc áo. Biết rằng, trong một ngày tổ thứ 1 may được nhiều hơn tổ thứ 2 là 10 chiếc áo. Hỏi mỗi tổ trong một ngày may được bao nhiêu chiếc áo?
Lời giải:
Gọi lần lượt số áo tổ thứ 1, thứ 2 may trong một ngày là x, y.
Đk: x, y N*
Trong 3 ngày tổ thứ 1 may được là 3x (cái áo), trong 5 ngày tổ thứ 2 may được là 5y (cái áo) và cả hai tổ may được 1310 cái áo nên ta có phương trình: 3x + 5y = 1310 (1)
Mặt khác mỗi ngày tổ 1 may được nhều hơn tổ 2 10 chiếc áo nên ta có phương trình: x – y = 10 (2)
Theo bài ra ta có HPT:
Vậy tổ thứ 1 may được 170 chiếc áo trong một ngày, tổ thứ hai may được 160 chiếc áo trong một ngày
Câu 9: Hai đội công nhân cùng làm chung một công việc trong 4h thì xong. Nếu mỗi đội làm một mình xong công việc thì đội thứ nhất làm ít thời gian hơn so với đội thứ hai là 6h. Hỏi nếu mỗi đội làm một mình xong công việc ấy thì trong bao lâu?
Lời giải:
Gọi thời gian đội 1 làm một mình xong công việc là x (h)
Gọi thời gian đội 2 làm một mình xong công việc là y (h)
Điều kiện: (x > 0 ; y > 6 ; y > x)
Trong 1h đội 1 làm được (công việc)
Trong 1h đội 2 làm được (công việc)
Vì cả hai đội làm trong 4h thì xong công việc nên 1 h cả hai đội làm được công việc
Ta có phương trình: (1)
Vì mỗi đội làm một mình thì đội 1 làm ít hơn đội 2 6h nên ta có phương trình :
x – y = -6 (2)
Từ (1) và (2) ta có hệ phương trình:
Giải (1):
Với x = 6 thì y = 6 + 6 = 12
Vậy đội 1 làm một mình thì 6 giờ xong công việc
Đội 2 làm một mình thì 12 giờ xong công việc.
Câu 10: Một khu vườn hình chữ nhật có chu vi bằng 60m. Nếu tăng chiều dài lên 4 lần và chiều rộng lên 3 lần thì chu vi khu vườn sẽ tăng 162m. Tìm diện tích khu vườn.
Lời giải:
Gọi chiều dài của khu vườn là x (m); chiều rộng của khu vườn là y (m)
Vì chu vi khu vườn là 60m nên ta có phương trình:
2.(x + y) = 60
x + y = 60:2
x + y = 30 (1)
Nếu tăng chiều dài lên 4 lần thì chiều dài mới là 4x (m); nếu tăng chiều rộng lên 3 lần thì chiều rộng mới là 3y (m).
Chu vi khu vườn mới là: 2(4x + 3y) = 8x + 6y (m)
Vì chu vi khu vườn mới hơn chu vi khu vườn cũ 162m nên ta có phương trình:
(8x + 6y) – 2(x + y) = 162
8x + 6y – 2x – 2y = 162
6x + 4y = 162 (2)
Từ (1) và (2) ta có hệ phương trình:
Diện tích khu vườn ban đầu là:
S = 21.9 = 189
III. Bài tập vận dụng
Câu 1: Hai trường có tất cả 300 học sinh tham gia một cuộc thi. Biết trường A có 75% học sinh đạt, trường 2 có 60% đạt nên cả 2 trường có 207 học sinh đạt. Tính số học sinh dự thi của trường A và trường B
Câu 2: Cho hệ phương trình với tham số a 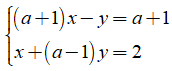
Câu 3: Hai người cùng làm chung 1 công việc dự định trong 12 giờ thì xong. Họ làm chung với nhau được 8 giờ thì người thứ nhất nghỉ, còn người thứ hai vẫn tiếp tục làm. Do cố gắng tăng năng suất gấp đôi nên người thứ hai đã làm xong phần việc còn lại trong 3 giờ 20 phút. Hỏi nếu mỗi người thợ ấy làm một mình với năng suất dự định ban đầu thì phải mất bao lâu làm xong công việc nói trên?
Câu 4: Cho hệ phương trình:
Tìm số nguyên m để hệ phương trình có nghiệm duy nhất (x; y) mà x, y đều là số nguyên.
Câu 5: Hai bạn A và B đi xe máy khởi hành từ 2 địa điểm cách nhau 150 km, đi ngược chiều nhau và gặp nhau sau 2h. Tìm vận tốc của mỗi người biết nếu A tăng vận tốc thêm 5 km/h và B giảm vận tốc 5 km/h thì vận tốc của A gấp đôi vận tốc của B.
Câu 6: Hai đội xe được điều đi chở đất. Nếu cả 2 đội cùng làm thì trong 12 ngày xong việc. Nhưng 2 đội chỉ cùng làm trong 8 ngày thì đội 2 phải đi làm việc khác nên đội 1 phải tiếp tục làm 1 mình trong 7 ngày thì xong việc. Hỏi mỗi đội làm 1 mình thì trong bao lâu xong việc.
Câu 7: Tháng thứ nhất, 2 tổ sản xuất được 1200 sản phẩm. Tháng thứ hai, tổ I vượt mức 30% và tổ II bị giảm năng suất 22% so với tháng thứ nhất. Vì vậy 2 tổ đã sản xuất được 1300 sản phẩm. Hỏi tháng thứ hai, tổ 2 sản xuất được bao nhiêu sản phẩm.
Câu 8: Giải các hệ phương trình sau:
a)
b)
c)
d)
Câu 9 Giải các hệ phương trình sau:
a)
b)
Câu 10: Hai xe lửa khởi hành đồng thời từ hai ga cách nhau 750km và đi ngược chiều nhau, sau 10 giờ chúng gặp nhau. Nếu xe thứ nhất khởi hành trước xe thứ hai 3 giờ 45 phút thì sau khi xe thứ hai đi được 8 giờ chúng gặp nhau. Tính vận tốc của mỗi xe.
Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:
Chuyên đề Hàm số y = ax^2 (a khác 0)
Chuyên đề Đồ thị của hàm số y = ax^2 (a khác 0)
Chuyên đề Phương trình bậc hai một ẩn
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9