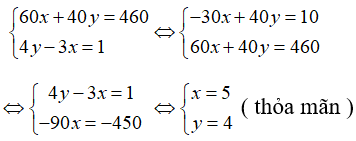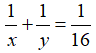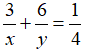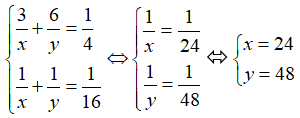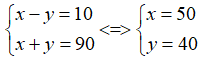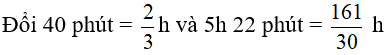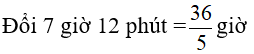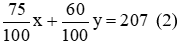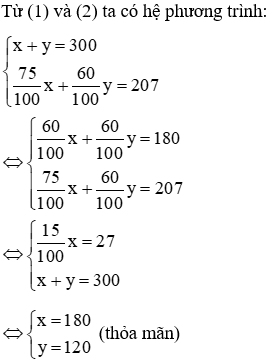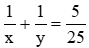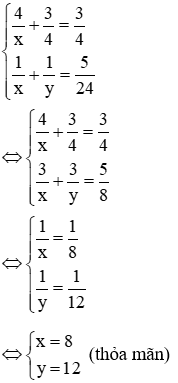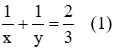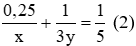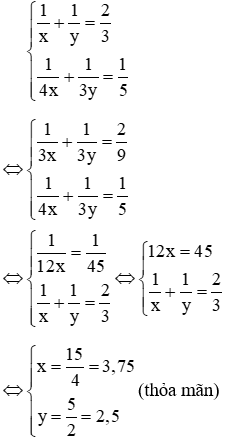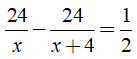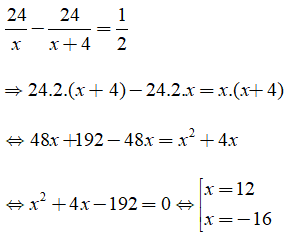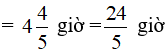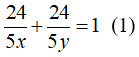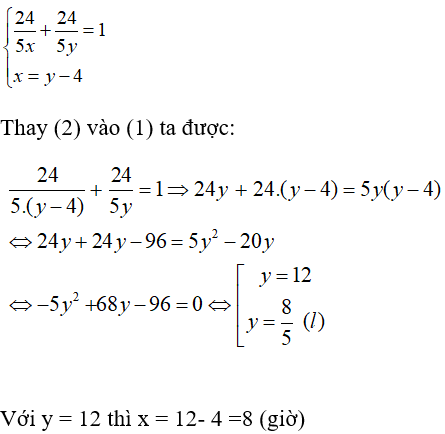Chuyên đề Giải bài toán bằng cách lập hệ phương trình (2022) - Toán 9

Chuyên đề Giải bài toán bằng cách lập hệ phương trình - Toán 9

A. Lý thuyết

1. Các bước giải bài toán bằng cách lập phương trình

Bước 1: Lập phương trình

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết

- Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình

Bước 3: Trả lời

Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

2. Lưu ý về chọn ẩn và điều kiện thích hợp của ẩn

- Thông thường thì bài toán hỏi về đại lượng gì thì chọn ẩn là đại lượng đó.

- Về điều kiện thích hợp của ẩn

+ Nếu x biểu thị một chữ số thì $0\le \mathrm{x}\le 9$, $\mathrm{x}\in \mathrm{N}$.

+ Nếu x biểu thị tuổi, sản phẩm, người thì x nguyên dương.

+ Nếu x biểu thị vận tốc của chuyển động thì x > 0.

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Cho một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được một số lớn hơn số đã cho là 63. Tổng của số đã cho và số mới tạo thành bằng 99. Tổng các chữ số của số đó là

A. 9

B. 10

C. 11

D. 12

Lời giải:

Chọn đáp án A

Câu 2: Cho một số có hai chữ số. Chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5. Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng 3/8 số ban đầu. Tìm tích các chữ số của số ban đầu.

A. 12

B. 16

C. 14

D. 6

Lời giải:

Chọn đáp án C

Câu 3: Một ô tô đi quãng đường AB với vận tốc 50 km/h , rồi đi tiếp quãng đường BC với vận tốc 45 km/h . Biết quãng đường tổng cộng dài 165 km và thời gian ô tô đi trên quãng đường AB ít hơn thời gian đi trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên đoạn đường AB.

A. 2 giờ

B. 1,5 giờ

C. 1 giờ

D. 3 giờ

Lời giải:

Gọi thời gian ô tô đi trên mỗi đoạn đường AB và BC lần lượt là x; y

(x > 0; y > 0,5; đơn vị: giờ ) .

Vậy thời gian ô tô đi trên quãng đường AB là 1,5 giờ . Thời gian ô tô đi hết quãng đường BC là 2 giờ.

Chọn đáp án B

Câu 4: Trên một cánh đồng cấy 60 ha lúa giống mới và 40 ha lúa giống cũ, thu hoạch được tất cả 460 tấn thóc. Hỏi năng suất lúa mới trên 1 ha là bằng bao nhiêu, biết rằng 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 1 tấn

A. 5 tấn

B. 4 tấn

C. 6 tấn

D. 3 tấn

Lời giải:

Gọi năng suất lúa mới và lúa cũ trên 1 ha lần lượt là x; y (x, y > 0) đơn vị : tấn/ha

Cấy 60ha lúa giống mới thu hoạch được: 60x (tấn).

Cấy 40ha lúa giống cũ thu hoạch được 40y (tấn)

Vì cấy 60 ha lúa giống mới và 40 ha lúa giống cũ, thu hoạch được tất cả 460 tấn thóc nên ta có

60x + 40y = 460

Vì 3 ha trồng lúa mới thu hoạch được ít hơn 4 ha trồng lúa cũ là 1 tấn nên ta có phương trình

4y - 3x = 1

Suy ra ta có hệ phương trình:

Vậy năng suất lúa mới trên 1 ha là 5 tấn

Chọn đáp án A

Câu 5: Một ô tô dự định đi từ A đến B trong một thời gian nhất định . Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 3 giờ , còn nếu xe chạy chậm lại mỗi giờ 10km thì đến nơi chậm mất 5 giờ. Tính vận tốc của xe lúc ban đầu

A. 40 km/h

B. 35 km/h

C. 50 km/h

D. 60 km/h

Lời giải:

Gọi vận tốc ban đầu là x (km/h); (x > 10). Thời gian chạy dự định là y (giờ)

Chiều dài quãng đường là: x.y

Nếu xe chạy mỗi giờ nhanh hơn 10 km thì đến nơi sớm hơn dự định 3 giờ. Vận tốc xe khi đó là

x + 10 (km /h ); thời gian đi là : y – 3 ( giờ) .

Chiều dài quãng đường là (x + 10)(y - 3)

Nếu xe chạy chậm lại mỗi giờ 10km thì đến nơi chậm mất 5 giờ. Vận tốc xe đi khi đó là: x – 10 ( km/h) và thời gian đi là : y + 5( giờ).

Chiều dài quãng đường là

Suy ra ta có hệ:

Vậy vận tốc ban đầu là 40 km/h

Chọn đáp án A

Câu 6: Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì họ làm được một phần tư công việ

C. Hỏi mỗi người thợ làm một mình thì trong bao nhiêu giờ mới xong công việc đó.

A. 24 giờ và 48 giờ

B. 24 giờ và 36 giờ

C. 36 giờ và 40 giờ

D. Đáp án khác

Lời giải:

Gọi thời gian người thợ thứ nhất làm một mình xong việc là x(giờ) (x > 16)

Thời gian người thợ thứ hai làm một mình xong việc là y(giờ) (y > 16)

Suy ra trong thời gian 1 giờ người thợ thứ nhất làm được 1/x công việc

Trong thời gian 3 giờ người thợ thứ nhất làm được 3/x công việc

Trong thời gian 1 giờ người thợ thứ hai làm được 1/y công việc

Trong thời gian 6 giờ người thợ thứ hai làm được 6/y công việc

Hai người cùng làm trong 16 giờ thì xong việc, nên 1 giờ cả 2 người làm được 1/16 ta có phương trình:

Người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì được một phần tư công việc, ta có phương trình:

Từ đó ta có hệ phương trình:

Kết luận: thời gian người thợ thứ nhất làm một mình xong việc là 24 (giờ)

Thời gian người thợ thứ hai làm một mình xong việc là 48 giờ

Chọn đáp án A.

Câu 7: Hai lớp 9A và 9B có tổng số 82 học sinh. Trong dịp tết trồng cây năm 2020, mỗi học sinh lớp 9A trồng được 3 cây, mỗi học sinh lớp 9B trồng được 4 cây nên cả hai lớp trồng được tổng số 288 cây. Tính số học sinh mỗi lớp.

A. 36 và 46

B. 40 và 42

C. 41 và 41

D. 38 và 44

Lời giải:

Gọi x, y lần lượt là số học sinh của lớp 9A và lớp 9B (x, y ∈ N*; x, y < 82)

Tổng số học sinh của hai lớp là 82 ⇒ x + y = 82 (1)

Mỗi học sinh lớp 9A và 9B lần lượt trồng được 3 cây và 4 cây nên tổng số cây hai lớp trồng là 3x + 4y (cây). Theo bài ra ta có 3x + 4y = 288 (2)

Từ (1) và (2) ta có hệ phương trình:

(thỏa mãn)

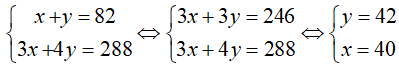
Vậy số học sinh lớp 9A và 9B lần lượt là 40 và 42.

Chọn đáp án B.

Câu 8: Một ô tô và một xe máy ở hai địa điểm A và B cách nhau 180 km, khởi hành cùng một lúc đi ngược chiều nhau và gặp nhau sau 2 giờ. Biết vận tốc của ô tô lớn hơn vận tốc của xe máy 10 km/h. Tính vận tốc của ô tô và xe máy lần lượt là?

A. 40 km/h và 30 km /h

B. 45km/h và 35 km/ h

C. 48km/h và 38km/h

D. 50km/h và 40km/h

Lời giải:

Gọi vận tốc của ô tô là x (km/h)

Vận tốc của xe máy là y (km/h) ( Điều kiện: x > y > 0, x > 10)

Ta có vận tốc của ô tô lớn hơn vận tốc của xe máy 10 km/h nên : x – y = 10 (1)

Sau 2 giờ ô tô đi được quãng đường là 2x (km)

Sau 2 giờ xe máy đi được quãng đường là: 2y (km)

Sau 2 giờ thì chúng gặp nhau, ta có phương trình: 2x + 2y = 180 hay x + y = 90 (2)

Từ (1), (2) ta có hệ phương trình :

Thỏa mãn điều kiện,vậy vận tốc của ô tô là 50 km/h và vận tốc của xe máy là: 40 km/h

Chọn đáp án D.

Câu 9: Hai ô tô cùng khởi hành 1 lúc từ 2 tỉnh A và B cách nhau 400 km đi ngược chiều và gặp nhau sau 5h. Nếu vận tốc của mỗi xe vẫn không thay đổi nhưng xe đi chậm xuất phát trước xe kia 40 phút thì 2 xe gặp nhau sau 5h 22 phút kể từ lúc xe chậm khởi hành. Tính vận tốc của mỗi xe.

A. 44km/ h và 36 km/ h

B. 48km/ h và 32 km/ h

C. 45km/h và 35km/h

D. Đáp án khác

Lời giải:

Gọi vận tốc của xe nhanh là x km/h

Gọi vận tốc của xe chậm là y km/h (điều kiện: x> y > 0)

Hai xe cùng khởi hành một lúc và đi ngược chiều sau 5h gặp nhau nên ta có phương trình

Vậy vận tốc của xe nhanh là 44 km/h

Vận tốc của xe chậm là 36 km/h.

Chọn đáp án A.

Câu 10: Hai người cùng làm một công việc trong 7h 12 phút thì xong công việc nếu người thứ 1 làm trong 4h người thứ 2 làm trong 3h thì được 50% công việ

C. Hỏi mỗi người làm một mình trong mấy giờ thì xong.

A. 10 giờ và 12 giờ

B. 12 giờ và 18 giờ

C. 12 giờ và 16 giờ

D. 10 giờ và 15 giờ

Lời giải:

Gọi thời gian người thứ 1 làm một mình xong công việc là x (giờ), (điều kiện x > 0.

Gọi thời gian người thứ 2 làm một mình xong việc là y (giờ), ( điều kiện y > 0).

Vậy thời gian người thứ 1 làm một mình xong công việc là 12 giờ

Thời gian người thứ 2 làm một mình xong công việc là 18 giờ.

Chọn đáp án B.

II. Bài tập tự luận có lời giải

Câu 1: Tìm số tự nhiên có hai chữ số biết chữ số hàng trục hơn chữ số hàng đơn vị hai đơn vị là 2, nếu viết xen giữa chữ số 0 vào giữa chữ số hàng chục và chữ số hàng đơn vị thì số đó tăng thêm 630 đơn vị.

Lời giải:

Gọi số cần tìm là $\overline{\mathrm{ab}} \left(2\le \mathrm{a}\le 9; 0\le \mathrm{b}\le 9; \mathrm{a},\mathrm{b}\in \mathrm{N}\right)$

Ta có:

$\overline{\mathrm{ab}}=10\mathrm{a}+\mathrm{b}$

Vì chữ số hàng chục hơn chữ số hàng đơn vị hai đơn vị nên ta có phương trình $\mathrm{a}-\mathrm{b}=2$.

Nếu viết xen giữa chữ số 0 vào giữa chữ số hàng chục và chữ số hàng đơn vị thì ta được số mới là $\overline{\mathrm{a}0\mathrm{b}}$

Ta có:

$\overline{\mathrm{a}0\mathrm{b}}=100\mathrm{a}+\mathrm{b}$

Vì số mới lớn hơn số cũ 630 đơn vị nên ta có:

$$\begin{gathered} \overline{\mathrm{a}0\mathrm{b}}-\overline{\mathrm{ab}}=\left(100\mathrm{a}+\mathrm{b}\right)-\left(10\mathrm{a}+\mathrm{b}\right)=630 \\ \iff 100\mathrm{a}+\mathrm{b}-10\mathrm{a}-\mathrm{b}=630 \\ \iff 90\mathrm{a}=630 \\ \iff \mathrm{a}=630:90 \\ \iff \mathrm{a}=7 \mathrm{mà} \mathrm{a}-\mathrm{b}=2 \\ \Rightarrow \mathrm{b}=5 \end{gathered}$$

Vậy số có hai chữ số cần tìm là 75.

Câu 2: Một chiếc xe tải đi từ TP. Hồ Chí Minh đến Tp. Cần Thơ, quãng đường dài 189 km. Sau khi xe tải xuất phát được 1 giờ, một chiếc xe khách bắt đầu đi từ TP. Cần Thơ về Tp. Hồ Chí Minh và gặp xe tải sau khi đã đi được 1 giờ 48 phút. Tính vận tốc mỗi xe, biết rằng mỗi giờ xe khách đi nhanh hơn xe tải 13km.

Lời giải:

Từ giả thuyết bài toán, ta thấy khi hai xe gặp nhau thì

Thời gian xe khách đã đi là 1 giờ 48 phút, tức $\frac{9}{5}$giờ.

Thời gian xe tải đã đi là 1 giờ + $\frac{9}{5}$giờ = $\frac{14}{5}$giờ (vì xe tải khởi hành trước xe khách 1 giờ).

Gọi vận tốc xe tải là x (km/h) và vận tốc của xe khách là y (km/h) (x, y > 0)

Mỗi giờ xe khách đi nhanh hơn xe tải là 13 km nên ta có phương trình

y - x = 13 ⇔ y = 13 + x (1)

Quãng đường xe khách đi được đến khi gặp nhau là: $\frac{9}{5}$y (km)

Quãng đường xe tải đi được đến khi gặp nhau là: $\frac{14}{5}$x (km)

Theo giả thiết quãng đường từ TP. Hồ Chí Minh đến TP. Cần Thơ dài 189 km nên ta có phương trình

$\frac{14}{5}\mathrm{x}+\frac{9}{5}\mathrm{y}=189$ (2)

Từ (1) và (2) ta có hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{l}\mathrm{y}=13+\mathrm{x}\\ \frac{14}{5}\mathrm{x}+\frac{9}{5}\mathrm{y}=189\end{array}\iff \left\{\begin{array}{l}\mathrm{y}=13+\mathrm{x}\\ \frac{14}{5}\mathrm{x}+\frac{9}{5}\left(13+\mathrm{x}\right)=189\end{array}\right.\right. \\ \iff \left\{\begin{array}{l}\mathrm{y}=13+\mathrm{x}\\ \frac{14}{5}\mathrm{x}+\frac{9}{5}\mathrm{y}+\frac{117}{5}=189\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{y}=13+\mathrm{x}\\ \frac{23}{5}\mathrm{x}=189-\frac{117}{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{y}=13+\mathrm{x}\\ \frac{23}{5}\mathrm{x}=\frac{828}{5}\end{array}\iff \left\{\begin{array}{l}\mathrm{y}=13+\mathrm{x}\\ \mathrm{x}=36\end{array}\right.\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=36\\ \mathrm{y}=49\end{array}\left(\mathrm{thỏa} \mathrm{mãn}\right)\right. \end{gathered}$$

Vậy vận tốc của xe tải là 36 km/h

Vận tốc của xe khách là 49 km/h

Câu 3: Hai trường có tất cả 300 học sinh tham gia một cuộc thi. Biết trường A có 75% học sinh đạt, trường 2 có 60% đạt nên cả 2 trường có 207 học sinh đạt. Số học sinh dự thi của trường A và trường B lần lượt là:

Lời giải:

Gọi số học sinh của trường thứ nhất dự thi là x (học sinh) (x ∈ N*, x < 300)

Số học sinh của trường thứ hai dự thi là y (học sinh) (y ∈ N*, y < 300)

Hai trường có tất cả 300 học sinh tham gia cuộc thi nên ta có phương trình: x + y = 300  (1)

Trường A có 75% học sinh đạt, trường 2 có 60% đạt nên cả 2 trường có 207 học sinh đạt, ta có: 

Vậy số học sinh của trường thứ nhất dự thi là 180 học sinh; Số học sinh của trường thứ hai dự thi là 120 học sinh.

Câu 4: Một mảnh đất hình chữ nhật có chu vi bằng 42m. Đường chéo hình chữ nhật dài 15m. Tính độ dài chiều rộng mảnh đất hình chữ nhật.

Lời giải:

Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là: x, y

(21 > x > y > 0; m)

Vì mảnh đất hình chữ nhật có chu vi bằng 42m nên ta có (x + y). 2 = 42

Đường chéo hình chữ nhật dài 15m nên ta có phương trình: x2 + y2 = 152

Vậy chiều rộng mảnh đất ban đầu là 9m

Câu 5: Một mảnh đất hình chữ nhật có nửa chu vi bằng 34 m. Đường chéo hình chữ nhật dài 26 m. Tính chiều dài mảnh đất hình chữ nhật.

Lời giải:

Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là: x, y

(34 > x > y > 0; m)

Vì mảnh đất hình chữ nhật có nửa chu vi bằng 37m nên ta có x + y = 37

Đường chéo hình chữ nhật dài 26m nên ta có phương trình: x2 + y2 = 262

Vậy chiều dài mảnh đất ban đầu là 24m

Câu 6: Hai vòi nước cùng chảy vào một bể thì sau 4 giờ 48 phút bể đầy. Nếu vòi I chảy riêng trong 4 giờ, vòi II chảy riêng trong 3 giờ thì cả hai vòi chảy được 3/4 bể. Tính thời gian vòi I chảy 1 mình đầy bể.

Lời giải:

Gọi thời gian vòi I, vòi II chảy một mình đầy bể lần lượt là x, y 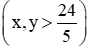 (đơn vị: giờ)

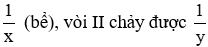
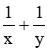
Mỗi giờ vòi I chảy được   bể nên cả hai vòi chảy được  bể

Vì hai vòi ngước cùng chảy vào một bể thì sau 4 giờ 48 phút 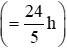  bể đầy nên ta có phương trình: 

Nếu vòi I chảy riêng trong 4 giờ, vòi II chảy riêng trong 3 giờ thì cả hai vòi chảy được 

Suy ra hệ phương trình:

Vậy thời gian vòi I một mình đầy bể là 8h.

Câu 7: Hai vòi ngước cùng chảy vào một bể không có nước thì sau 1,5 giờ sẽ đầy bể. Nếu mở vòi 1 chảy trong 0,25 giờ rồi khóa lại và mở vòi 2 chảy trong 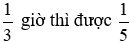 bể. Hỏi nếu vòi 2 chảy riêng thì bao lâu đầy bể?

Lời giải:

Gọi thời gian vòi 1 chảy một mình đầy bể là x (h), thời gian vòi 2 chảy một mình đầy bể là y (h) (x; y > 1,5)

Mỗi giờ vòi I chảy được '  bể nên cả hai vòi chảy được  bể

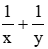
Hai vòi cùng chảy thì sau 1,5h sẽ đầy bể nên ta có phương trình: 

Nếu mở vòi 1 chảy trong 0,25h rồi khóa lại và mở vòi 2 chảy trong 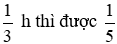 bể nên ta có phương trình  

Từ (1) và (2) ta có hệ phương trình:

Vậy thời gian vòi 2 chảy một mình đầy bể là 2,5h

Câu 8: Một người đi xe đạp từ A đến B cách nhau 24km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4km/h so với lúc đi, nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A đến B.

Lời giải:

Đổi 30 phút = 1/2 giờ.

Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x > 0 ). Thời gian xe đi từ A đến B là 24/x (giờ).

Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là Lý thuyết Giải bài toán bằng cách lập hệ phương trình - Lý thuyết Toán lớp 9 đầy đủ nhất (giờ)

Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:

Giải phương trình:

Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.

Câu 9: Cho một bể cạn (không có nước). Nếu hai vòi nước cùng được mở để chảy vào bể này thì sẽ đầy bể sau 4 giờ 48 phút. Nếu mở riêng từng vòi chảy vào bể thì thời gian vòi một chảy đầy bể sẽ ít hơn thời gian vòi hai chảy đầy bể là 4 giờ. Hỏi mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể?

Lời giải:

Đổi 4 giờ 48 phút

Cách 1: Lập hệ phương trình

Gọi thời gian vòi một chảy một mình đầy bể trong x (giờ, x > 24/5 )

Gọi thời gian vòi hai chảy một mình đầy bể trong y (giờ, y > 24/5 )

Biết hai vòi cùng chảy thì sau 24/5 giờ thì đầy bể nên ta có phương trình: 

Nếu chảy riêng thì vòi một chảy đầy bể nhanh hơn vòi hai là 4 giờ nên ta có phương trình:

     x = y - 4     (2)

Từ (1) và (2) ta có hệ phương trình:

Vậy vòi một chảy một mình trong 8 giờ thì đầy bể và vòi hai chảy một mình trong 12 giờ thì đầy bể.

Câu 10: Tổng của hai số bằng 59. Hai lần của số này bé hơn ba lần của số kia là 7. Tìm hai số đó.

Lời giải:

Gọi x, y là hai số cần tìm.

Vì tổng của hai số bằng 59 nên ta có phương trình: x + y = 59

Vì hai lần của số này bé hơn ba lần của số kia là 7 nên ta có phương trình: 3y – 2x = 7.

Ta có hệ phương trình: $\left\{\begin{array}{l}x+y=59\\ 3y-2x=7\end{array}\right.\iff \left\{\begin{array}{l}2x+2y=118\\ 3y-2x=7\end{array}\right.$

$\iff \left\{\begin{array}{l}2x+2y=118\\ \left(2x+2y\right)+\left(3y-2x\right)=118+7\end{array}\right.$

$\iff \left\{\begin{array}{l}2x+2y=118\\ 5y=125\end{array}\right.\iff \left\{\begin{array}{l}2x+2y=118\\ y=25\end{array}\right.$

$\iff \left\{\begin{array}{l}2x+2.25=118\\ y=25\end{array}\right.$

$\iff \left\{\begin{array}{l}2x=68\\ y=25\end{array}\right.\iff \left\{\begin{array}{l}x=34\\ y=25\end{array}\right.$

Vậy hai số cần tìm là 34 và 25.

III. Bài tập vận dụng

Câu 1: Đem một số có hai chữ số nhân với tổng của các chữ số với nhau thì được kết quả là 405. Nếu viết ngược lại bằng cách như vậy thì tích nhận được là 468. Tìm số đó?

Câu 2: Cho tam giác vuông, biết rằng nếu tăng mỗi cạnh góc vuông lên 2cm thì diện tích tăng 17 cm2. Nếu giảm lần lượt các cạnh góc vuông, một cạnh 3cm, một cạnh 1cm thì diện tích giảm đi 11 cm2 . Tính các cạnh của tam giác vuông ấy

Câu 3: Một ô tô đi quãng đường AB với vận tốc 50 km/h, rồi đi tiếp quãng đường BC với vận tốc 45 km/h. Biết quãng đường tổng cộng dài 165 km và thời gian ô tô đi trên quãng đường AB ít hơn thời gian đi trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên đoạn đường AB.

Câu 4: Một hình chữ nhật có chu vi 300cm. Nếu tăng chiều rộng thêm 5cm và giảm chiều dài 5 cm thì diện tích tăng 275 cm². Tính chiều dài và chiều rộng của hình chữ nhật.

Câu 5: Một ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10 km thì đến nơi sớm hơn dự định 3 giờ, còn nếu xe chạy chậm lại mỗi giờ 10 km thì đến nơi chậm mất 5 giờ. Tính vận tốc của xe lúc ban đầu.

Câu 6: Hai bạn A và B cùng làm chung một công việc thì hoàn thành sau 6 ngày. Hỏi nếu A làm một nửa công việc rồi nghỉ thì B hoàn thành nốt công việc trong bao lâu? Biết rằng nếu làm một mình xong công việc thì B làm lâu hơn A là 9 ngày.

Câu 7: Hai giá sách có 450 cuốn. Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng  số sách ở giá thứ nhất. Tính số sách trên giá thứ hai.

Câu 8: Trên một cánh đồng cấy 50 ha lúa giống mới và 30 ha lúa giống cũ, thu hoạch được tất cả 410 tấn thóc. Hỏi năng suất lúa cũ trên 1 ha là bao nhiêu, biết rằng 5 ha trồng lúa mới thu hoạch được nhiều hơn 6 ha trồng lúa cũ là 0,5 tấn.

Câu 9: Một cano chạy trên  sông trong 7 giờ, xuôi dòng 108 km và ngược dòng 63 km. Một lần khác cũng trong 7 giờ, cano xuôi dòng 81 km và ngược dòng 84 km. Tính vận tốc nước chảy.

Câu 10: Một tam giác có chiều cao bằng  cạnh đáy. Nếu chiều cao tăng thêm 3 dm và cạnh đáy giảm đi 4 dm thì diện tích của nó tăng thêm 12 dm². Tính diện tích của tam giác ban đầu.

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Ôn tập chương 3

Chuyên đề Hàm số y = ax^2 (a khác 0)

Chuyên đề Đồ thị của hàm số y = ax^2 (a khác 0)

Chuyên đề Phương trình bậc hai một ẩn

Chuyên đề Công thức nghiệm của phương trình bậc hai