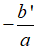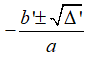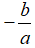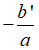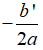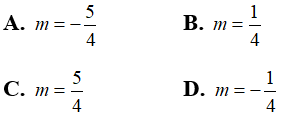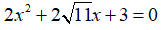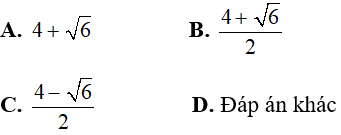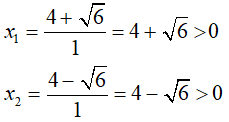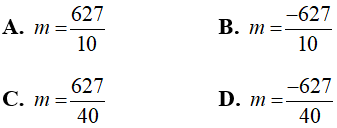Chuyên đề Công thức nghiệm thu gọn (2022) - Toán 9

Chuyên đề Công thức nghiệm thu gọn - Toán 9

A. Lý thuyết

1. Công thức nghiệm thu gọn

a) Biệt thức $∆\text{'}$

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) và b = 2b’ ta có biệt thức  như sau:

$∆\text{'}$= $\mathrm{b}{\text{'}}^2-\mathrm{ac}$

Ta sửa dụng biết thức $∆\text{'}$để giải phương trình bậc hai.

b) Công thức nghiệm thu gọn của phương trình bậc hai

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) có b = 2b’ và biệt thức $∆\text{'}$= b’² - ac

+ Nếu  > 0 thì phương trình có hai nghiệm phân biệt là

${\mathrm{x}}_1=\frac{-\mathrm{b}+\sqrt{∆\text{'}}}{\mathrm{a}}; {\mathrm{x}}_2=\frac{-\mathrm{b}+\sqrt{∆\text{'}}}{\mathrm{a}}$

+ Nếu  = 0 thì phương trình có nghiệm kép là

${\mathrm{x}}_1={\mathrm{x}}_2=\frac{-\mathrm{b}}{\mathrm{a}}$

+ Nếu  < 0 thì phương trình vô nghiệm.

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac. Phương trình đã cho có hai nghiệm phân biệt khi:

A. Δ' > 0

B. Δ' = 0

C. Δ' ≥ 0

D. Δ' ≤ 0

Lời giải:

Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac:

• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm

• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép x1 = x2 = 

• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt x1,2 = 

Chọn đáp án A.

Câu 2: Cho phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac. Nếu Δ' = 0 thì:

A. Phương trình có hai nghiệm phân biệt

B. Phương trình có nghiệm kép x1 = x2 = 

C. Phương trình có nghiệm kép x1 = x2 = 

D. Phương trình có nghiệm kép x1 = x2 = 

Lời giải:

Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b'2 - ac:

Nếu Δ' = 0 thì phương trình có nghiệm kép x1 = x2 = 

Chọn đáp án C.

Câu 3: Tính Δ' và tìm số nghiệm của phương trình 7x2 - 12x + 4 = 0

A. Δ' = 6 và phương trình có hai nghiệm phân biệt

B. Δ' = 8 và phương trình có hai nghiệm phân biệt

C. Δ' = 8 và phương trình có nghiệm kép

D. Δ' = 0 và phương trình có hai nghiệm phân biệt

Lời giải:

Phương trình 7x2 - 12x + 4 = 0 có a = 7; b' = -6; c = 4 suy ra:

Δ' = (b')2 - ac = (-6)2 - 4.7 = 8 > 0

Nên phương trình có hai nghiệm phân biệt.

Chọn đáp án B.

Câu 4: Tìm m để phương trình 2mx2 - (2m + 1)x - 3 = 0 có nghiệm là x =2

Lời giải:

Chọn đáp án C.

Câu 5: Tính Δ' và tìm nghiệm của phương trình 

Lời giải:

Chọn đáp án D.

Câu 6: Tìm nghiệm dương của phương trình: x2 - 8x + 10 = 0

Lời giải:

Ta có: a = 1; b = - 8 nên b’ = -4; c = 10.

Δ' = (-4)2 - 1.10 = 16 - 10 = 6

Do đó, phương trình đã cho có hai nghiệm phân biệt là;

Vậy cả hai nghiệm trên đều là nghiệm dương của phương trình đã cho.

Chọn đáp án D.

Câu 7: Cho phương trình 2x2 - 10x + m + 1 = 0; ( m là tham số). Tìm m để biệt thức Δ' = 11

A. m = 3

B. m = 6

C. m = 9

D. m = -2

Lời giải:

Ta có: a = 2 ; b = -10 nên b’ = -5; c = m + 1

Δ' = (-5)2 - 2.(m + 1) = 25 - 2m - 2 = 23 - 2m

Để Δ' = 11 thì 23 – 2m = 11

⇔ -2m = -12 ⇔ m = 6

Chọn đáp án B.

Câu 8: Cho phương trình 2x2 – 4x + m = 0. Tìm m để phương trình trên vô nghiệm?

A. m < 3

B. m > - 3

C. m > 2

D. m < -2

Lời giải:

Ta có: a = 2; b = - 4 nên b’ = -2 và c = m

Δ' = (-2)2 - 2m = 4 - 2m

Để phương trình đã cho vô nghiệm thì:4 – 2m < 0 hay m > 2 .

Chọn đáp án C.

Câu 9: Cho hai phương trình x2 – 4x + 4= 0 và x2 + (m + 1)x + m = 0 . Tìm m để hai phương trình trên có nghiệm chung?

A. m = 2 hoặc m = -1

B. m = 1 hoặc m = 2

C. m = -1

D. m = -2

Lời giải:

* Xét phương trình : x2 – 4x + 4= 0

⇔ (x-2)2 = 0 ⇔ x - 2 = 0 ⇔ x = 2

Vậy phương trình này có nghiệm duy nhất.

Để hai phương trình đã cho có nghiệm chung khi và chỉ khi x = 2 là nghiệm phương trình

x2 + (m + 1)x + m = 0.Suy ra:

22 + (m + 1).2 + m = 0

⇔ 4 + 2m + 2 + m = 0 ⇔ 6 + 3m = 0

⇔ 3m = +6 ⇔ m = -2

Chọn đáp án D.

Câu 10: Cho phương trình: -8x2 + 100x + 40m = 0. Tìm m để phương trình trên có nghiệm duy nhất?

Lời giải:

Chọn đáp án B.

II. Bài tập tự luận có lời giải

Câu 1: Giải phương trình bậc hai 

Lời giải:

Cách 1: Xét phương trình  có

Ta có:

Do ∆’ > 0 nên phương trình có hai nghiệm phân biệt

Cách 2: Nhẩm nghiệm

Ta có: a + b + c = 

=> Phương trình có hai nghiệm phân biệt

Câu 2: Xác định có hệ số a, b, b’, c rồi tính biệt thức $∆\text{'}$của các phương trình sau:

a) ${\mathrm{x}}^2+6\mathrm{x}-3=0$

b) $2{\mathrm{x}}^2+2\mathrm{x}+6=0$

c) $4{\mathrm{x}}^2+4\mathrm{x}+1=0$

Lời giải:

a) ${\mathrm{x}}^2+6\mathrm{x}-3=0$

Có a = 1; b = 6; b’ = 3; c = -3

$∆\text{'}=\mathrm{b}{\text{'}}^2-\mathrm{ac}=3^2-1.\left(-3\right)=12$

b) $2{\mathrm{x}}^2+2\mathrm{x}+6=0$

Có a = 2; b = 2; b’ = 1; c = 6

$∆\text{'}=\mathrm{b}{\text{'}}^2-\mathrm{ac}=1^2-2.6=1-12=-11$

c) $4{\mathrm{x}}^2+4\mathrm{x}+1=0$

Có a = 4; b = 4; b’ = 2; c = 1.

$∆\text{'}=\mathrm{b}{\text{'}}^2-\mathrm{ac}=2-4.1=4-4=0$

Câu 3: Giải các phương trình sau:

a) $3{\mathrm{x}}^2+8\mathrm{x}-5=0$

b) $2{\mathrm{x}}^2+4\mathrm{a}+7=0$

Lời giải:

a) $3{\mathrm{x}}^2+8\mathrm{x}-5=0$

Ta có: a = 3; b = 8; b’ = 4; c = -5

$∆\text{'}=\mathrm{b}{\text{'}}^2-\mathrm{ac}=4^2-3.\left(-5\right)=16+15=31>0$

Phương trình đã cho có hai nghiệm phân biệt

${\mathrm{x}}_1=\frac{-\mathrm{b}+\sqrt{∆\text{'}}}{\mathrm{a}}=\frac{-4+\sqrt{31}}{3}$;

${\mathrm{x}}_2=\frac{-\mathrm{b}\text{'}-\sqrt{∆\text{'}}}{\mathrm{a}}=\frac{-4-\sqrt{31}}{3}$.

Vậy phương trình đã cho có hai nghiệm phân biệt $\mathrm{S}=\left\{\frac{-4+\sqrt{31}}{3}; \frac{-4-\sqrt{31}}{3}\right\}$

b) $2{\mathrm{x}}^2+4\mathrm{a}+7=0$

Ta có: a = 2; b = 4; b’ = 2; c = 7

$∆=\mathrm{b}{\text{'}}^2-\mathrm{ac}=2^2-2.7=4-14=-10<0$

Phương trình vô nghiệm.

Câu 4: Cho phương trình ${\mathrm{x}}^2+2\left(\mathrm{m}+3\right)\mathrm{x}+{\mathrm{m}}^2-3\mathrm{m}=0$

a) Tính $∆\text{'}$

b) Với giá trị nào của m thì phương trình vô nghiệm? Vô số nghiệm? Có nghiệm kép?

Lời giải:

a) Ta có: a = 1; b = 2(m + 3); b’ = m + 3; c = m² – 3m

$\mathrm{∆\text{'}=}{\left(\mathrm{m}+3\right)}^2-1.\left({\mathrm{m}}^2-3\mathrm{m}\right)={\mathrm{m}}^2+6\mathrm{m}+9-{\mathrm{m}}^2+3\mathrm{m}=9\mathrm{m}+9$

b) Ta có a = 1$\ne 0$

 + Để phương trình vô nghiệm thì:

$∆\text{'}<0\Rightarrow 9\mathrm{m}+9<0\iff 9\mathrm{m}<-9\iff \mathrm{m}<-1$

+ Để phương trình có hai nghiệm phân biệt thì:

$∆\text{'}>0\Rightarrow 9\mathrm{m}+9>0\iff 9\mathrm{m}>-9\iff \mathrm{m}>-1$

+ Để phương trình nghiệm kép thì:

$∆\text{'}=0\iff 9\mathrm{m}+9=0\iff 9\mathrm{m}=-9\iff \mathrm{m}=-1$

Câu 5: Xác định a, b’,c trong mỗi phương trình rồi giải phương trình bằng công thức nghiệm thu gọn:

a) 5x² – 6x –1 = 0

b) –3x² + 14x – 8 = 0

c) –7x² + 4x = 3

d) 9x² + 6x + 1 = 0

Lời giải:

a) Phương trình 5x² – 6x –1 = 0 có hệ số a = 5, b’ = –3, c = –1

Ta có: Δ’ = b’² – ac = (–3)² –5.(–1) = 9 + 5 = 14 > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{3+\sqrt{14}}{5}$;

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{3-\sqrt{14}}{5}$

Vậy tập nghiệm của phương trình là: $S=\left\{\frac{3+\sqrt{14}}{5};\frac{3-\sqrt{14}}{5}\right\}$

b) Phương trình –3x² + 14x – 8 = 0 có hệ số a = –3, b’= 7, c = –8

Ta có: Δ' = b’² – ac = 7² – (–3).(–8) = 49 – 24 = 25 > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-7+\sqrt{25}}{-3}=\frac{2}{3}$;

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-7-\sqrt{25}}{-3}=4$

Vậy tập nghiệm của phương trình là: $S=\left\{\frac{2}{3};4\right\}$

c) Phương trình –7x² + 4x = 3 ⇔ 7x² – 4x + 3 = 0 có hệ số a=7, b’=–2 , c=3

Ta có: Δ’ = b’² – ac = (–2)² – 7.3 = 4 – 21 = –17 < 0

Vậy phương trình vô nghiệm

d) Phương trình 9x² + 6x + 1 = 0 có hệ số a = 9, b’ = 3, c = 1

Ta có: Δ’ = b’² – ac = 3² – 9.1 = 9 – 9 = 0

Phương trình có nghiệm kép:

x₁ = x₂ = $\frac{-b\text{'}}{a}=\frac{-3}{9}=\frac{-1}{3}$

Vậy tập nghiệm của phương trình là S = $\left\{\frac{-1}{3}\right\}$

Câu 6: Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau?

a) x² + 2 + 2$\sqrt{2}$  và 2(1 + $\sqrt{2}$ )x

b) $\sqrt{3}$ x² + 2x – 1 và 2$\sqrt{3}$ x + 3

c) –2$\sqrt{2}$ x – 1 và $\sqrt{2}$ x² + 2x +3

Lời giải:

a) Ta có: x² +2 + 2$\sqrt{2}$  = 2(1 + $\sqrt{2}$ )x

⇔ x² – 2(1 +$\sqrt{2}$ )x +2 +2$\sqrt{2}$  = 0

Δ' = b’² – ac = [–(1 + $\sqrt{2}$ )]²– 1(2 + 2$\sqrt{2}$ )

= 1 + 2$\sqrt{2}$  + 2 – 2 – 2$\sqrt{2}$  = 1 > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{1+\sqrt{2}+1}{1}=2+\sqrt{2}$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{1+\sqrt{2}-1}{1}=\sqrt{2}$

Vậy với x =$2+\sqrt{2}$  hoặc x =$\sqrt{2}$ thì giá trị của hai biểu thức trên bằng nhau.

b) Ta có: $\sqrt{3}$ x² + 2x – 1 = 2$\sqrt{3}$ x +$\sqrt{3}$

 ⇔ $\sqrt{3}$ x² + 2x – 2$\sqrt{3}$ x – 3 – 1 = 0

⇔ $\sqrt{3}$x² + (2 – 2$\sqrt{3}$ )x – 4 =0

⇔ $\sqrt{3}$ x² + 2(1 – $\sqrt{3}$ )x – 4 = 0

Δ' = b’² – ac = (1– $\sqrt{3}$ )² – $\sqrt{3}$ (–4) =1 – 2$\sqrt{3}$  + 3 + 4$\sqrt{3}$

= 1 + 2$\sqrt{3}$  + 3 = (1 +$\sqrt{3}$ )²> 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-\left(1-\sqrt{3}\right)+\sqrt{{\left(1+\sqrt{3}\right)}^2}}{\sqrt{3}}=\frac{2\sqrt{3}}{\sqrt{3}}=1$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-\left(1-\sqrt{3}\right)-\sqrt{{\left(1+\sqrt{3}\right)}^2}}{\sqrt{3}}=\frac{-2}{\sqrt{3}}=\frac{-2\sqrt{3}}{3}$

Vậy với x = 2 hoặc x = $\frac{-2\sqrt{3}}{3}$  thì giá trị hai biểu thức trên bằng nhau.

c) Ta có: –2$\sqrt{2}$ x – 1 =$\sqrt{2}$ x² + 2x + 3

⇔ $\sqrt{2}$ x² + 2x + 3 + 2$\sqrt{2}$ x + 1=0

⇔ $\sqrt{2}$x² + 2(1 + $\sqrt{2}$ )x + 4 =0

Δ' = b’² – ac= (1+ $\sqrt{2}$ )² – $\sqrt{2}$ .4 = 1 + 2$\sqrt{2}$  + 2 – 4$\sqrt{2}$

= 1 –  2$\sqrt{2}$  + 2 = ($\sqrt{2}$  – 1)² > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-\left(1+\sqrt{2}\right)+\sqrt{{\left(\sqrt{2}-1\right)}^2}}{\sqrt{2}}=\frac{-2}{\sqrt{2}}=-\sqrt{2}$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-\left(1+\sqrt{2}\right)-\sqrt{{\left(\sqrt{2}-1\right)}^2}}{\sqrt{2}}=\frac{-2\sqrt{2}}{\sqrt{2}}=-2$

Vậy với x = $-\sqrt{2}$  hoặc x = -2 thì giá trị của hai biểu thức trên bằng nhau.

Câu 7: Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau?

a) x² – 2$\sqrt{3}$ x – $\sqrt{3}$  và 2x² + 2x + $\sqrt{3}$

b) $\sqrt{3}$ x² + 2$\sqrt{5}$ x – 3$\sqrt{3}$  và –x² – 2$\sqrt{3}$ x +2$\sqrt{5}$ +1

Lời giải:

a) Ta có: x² – 2$\sqrt{3}$ x –  = 2x² + 2x +$\sqrt{3}$

⇔ x² – 2$\sqrt{3}$ x – $\sqrt{3}$  – 2x² – 2x – $\sqrt{3}$  =0

⇔ –x² – 2x – 2$\sqrt{3}$ x – 2$\sqrt{3}$  =0

⇔ x² + 2x + 2$\sqrt{3}$ x + 2$\sqrt{3}$  =0

⇔ x² + 2(1 +$\sqrt{3}$  )x + 2$\sqrt{3}$  =0

Δ' = b’² – ac= (1+$\sqrt{3}$ )² – 1. 2$\sqrt{3}$  = 1 + 2$\sqrt{3}$  + 3 –2$\sqrt{3}$  = 4 > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-\left(1+\sqrt{3}\right)+\sqrt{4}}{1}=1-\sqrt{3}$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-\left(1+\sqrt{3}\right)-\sqrt{4}}{1}=-3-\sqrt{3}$

Vậy với x = $1-\sqrt{3}$  hoặc x = –3 – $\sqrt{3}$  thì giá trị hai biểu thức trên bằng nhau.

b) Ta có: $\sqrt{3}$ x² + 2$\sqrt{5}$ x – 3$\sqrt{3}$  = –x² – 2$\sqrt{3}$ x + 2$\sqrt{5}$  + 1

⇔ $\sqrt{3}$ x² + 2$\sqrt{5}$ x – 3$\sqrt{3}$  + x² + 2$\sqrt{3}$ x – 2$\sqrt{5}$  – 1 = 0

⇔ ($\sqrt{3}$  + 1)x² + (2$\sqrt{5}$  + 2$\sqrt{3}$ )x – 3$\sqrt{3}$  – 2$\sqrt{5}$  – 1 = 0

⇔ ($\sqrt{3}$  +1)x² + 2($\sqrt{5}$  + $\sqrt{3}$ )x – 3$\sqrt{3}$  – 2$\sqrt{5}$  – 1 = 0

Δ' = b’² – ac = ($\sqrt{3}$  + $\sqrt{5}$ )² – ($\sqrt{3}$  + 1)( –3$\sqrt{3}$  – 2$\sqrt{5}$  – 1)

= 5 + 2$\sqrt{15}$ + 3 + 9 + 2$\sqrt{15}$ + $\sqrt{3}$  + 3$\sqrt{3}$  + 2$\sqrt{5}$ + 1

=18 + 4$\sqrt{15}$ + 4$\sqrt{3}$  + 2$\sqrt{5}$

= 1 + 12 + 5 + 2.2$\sqrt{3}$  + 2$\sqrt{5}$  + 2.2$\sqrt{3}$ .$\sqrt{5}$

= 1 + (2$\sqrt{3}$ )² + ($\sqrt{5}$ )² + 2.1.2$\sqrt{3}$  + 2.1.$\sqrt{5}$  + 2.2$\sqrt{3}$ .$\sqrt{5}$

= (1 + 2$\sqrt{3}$  + $\sqrt{5}$ )² > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-\left(\sqrt{5}+\sqrt{3}\right)+\sqrt{{\left(1+2\sqrt{3}+\sqrt{5}\right)}^2}}{\sqrt{3}+1}=1$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-\left(\sqrt{5}+\sqrt{3}\right)-\sqrt{{\left(1+2\sqrt{3}+\sqrt{5}\right)}^2}}{\sqrt{3}+1}=\frac{-1-3\sqrt{3}-2\sqrt{5}}{\sqrt{3}+1}$

Vậy với x = 1 hoặc x = $\frac{-1-3\sqrt{3}-2\sqrt{5}}{\sqrt{3}+1}$  thì giá trị hai biểu thức bằng nhau.

Câu 8: Một vận động viên bơi lội nhảy cầu (xem hình dưới). Khi nhảy, độ cao h từ người đó đến mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức : h = –(x – 1)² + 4 . Hỏi khoảng cách x bằng bao nhiêu:

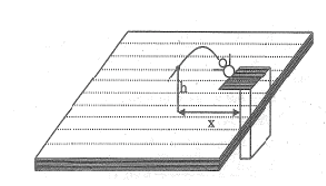
a) Khi vận động viên ở độ cao 3m?

b) Khi vận động viên chạm mặt nước?

Lời giải:

a) Khi vận động viên ở độ cao 3m nghĩa là h = 3m

Ta có: 3 = –(x – 1)² + 4

⇔ (x – 1)² – 4 + 3 = 0

⇔ (x – 1)² – 1 = 0

⇔ x² – 2x + 1 – 1 = 0

⇔ x² – 2x = 0

⇔ x(x – 2) = 0 ⇔ x = 0 hoặc x – 2 = 0 ⇔ x = 0 hoặc x = 2

Vậy x = 0m hoặc x = 2m

b) Khi vận động viên chạm mặt nước nghĩa là h = 0m

Ta có: 0 = – (x – 1)² + 4

⇔ –x² + 2x – 1 + 4 =0

⇔ x² – 2x – 3 =0

Δ' = b’² – ac = (–1)² –1.(–3) =1 +3 = 4 > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b+\sqrt{\Delta \text{'}}}{a}=\frac{-\left(-1\right)+\sqrt{4}}{1}=1+2=3$

$x_2=\frac{-b-\sqrt{\Delta \text{'}}}{a}=\frac{-\left(-1\right)-\sqrt{4}}{1}=1-2=-1$

Vì khoảng cách không thể nhận giá trị âm nên x = 3.

Câu 9: Tính gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai):

a) 16x² – 8x + 1 = 0

b) 6x² – 10x – 1 = 0

c) 5x² + 24x + 9 = 0

d) 16x² – 10x + 1 = 0

Lời giải:

a) 16x² – 8x +1=0

Ta có: Δ' = (–4)² – 16.1 = 16 – 16 =0

Phương trình có nghiệm kép:

$x_1=x_2=\frac{-b\text{'}}{a}=\frac{4}{16}=\frac{1}{4}=0,25$

Vậy tập nghiệm của phương trình là S = {0,25}

b) 6x² – 10x – 1 = 0

Ta có: $\Delta \text{'}={\left(-5\right)}^2-6.\left(-1\right)=25+6=31>0$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-\left(-5\right)+\sqrt{31}}{6}=\frac{5+\sqrt{31}}{6}\approx 1,76$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-\left(-5\right)-\sqrt{31}}{6}=\frac{5-\sqrt{31}}{6}\approx -0,09$

Vậy tập nghiệm của phương trình là S = {1,76;–0,09}

c) 5x² + 24x + 9 = 0

Ta có: Δ' = 12² – 5.9 = 144 – 45 = 99 > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b+\sqrt{\Delta \text{'}}}{a}=\frac{-12+\sqrt{99}}{5}\approx -0,41$

$x_2=\frac{-b-\sqrt{\Delta \text{'}}}{a}=\frac{-12-\sqrt{99}}{5}\approx -4,39$

Vậy tập nghiệm của phương trình là S = {–0,41; –4,39}

d) $16x^2-10x+1=0$

Ta có: $\Delta \text{'}={\left(-5\right)}^2-16.1=25-16=9$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta \text{'}}}{a}=\frac{-\left(-5\right)+\sqrt{9}}{16}=0,5$

$x_2=\frac{-b-\sqrt{\Delta \text{'}}}{a}=\frac{-\left(-5\right)-\sqrt{9}}{16}\approx 0,13$

Vậy tập nghiệm của bất phương trình S = {0,5; 0,13}.

Câu 10: Với giá trị nào của x thì giá trị của hai hàm số bằng nhau?

a)  $y=\frac{1}{3}{x}^2$ và y = 2x – 3

b)  $y=-\frac{1}{2}{x}^2$ và y = x – 8

Lời giải:

a) Ta có: Để giá trị của hai hàm số bằng nhau thì $\frac{1}{3}{x}^2=2x-3$

$\iff \frac{1}{3}{x}^2-2x+3=0$

$\iff x^2-6x+9$

$\Delta \text{'}=b{\text{'}}^2-ac=3^2-9.1=0$

Phương trình có nghiệm kép $x_1=x_2=\frac{-b\text{'}}{a}=\frac{3}{1}=3$

Vậy để giá trị hai hàm số bằng nhau thì x = 3

b) Ta có: $\frac{-1}{2}{x}^2=x-8$

$\iff \frac{-1}{2}{x}^2-x+8=0$

$\iff x^2+2x-16$= 0

$\Delta \text{'}=1^2-1.\left(-16\right)=1+16=17>0$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-1+\sqrt{17}}{1}=-1+\sqrt{17}$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-1-\sqrt{17}}{1}=-1-\sqrt{17}$

Vậy giá trị hai hàm số bằng nhau khi $x=-1+\sqrt{17}$  hoặc $x=-1-\sqrt{17}$ .

III. Bài tập vận dụng

Câu 1: Giải các phương trình :  

a) 4 – 20x + 25 = 0 ;

b) 3 – 4x + 7 = 0 ;

c) 2 – 4x –  = 0.

Câu 2:

Cho phương trình  -2(2m – 1)x – 3m = 0 (1), trong đó m là tham số.

a) Chứng minh rằng phương trình (1) có nghiệm với mọi giá trị của m.

b) Tìm m để phương trình (1) có nghiệm x = -3.

Câu 3: Giải các phương trình:

a) 7 – 6x + 2 = 0;

b) 16 + 24x + 9 = 0.

Câu 4: Giải các phương trình :

a) 4 – 6x – 5 = 0 ;

b)  –  10x  – 24 = 0.

Câu 5: Cho phương trình  – 6x +  – 4m = 0.

a) Tìm m để phương trình có nghiệm x = 1.

b) Tìm m để phương trình có nghiệm kép.

Câu 6: Cho parabol (P): y =  và đường thẳng (d): y = 3mx – 1 – m.

a) Chứng minh đường thẳng (d) luôn đi qua một điểm cố định.

b) Tìm m để đường thẳng (d) tiếp xúc với (P).

Câu 7: Cho phương trình (ẩn x):  – 2(k – 1)x + k – 7 = 0

Chứng minh rằng phương trình luôn luôn có nghiệm với mọi k.

Câu 8: Cho phương trình  – 2mx +  + 3m – 1 = 0.

a) Tìm m để phương trình có nghiệm x = -3.

b) Tìm m để phương trình có nghiệm.

Câu 9: Cho phương trình 4x +  – 12 – 2y + 14 = 0. Chứng minh rằng có duy nhất một cặp số (x ; y) thoả mãn phương trình đã cho.

Câu 10: Giả sử x₁, x₂ là hai nghiệm của phương trình bậc hai ax² + bx + c = 0 có ∆’ = 0. Điều nào sau đây là đúng?

A) $x_1=x_2=\frac{b}{2a}$

B) $x_1=x_2=\frac{-b\text{'}}{a}$

C) $x_1=x_2=\frac{-b}{a}$

D) $x_1=x_2=\frac{-b\text{'}}{2a}$

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Hệ thức Vi – ét và ứng dụng

Chuyên đề Phương trình quy về phương trình bậc hai

Chuyên đề Giải bài toán bằng cách lập phương trình

Chuyên đề Bài tập ôn tập chương

Chuyên đề Góc ở tâm. Số đo cung