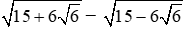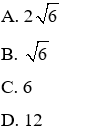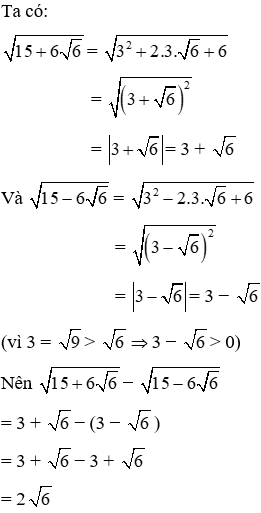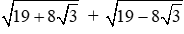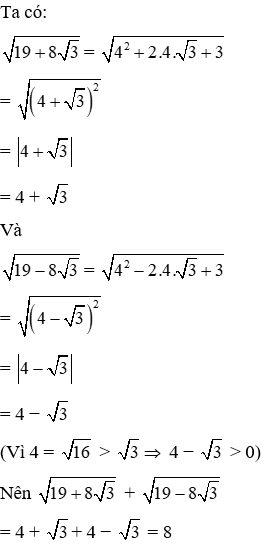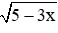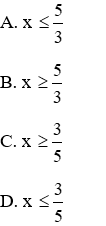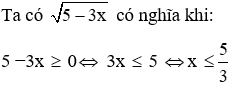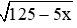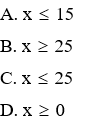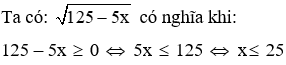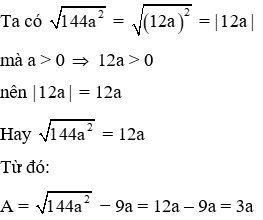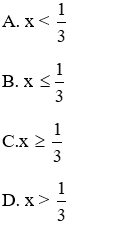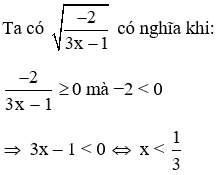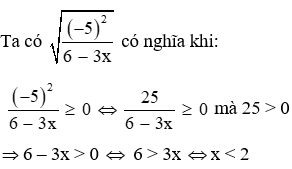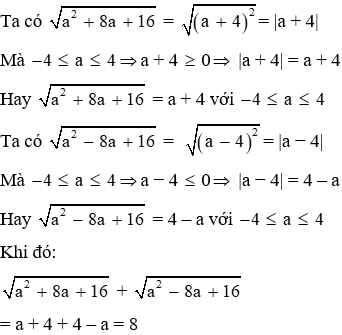Nội dung bài viết

    Xem thêm

    Chuyên đề Căn bậc hai và hằng đẳng thức (2022) - Toán 9

    Với Chuyên đề Căn bậc hai và hằng đẳng thức (2022) - Toán 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.

    1 4,001 27/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Chuyên đề Căn bậc hai và hằng đẳng thức - Toán 9

    A. Lý thuyết

    1. Căn thức bậc hai

    Với A là một biểu thức đại số, người ta gọi A là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.

    A xác định (có nghĩa) khi A lấy giá trị không âm.

    Ví dụ 1. 5x là căn thức bậc hai của 5x;

    5x xác định khi 5x ≥ 0, tức là khi x ≥ 0.

    2. Hằng đẳng thức A2=A

    Định lí. Với mọi số a, ta có a2=a.

    Ví dụ 2. Tính

    a) 142;

    b) (−20)2.

    Lời giải:

    a) 142=14=14.

    b) (− 20)2=− 20=20.

    Chú ý. Một cách tổng quát, với A là một biểu thức ta có A2=A, có nghĩa là:

    A2=A nếu A ≥ 0 (tức là A lấy giá trị không âm);

    A2=− A nếu A < 0 (tức là A lấy giá trị âm).

    Ví dụ 3. Rút gọn

    a) (x−4)2 với x < 4;

    b) a6 với a ≥ 0.

    Lời giải:

    a) (x−4)2=x−4=4−x (vì x < 4);

    b) a6=(a3)2=  |a3|.

    Vì a ≥ 0 nên a3 ≥ 0, do đó | a3 | = a3.

    Vậy a6=a3 (với a ≥ 0).

    B. Bài tập

    I. Bài tập trắc nghiệm

    Câu 1: Tính giá trị biểu thức Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: A

    Câu 2: Tính giá trị biểu thức Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: D

    Câu 3: Tìm điều kiện xác định của Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: A

    Câu 4: Tìm điều kiện xác định của Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: C

    Câu 5: Rút gọn biểu thức 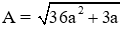Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án  với a > 0

    A. −9a            

    B. −3a            

    C. 3a                           

    D. 9a

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: D

    Câu 6: Rút ngọn biểu thức: 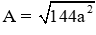Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án với a > 0

    A. −9a            

    B. −3a            

    C. 3a                           

    D. 9a

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: C

    Câu 7: Tìm x để 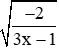Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án có nghĩa

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: A

    Câu 8: Tìm x để 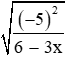Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án có nghĩa

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: A

    Câu 9: Rút gọn biểu thức Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án với -4≤a≤4 ta được

    A. 2a                          

    B. 8                            

    C. −8                          

    D. −2a

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: B

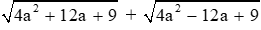
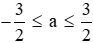
    Câu 10: Rút gọn biểu thức Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án với Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án ta được:

    A. −4a            

    B. 4a                           

    C. −6                          

    D. 6

    Lời giải:

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Trắc nghiệm Căn thức bậc hai và hằng đẳng thức có đáp án

    Đáp án cần chọn là: D

    II. Bài tập tự luận có lời giải

    Câu 1: Với giá trị nào của a thì mỗi căn thức sau có nghĩa:

    a) a4;

    b) − 3a;

    c) 2a+9.

    Lời giải:

    a) Điều kiện xác định: a4≥0⇔a≥0.

    Vậy với a ≥ 0 thì a4 có nghĩa.

    b) Điều kiện xác định: − 3a ≥ 0 ⇔ a ≤ 0.

    Vậy với a ≤ 0 thì − 3a có nghĩa.

    c) Điều kiện xác định: 2a + 9 ≥ 0 ⇔a≥− 92.

    Vậy với a≥− 92 thì 2a+9 có nghĩa.

    Câu 2: Rút gọn các biểu thức sau:

    a) (3−6)2;

    b) 3a2 với a ≥ 0;

    c) 5(a−3)2 với a < 3.

    Lời giải:

    a) (3−6)2=3−6=3−6.

    Ta có 3=9 mà 9>6 nên 3−6>0.

    Do đó 3−6=3−6.

    Vậy (3−6)2=3−6.

    b) 3a2=3a.

    Vì a ≥ 0 nên 3|a| = 3a.

    Vậy 3a2=3a.

    c) 5(a−3)2=5a−3.

    Vì a < 3 nên a – 3 < 0.

    Do đó 5|a – 3| = 5(3 – a) = 15 – 5a.

    Vậy 5(a−3)2=15−5a.

    Câu 3: Tìm x, biết:

    a) x2=15;

    b) 9x2=12;

    c) 16x2=  |−20|.

    Lời giải:

    a) x2=15

    ⇔|x| = 15

    ⇔x = ± 15.

    Vậy x = ± 15.

    b) 9x2=12

    ⇔(3x)2=12

    ⇔|3x| = 12

    ⇔3x = ± 12

    ⇔x = ± 4.

    Vậy x = ± 4.

    d) 16x2=  |−20|

    ⇔(4x)2= 20

    ⇔|4x| = 20

    ⇔4x = ± 20

    ⇔x = ± 5.

    Vậy x = ± 5.

    Câu 4: Rút gọn các biểu thức sau:

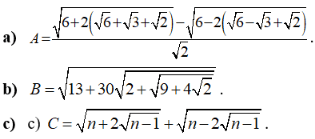
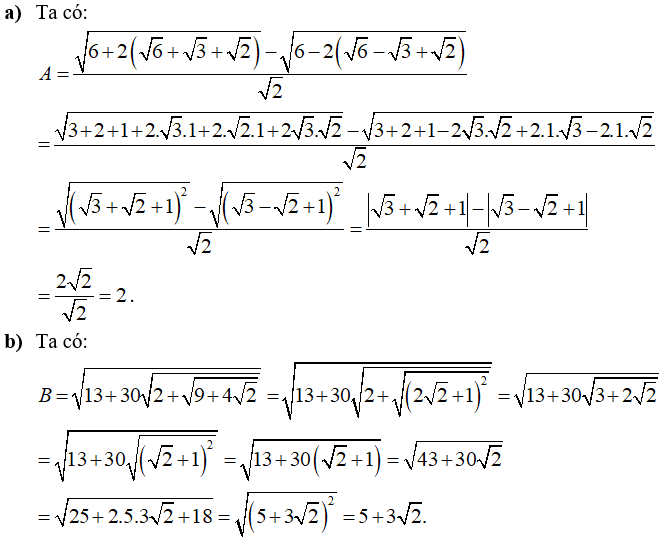
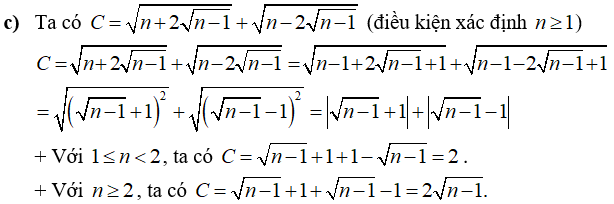
    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Lời giải:

    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Câu 5: Giải các phương trình sau

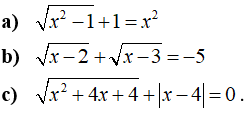
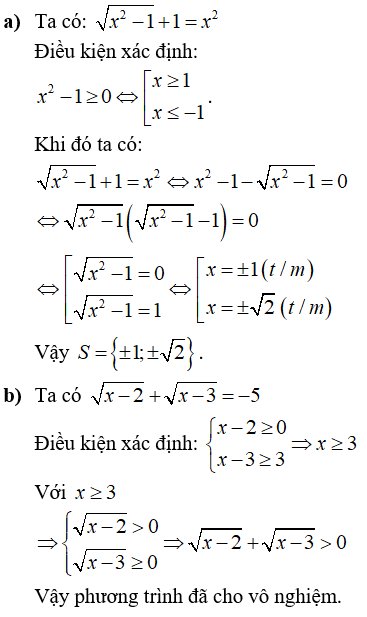
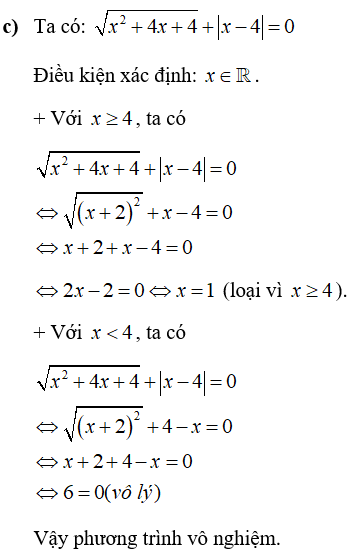
    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Lời giải:

    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Câu 6: Cho biểu thức: Bài tập: Căn thức bậc hai và hằng đẳng thức

    a) Tìm tập xác định của biểu thức.

    b) Rút gọn biểu thức A.

    Lời giải:

    a) Điều kiện xác định:

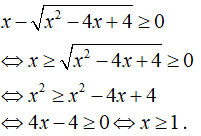
    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Vậy tập xác định là D = [1; +∞].

    b) Ta có: .

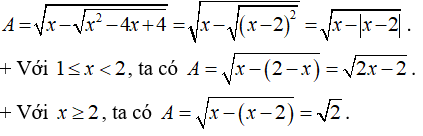
    Bài tập: Căn thức bậc hai và hằng đẳng thức

    Câu 7: Với giá trị nào của a thì mỗi căn thức sau có nghĩa.

    a) a3

    b) -5a

    c) 4-a

    d) 3a+7

    Lời giải:

    a) Để a3 có nghĩa thì a3 ≥ 0 ⇔ a ≥ 0.

    b) Để -5a có nghĩa thì -5a ≥ 0 ⇔ a ≤ 0.

    c) Để 4-a có nghĩa thì 4 – a ≥ 0 ⇔ -a ≥ -4 ⇔ a ≤ 4.

    d) Để 3a+7 có nghĩa thì 3a + 7 ≥ 0 ⇔ 3a ≥ -7 ⇔ a ≥ -73.

    Câu 8: Tính:

    Để học tốt Toán 9 | Giải bài tập Toán 9

    Lời giải:

    Để học tốt Toán 9 | Giải bài tập Toán 9

    Câu 9: Rút gọn biểu thức sau:

    a) 2-32

    b) 3−112

    c) 2a2 với a ≥ 0

    d) 3a−22 với a < 2.

    Lời giải:

    a) 2-32 = |2 - 3| = 2 - 3

    b) 4x23−112 = |3 - 11| = 11 - 3

    c) 2a2 = 2|a| vì a ≥ 0 nên 2|a| = 2a.

    d) 3a−22 = 3|a - 2| vì a < 2 nên 3|a - 2| = 3(2 - a) = 6 - 3a.

    Câu 10: Tìm x biết:

    a) x2 = 7

    b) x2 = |-8|

    c) 4x2 = 6

    d) 9x2 = |-12|

    Lời giải:

    a) x2 = 7 ⇔ |x| = 7

    ⇔ x1 = 7 và x2 = -7

    b) x2 = |-8| ⇔ x2 = 8

    ⇔ |x| = 8 ⇔ x1 = 8 và x2 = -8

    c) 4x2 = 6 ⇔ 2x2 = 6  ⇔ |2x| = 6

    ⇔ 2.|x| = 6  |x|= 3 ⇔ x1 = 3 và x2 = -3

    d) 9x2 = |-12| ⇔ 3x2 = 12

    ⇔ |3x| = 12 ⇔ 3.|x| = 12 |x| = 4

    ⇔ x1 = 4 và x2 = -4.

    III. Bài tập vận dụng

    Câu 1: Với giá trị nào của x thì mỗi biểu thức sau có nghĩa:

    a. \sqrt {2x - 1}

    b. \frac{x}{{{x^2} - 4}} + \sqrt {x - 2}

    g. \sqrt {25 - {x^2}}

    c. \sqrt {9x - 2}

    d. \sqrt {\frac{1}{{3 - 2x}}}

    h. \sqrt {x\left( {x - 1} \right)}

    e. \sqrt {\frac{{ - 2}}{{2x - 1}}}

    f. \sqrt {{x^2} + 4}

    i \sqrt {{x^2} - 5x + 6}

    Câu 2: Thực hiện các phép tính sau:

    a.  \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}}

    b. \sqrt {{{\left( {5 - 2\sqrt 6 } \right)}^2}} - \sqrt {{{\left( {5 + 2\sqrt 6 } \right)}^2}}

    c. \sqrt {{{\left( {\sqrt 2 + 1} \right)}^2}} - \sqrt {{{\left( {\sqrt 2 - 5} \right)}^2}}

    d.  \sqrt {17 - 12\sqrt 2 } + \sqrt {9 + 4\sqrt 2 }

    e. \sqrt {6 - 4\sqrt 2 } + \sqrt {22 - 12\sqrt 2 }

    f. \sqrt {\sqrt 5 - \sqrt {9 - \sqrt {29 - 12\sqrt 5 } } }

    Câu 3: Rút gọn các biểu thức sau đây:

    a. \sqrt {1 - 4x + 4{x^2}} - 2x

    b. {a^2} + \sqrt {{a^4} - 8{a^2} + 16}

    c.  \frac{{\sqrt {{x^2} - 2x + 1} }}{{x - 1}};\left( {x > 1} \right)

    d. 2x - 1 - \frac{{\sqrt {{x^2} - 10x + 25} }}{{x - 5}}

    e. \sqrt {{{\left( {x - 4} \right)}^2}} + \frac{{x - 4}}{{\sqrt {{x^2} - 8x + 16} }}

    f. \sqrt {{x^2} + 2\sqrt {{x^2} - 1} } - \sqrt {{x^2} - 2\sqrt {{x^2} - 1} }

    Câu 4: Giải các phương trình sau:

    a. \sqrt {2x + 5} = \sqrt {1 - x}

    b. \sqrt {x + 2\sqrt {x - 1} } = 2

    c. \sqrt {{x^2} - 4x + 3} = x - 2

    d. \sqrt {{x^2} - 2x + 1} = {x^2} - 1

    Câu 5: Giải các phương trình sau:

    a. \sqrt {1 - 12x + 36{x^2}} = 5

    b. \left| {3x + 1} \right| = \left| {x + 1} \right|

    c. \sqrt {9{x^2} - 12x + 4} - \sqrt {{x^2}} = 0

    d. \sqrt {{x^2} - 1} - {x^2} + 1 = 0

    Câu 6: Thực hiện phép tính

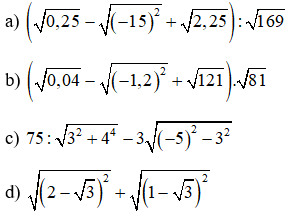
    Dạng toán Liên hệ giữa căn bậc hai và hằng đẳng thức chọn lọc

    e) 8 - 2√7

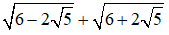
    f) Dạng toán Liên hệ giữa căn bậc hai và hằng đẳng thức chọn lọc

    Câu 7: Rút gọn biểu thức căn bậc 2

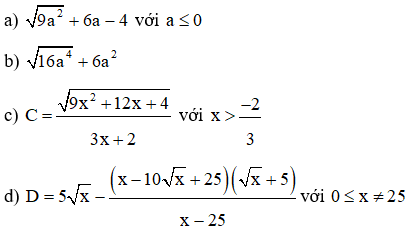
    Dạng toán Liên hệ giữa căn bậc hai và hằng đẳng thức chọn lọc

    Câu 8: Giải phương trình

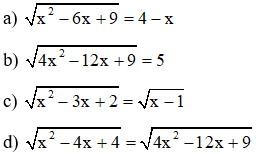
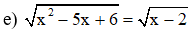
    Dạng toán Liên hệ giữa căn bậc hai và hằng đẳng thức chọn lọc

    Dạng toán Liên hệ giữa căn bậc hai và hằng đẳng thức chọn lọc

    Câu 9: Tính:

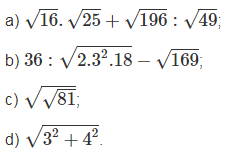
    Câu 10: Tìm x để mỗi căn thức sau có nghĩa:

    Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

    Chuyên đề Liên hệ giữa phép nhân và phép khai phương

    Chuyên đề Liên hệ giữa phép chia và phép khai phương

    Chuyên đề Bảng căn bậc hai

    Chuyên đề Biến đổi đơn giản biểu thức chứa căn bậc hai

    Chuyên đề Rút gọn biểu thức chứa căn thức bậc hai

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 4,001 27/08/2022
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: