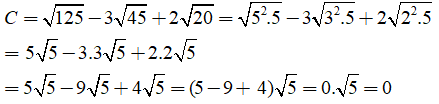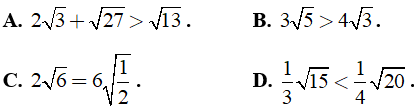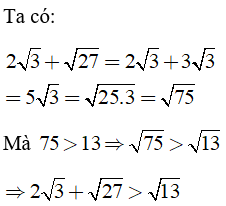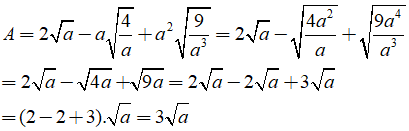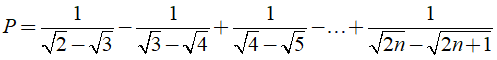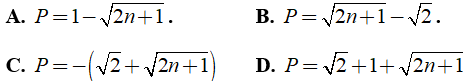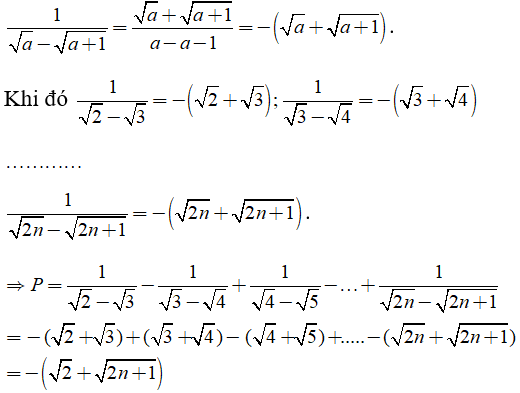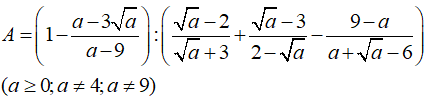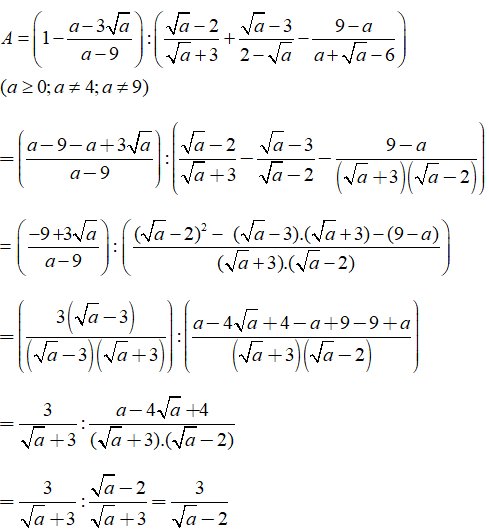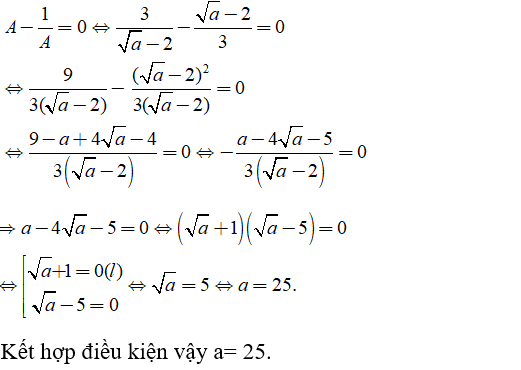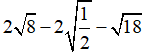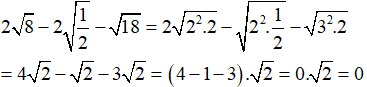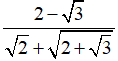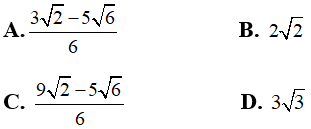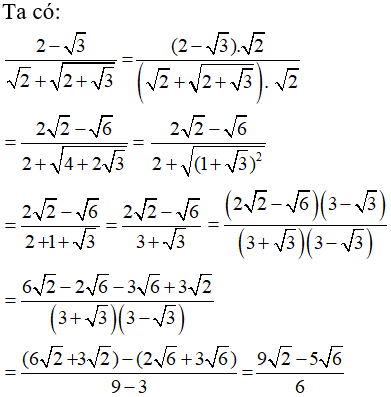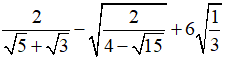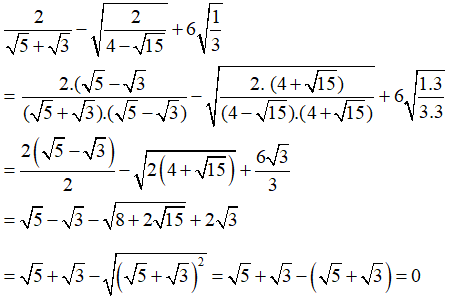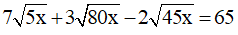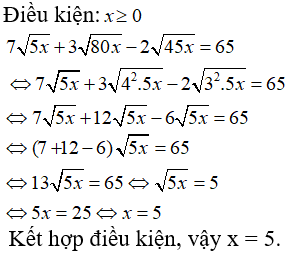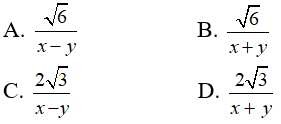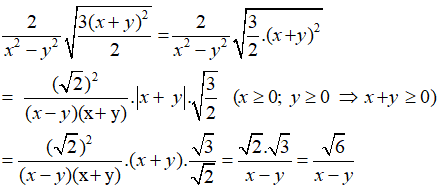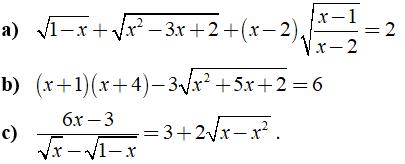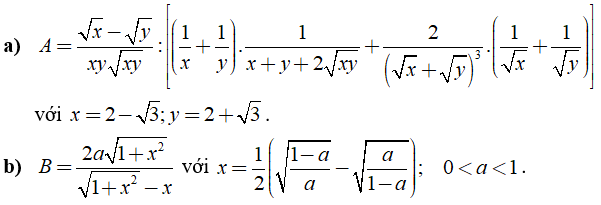Chuyên đề Biến đổi đơn giản biểu thức chứa căn bậc hai (2022) - Toán 9
Với Chuyên đề Biến đổi đơn giản biểu thức chứa căn bậc hai (2022) - Toán 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Biến đổi đơn giản biểu thức chứa căn bậc hai - Toán 9
A. Lý thuyết
1. Đưa một thừa số ra ngoài dấu căn
• Với a ≥ 0, b ≥ 0, ta có: . Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.
• Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.
• Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.
Ví dụ 1.
a) ;
b)
Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có , tức là:
Nếu A ≥ 0 và B ≥ 0 thì ;
Nếu A < 0 và B ≥ 0 thì .
Ví dụ 2. Đưa thừa số ra ngoài căn:
a) với x ≥ 0, y < 0;
b) với x ≥ 0, y ≥ 0.
Lời giải:
a)
(với x ≥ 0, y < 0);
b)
(với x ≥ 0, y ≥ 0).
2. Đưa thừa số vào trong dấu căn
• Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.
Với A ≥ 0 và B ≥ 0 thì .
Với A < 0 và B ≥ 0 thì .
Ví dụ 2. Đưa thừa số vào trong căn:
a) ;
b) với a ≥ 0.
Lời giải:
a)
b)
với a ≥ 0.
• Có thể sử dụng phép đưa thừa số vào trong (hoặc ra ngoài) dấu căn để so sánh các căn bậc hai.
Ví dụ 3. So sánh và .
Lời giải:
Ta có: .
Vì nên .
3. Khử mẫu của biểu thức lấy căn
Tổng quát: Với các biểu thức A, B mà A. B ≥ 0 và B ≠ 0, ta có:
.
Ví dụ 4. Khử mẫu của biểu thức lấy căn
a) ;
b) với a > 0
Lời giải:
a)
b) Vì a > 0 nên 3a > 0. Do đó |3a| = 3a;
Vì a > 0 nên 9a3 > 0. Do đó |9a3| > 9a3.
Khi đó,
4. Trục căn thức ở mẫu
Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số.
Tổng quát:
• Với các biểu thức A, B mà B > 0 ta có:
.
• Với các biểu thức A, B, C mà A ≥ 0, A ≠ B2, ta có:
.
• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:
.
Ví dụ 5. Trục căn thức ở mẫu
a) ;
b) .
Lời giải:
a)
b)
B. Bài tập
I. Bài tập trắc nghiệm
Câu 1: Kết quả của biểu thức rút gọn C = √125 - 3√45 + 2√20 ?
A. √5. B. 0. C. -√5. D. 2√5.
Đưa một thừa số ra ngoài dấu căn
Ta có:
Chọn đáp án B.
Câu 2: Kết quả so sánh nào sau đây đúng ?
Đưa thừa số vào trong dấu căn để sao sánh
Chọn đáp án A.
Câu 3: Rút gọn biểu thức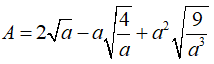 
với a > 0 ?
A. 3a B. a√3 C. 3√a D. a/√3
Lời giải:
Khử mẫu của biểu thức dưới dấu căn
Ta có:
Chọn đáp án C.
Câu 4: Rút gọn biểu thức
Lời giải:
Trục căn thức ở mẫu
Ta có:
Chọn đáp án C.
Câu 5: Cho biểu thức
Tìm giá trị của a để A - 1/A = 0?
A. a = 5 B. a = 3 C. a = 36 D. a = 25
Ta có:
Ta có:
Chọn đáp án D.
Câu 6: Tính 
A. 1
B. 0
C.√2
D.2√2
Chọn đáp án B.
Câu 7: Tính 
Chọn đáp án C.
Câu 8: Tính 
A. 0
B. 1
C. 2
D.3
Chọn đáp án A.
Câu 9: Tìm x biết: 
A. x = 2
B. x = 5
C. x = 10
D. x = 125
Chọn đáp án B.
Câu 10: Rút gọn: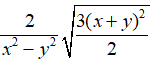 
(với x ≥ 0; y ≥ 0; x ≠ y )
Với x ≥ 0; y ≥ 0; x ≠ y , áp dụng đưa thừa số ra ngoài dấu căn, ta có
Chọn đáp án A.
II. Bài tập tự luận có lời giải
Câu 1: So sánh:
a) và ;
b) và 8.
Lời giải:
a) Ta có:
Vì 50 > 38 nên hay .
Vậy .
b) Ta có:
;
Vì 48 < 64 nên hay .
Vậy .
Câu 2: Rút gọn
a) với x ≥ 0, y ≥ 0 và x ≠ y;
b) với a > 2.
Lời giải:
a) Vì x ≥ 0 và y ≥ 0 nên x + y ≥ 0.
Khi đó, |x + y| = x + y.
Ta có:
b) Ta có:
Vì a > 2 nên a > 0 suy ra |a| = a.
Vì a > 2 nên |a – 2| = a – 2.
Do đó,
Vậy .
Câu 3: Cho biểu thức
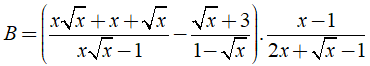(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
Tìm tất cả các giá trị của x để B < 0.
Ta có:
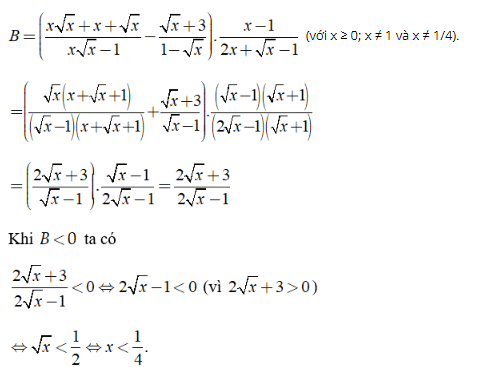
Kết hợp điều kiện ta có x ∈ [0; 1/4].
Câu 4: Giải các phương trình sau:
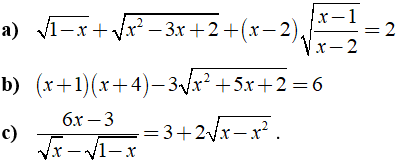
a) Điều kiện xác định:
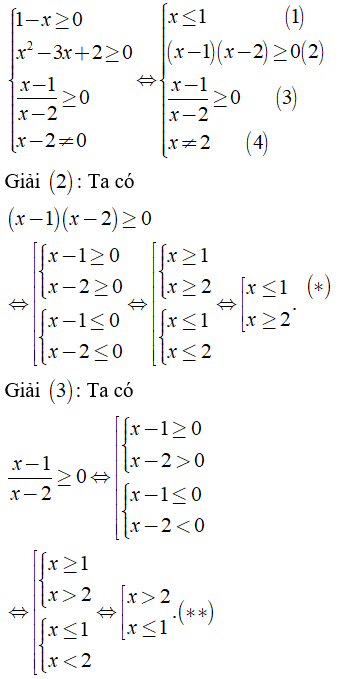
Kết hợp (1), (4), (*) và (**) ta có điều kiện xác định: x ≤ 1
Ta có
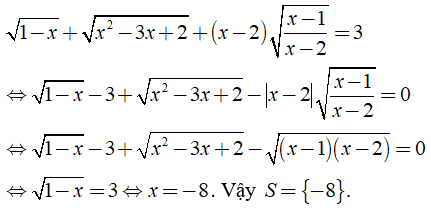
b) Điều kiện xác định: .
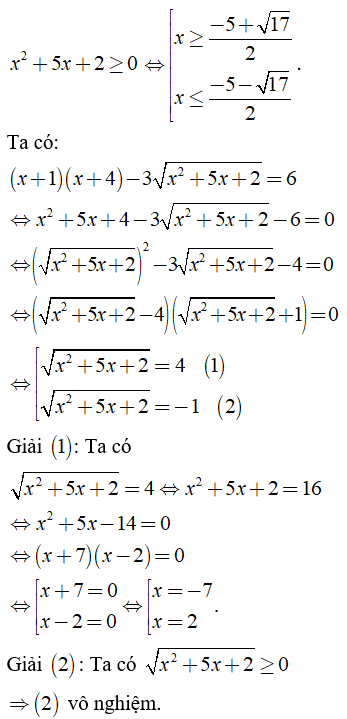
So sánh điều kiện ta có: x = -7; x = 2 (t/m). Vậy S = {-7; 2}.
c) Điều kiện xác định x ∈ [0; 1]\{1/2}.
Ta có:
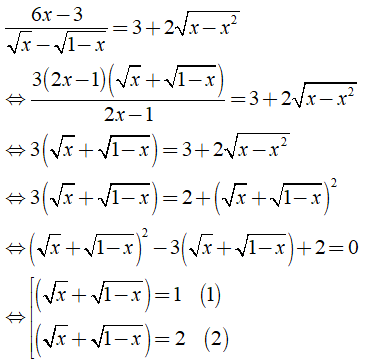
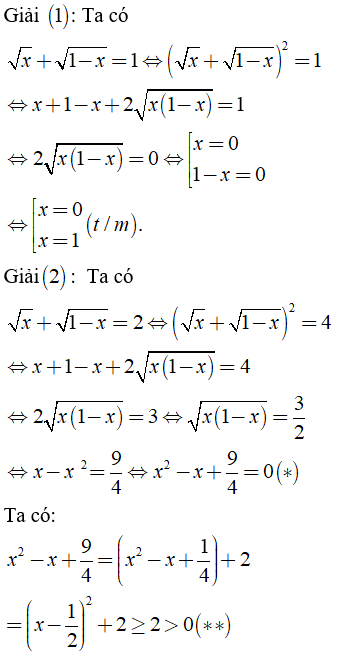
Từ (*) và (**) suy ra phương trình (2) vô nghiệm.
Vậy S = {0; 1}.
Câu 5: Rút gọn các biểu thức sau:
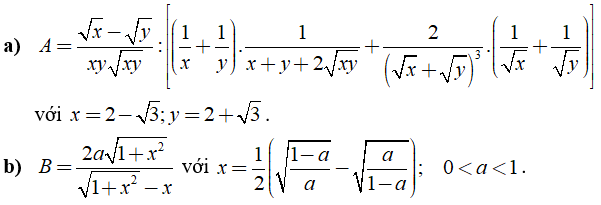
a) Ta có:
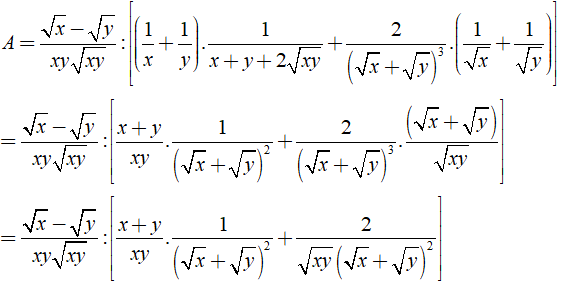
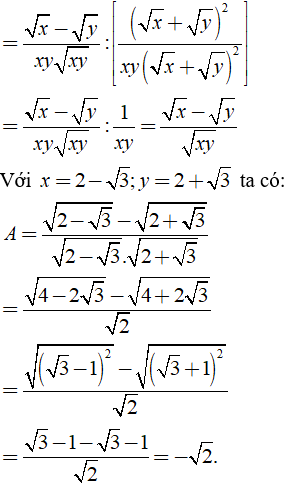
b) Ta có
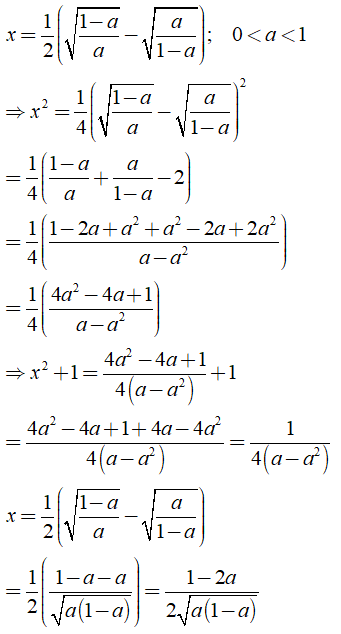
Khi đó: .
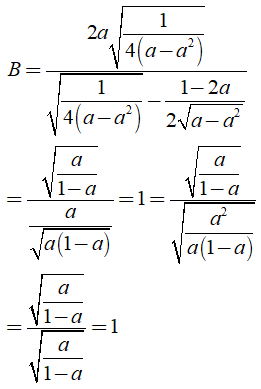
Câu 6: Chứng minh rằng
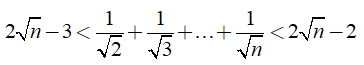(n ∈ N; n ≥ 2)
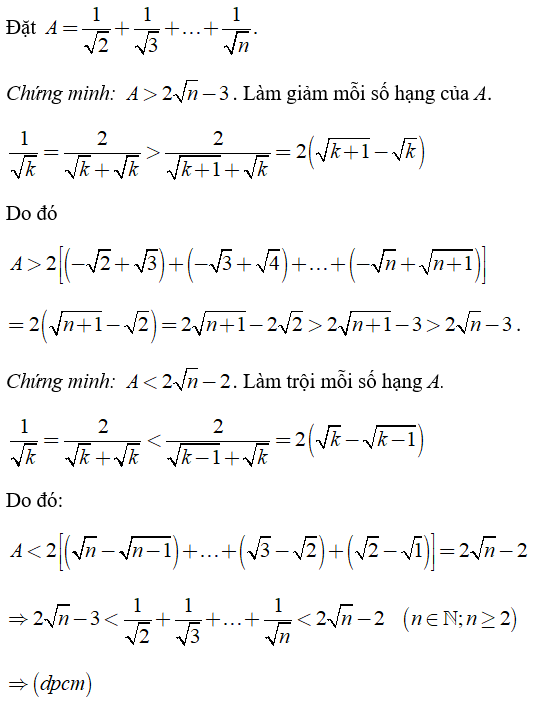
Câu 7: Rút gọn biểu thức
a) ;
b) .
Lời giải
a)
=
b)
= .
Câu 8: Đưa thừa số ra ngoài dấu căn
a) với b ≥ 0;
b) với a < 0.
Lời giải
a) (do b ≥ 0)
b) (do a < 0)
Câu 9: Với a ≥ 0, b ≥ 0, chứng tỏ .
Lời giải
(do a ≥ 0;b ≥ 0)
Câu 10: Rút gọn biểu thức
a) ;
b) .
Lời giải
a)
=
b)
= .
III. Bài tập vận dụng
Câu 1: Cho biểu thức
(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
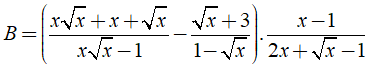
Tìm tất cả các giá trị của x để B < 0.
Câu 2: Giải các phương trình sau:
Câu 3: Rút gọn các biểu thức sau:
Câu 4: Rút gọn biểu thức
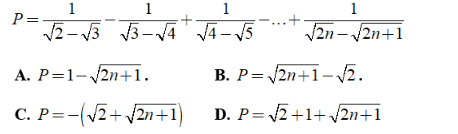
Câu 5: Cho biểu thức
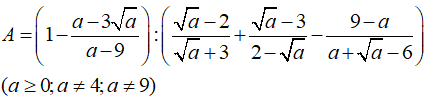
Tìm giá trị của a để A - 1/A = 0?
A. a = 5 B. a = 3 C. a = 36 D. a = 25
Câu 6: Cho biểu thức
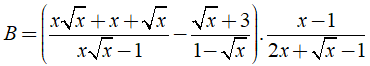(với x ≥ 0; x ≠ 1 và x ≠ 1/4).
Tìm tất cả các giá trị của x để B < 0.
Câu 7: Giải các phương trình sau:
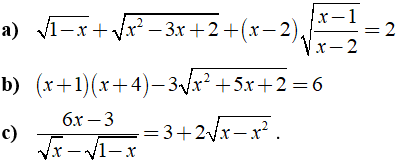
Câu 8: Rút gọn các biểu thức sau:
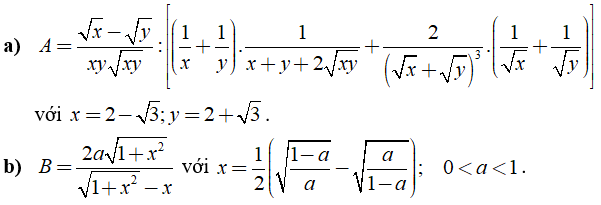
Câu 9: Chứng minh rằng
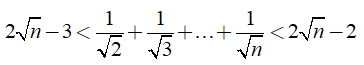(n ∈ N; n ≥ 2)
Câu 10: Viết các số hoặc biểu thức dưới dấu căn thành dạng tích rồi đưa thừa số ra ngoài dấu căn.
Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:
Chuyên đề Rút gọn biểu thức chứa căn thức bậc hai
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9