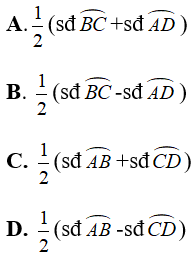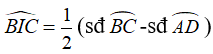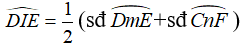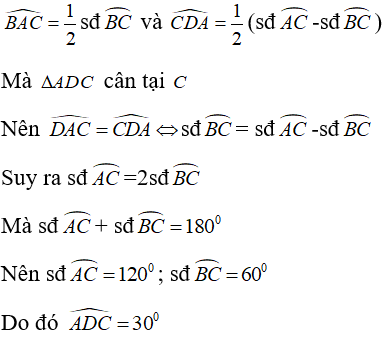Chuyên đề Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn (2022) - Toán 9

Chuyên đề Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn - Toán 9

A. Lý thuyết

1. Góc có đỉnh ở bên trong đường tròn

- Góc có đỉnh nằm bên trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.

- Định lí: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Ví dụ 1. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (điểm E nằm bên trong đường tròn) như hình vẽ.

Trong hình vẽ trên, $\widehat{BEC}$ là góc có đỉnh nằm ở bên trong đường tròn chắn hai cung là .

Do đó,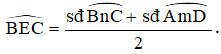 

2. Góc có đỉnh nằm bên ngoài đường tròn

- Góc có đỉnh ở bên ngoài đường tròn là góc có đỉnh nằm ngoài đường tròn và các cạnh đều có điểm chung với đường tròn.

- Định lí: Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Ví dụ 2. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (điểm E nằm bên ngoài đường tròn) như hình vẽ.

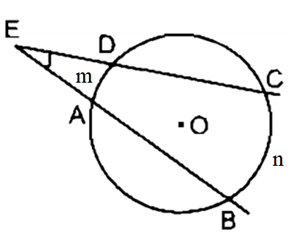
Trong hình vẽ trên, $\widehat{BEC}$ là góc có đỉnh nằm ở bên ngoài đường tròn chắn hai cung là $\stackrel{⏜}{BnC},\stackrel{⏜}{AmD}$.

Do đó,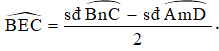 

B. Bài tập

I. Bài tập trắc nghiệm

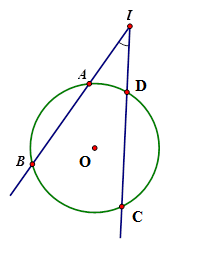
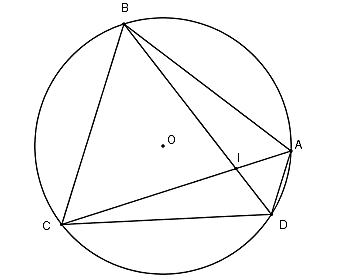
Câu 1: Cho hình vẽ dưới đây , góc BIC có số đo bằng

Lời giải:

Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Chọn đáp án B

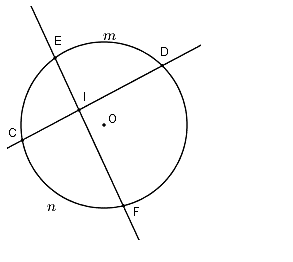
Câu 2: Cho hình vẽ dưới đây , góc DIE có số đo bằng

Lời giải:

Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn

Chọn đáp án A

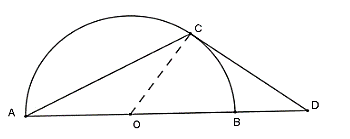
Câu 3: Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung nhỏ AB (cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC

A. 40°

B. 45°

C. 60°

D. 30°

Lời giải:

Xét nửa (O) có

Chọn đáp án D

Câu 4: Trên (O) lấy bốn điểm A, B, C, D theo thứ tự sao cho cung AB = cung BC = cung CD . Gọi I là giao điểm của BD và AC , biết 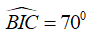 . Tính 

A. 20°

B. 15°

C. 35°

D. 30°

Lời giải:

Chọn đáp án B

Câu 5: Cho đường tròn (O) và dây AB; AC cách đều tâm. Trên cung nhỏ AC lấy điểm M. Gọi S là giao điểm của AM và BC. Góc nào bằng góc 

Lời giải:

Chọn đáp án C.

Câu 6: Cho đường trò (O) và 2 dây AB, CD cắt nhau tại điểm E. Tìm hệ thức đúng?

Lời giải:

Chọn đáp án D.

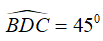
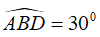
Câu 7: Cho đường tròn (O), tam giác BCD nội tiếp đường tròn với . Lấy điểm A trên cung BD – không chứa điểm C sao cho AB và CD cắt nhau tại điểm S nằm ngoài đường tròn (O) và .Tính 

A. 15°

B.20°

C. 45°

D. 30°

Lời giải:

Chọn đáp án A.

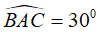
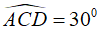
Câu 8: Cho đường tròn (O) và tam ABC nội tiếp đường tròn sao cho . Trên cung AC –không chứa điểm B lấy điểm D sao cho , AC cắt BD tại M nằm trong đường tròn. Tính số đo góc 

A. 120°

B. 60°

C. 150°

D.165°

Lời giải:

Chọn đáp án A.

Câu 9: Cho đường tròn (O) ngoại tiếp tam giác ABC, đường thẳng BO cắt đường tròn tại D. Gọi H là giao điểm của AC và BD. Tính 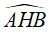, biết rằng 

A. 600

B. 1200

C. 1050

D.900

Lời giải:

Chọn đáp án D.

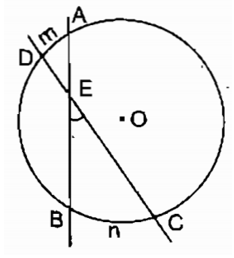
Câu 10: Cho đường tròn (O) và 4 điểm A,B, C, D cùng nằm trên đường tròn sao cho AC và BD cắt nhau tại điểm M nằm trong đường tròn, AB và CD cắt nhau tại điểm S nằm ngoài đường tròn. So sánh hai góc 

Lời giải:

Chọn đáp án C.

II. Bài tập tự luận có lời giải

Câu 1: Từ điểm M nằm ngoài đường thẳng (O) vẽ tiếp tuyến MC với C là tiếp điểm và cát tuyến MAB (A nằm giữa M và B) và A; B; C thuộc (O). Gọi D là điểm chính giữa cung AB không chứa C, CD cắt AB tại I. Chứng minh:

a) $\widehat{MCD}=\widehat{BID}$

b) $MI=MC$.

Lời giải:

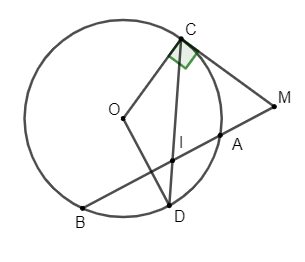
a) Ta có:

$\widehat{MCD}$ là góc tạo bởi tia tiếp tuyến và dây cung chắn cung $\stackrel{⏜}{CD}$

$\Rightarrow \widehat{MCD}=\frac{1}{2}$ sđ $\stackrel{⏜}{CD}$  (định lí)    (1)

$\widehat{BID}$ là góc có đỉnh nằm trong đường tròn chắn cung $\stackrel{⏜}{CA}$ và $\stackrel{⏜}{BD}$

$\Rightarrow \widehat{BID}=\frac{1}{2}$ (sđ $\stackrel{⏜}{CA}$ + sđ $\stackrel{⏜}{BD}$) (định lí)  (2)

Ta có:

$\stackrel{⏜}{CD}=\stackrel{⏜}{CA}+\stackrel{⏜}{AD}$

Mà $\stackrel{⏜}{AD}=\stackrel{⏜}{BD}$ (do D là điểm chính giữa cung $\stackrel{⏜}{AB}$)

Do đó $\stackrel{⏜}{CD}=\stackrel{⏜}{CA}+\stackrel{⏜}{BD}$ (3)

Từ (1); (2); (3) $\Rightarrow \widehat{MCD}=\widehat{BID}$ (điều phải chứng minh)

b) Ta có:

$\widehat{CIM}$ và $\widehat{BID}$ là hai góc đối đỉnh

$\Rightarrow \widehat{CIM}=\widehat{BID}$(tính chất)

Mà $\widehat{MCD}=\widehat{BID}$(chứng minh ở câu a)

Do đó $\widehat{CIM}=\widehat{MCD}$

Xét tam giác CMI có

$\widehat{CIM}=\widehat{MCI}$

$\Rightarrow \Delta CMI$ cân tại M (dấu hiệu nhận biết)

=> MI = MC (tính chất).

Câu 2: Cho tam giác ABC ngoại tiếp đường tròn (I). Các tia AI; BI; CI cắt đường tròn ngoại tiếp tam giác ABC tại D, E, F. Dây EF cắt AB, AC lần lượt tại M và N. Chứng minh:

a) DI = BD.

b) AM = AN.

Lời giải:

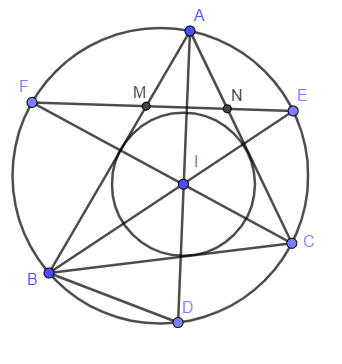
a) Vì I là tam đường tròn nội tiếp tam giác ABC nên AI là phân giác $\widehat{A}$.

Mà AI cắt đường tròn ngoại tiếp tam giác ABC tại D nên D là điểm chính giữa cung $\stackrel{⏜}{BC}$.

=> sđ $\stackrel{⏜}{BD}$ = sđ $\stackrel{⏜}{CD}$ (1).

Vì I là tâm đường tròn nội tiếp tam giác ABC nên BI là đường phân giác $\widehat{B}$.

Mà BI cắt đường tròn ngọa tiếp tam giác ABC tại E nên E là điểm chính giữa cung $\stackrel{⏜}{AC}$.

=> sđ $\stackrel{⏜}{AE}$= sđ $\stackrel{⏜}{EC}$(2).

Ta có:

$\widehat{BID}$ là góc có đỉnh nằm trong đường tròn ngoại tiếp tam giác ABC

$\Rightarrow \widehat{BID}=\frac{1}{2}$(sđ $\stackrel{⏜}{AE}$+ sđ $\stackrel{⏜}{BD}$)  (3)

$\widehat{IBD}$ là góc nội tiếp của đường tròn ngoại tiếp tam giác ABC chắn cung $\stackrel{⏜}{DE}$.

$\Rightarrow \widehat{BID}=\frac{1}{2}$sđ $\stackrel{⏜}{DE}$

Mà $\stackrel{⏜}{DE}=\stackrel{⏜}{EC}+\stackrel{⏜}{CD}$ nên $\widehat{IBD}=\frac{1}{2}$(sđ $\stackrel{⏜}{EC}$+ sđ $\stackrel{⏜}{CD}$) (4)

Từ (1) (2) (3) (4) $\Rightarrow \widehat{BID}=\widehat{IBD}$

Xét tam giác IDB có:

$\widehat{BID}=\widehat{IBD}$

$\Rightarrow \Delta IDB$ cân tại D

$\Rightarrow DI=DB$ (tính chất)

b) Vì I là tam đường tròn nội tiếp tam giác ABC nên CI là phân giác $\widehat{C}$.

Mà CI cắt đường tròn ngoại tiếp tam giác ABC tại F nên F là điểm chính giữa cung $\stackrel{⏜}{AB}$.

=> sđ $\stackrel{⏜}{BF}$ = sđ $\stackrel{⏜}{A\text{}F}$ (5).

Ta có:

$\widehat{AN\text{}F}$ là góc có đỉnh nằm bên trong đường tròn

$\Rightarrow \widehat{AN\text{}F}=\frac{1}{2}$(sđ $\stackrel{⏜}{A\text{}F}$+ sđ $\stackrel{⏜}{EC}$)  (6)

$\widehat{AME}$ là góc có đỉnh nằm bên trong đường tròn

$\Rightarrow \widehat{AME}=\frac{1}{2}$(sđ $\stackrel{⏜}{AE}$ + sđ $\stackrel{⏜}{FB}$) (7)

Từ (1); (5); (6); (7) $\Rightarrow \widehat{AN\text{}F}=\widehat{AME}$

Xét tam giác AMN có:

$\widehat{AN\text{}M}=\widehat{AMN}$

$\Rightarrow \Delta AMN$ cân tại A

$\Rightarrow AM=AN$(tính chất).

Câu 3: Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:

a) Tam giác BDI là tam giác cân;

b) DE là đường trung trực của IC.

Lời giải:

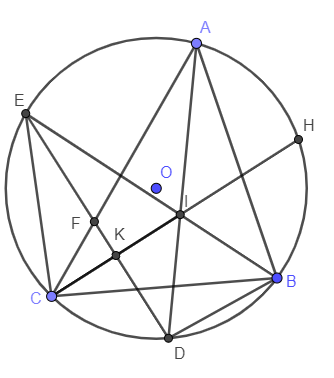
a) ) Vì  AI là phân giác $\widehat{A}$ của tam giác ABC và AI cắt đường tròn ngoại tiếp tam giác ABC tại D nên D là điểm chính giữa cung $\stackrel{⏜}{BC}$.

=> sđ $\stackrel{⏜}{BD}$ = sđ $\stackrel{⏜}{CD}$ $=\frac{1}{2}$sđ $\stackrel{⏜}{BC}$ (1).

Vì  BI là phân giác $\widehat{B}$ của tam giác ABC và BI cắt đường tròn ngoại tiếp tam giác ABC tại E nên E là điểm chính giữa cung $\stackrel{⏜}{AC}$.

=>sđ $\stackrel{⏜}{AE}$ = sđ $\stackrel{⏜}{CE}$ $=\frac{1}{2}$sđ $\stackrel{⏜}{AC}$ (2).

Ta có:

$\widehat{BID}$ là góc có đỉnh nằm trong đường tròn ngoại tiếp tam giác ABC

$\Rightarrow \widehat{BID}=\frac{1}{2}$ (sđ $\stackrel{⏜}{AE}$+ sđ $\stackrel{⏜}{BD}$)  (3)

$\widehat{IBD}$ là góc nội tiếp của đường tròn ngoại tiếp tam giác ABC chắn cung $\stackrel{⏜}{DE}$.

$\Rightarrow \widehat{IBD}=\frac{1}{2}$sđ $\stackrel{⏜}{DE}$

Mà $\stackrel{⏜}{DE}=\stackrel{⏜}{EC}+\stackrel{⏜}{CD}$ nên $\widehat{IBD}=\frac{1}{2}$(sđ $\stackrel{⏜}{EC}$+ sđ $\stackrel{⏜}{CD}$) (4)

Từ (1) (2) (3) (4) $\Rightarrow \widehat{BID}=\widehat{IBD}$

Xét tam giác IDB có:

$\widehat{BID}=\widehat{IBD}$

$\Rightarrow \Delta IDB$ cân tại D

b) Gọi giao điểm của DE và IC là K, CI cắt đường tròn tại điểm thứ hai là H.

Vì  CI là phân giác $\widehat{C}$ của tam giác ABC và CI cắt đường tròn ngoại tiếp tam giác ABC tại H nên H là điểm chính giữa cung $\stackrel{⏜}{AB}$.

=> sđ $\stackrel{⏜}{AH}$ = sđ $\stackrel{⏜}{BH}$= $\frac{1}{2}$sđ $\stackrel{⏜}{AB}$ (5).

Ta có:

$\widehat{EKC}$ là góc có đỉnh nằm trong đường tròn

$\Rightarrow \widehat{EKC}$= $\frac{1}{2}$(sđ $\stackrel{⏜}{EC}$+ sđ $\stackrel{⏜}{DH}$)

Mà $\stackrel{⏜}{DH}=\stackrel{⏜}{BD}+\stackrel{⏜}{BH}$

$\Rightarrow \widehat{EKC}=\frac{1}{2}$(sđ $\stackrel{⏜}{EC}$+ sđ $\stackrel{⏜}{BD}$+ sđ $\stackrel{⏜}{BH}$)

Theo (1); (2); (5) $\Rightarrow \widehat{EKC}=\frac{1}{4}$(sđ $\stackrel{⏜}{AC}$+ sđ $\stackrel{⏜}{BC}$+ sđ $\stackrel{⏜}{AB}$)

$\iff \widehat{EKC}=90°$

$\Rightarrow DE\perp IC$

Lại có: $\widehat{CED}$ là góc góc nội tiếp chắn cung $\stackrel{⏜}{CD}$

$\widehat{BED}$ là góc nội tiếp chắn chung $\stackrel{⏜}{BD}$

Mà $\stackrel{⏜}{BD}=\stackrel{⏜}{CD}$

Do đó: $\widehat{CED}=\widehat{BED}$

Xét tam giác CEK và tam giác IEK có:

$\widehat{CEK}=\widehat{IEK}$ (do $\widehat{CED}=\widehat{BED}$)

EK chung

$\widehat{EKC}=\widehat{EKI}=90°$

Do đó: $\Delta CEK=\Delta IEK$ (c – g – c)

$\Rightarrow IK=KC$(hai cạnh tương ứng)

Ta có:

$\left\{\begin{array}{l}IK=KC\\ DE\perp IC\end{array}\right.\Rightarrow$DE là đường trung trực của IC.

Câu 4: Cho tam giác ABC phân giác AD. Vẽ đường tròn (O) đi qua A, D và tiếp xúc với BC tại D. Đường tròn này cắt AB, AC lần lượt tại E, F. Chứng minh: EF // BC.

Lời giải:

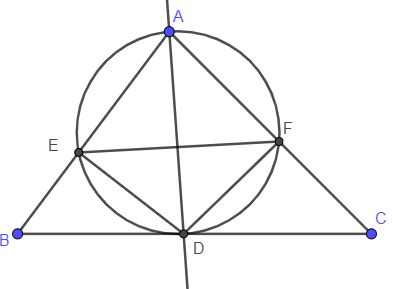
Ta có: $\widehat{BDE}$ là góc tạo bởi tiếp tuyến và dây cung và $\widehat{BDE}$ chắn cung $\stackrel{⏜}{DE}$

Lại có: $\widehat{EAD}$ là góc nội tiếp chắn cung $\stackrel{⏜}{DE}$

$\Rightarrow \widehat{BDE}=\widehat{EAD}$ (hệ quả)

Xét tam giác BED và tam giác BDA có:

$\widehat{BDE}=\widehat{EAD}$ (chứng minh trên)

$\widehat{B}$ chung

Do đó: $\Delta BED\backsim \Delta BDA$(g – g)

$\Rightarrow \widehat{BED}=\widehat{DEA}$ (hai góc tương ứng)

Mà $\widehat{BED}+\widehat{DEA}=180°$

Do đó $\Rightarrow \widehat{BED}=\widehat{DEA}=90°$

Lại có:

Xét tam giác BED vuông tại E ta có:

$\widehat{EBD}+\widehat{EDB}=90°$

$\Rightarrow \widehat{EBD}=90°-\widehat{EDB}$ (1)

Lại có: $\widehat{DEF}+\widehat{FEA}=90°$

$\Rightarrow \widehat{FEA}=90°-\widehat{DE\text{}F}$ (2)

Lại có AD là tia phân giác $\widehat{A}$$\Rightarrow \stackrel{⏜}{ED}=\stackrel{⏜}{FD}$

Mà $\widehat{EDB}$ là góc tạo vởi tia tiếp tuyến và dây cung chắn cung $\stackrel{⏜}{ED}$

Và $\widehat{DE\text{}F}$ là góc nội tiếp chắn cung $\stackrel{⏜}{FD}$

Do đó $\widehat{DE\text{}F}=\widehat{EDB}$ (3)

Từ (1); (2); (3) $\Rightarrow \widehat{EBD}=\widehat{FEA}$

Mà hai góc này ở vị trí đồng vị

=> EF // BC

Câu 5: Cho đường tròn đường tròn (O) có hai dây AB và CD cắt nhau tại M như hình vẽ. Tính số đo của cung BD, biết $\widehat{AMB}={120}^o$.

Lời giải:

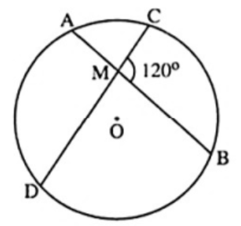
Câu 6: Cho đường tròn đường tròn (O) đường kính BC. Lấy điểm A nằm trên đường tròn, vẽ tiếp tuyến AM (A là tiếp điểm). Tính $\widehat{AMC}$, biết số đo cung AC là 120^o.

Lời giải:

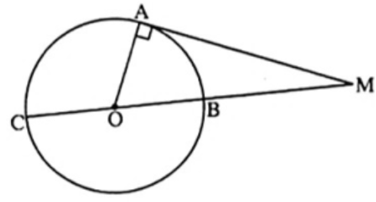
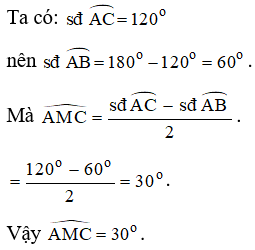
Câu 7: Từ điểm A nằm bên ngoài đường tròn (O) kẻ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM vuông góc với tia phân giác góc BAC tại H cắt CD tại E. Chứng minh BM là đường phân giác góc CBD.

Lời giải:

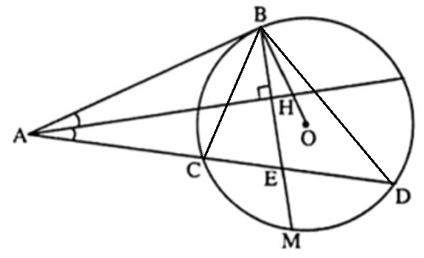
∆ABE có AH là đường phân giác đồng thời là đường cao nên ∆ABE cân tại đỉnh A.

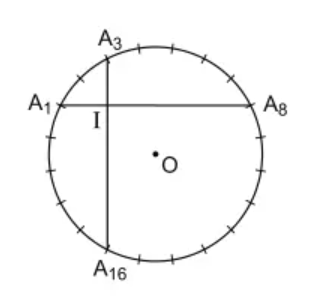
Đường tròn (O) được chia thành 20 cung bằng nhau nên số đo mỗi cung bằng: ${360}^o:20={18}^o$

Gọi giao điểm của $A_1{A}_8$  và $A_3{A}_{16}$  là I

Ta có: sđ$\stackrel{⏜}{A_1{A}_3}={2.18}^o={36}^o$  ; sđ$\stackrel{⏜}{A_8{A}_{16}}={8.18}^o={144}^o$

Ta có: ${\widehat{A_{1}IA}}_3=\frac{1}{2}\left(\text{sd}{\stackrel{⏜}{A_{1}A}}_3+sd\stackrel{⏜}{A_8{A}_{16}}\right)$  (góc có đỉnh ở trong đường tròn (O))

$\Rightarrow \widehat{A_{1}I{A}_3}=\frac{1}{2}\left({36}^o+{144}^o\right)={90}^o$

Do đó, $A_1{A}_8$  vuông góc với dây $A_3{A}_{16}$  tại I.

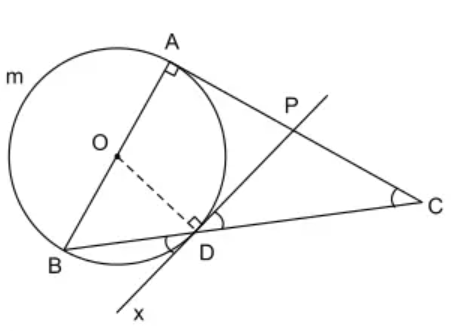
Kẻ tia đối của tia CP là Cx.

Xét đường tròn (O) có $\widehat{C}$  là góc có đỉnh ở ngoài đường tròn chắn cung AmB và cung nhỏ AD.

$\Rightarrow \widehat{C}=\frac{1}{2}\left(sđ\stackrel{⏜}{AmB}-sđ\stackrel{⏜}{AD}\right)$

Mà sđ$\stackrel{⏜}{AmB}$  = sđ$\stackrel{⏜}{ADB}={180}^o$

 $\Rightarrow \widehat{C}=\frac{1}{2}\left(sđ\stackrel{⏜}{ADB}-sđ\stackrel{⏜}{AD}\right)=\frac{1}{2}sđ\stackrel{⏜}{\text{D}B}$ (1)

Mặt khác, ta có:  $\widehat{CDP}=\widehat{BDx}$(hai góc đối đỉnh) (2)

$\widehat{BDx}=\frac{1}{2}$sđ$\stackrel{⏜}{BD}$  (góc giữa tia tiếp tuyến và dây cung) (3)

Từ (1), (2) và (3) ta suy ra: $\widehat{C}=\widehat{CDP}$

Do đó, tam giác PCD cân tại P

⇒ PD = PC.

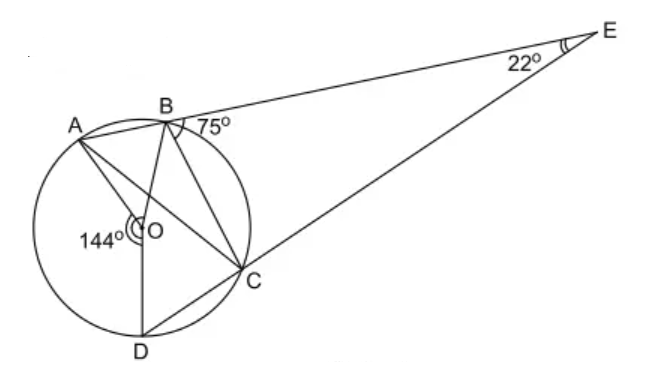
Xét đường tròn (O) ta có:

Góc E là góc có đỉnh ở ngoài đường tròn chắn cung nhỏ BC và cung nhỏ AD

$\Rightarrow \widehat{E}=\frac{1}{2}\left(sđ\stackrel{⏜}{AD}-sđ\stackrel{⏜}{BC}\right)$

 

Lại có: sđ$\stackrel{⏜}{AD}=\widehat{AOD}={144}^o$  (góc ở tâm chắn cung)

$\Rightarrow {22}^o=\frac{1}{2}\left({144}^o-sđ\stackrel{⏜}{BC}\right)\Rightarrow sđ\stackrel{⏜}{BC}={100}^o$

 

Ta có:  $\widehat{BAC}=\frac{1}{2}sđ\stackrel{⏜}{BC}$(góc nội tiếp chắn cung)

$\Rightarrow \widehat{BAC}=\frac{1}{2}{.100}^o={50}^o$

 

Xét tam giác ABC có:

Góc CBE là góc ngoài tại đỉnh B

 $\Rightarrow \widehat{CBE}=\widehat{BAC}+\widehat{ACB}$ (tính chất góc ngoài của tam giác)

$\Rightarrow \widehat{ACB}=\widehat{CBE}-\widehat{BAC}={75}^o-{50}^o={25}^o$

Mặt khác, ta có:  $\widehat{ACB}=\frac{1}{2}\widehat{AOB}$(hệ quả của góc nội tiếp)

$\Rightarrow \widehat{AOB}=2.\widehat{ACB}={2.25}^o={50}^o$

$\Rightarrow \widehat{AOB}=\widehat{BAC}={50}^o$.

III. Bài tập vận dụng

Câu 1: Từ điểm P nằm ngoài đường tròn (O), vẽ tiếp tuyến PA với đường tròn và cát tuyến PBC với P, B, C thuộc (O).

a) Biết PC = 25cm, PB = 49 cm. Đường kính của đường tròn (O) là 50cm. Tính PO.

b) Đường phân giác của góc $\widehat{BAC}$ cắt PB ở I và cắt (O) tại D. Chứng minh DB là tiếp tuyến của đường tròn ngoại tiếp tam giác AIB.

Câu 2: Cho đường tròn (O) và một điểm P nằm ngoài đường tròn (O). Kẻ cát tuyến PAB và tiếp tuyến PT với A, B, T thuộc (O). Đường phân giác của góc $\widehat{ATB}$ cắt AB tại D. Chứng minh PT = PD.

Câu 3: Cho tam giác ABC nội tiếp đường tròn (O). Các tia phân giác góc B và góc C cắt nhau tại I và cắt (O) tại D và E. Dây DE cắt cạnh AB và AC tại M và N. Chứng minh:

a) Các tam giác AMN, EAI và DAI là những tam giác cân.

b) Tứ giác AMIN là hình thoi.

Câu 4: Cho điểm P nằm ngoài đường tròn (O), kẻ hai cát tuyến PAB và PCD (A nằm giữa P và B và C nằm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q.

a) Cho biết $\widehat{P}=60°$ và $\widehat{AQC}=80°$. Tính $\widehat{BCD}$.

b) Chứng minh PC.PD = PA.PB

Câu 5: Từ một điểm A nằm bên ngoài đường tròn (O), vẽ tiếp tuyến AB và cát tuyến ACD. Tia phân giác của góc $\widehat{BAC}$ cắt BC và BD lần lượt tại M và N. Vẽ dây BF vuông góc với MN, cắt MN tại H, cắt CD tại E. Chứng minh:

a) Tam giác BMN cân.

b) $F{D}^2=FE.FB$.

Câu 6: Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE = $\sqrt{2}R$. Vẽ dây CF đi qua E. Tiếp tuyến của đường tròn F cắt CD tại M, vẽ dây AF cắt CD tại N. Chứng minh:

a) Tia CF là tia phân giác của góc $\widehat{BCD}$;

b) MF // AC;

c) MN; OD; OM có độ dài là ba cạnh của tam giác vuông.

Câu 7: Cho tam giác MNP nội tiếp đường tròn (O). Điểm D di chuyển trên cung MP. Gọi E là giao điểm của MP và ND, Gọi F là giao điểm của MG và NP. Chứng minh: $\widehat{MFN}=\widehat{MND}$.

Câu 8: Tam giác MNP nội tiếp đường tròn (O), các điểm I, K, H là điểm chính giữa các cung MN, NP, PM. Gọi J là giao điểm của IK và MN, G là giao điểm của HK và MP. Chứng minh JG song song với NP.

Câu 9: Từ điểm M nằm ngoài đường tròn (O), vẽ tiếp tuyến MA và cát tuyến MCB với A, B, C thuộc (O). Phân giác góc $\widehat{BAC}$ cắt BC tại D, cắt (O) tại N. Chứng minh:

a) MA = MD;

b) Cho cát tuyến MBC quay quanh M và luôn cắt đường tròn. Chứng minh MB.MC không đổi;

c) $N{B}^2=NA.ND$.

Câu 10: Trên đường tròn (O) lấy ba điểm A, B, C. Gọi M, N, P theo thứ tự là điểm chính giữa các cung AB; BC; AC. BP cắt AN tại I, NM cắt AB tại E. Gọi D là giao điểm của AN và BC.

Chứng minh:

a) Tam giác BNI cân;

b) AE.BN = EB.AN;

c) EI // BC;

d) $\frac{AN}{BN}=\frac{AB}{BD}$.

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Cung chứa góc

Chuyên đề Tứ giác nội tiếp

Chuyên đề Đường tròn ngoại tiếp. Đường tròn nội tiếp

Chuyên đề Độ dài đường tròn, cung tròn

Chuyên đề Diện tích hình tròn, hình quạt tròn