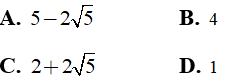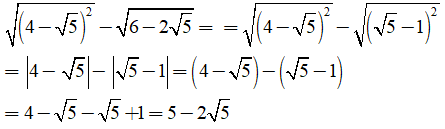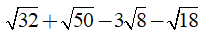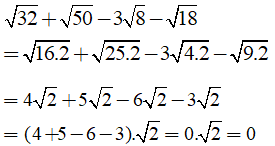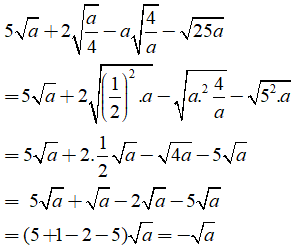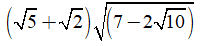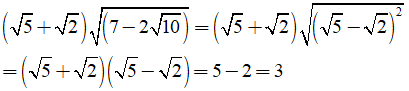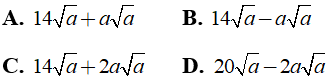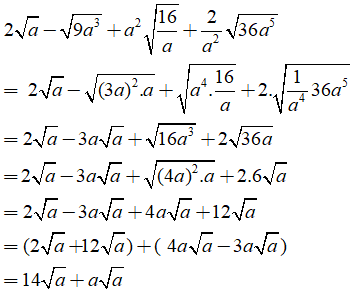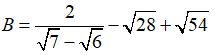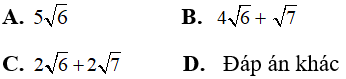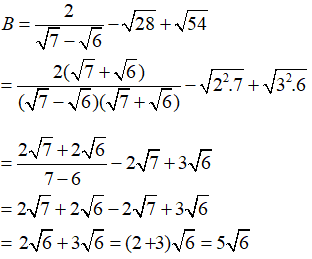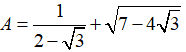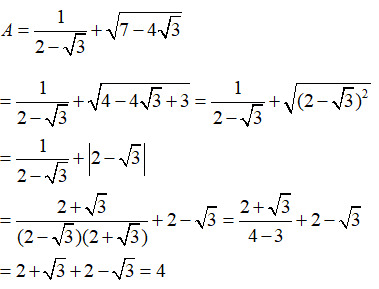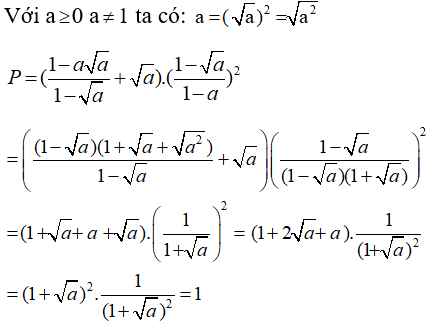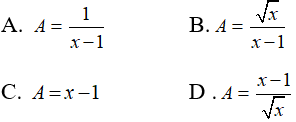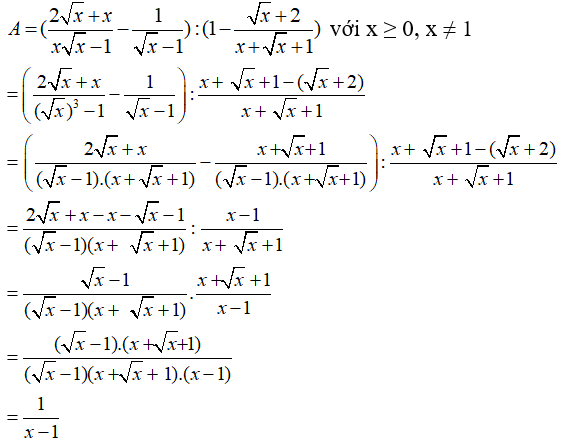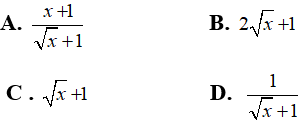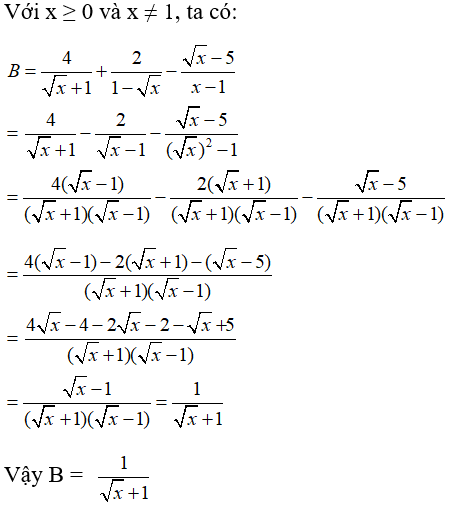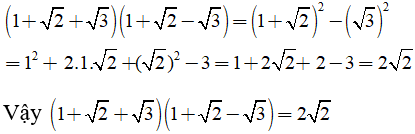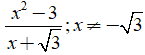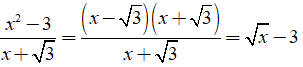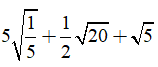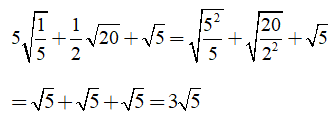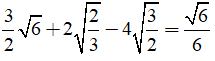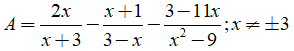Chuyên đề Rút gọn biểu thức chứa căn thức bậc hai (2022) - Toán 9

Với Chuyên đề Rút gọn biểu thức chứa căn thức bậc hai (2022) - Toán 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.

1 2,991 27/08/2022
Tải về
Trang trước
Trang sau  

Chuyên đề Rút gọn biểu thức chứa căn thức bậc hai - Toán 9

A. Lý thuyết

- Để rút gọn biểu thức chứa căn bậc hai, ta cần vận dụng phối hợp các phép tính và các phép biến đổi đã biết.

- Khi rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thứa và khai phương thì thứ tự thực hiện: khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ.

Ví dụ. Rút gọn 4√a+12√a9−a√4a+√3 với a > 0.

Lời giải:

Vì a > 0 nên |a| = a.

Ta có, 4√a+12√a9−a√4a+√3

=4√a+12√a√9−a√4aa2+√3

=4√a+12√a3−a2√a|a|+√3

=4√a+4√a−a2√aa+√3

=8√a−2√a+√3

=6√a+√3

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Giá trị của biểu thức 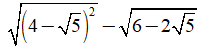Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án là?

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Lời giải:

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án C.

Câu 2: Giá trị của biểu thức Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

A. 1

B. 0

C. 2

D. 3

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án B.

Câu 3: Rút gọn biểu thức 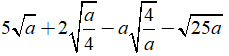Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án với a > 0 ta được

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án D.

Câu 4: Giá trị của biểu thức Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

A. 4

B. 5

C. 2

D. 3

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án D.

Câu 5: Rút gọn biểu thức 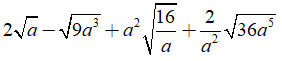Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án với a > 0 ta được

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án A.

Câu 6: Rút gọn biểu thức : Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

 

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án A.

Câu 7: Rút gọn biểu thức Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

A. 1

B. 2

C. 3

D. 4

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án D.

Câu 8: Rút gọn biểu thức: 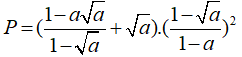Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án (với a ≥ 0;a ≠ 1)

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án C.

Câu 9: Rút gọn biểu thức: 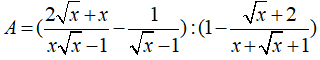Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án với x ≥ 0, x ≠ 1

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án A.

Câu 10: Rút gọn biểu thức: 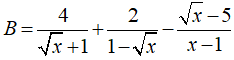Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án với x ≥ 0, x ≠ 1

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Chọn đáp án D.

II. Bài tập tự luận có lời giải

Câu 1: Thực hiện phép tính:

a) (2√2−√3)√2+2√6;

b) 13√27+2√75−√99√11+3√113.

Lời giải:

a) (2√2−√3)√2+2√6

=2√2  .  √2−√3  .  √2+2√6

=4−√6 +2√6

=4+√6 

b) 13√27+2√75−√99√11+3√113

=13  . 3√3+2 . 5√3−√9911+3√43

=√3+10√3−√9+3  .  2√3

=11√3−3+2√3

=13√3−3.

Câu 2: Rút gọn biểu thức:

P=(2√x−2+√x−12√x−x):(√x+2√x−√x−1√x−2)

Lời giải:

ĐKXĐ: x > 0; x ≠ 4.

P=(2√x−2+√x−12√x−x):(√x+2√x−√x−1√x−2)

=[2√x−2−√x−1√x(√x−2)]:(√x+2√x−√x−1√x−2)

=[2√x√x(√x−2)−√x−1√x(√x−2)]:[(√x+2)(√x−2)√x(√x−2)−√x(√x−1)√x(√x−2)]

=2√x−√x+1√x(√x−2):[x−4√x(√x−2)−x−√x√x(√x−2)]

=√x+1√x(√x−2):x−4−x+√x√x(√x−2)

=√x+1√x(√x−2):√x−4√x(√x−2)

=√x+1√x(√x−2).√x(√x−2)√x−4

=√x+1√x−4.

Câu 3: Chứng minh đẳng thức Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Lời giải:

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Câu 4: Rút gọn biểu thức Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Lời giải:

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Câu 5: Rút gọn biểu thức Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Lời giải:

Ta có:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Câu 6:

a) Chứng minh: x2+x√3+1=(x+√32)2+14

b) Tìm giá trị nhỏ nhất của biểu thức x2+x√3+1. Giá trị nhỏ nhất đó đạt được khi x bằng bao nhiêu.

Lời giải:

a) x2+x√3+1=(x+√32)2+14

VP =(x+√32)2+14

=x2+2.x.√32+(√32)2+14=x2+x√3+34+14

=x2+√3x+1 = VT (điều phải chứng minh)

b) Theo câu a ta có:

x2+x√3+1=(x+√32)2+14

Vì (x+√32)2≥0 với mọi x

Do đó (x+√32)2+14≥14

Dấu “=” xảy ra ⇔x+√32=0

⇔x=−√32.

Vậy x2+x√3+1 đạt giá trị nhỏ nhất bằng 14 khi x=−√32

Câu 7: Rút gọn các biểu thức:

a) (2−√2)(−5√2)−(3√2−5)2

b) 2√3a−√75a+a√13,52a−25√300a3 

với a > 0

Lời giải:

a) (2−√2)(−5√2)−(3√2−5)2

=2.(−5√2)+√2.5√2−(3√2)2+2.5.3√2−52

=−10√2+10−18+30√2−25

=(−10√2+30√2)+(10−18−25)

=20√2−33

b) 2√3a−√75a+a√13,52a−25√300a3

=2√3a−√25.3.a+√13,5a22a−25.√100a2.3a=2√3a−5√3a+√274a−25.10|a|.√3a=2√3a−5√3a+√94.√3a−25.10.a.√3a

 (vì a > 0 nên |a| = a)

=2√3a−5√3a+32√3a−4a√3a=(2−5+32)√3a=−32√3a−4a√3a

Câu 8: Cho biểu thức: Q=(1√a−1−1√a):(√a+1√a−2−√a+2√a−1)

a. Rút gọn Q với a > 0, a ≠ 4 và a ≠ 1

b. Tìm giá trị của a để Q dương.

Lời giải:

a) Q=(1√a−1−1√a):(√a+1√a−2−√a+2√a−1)

⇔Q=(√a√a(√a−1)−√a−1√a(√a−1)): 

⇔Q=a−a+1aa−1:      a−1a−2a−1−a−4a−2a−1

⇔Q=1aa−1:a−1−a+4a−2a−1

⇔Q=1a.a−1:3a−2a−1⇔Q=1aa−1.a−2a−13⇔Q=a−23a

 với a > 0, a ≠ 4 và a ≠ 1

b) Để Q dương thì a−23a>0

⇒a−2 và a cùng dấu.

Mà 3a>0 với mọi a thỏa mãn điều kiện

Do đó: a−2>0

⇔a>2⇔a>4

Kết hợp với điều kiện vậy a > 4 thì Q dương.

Câu 9: Tìm x, biết:

a) 4x+20−35+x+439x+45=6

b) 25x−25−152x−19=6+x−1

Lời giải:

a) Điều kiện:

4x+20≥05+x≥09x+45≥0⇔4x≥−20x≥−59x≥−45⇔x≥−5

4x+20−35+x+439x+45=6⇔4.x+5−3x+5+43.9x+5=6⇔2x+5−3x+5+43.3.x+5=6⇔2x+5−3x+5+4x+5=6⇔x+5.2−3+4=6⇔3x+5=6⇔x+5=6:3⇔x+5=2⇔x+5=4 ⇔x=4−5⇔x=−1 (tm)

Vậy x = -1

b) 

Điều kiện:

25x−25≥0x−19≥0x−1≥0⇔25x−1≥0x−1≥0x−1≥0⇒x−1≥0⇔x≥1

25x−25−152x−19=6+x−1⇔25.x−1−152x−19=6+x−1⇔5x−1−52x−1−x−1=6⇔x−1.5−52−1=6⇔32x−1=6⇔x−1=6:32⇔x−1=4 ⇔x−1=16⇔x=16+1 ⇔x=17 (tm)

Vậy x = 17

Câu 10: Với ba số a, b, c không âm, chứng minh bất đẳng thức: a + b + c ≥ ab + bc + ca

Hãy mở rộng kết quả cho trường hợp bốn số, năm số không âm.

Lời giải:

Vì a, b và c không âm nên a;b;c tồn tại.

Ta có: a−b2≥0

⇒a−2ab+b≥0⇔a+b≥2ab⇒a+b2≥ab (1)

Ta có: b−c2≥0

⇒b−2bc+c≥0⇔b+c≥2bc⇒b+c2≥bc (2)

Ta có: c−a2≥0

⇒c−2ca+a≥0⇔c+a≥2ac⇒c+a2≥ac (3)

Cộng vế với vế của (1), (2), (3) ta được:

a+b2+b+c2+c+a2≥ab+bc+ac⇔a+b+b+c+c+a2≥ab+bc+ca⇔2a+2b+2c2≥ab+bc+ca⇔2a+b+c2≥ab+bc+ac⇔a+b+c≥ab+bc+ac

⇒Điều phải chứng minh.

III. Bài tập vận dụng

Câu 1: Chứng minh đẳng thức:

Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Câu 2: Rút gọn biểu thức Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

Câu 3: Cho biểu thức 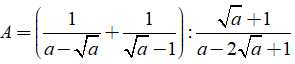Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án và a>0, a ≠ 1 và B = 1

Hãy so sánh A và B

Câu 4: Cho K = 2(1x−1−1x):(x+1x2−x) (với x>0;x≠1)

  1. a) Rút gọn biểu thức K.
  2. b) Tìm x để K = 2012

Câu 5: Cho hai biểu thức A = 4(x+1)25−x và B = (15−xx−25+2x+5):x+1x−5 với x≥0;x≠25

1) Tính giá trị của biểu thức A khi x=9

2) Rút gọn biểu thức B.

Câu 6: Rút gọn biểu thức:

a) \sqrt {14 + 6\sqrt 5 } - \sqrt {14 - 6\sqrt 5 }

b) \sqrt {\left( {\sqrt 5 + 1} \right)\sqrt {6 - 2\sqrt 5 } }

c) \frac{{15}}{{\sqrt 6 - 1}} + \frac{8}{{\sqrt 6 + 2}} + \frac{6}{{3 - \sqrt 6 }} - 9\sqrt 6

Câu 7: Cho biểu thức: A = \frac{{\sqrt x }}{{\sqrt x - 5}} - \frac{{10\sqrt x }}{{x - 25}} - \frac{5}{{\sqrt x + 5}} với x \geqslant 0;x \ne 25

a) Rút gọn biểu thức A.

b) Tính giá trị của A khi x = 9.

c) Tính giá trị của x để biểu thức A = 0,5.

Câu 8: Cho các biểu thức H = \frac{{x - \sqrt[3]{x}}}{{x - 1}} và K = \frac{1}{{\sqrt[3]{x} - 1}} + \frac{1}{{\sqrt[3]{{{x^2}}} + \sqrt[3]{x} + 1}} với x \ne 1

a) Tính giá trị của biểu thức H khi x = 8.

b) Rút gọn biểu thức P = H + K.

c) Tìm giá trị của x để P = 1,5.

Câu 9: Cho biểu thức: A = \frac{{x - 2\sqrt x }}{{x\sqrt x - 1}} + \frac{{\sqrt x + 1}}{{x\sqrt x + x + \sqrt x }} + \frac{{1 + 2x - 2\sqrt x }}{{{x^2} - \sqrt x }}

a) Rút gọn biểu thức A.

b) Tìm x để biểu thức A nhận giá trị là số nguyên.

Câu 10: Rút gọn các biểu thức sau:

a) M = {\left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right)^2}\left( {\frac{{\sqrt x + 1}}{{\sqrt x - 1}} - \frac{{\sqrt x - 1}}{{\sqrt x + 1}}} \right) với x > 0;x \ne 1

b) N = \left( {\frac{{\sqrt x + 1}}{{\sqrt x - 1}} - \frac{{\sqrt x - 1}}{{\sqrt x + 1}} + 4\sqrt x } \right):\frac{{2x\sqrt x }}{{x - 1}} với x \geqslant 0;x \ne 9

c,P = \frac{{x + y}}{{\sqrt x + \sqrt y }}:\left( {\frac{{x + y}}{{x - y}} - \frac{y}{{y - \sqrt {xy} }} + \frac{x}{{\sqrt {xy} + x}}} \right) - \frac{{\sqrt {{{\left( {\sqrt x - \sqrt y } \right)}^2}} }}{2} với y > x > 0

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Căn bậc ba

Chuyên đề Ôn tập chương 1

Chuyên đề Nhắc lại và bổ sung các khái niệm về hàm số

Chuyên đề Hàm số bậc nhất

Chuyên đề Đồ thị của hàm số y = ax + b

Tham khảo các loạt bài Toán 9 khác:

Bài viết cùng lớp mới nhất

Xem thêm
1 2,991 27/08/2022
Tải về
Trang trước
Trang sau  

Xem thêm các chương trình khác: