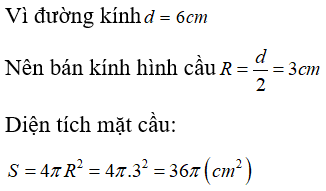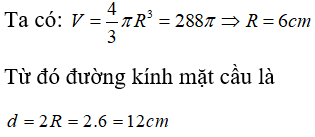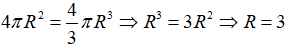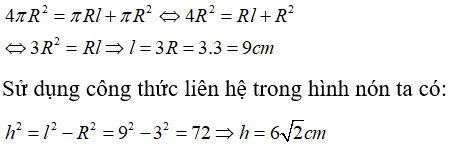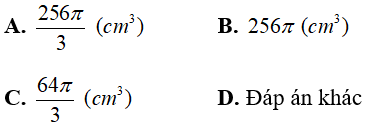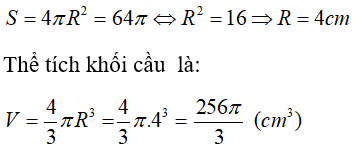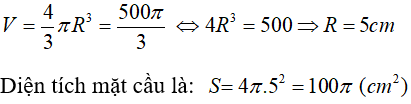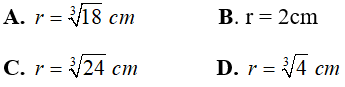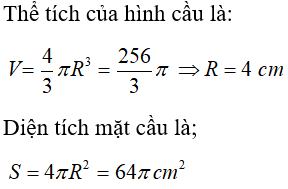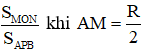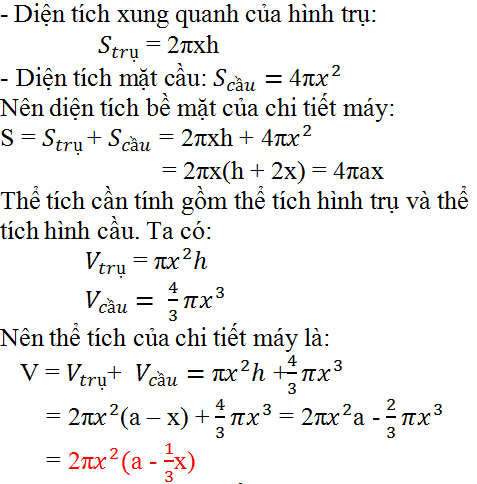Chuyên đề Hình cầu. Diện tích mặt cầu và thể tích hình cầu (2022) - Toán 9

Chuyên đề Hình cầu. Diện tích mặt cầu và thể tích hình cầu - Toán 9

A. Lý thuyết

1. Hình cầu

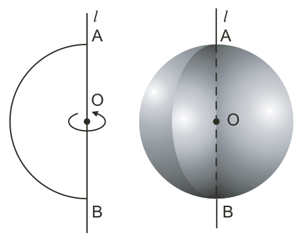
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.

- Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.

- Điểm O được gọi tâm, R là bán kính của hình cầu hay mặt cầu đó.

2. Cắt hình cầu bởi một mặt phẳng

Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn.

Ví dụ 1. Mặt phẳng (P) cắt hình cầu tâm O, bán kính R ta được hình tròn như hình vẽ.

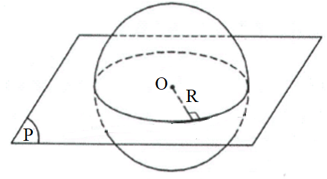
Khi cắt mặt cầu bán kính R bởi một mặt phẳng ta được một đường tròn:

- Đường tròn đó có bán kính R nếu mặt phẳng đi qua tâm (gọi là đường tròn lớn).

- Đường tròn đó có bán kính bé hơn R nếu mặt phẳng không đi qua tâm.

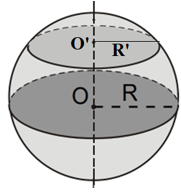
Ví dụ 2. Khi cắt mặt cầu tâm O bán kính R bởi một mặt phẳng ta được:

- Đường tròn tâm O bán kính R: mặt phẳng đi qua tâm.

- Đường tròn tâm O’ bán kính R’: mặt phẳng không đi qua tâm.

Ta có hình vẽ:

3. Diện tích và thể tích của hình cầu

Ví dụ 3. Một hình cầu có thể tích bằng 972π cm³. Tính diện tích của mặt cầu đó.

Lời giải:

Bán kính của mặt cầu đó là:

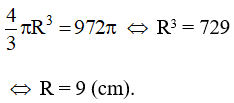
Diện tích của mặt cầu đó là:

S = 4πR² = 4π . 9² = 324π (cm²)

Vậy diện tích của mặt cầu đó là 324π cm².

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Cho hình cầu có đường kính d = 6cm. Diện tích mặt cầu là:

A. 36π (cm²)

B. 9π (cm²)

C. 12π (cm²)

D. 36π (cm²)

Lời giải:

Chọn đáp án A.

Câu 2: Cho mặt cầu có thể tích V = 288π (cm³). Tính đường kính mặt cầu:

A. 6cm

B. 12cm

C. 8cm

D. 16cm

Lời giải:

Chọn đáp án B.

Câu 3: Cho mặt cầu có số đo diện tích bằng số đo thể tích. Tính bán kính mặt cầu:

A. 3

B. 6

C. 9

D. 12

Lời giải:

Từ giả thiết ta có:

Chọn đáp án A.

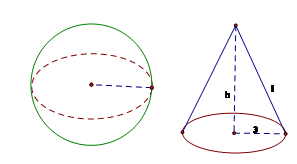
Câu 4: Cho hình cầu có bán kính 3cm. Một hình nón cũng có bán kính đáy bằng 3cm và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón:

A. 3

B. 6√3

C. 72

D. 6√2

Lời giải:

Gọi l là độ dài đường sinh của hình nón.

Vì bán kính hình cầu và bán kính đáy của hình nón bằng nhau nên từ giả thiết ta có:

Chọn đáp án D.

Câu 5: Cho hình cầu có diện tích mặt cầu là 64π (cm²). Tính thể tích khối cầu?

Lời giải:

Ta có:

Chọn đáp án A.

Câu 6: Cho hình cầu có thể tích là: 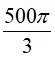,tính diện tích mặt cầu?

A. 50π (cm²)

B. 100π (cm²)

C. 25π (cm²)

D. 75π (cm²)

Lời giải:

Ta có:

Chọn đáp án B.

Câu 7: Cho hình nón có bán kính đáy là 4cm và chiều cao 6cm. Thể tích của một hình cầu bằng thể tích hình nón. Tính bán kính hình cầu?

Lời giải:

Chọn đáp án C.

Câu 8: Cho một hình trụ có bán kính đường tròn đáy là 3cm và chiều cao h = 4cm. Một hình cầu có diện tích bằng diện tích xung quang của hình trụ. Tính bán kính của hình cầu?

A. R = 3cm

B. R = 2cm

C. R = √3 cm

D. R = √6 cm

Lời giải:

Chọn đáp án D.

Câu 9: Cho hình trụ có bán kính đáy là 4cm . Một hình cầu có diện tích mặt cầu bằng diện tích hai đáy của hình trụ.Tính bán kính hình cầu?

A. R = 3cm

B. R = 4cm

C. R = 2√2 cm

D. R = 3√2 cm

Lời giải:

Chọn đáp án C.

Câu 10: Một hình cầu có thể tích là 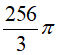 cm³ . Tính diện tích của mặt cầu?

A. 32π

B. 16π

C. 48π

D. 64π

Lời giải:

Chọn đáp án D.

II. Bài tập tự luận có lời giải

Câu 1: Hai hình cầu có hiệu các bán kính bằng 3 cm và hiệu các thể tích bằng 1332π cm³. Tính hiệu các diện tích của hai mặt cầu.

Lời giải:

Gọi bán kính của hình cầu lớn là R và bán kính của hình cầu nhỏ là r.

Ta có R – r = 3 hay R = r + 3.

Nên:

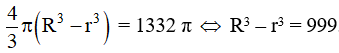
Do đó (r + 3)³ – r³ = 999$\iff$  r² + 3r – 108 = 0.

Giải ra được r₁ = –12 (loại), r₂ = 9 (chọn).

Do đó bán kính hình cầu nhỏ là 9 cm, bán kính hình cầu lớn là 12 cm.

Diện tích mặt cầu lớn là:

S₁ = 4πR² = 4π . 12² = 576π (cm²).

Diện tích mặt cầu nhỏ là:

S₂ = 4πr² = 4π . 9² = 324π (cm²).

Hiệu diện tích hai mặt cầu là:

S = S₁ – S₂ = 576π – 324π = 252π (cm²)

Vậy hiệu diện tích hai mặt cầu là 252π cm².

Câu 2: Một hình cầu có bán kính bằng bán kính đáy của một hình nón. Biết đường sinh của hình nón bằng 12 cm và diện tích xung quanh của hình nón bằng diện tích mặt cầu. Tính thể tích hình cầu.

Lời giải:

Gọi bán kính hình cầu cũng như bán kính đáy hình nón là R.

Diện tích xung quanh hình nón là: πRl = 12πR.

Diện tích mặt cầu là: 4πR².

Vì diện tích xung quanh hình nón bằng diện tích mặt cầu nên:

12πR = 4πR² $\Rightarrow$ R = 3 (cm).

Thể tích hình cầu là: $V=\frac{4}{3}\pi R^3$$=\frac{4}{3}\pi .3^3=36\pi$ (cm³).

Vậy thể tích hình cầu là 36π cm³.

Câu 3: Cho một hình cầu nội tiếp một hình trụ. Chứng minh rằng:

a) Thể tích hình cầu bằng $\frac{2}{3}$ thể tích hình trụ;

b) Diện tích mặt cầu bằng $\frac{2}{3}$ diện tích toàn phần hình trụ.

Lời giải:

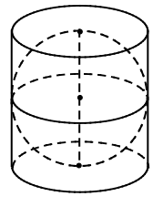
Gọi bán kính hình cầu là R thì bán kính đáy hình trụ là R và chiều cao hình trụ là 2R.

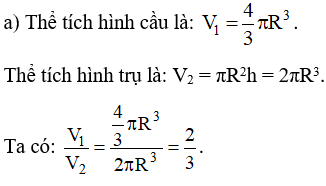
Vậy thể tích hình cầu bằng $\frac{2}{3}$ thể tích hình trụ.

b) Diện tích mặt cầu là: S₁ = 4πR².

Diện tích hình trụ là: S₂ = 2πR(h + R) = 2πR(2R + R) = 6πR².

Ta có: $\frac{S_1}{S_2}=\frac{4\pi R^2}{6\pi R^2}=\frac{2}{3}$.

Vậy diện tích mặt cầu bằng $\frac{2}{3}$ diện tích toàn phần hình trụ.

Câu 4: Cắt một hình trụ hoặc một hình cầu với mặt phẳng vuông góc với trục, ta được hình gì ? Hãy điền vào bảng (chỉ với từ “có”, “không”) (h.104)

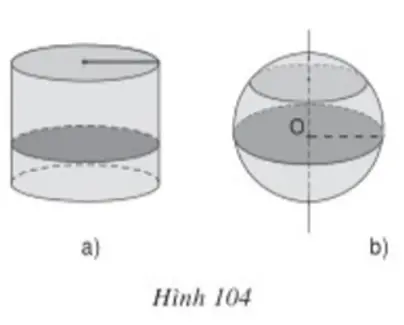
Lời giải:

Mặt cắt	Hình trụ	Hình cầu
Hình chữ nhật	Không	Không
Hình tròn bán kính R	Có	Có
Hình tròn bán kính nhỏ hơn R	Không	Có

Câu 5: Nếu thể tích của một hình cầu là $113\frac{1}{7}c{m}^3$ thì trong các kết quả sau đây, kết quả nào là bán kính của nó, lấy $\pi \approx \frac{22}{7}$ ?

Lời giải

Ta có công thức tính thể tích của hình cầu: $V=\frac{4}{3}\pi R^3\Rightarrow R^3=\frac{3V}{4\pi }$

Mà theo đề bài ta có: V = $113\frac{1}{7}c{m}^3$ và $\pi \approx \frac{22}{7}$

$\Rightarrow R^3\approx \frac{3.113\frac{1}{7}}{4.\frac{22}{7}}\approx 27\Rightarrow R\approx \sqrt[3]{27}=3$ (cm)

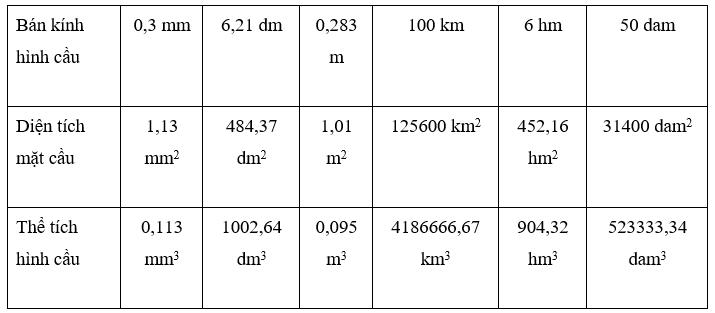
Câu 6: Hãy điền vào các ô trống ở bảng sau:

Bán kính hình cầu	0,3mm	6,21dm	0,283m	100km	6hm	50dam
Diện tích mặt cầu
Thể tích hình cầu

Lời giải:

Cách tính:

Dòng thứ nhất : S = 4πR² . Thay số vào ta được

R = 0,3 mm ⇒ S = 4.3,14. 0,3² = 1,13 (mm²)

R = 6,21 dm ⇒ S = 4.3,14. 6,21² = 484,37 (dm²)

R = 0,283 m ⇒ S = 4.3,14. 0,283² = 1,01 (m²)

R = 100 km ⇒ S = 4.3,14. 100² = 125600 (km²)

R = 6 hm ⇒ S = 4.3,14. 6² = 452,16 (hm²)

R = 50 dam ⇒ S = 4.3,14. 50² = 31400 (dam²)

Dòng thứ hai : V = $\frac{4}{3}$ πR³ thay số vào ta được :

R = 0,3 mm ⇒ V = $\frac{4}{3}$.3,14.0,3³ = 0,113 (mm³)

R = 6,21 dm ⇒ V = $\frac{4}{3}$.3,14. 6,21³ = 1002,64 (dm³)

R = 0,283 m ⇒ V = $\frac{4}{3}$.3,14. 0,283³ = 0,095 (m³)

R = 100 km ⇒ V = $\frac{4}{3}$.3,14. 100³ = 4186666,67 (km³)

R = 6 hm ⇒ V = $\frac{4}{3}$.3,14. 6³ = 904,32 (hm³)

R = 50 dam ⇒ V = $\frac{4}{3}$.3,14. 50³ = 523333,34 (dam³)

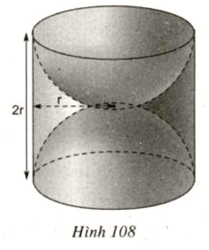
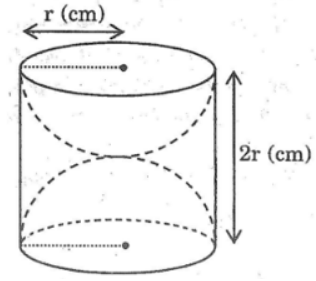
Câu 7: Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị :cm). Người ta khoét rỗng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).

Lời giải:

Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).

Diện tích xung quanh của hình trụ:

    S_xq = 2πrh = 2πr.2r = 4πr² (cm²)

Diện tích mặt cầu:

    S = 4πr²   (cm²)

Diện tích cần tính là:

    4πr² + 4πr² = 8πr²  (cm²) 

Câu 8: Khinh khí cầu của nhà Mông-gôn-fi-ê (Montgolfier)

Ngày 4-6-1783, anh em nhà Mông-gôn-fi-ê (người Pháp) phát minh ra khinh khí cầu dùng không khí nóng. Coi khinh khí cầu này là hình cầu có đường kính 11m. Hãy tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến chữ số thập phân thứ hai).

Hình 109

Lời giải

Diện tích mặt khinh khí cầu là:

S= πd²=3,14.11²=379,94 ( m²)

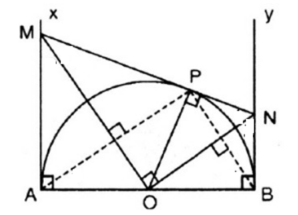
Câu 9: Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.

a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.

b) Chứng minh AM.BN = R²

c) Tính tỉ số 

d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.

Lời giải:

a)

Ta có OM, ON lần lượt là tia phân giác của $\widehat{AOP},\widehat{BOP}$ (tính chất của hai tiếp tuyến cắt nhau).

Mà $\widehat{AOP}$ kề bù với $\widehat{BOP}$ nên suy ra OM vuông góc với ON.

Vậy tam giác MON vuông tại O.

Góc APB là góc nội tiếp chắn nửa đường tròn nên $\widehat{APB}={90}^o$

Do AM là tiếp tuyến với (O) tại A nên $\widehat{MAO}={90}^o$

Do MN là tiếp tuyến với (O) tại P nên $\widehat{MPO}={90}^o$

Tứ giác AOPM có:

$\widehat{MAO}+\widehat{MPO}={90}^o+{90}^o={180}^o$

Do đó, tứ giác AOPM nội tiếp đường tròn 

$\Rightarrow \widehat{PMO}=\widehat{PAO}$ (do là hai góc nội tiếp chắn cung OP)

Xét tam giác MON và tam giác APB  có:

$\widehat{MON}=\widehat{APB}={90}^o$ (chứng minh trên)

$\widehat{PMO}=\widehat{PAO}$ (chứng minh trên)

Do đó, tam giác MON đồng dạng với tam giác APB (góc – góc).

b)

Tam giác MON vuông tại O có đường cao OP 

Áp dụng hệ thức lượng trong tam giác ta có: $O{P}^2=MP.NP$ (1)

Theo tính chất hai tiếp tuyến MN và AM cắt nhau ta có:

MA = MP (2)

Theo tính chất hai tiếp tuyến MN và BN cắt nhau ta có:

NP = NB (3)

Theo (1), (2) và (3) ta có: $O{P}^2=MA.NB\Rightarrow R^2=MA.NB$ (đcpcm)

c)

Theo phần a, tam giác MON và tam giác APB đồng dạng với nhau 

Do đó, tỉ số đồng dạng là: $k=\frac{MN}{AB}\Rightarrow \frac{S_{MON}}{S_{APB}}=k^2=\frac{M{N}^2}{A{B}^2}$ (*)

Theo phần b, ta có: $R^2=MA.NB$

Lại có: $AM=\frac{R}{2}$ nên BN = $R^2:\frac{R}{2}=2R$

Mà: MN = MP + NP = MA + NB = $\frac{R}{2}$ + 2R = $\frac{5}{2}R$

Nên $M{N}^2={\left(\frac{5}{2}R\right)}^2=\frac{25R^2}{4}$ và AB = 2R 

Thay vào (*) ta có: $\frac{S_{MON}}{S_{APB}}=\frac{M{N}^2}{A{B}^2}=\frac{\frac{25R^2}{4}}{{(2R)}^2}=\frac{25}{16}$.

d) 

Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R nên thể tích khối cầu tạo ra là: $V=\frac{4}{3}\pi R^3$.

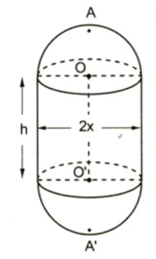
Câu 10: Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm).

a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi và bằng 2a.

b) Với điều kiện ở a), hãy tính diện tích bề mặt và thể tích của chi tiết máy theo x và a.

Hình 111

Lời giải:

a) Ta có: AA’ = AO + OO’ + O’A’

hay 2a = x + h + x

hay 2x + h = 2a.

b) Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là x, chiều cao là h và diện tích mặt cầu có bán kính là x.

III. Bài tập vận dụng

Câu 1: Tính thể tích của một hình cầu biết diện tích của mặt cầu đó bằng 32π.

Câu 2: Một quả bóng có dạng hình cầu thả vào một lọ thuỷ tinh đựng đầy nước dạng hình trụ bán kính đáy là 3cm (đường kính đường tròn lớn hình cầu bằng bán kính đáy hình trụ). Hỏi lượng nước tràn ra là bao nhiêu ?

Câu 3: Tính diện tích của mặt cầu biết thể tích hình câu đó băng 121,5π .

Câu 4: Tính diện tích bề mặt kim loại cần để làm đủ một bồn chứa có dạng hình bên (gồm hai nửa hình cầu và một hình trụ).

Câu 5: Cho một hình cầu có số đo diện tích bằng số đo thể tích. Tính bán kính hình cầu và diện tích mặt cầu đó.

Câu 6: Cho đường tròn (O ; r) ngoại tiếp tam giác đều cạnh a. Tính diện tích mặt cầu và thể tích hình cầu được tạo thành khi quay hình tròn tâm O quanh đường kính của nó theo a.

Câu  7: Một hình nón đặt khít trong nửa hình cầu sao cho đáy của hình nón là hình tròn lớn của hình cầu.

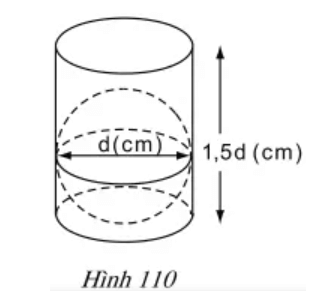
Câu 8: Một hình cầu đường kính d (cm) được đặt vào trong một hình trụ có chiều cao là 1,5d (cm) như hình 110.  Tìm tỉ số $\frac{V_{cau}}{V_{tru}}$ ?

Câu 9: Đổ đầy nước vào mộ dụng cụ để đong có dạng hình nón sau đó đổ hết lượng nước đó vào một hình trụ có bán kính đáy bằng bán kính đáy của hình nón và chiều cao bằng chiều cao của hình nón.Việc làm này lặp lại cho đến khi hình trụ đổ đầy nước thì số lần múc đầy vào hình nón là bao nhiêu?

Câu 10: Một khối gỗ dạng một hình trụ đứng bán kính đường tròn đáy là r (cm) chiều cao 2r(cm) người ta khoét rỗng hai nửa hình cầu như hình bên. Tính diện tích toàn bộ của khối gỗ

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác: