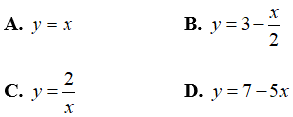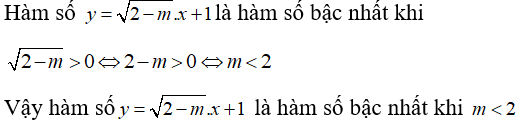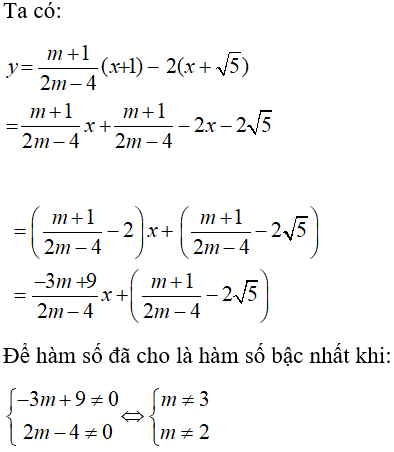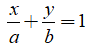Chuyên đề Hàm số bậc nhất (2022) - Toán 9

 Chuyên đề Hàm số bậc nhất - Toán 9

A. Lý thuyết

1. Định nghĩa hàm số bậc nhất

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0.

Chú ý: Khi b = 0 ta có hàm số y = ax (đã học ở lớp 7)

Ví dụ 1. Cho các hàm số:

 y = 3x; y = x + 2; y = $\frac{1}{2}x+2$;

 y = 3x + 1; y = 4x − 1; y = 2 − 3x;

Đây là các hàm số bậc nhất.

2. Tính chất hàm số bậc nhất

Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có các tính chất như sau:

• Đồng biến trên R khi a > 0.

• Nghịch biến trên R khi a < 0.

Ví dụ 2. Cho các hàm số sau: y = 4x – 1, y = − 2x + 1, y = $\frac{1}{2}x+5$; y = $-\sqrt{2}x$. Hàm số nào đồng biến, hàm số nào nghịch biến?

Lời giải:

- Hàm số y = 4x – 1 có a = 4 > 0 nên hàm số này đồng biến trên R.

- Hàm số y = − 2x + 1 có a = − 2 < 0 nên hàm số này nghịch biến trên R.

- Hàm số y = $\frac{1}{2}x+5$ có a = $\frac{1}{2}$  > 0 nên hàm số này đồng biến trên R.

- Hàm số y = $-\sqrt{2}x$ có a = $-\sqrt{2}$  < 0 nên hàm số này nghịch biến trên R.

Vậy hàm số đồng biến là: y = 4x – 1; y = $\frac{1}{2}x+5$;

Hàm số nghịch biến là: y = − 2x + 1; y = $-\sqrt{2}x$.

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số bậc nhất khi:

A. a = 0

B. a < 0

C. a > 0

D. a ≠ 0

Lời giải:

Hàm số bậc nhất là hàm số có dạng: y = ax + b (a ≠ 0)

Chọn đáp án D.

Câu 2: Chọn đáp án đúng nhất. Hàm số y = ax + b là hàm số đồng biến khi:

A. a = 0

B. a < 0

C. a > 0

D. a ≠ 0

Lời giải:

Hàm số bậc nhất y = ax + b xác định với mọi giá trị của thuộc R và có tính chất sau:

• Đồng biến trên R nếu a > 0

• Nghịch biến trên R nếu a < 0

Chọn đáp án C.

Câu 3: Hàm số nào dưới đây là hàm số bậc nhất:

Lời giải:

Theo định nghĩa thì hàm số y = 2x + 1 là hàm số bậc nhất.

Chọn đáp án A.

Câu 4: Hàm số nào dưới đây không là hàm số bậc nhất?

Lời giải:

Theo định nghĩa thì các hàm số 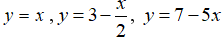 là hàm số 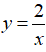bậc nhất.

Hàm số  không là hàm số bậc nhất.

Chọn đáp án C.

Câu 5: Tìm để hàm số 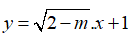 là hàm số bậc nhất:

A. m < 2

B. m > 2

C. m = 2

D. m ≠ 2

Lời giải:

Chọn đáp án A.

Câu 6: Cho hàm số y = (2m -4)x + 100 . Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất?

A. m ≠ 2

B. m ≠ -2

C. m > 2

D. m < -2

Lời giải:

Hàm số bậc nhất là hàm số có dạng: y = ax + b (a ≠ 0)

Để hàm số đã cho là hàm số bậc nhất thì:

2m - 4 ≠ 0 ⇒ 2m ≠ 4 ⇒ m ≠ 2

Chọn đáp án A.

Câu 7: Cho hàm số bậc nhất y = ax + 4. Tìm hệ số a, biết rằng khi x = 1 thì y = 7 ?

A. -3

B. -10

C. 3

D. 10

Lời giải:

Thay x = 1; y = 7 vào y = ax + 4, ta được:

7 = a.1 + 4

Suy ra: a = 3.

Chọn đáp án C.

Câu 8: Cho hàm số 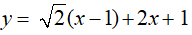 . Cho các khẳng định :

(1). Hàm số đã cho là hàm số bậc nhất

(2). Hàm số đã cho đồng biến trên R.

(3). Giá trị của hàm số tại x = 1 là 3.

Hỏi có bao nhiêu khẳng định đúng?

A. 0

B. 1

C. 2

D. 3

Lời giải:

Ta có:

Chọn đáp án D.

Câu 9: Cho hàm số 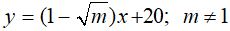 .Tìm m để hàm số đã cho đồng biến trên R.

A. m < 1

B. 0 ≤ m < 1

C. m > 1

D. m ≥ 0

Lời giải:

Chọn đáp án B.

Câu 10: Tìm điều kiện để hàm số 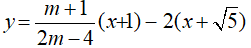 là hàm số bậc nhất?

Lời giải:

Chọn đáp án D.

II. Bài tập tự luận có lời giải

Câu 1: Cho các hàm số sau: y = 3x + 2, y = -x + 1, y = (1/2)x + 1; y = -√3x Hàm số nào đồng biến, hàm số nào nghịch biến ?

Lời giải:

Hàm số đồng biến là: y = 3x + 2; y = (1/2)x + 1

Hàm số nghịch biến là: y = -x + 1; y = -√3x

Câu 2: Xác định m để hàm số y = (m - 1)x + 2 đồng biến

Lời giải:

Hàm số đồng biến khi và chỉ khi m - 1 > 0 ⇒ m > 1

Vậy với m > 1 thì hàm số đã cho đồng biến

Câu 3: Cho hàm số y = 2x2 + 3. Hàm số này có phải hàm số bậc nhất không?

Lời giải:

Vì hàm số bậc nhất có dạng là y = ax + b nên hàm số đã cho y = 2x2 + 3 không phải là hàm số bậc nhất

Câu 4: Cho hàm số y = ax + 1. Biết đồ thị hàm số đi qua điểm A(1;2). Tìm giá trị của a?

Lời giải:

Đồ thị hàm số đi qua điểm A(1;2) nên ta có: 2 = a.1 + 1 ⇒ a = 1

Vậy a = 1 là giá trị cần tìm

Câu 5: Cho hàm số y = ax + 1. Biết đồ thị hàm số đi qua điểm A(1; 2). Tìm giá trị của a.

Lời giải:

Đồ thị hàm số đi qua điểm A(1; 2) nên ta có:

2 = a . 1 + 1

$\iff$ a + 1 = 2

$\iff$ a = 1.

Vậy với a = 1 thì đồ thị hàm số đi qua A(1; 2).

Câu 6: Cho hai hàm số f(x) = 5x – 3 và g(x) = − 4x +1. Tính:

a) $f(-2)-g\left(\frac{1}{2}\right)$;

b) 2f ²(–3) – 3g³(–2).

Lời giải:

a) Ta có: f(−2) = 5. (−2) – 3 = –10 – 3 = –13;

$$\begin{gathered} g\left(\frac{1}{2}\right)=(-4).\frac{1}{2}+1 \\ =-2+1=-1 \end{gathered}$$

Do đó $f(-2)-g\left(\frac{1}{2}\right)$ = –13 – (–1) = –13 + 1 = –12.

Vậy $f(-2)-g\left(\frac{1}{2}\right)=-12$

b) f(−3) = 5. (−3) – 3 = –15 – 3 = –18;

g(−2) = (−4) . (−2) + 1 =8 + 1 = 9.

2f ²(–3) – 3g³(–2) = 2 . (–18)² – 3 . 9³

= 2 . 324 – 3. 729 = 648 − 2187 = −1539.

Vậy 2f ²(–3) – 3g³(–2) = −1539.

Câu 7: Cho các hàm số y = 2mx + m + 1 (1) và hàm số y = (m − 1)x + 3 (2). Xác định m để hàm số (1) đồng biến, hàm số (2) nghịch biến.

Lời giải:

Để hàm số (1) đồng biến, hàm số (2) nghịch biến thì m thỏa mãn:

− Hàm số (1) đồng biến (tức a > 0) hay 2m > 0 $\iff$ m > 0 (1)

− Hàm số (2) nghịch biến (tức a < 0) hay m − 1 < 0 $\iff$ m < 1 (2)

Từ (1) và (2) suy ra: 0 < m < 1.

Vậy để hàm số (1) đồng biến và hàm số (2) nghịch biến thì m thỏa mãn: 0 < m < 1.

Câu 8: Cho hàm số $y=\left(3-\sqrt{2}\right)x+1$

a) Hàm số là hàm đồng biến hay nghịch biến trên ? Vì sao?

b) Tính các giá trị tương ứng của y khi x nhận các giá trị sau:

0; 1; $\sqrt{2}$ ; 3 + $\sqrt{2}$ ; 3 - $\sqrt{2}$

c) Tính các giá trị tương ứng của x khi y nhận các giá trị sau:

0; 1; 8; 2 + $\sqrt{2}$ ; 2 - $\sqrt{2}$

Lời giải:

a) Hàm số $y=\left(3-\sqrt{2}\right)x+1$ là hàm số bậc nhất có a = $3-\sqrt{2}$

Vì 3 - $\sqrt{2}>0$ nên hàm số đã cho đồng biến trên $\mathrm{ℝ}$.

b)

+ Với x = 0 thì

y = f(0) = $\left(3-\sqrt{2}\right).0+1=1$

+ Với x = 1 thì

y = f(1) = $\left(3-\sqrt{2}\right).1+1$

  $=3-\sqrt{2}+1=4-\sqrt{2}$

+ Với x = $\sqrt{2}$ thì

y = f $\left(\sqrt{2}\right)$ = $\left(3-\sqrt{2}\right).\sqrt{2}+1$

  $=3\sqrt{2}-2+1=3\sqrt{2}-1$

+ Với x = 3 + $\sqrt{2}$ thì

y = $f\left(3+\sqrt{2}\right)=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)+1$

  $=9-2+1=8$

+ Với x = 3 - $\sqrt{2}$ thì

y = $f\left(3-\sqrt{2}\right)=\left(3-\sqrt{2}\right)\left(3-\sqrt{2}\right)+1$

  $=9-3\sqrt{2}-3\sqrt{2}+2+1=12-6\sqrt{2}$

c)

+ Với y = 0 $\Rightarrow \left(3-\sqrt{2}\right).x+1=0$

$$\begin{gathered} \iff \left(3-\sqrt{2}\right)x=-1 \\ \iff x=\frac{-1}{3-\sqrt{2}} \\ =\frac{-1.\left(3+\sqrt{2}\right)}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)} \\ =\frac{-3-\sqrt{2}}{3^2-{\left(\sqrt{2}\right)}^2} \\ =\frac{-3-\sqrt{2}}{9-2} \\ =\frac{-3-\sqrt{2}}{7} \end{gathered}$$

+ Với y = 1 $\Rightarrow \left(3-\sqrt{2}\right).x+1=1$

$$\begin{gathered} \iff \left(3-\sqrt{2}\right)x=0 \\ \iff x=0 \end{gathered}$$

+ Với y = 8 $\Rightarrow \left(3-\sqrt{2}\right).x+1=8$

$$\begin{gathered} \iff \left(3-\sqrt{2}\right)x=7 \\ \iff x=\frac{7}{3-\sqrt{2}} \\ =\frac{7.\left(3+\sqrt{2}\right)}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)} \\ =\frac{7.\left(3+\sqrt{2}\right)}{3^2-{\left(\sqrt{2}\right)}^2} \\ =\frac{7.\left(3+\sqrt{2}\right)}{9-2} \\ =\frac{7.\left(3+\sqrt{2}\right)}{7}=3+\sqrt{2} \end{gathered}$$

+ Với y = $2+\sqrt{2}$

$$\begin{gathered} \Rightarrow \left(3-\sqrt{2}\right).x+1=2+\sqrt{2} \\ \iff \left(3-\sqrt{2}\right)x=1+\sqrt{2} \\ \iff x=\frac{1+\sqrt{2}}{3-\sqrt{2}} \\ =\frac{\left(1+\sqrt{2}\right).\left(3+\sqrt{2}\right)}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)} \\ =\frac{3+\sqrt{2}+3\sqrt{2}+2}{3^2-{\left(\sqrt{2}\right)}^2} \\ =\frac{3+\sqrt{2}+3\sqrt{2}+2}{7} \\ =\frac{5+4\sqrt{2}}{7} \end{gathered}$$

+ Với y = $2-\sqrt{2}$

$\Rightarrow \left(3-\sqrt{2}\right).x+1=2-\sqrt{2}$

$$\begin{gathered} \iff x=\frac{1-\sqrt{2}}{3-\sqrt{2}} \\ =\frac{\left(1-\sqrt{2}\right).\left(3+\sqrt{2}\right)}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)} \\ =\frac{3+\sqrt{2}-3\sqrt{2}-2}{3^2-{\left(\sqrt{2}\right)}^2} \\ =\frac{3+\sqrt{2}-3\sqrt{2}-2}{7} \\ =\frac{1-2\sqrt{2}}{7} \end{gathered}$$

Câu 9: Một hình chữ nhật có kích thước là 25cm và 40cm. Người ta tăng mỗi kích thước của hình chữ nhật thêm x cm. Gọi S và P theo thứ tự là diện tích và chu vi hình chữ nhật mới tính theo x.

a) Hỏi rằng các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao?

b) Tính các giá trị tương ứng của P khi x nhận các giá trị (tính theo đơn vị cm) sau: 0; 1; 1,5; 2,5; 3,5

Lời giải:

Gọi hình chữ nhật ban đầu là: ABCD

Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật AB’C’D’ có chiều dài AB’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.

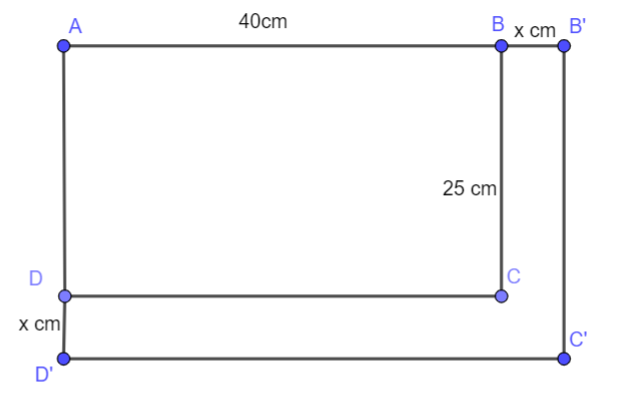
a) Diện tích hình chữ nhật mới:

S = (40 + x)(25 + x)

= 1000 + 25x + 40x + $x^2$

=1000 + 65x + $x^2$(cm²)

S không phải là hàm số bậc nhất đối với x vì có bậc của biến số x là bậc hai.

Chu vi hình chữ nhật mới:

P = 2.[(40 + x) + (25 + x)]

= 2.(65 + 2x) = 4x + 130 (cm)

P là hàm số bậc nhất đối với x

có hệ số a = 4, hệ số b = 130.

b) Các giá trị tương ứng của P:

+ Với x = 0 thì P = 4.0 + 130 = 130cm

+ Với x = 1 thì P = 4.1 +130 = 134cm

+ Với x = 1,5 thì P = 4.1,5 + 130

= 6 + 130 = 136cm

+ Với x = 2,5 thì P = 4.2,5 + 130

= 10 + 130 = 140cm

+ Với x = 3,5 thì P = 4.3,5 + 130

= 14 + 130 = 144cm

Câu 10: Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b xét xem hàm số nào đồng biến? Hàm số nào nghịch biến?

a) y = 3 – 0,5x;

b) y = -1,5x;

c) y = 5 - 2;

d) y = $\left(\sqrt{2}-1\right)x$ + 1;

e) y = $\sqrt{3}\left(x-\sqrt{2}\right)$;

f) y + $\sqrt{2}$ = x - $\sqrt{3}$;

Lời giải:

+ Hàm số a) y = 3 – 0,5x = - 0,5x + 3 là hàm số bậc nhất vì nó có dạng

y = ax + b với

a = -0,5; b = 3.

Hàm số y = 3 – 0,5x là hàm số nghịch biến vì a = -0,5.

+ Hàm số b) y = -1,5x = -1,5x + 0 là hàm số bậc nhất vì nó có dạng

y = ax + b với

a = -1,5; b = 0.

Hàm số y = -1,5x là hàm số nghịch biến vì

a = -1,5.

+ Hàm số c) y = 5 – 2$x^2$ không là hàm số bậc nhất vì nó không có dạng

y = ax + b.

+ Hàm số d) y = $\left(\sqrt{2}-1\right)x+1$ là hàm số bậc nhất vì nó có dạng y = ax + b với

a = $\sqrt{2}-1$; b = 1.

Hàm số y = $\left(\sqrt{2}-1\right)x+1$ là hàm số đồng biến vì a = $\sqrt{2}-1$ > 0 .

+ Hàm số e)

y = $\sqrt{3}\left(x-\sqrt{2}\right)=\sqrt{3}x-\sqrt{6}$ 

là hàm số bậc nhất vì nó có dạng y = ax + b với a = $\sqrt{3}$; b = - $\sqrt{6}$.

Hàm số y = $\sqrt{3}x-\sqrt{6}$ là hàm số đồng biến vì a = $\sqrt{3}$ > 0 .

+ Hàm số f) $y+\sqrt{2}=x-\sqrt{3}\Rightarrow y=x-\sqrt{2}-\sqrt{3}$ là hàm số bậc nhất vì nó có dạng y = ax + b với a = 1; b = $-\sqrt{2}-\sqrt{3}$.

Hàm số y = x $-\sqrt{2}-\sqrt{3}$ là hàm số đồng biến vì a = 1 > 0 .

III. Bài tập vận dụng

Câu 1: Xác định đường thẳng đi qua hai điểm A và B biết A(-20; 0) và B(0; 1)

Câu 2: Chứng minh rằng nếu một đường thẳng không đi qua gốc tọa độ, cắt trục hoành tại điểm có hoành độ bằng a, cắt trục tung tại điểm có tung độ bằng b thì đường thẳng đó có phương trình là 

Câu 3: Cho hàm số y = (m - 2)x + m + 2. Xác định m, biết:

    a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -2.

    b) Đồ thị hàm số đi qua gốc tọa độ.

Câu 4: Cho đường thẳng (d): y = -2x + 3. Tìm m để đường thẳng (d) đi

qua điểm A (-m; -3).

Câu 5: Chứng minh rằng đường thẳng (d): (m + 2)x + y + 4m - 3 = 0

luôn đi qua một điểm cố định với mọi giá trị của m.

Câu 6: Cho hàm số  y = ( m – 2).x + n   (d’)  trong đó m, n là tham số

a) Tìm m, n để (d’) đi qua hai điểm A(1 ; – 2) ; B(3 ; – 4 )

b) Tìm m, n để (d’) cắt trục tung tại  điểm M có tung độ  và cắt trục hoành tại điểm N có hoành độ

Câu 7: Cho hai hàm số 

    a) Tìm tập xác định của hàm số đã cho

    b) Tính f(2); f(1/2), g(0), g(1), g(1/2)

Câu 8: Cho hàm số y = -mx + m - 3. Biết f(-2) = 6. Tính f(-3)

Câu 9: Xác định tính đồng biến, nghịch biến của các hàm số sau:

    a) y = f(x) = (1 - √2)x + 1, với x ∈ R

    b) 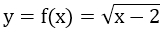 với x ≥ 2

    c) y = f(x) = x² + 2,với x < 0

Câu 10: Cho hàm số y = (2m + 1)x - m + 3

 a) Tìm m biết đồ thị đi qua điểm A(-2; 3)

 b) Tìm điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị của m

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Đồ thị của hàm số y = ax + b

Chuyên đề Đường thẳng song song và đường thẳng cắt nhau

Chuyên đề Hệ số góc của đường thẳng y = ax + b

Chuyên đề Ôn tập chương 2

Chuyên đề Một số hệ thức về cạnh và đường cao trong tam giác vuông