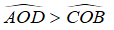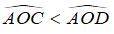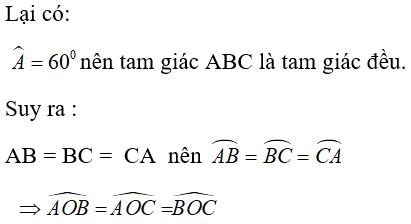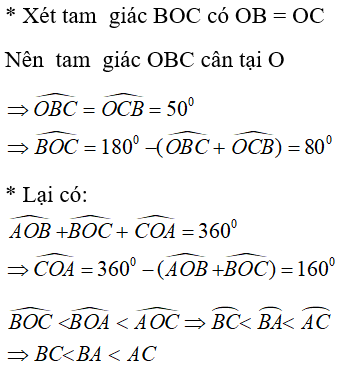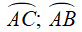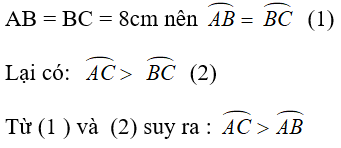Chuyên đề Liên hệ giữa cung và dây (2022) - Toán 9

Chuyên đề Liên hệ giữa cung và dây - Toán 9

A. Lý thuyết

1. Định lí 1

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

- Hai cung bằng nhau căng hai dây bằng nhau.

- Hai dây bằng nhau căng hai cung bằng nhau.

Ví dụ 1. Cho đường tròn (O) như hình vẽ.

Trong hình vẽ $\stackrel{⏜}{AB}=\stackrel{⏜}{CD}$ () nên AB = CD.

2. Định lí 2

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

- Cung lớn hơn căng dây lớn hơn.

- Dây lớn hơn căng cung lớn hơn.

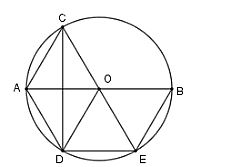
Ví dụ 2. Cho đường tròn (I) như hình vẽ.

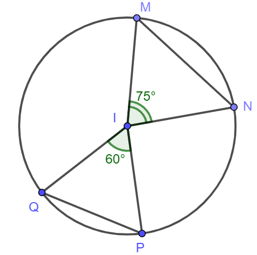
Trong hình vẽ :

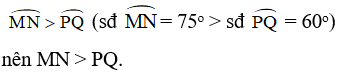
3. Bổ sung

Trong một đường tròn:

- Hai cung bị chắn giữa hai dây song song thì bằng nhau.

- Đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.

- Đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.

- Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.

B. Bài tập

I. Bài tập trắc nghiệm

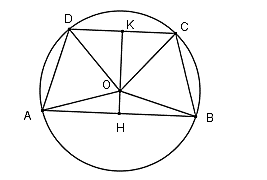
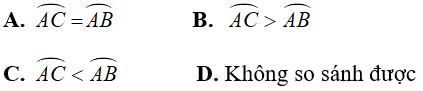
Câu 1: Cho đường tròn (O) có hai dây AB, CD song song với nhau. Kết luận nào sau đây là đúng?

A. AD > BC

B. Số đo cung AD bằng số đo cung BC

C. AD < BC

D. 

Lời giải:

Qua O kẻ đường thẳng vuông góc với AB và CD, cắt AB, CD lần lượt tại H và K.

Phương án A, C, D sai, B đúng

Chọn đáp án B

Câu 2: Chọn khẳng định đúng. Cho đường tròn (O) có dây cung AB > CD khi đó

A. Cung AB lớn hơn cung CD

B. Cung AB nhỏ hơn cung CD

C. Cung AB bằng cung CD

D. Số đo cung AB bằng hai lần số đo cung BC

Lời giải:

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau

+ Cung lớn hơn căng dây lớn hơn

+ Dây lớn hơn căng cung lớn hơn

Nên dây AB > CD thì cung AB lớn hơn cung CD

Chọn đáp án A

Câu 3: Cho đường tròn (O) đường kính AB và một cung AC có số đo nhỏ hơn 90°. Vẽ dây CD vuông góc với AB và dây DE song song với AB . Chọn kết luận sai?

A. AC = BE

B. Số đo cung AD bằng số đo cung BE

C. Số đo cung AC bằng số đo cung BE

D. 

Lời giải:

Chọn đáp án D

Câu 4: Chọn khẳng định đúng.

A. Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.

B. Trong một đường tròn, đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.

C. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì song song với dây căng cung ấy

D. Trong một đường tròn, hai đường kính luôn vuông góc với nhau

Lời giải:

+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy

+ Trong một đường tròn, đường kính đi qua trung điểm của một dây (không qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy

+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông với dây căng cung ấy và ngược lại

Chọn đáp án A.

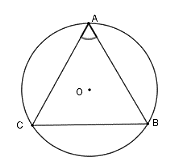
Câu 5: Cho tam giác ABC cân tại A có A^= 66° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung nào là cung lớn nhất?

A. AB

B. AC

C. BC

D. AB, AC

Lời giải:

nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có:

Chọn đáp án C.

Câu 6: Cho nửa đường tròn (O) đường kính AB. Lấy các điểm C và D trên nửa đường tròn sao cho: 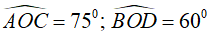. Tìm khẳng định sai?

CD < BD < CA

Lời giải:

Ta có:

Chọn đáp án D.

Câu 7: Cho đường tròn (O) ngoại tiếp tam giác ABC biết rằng A^= 60° và AB = BC .Tìm khẳng định sai ?

Lời giải:

Ta có: AB = BC nên tam giác ABC cân tại B.

Chọn đáp án A.

Câu 8: Cho tam giác ABC nội tiếp đường tròn (O) sao cho 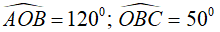 biết rằng A và C nằm khác phía so với đường thẳng OB. Tìm mệnh đề sai ?

Lời giải:

Chọn đáp án C.

Câu 9: Cho nửa đường tròn (O) đường kính AB, điểm C và D nằm trên nửa đường tròn sao cho 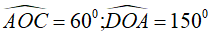 và tia OC nằm giữa hai tia OA và O

D. Tìm khẳng định đúng

Lời giải:

Chọn đáp án A.

Câu 10: Cho tam giác ABC nội tiếp đường tròn tâm (O), biết rằng AB = BC = 8cm và  . So sánh hai cung 

Lời giải:

Ta có:

Chọn đáp án B.

II. Bài tập tự luận có lời giải

Câu 1: Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O). Biết $\widehat{A}={70}^o$. Hãy so sánh các cung nhỏ AB, AC và BC.

Lời giải:

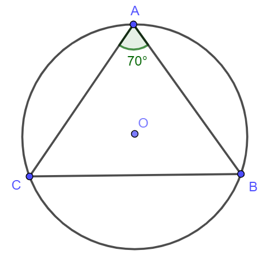
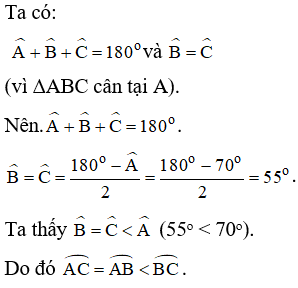
Câu 2: Cho đường tròn tâm O đường kính AB. Từ A và B vẽ hai dây cung AC và BD song song vs nhau. Qua O vẽ đường thẳng vuông góc AC tại M và BD tại N. So sánh hai cung AC và BD.

Lời giải:

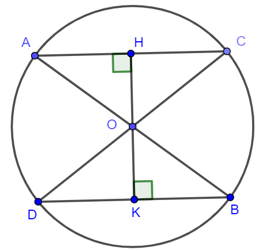
a) Chứng minh rằng OH < OK.

b) So sánh hai cung nhỏ BD và BC.

a)

Xét tam giác ABC có:

BC > AB – AC (bất đẳng thức trong tam giác)

Mà AC = AD (gt)

 BC > AB – AD

BC > BD

Xét đường tròn (O) ta có: BC > BD

Mà từ O lần lượt hạ các đường vuông góc OH, OK xuống BC và BD (gt)

Do đó, OH, OK lần lượt là khoảng cách từ tâm đến BC, BD

 OH < OK (dây lớn hơn gần tâm hơn).

b)

Ta có: BC > BD

  $\Rightarrow$$\stackrel{⏜}{BC}>\stackrel{⏜}{BD}$ (dây lớn hơn căng cung lớn hơn).

a) $\stackrel{⏜}{AE}=\stackrel{⏜}{FB}$ ;

b) $\stackrel{⏜}{AE}<\stackrel{⏜}{EF}$ .

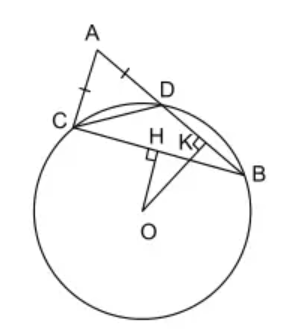
a)

Xét tam giác OAB có:

OA = OB (cùng bằng bán kính đường tròn (O))

Do đó, tam giác OAB cân tại O

$\Rightarrow \widehat{OAB}=\widehat{OBA}$

Xét tam giác OAC và tam giác OBD có:

OA = OB (cùng bằng bán kính đường tròn (O))

 $\widehat{OAB}=\widehat{OBA}$ (cmt)

AC = BD (gt)

Do đó, tam giác OAC  bằng tam giác OBD (cạnh – góc – cạnh)

 $\Rightarrow \widehat{O_1}=\widehat{O_2}$ (1)

Mặt khác, ta có:

Góc  là góc ở tâm chắn cung nhỏ AE$\Rightarrow$ sđ$\stackrel{⏜}{AE}=\widehat{O_1}$  (2)

Góc  là góc ở tâm chắn cung nhỏ BF$\Rightarrow$ sđ$\stackrel{⏜}{BF}=\widehat{O_2}$  (3)

Từ (1), (2), (3) ta suy ra: $sđ\stackrel{⏜}{AE}=sđ\stackrel{⏜}{BF}$  nên $\stackrel{⏜}{AE}=\stackrel{⏜}{BF}$ .

b)

Tam giác OAC bằng tam giác OBD (chứng minh phần a)

⇒ OC = OD

Do đó, tam giác OCD cân tại O

 $\Rightarrow \widehat{OCD}=\widehat{ODC}<{90}^o$

Mà $\widehat{ODC}+\widehat{CDF}={180}^o$  (hai góc kề bù)

$\Rightarrow \widehat{CDF}>{90}^o$

Xét tam giác CDF có:

$\widehat{CDF}>{90}^o$

⇒ CF > CD

Mà CD = AC

Nên CF > AC

Xét tam giác OAC và tam giác OCF có:

OA = OF (cùng bằng bán kính đường tròn (O))

OC là cạnh chung

AC < CF   (chứng minh trên)

$\Rightarrow \widehat{O_1}<\widehat{O_3}$ (hai tam giác có 2 cạnh bằng nhau từng đôi một, cạnh thứ ba không bằng nhau thì đối diện cạnh lớn hơn là góc lớn hơn)

Mà:

Góc $O_1$  là góc ở tâm chắn cung nhỏ AE $\Rightarrow$ sđ$\stackrel{⏜}{AE}=\widehat{O_1}$  

Góc $O_3$  là góc ở tâm chắn cung nhỏ EF $\Rightarrow$ sđ$\stackrel{⏜}{EF}=\widehat{O_3}$

Do đó:   $sđ\stackrel{⏜}{AE}<sđ\stackrel{⏜}{EF}$$\Rightarrow \stackrel{⏜}{AE}<\stackrel{⏜}{EF}$.

a) Hai cung nhỏ CF và BD bằng nhau.

b) Hai cung nhỏ BF và DE bằng nhau.

c) DE = BF.

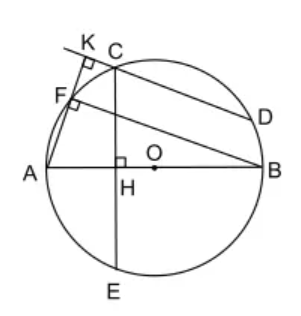
a)

Tam giác AFB nội tiếp đường tròn (O) có AB là đường kính nên tam giác AFB vuông tại F

$\Rightarrow \widehat{AFB}={90}^o$

$\Rightarrow BF\perp AK$ tại F

Mà AK vuông góc với CD (gt)

$\Rightarrow BF\parallel CD$

 $\Rightarrow \stackrel{⏜}{BD}=\stackrel{⏜}{CF}$ (hai cung chắn giữa hai dây song song thì bằng nhau).

b)

Đường kính AB vuông góc với CE tại H nên H là trung điểm của CE

Do đó, C đối xứng với E qua trục AB

$\Rightarrow BC=BE$

 $\Rightarrow \stackrel{⏜}{BC}=\stackrel{⏜}{BE}$ (hai dây cung bằng nhau căng hai cung bằng nhau)

Mà $\stackrel{⏜}{BD}=\stackrel{⏜}{CF}$  (cmt)

$\Rightarrow \stackrel{⏜}{BC}+\stackrel{⏜}{CF}=\stackrel{⏜}{BE}+\stackrel{⏜}{BD}$

$\Rightarrow \stackrel{⏜}{BF}=\stackrel{⏜}{DE}$

c)

Có: $\stackrel{⏜}{BF}=\stackrel{⏜}{DE}$  (cmt)

Do đó, BF = DE (hai cung bằng nhau căng hai dây bằng nhau).

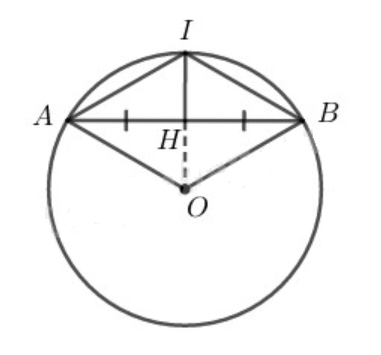
Theo đề bài ta có: $\stackrel{⏜}{IA}=\stackrel{⏜}{IB}$

$\Rightarrow$ IA = IB (hai cung bằng nhau căng hai dây bằng nhau)

Do đó, I nằm trên đường trung trực của AB (1)

Mặt khác, OA = OB (cùng bằng bán kính đường tròn (O))

Do đó, O nằm trên đường trung trực của AB (2)

Từ (1) và (2) ta suy ra OI là đường trung trực của AB

Mà H là trung điểm của AB, do đó H thuộc OI

Do đó, ba điểm I, H, O thẳng hàng.

Vậy đường thẳng IH đi qua tâm O của đường tròn.

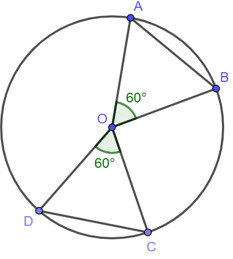
Vì không phải là cung lớn nên hai cung đó có thể là cung nhỏ hoặc cung nửa đường tròn.

Ta có cung nửa đường tròn có số đo bằng 180°  và dây cung bằng 2R, cung nửa đường tròn này gấp ba lần cung tròn 60° (có góc ở tâm bằng 60°)

Tam giác tạo bởi dây căng cung và hai bán kính đi qua hai đầu mút của cung 60° là một tam giác đều nên dây căng cung bằng bán kính R. Vậy nửa đường tròn và cung 60° thỏa mãn bài toán.

Ta có: $\widehat{AOB}={80}^o$ , $\widehat{BOC}={120}^o$

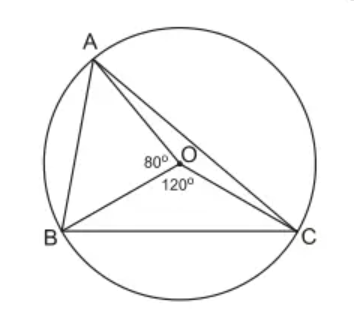
$\Rightarrow \widehat{AOC}={360}^o-{80}^o-{120}^o={160}^o$

Góc AOB là  góc nội tiếp chắn cung nhỏ AB $\Rightarrow$ sđ$\stackrel{⏜}{AB}=\widehat{AOB}={80}^o$

Góc BOC là  góc nội tiếp chắn cung nhỏ BC $\Rightarrow$ sđ$\stackrel{⏜}{BC}=\widehat{BOC}={120}^o$

Góc AOC là  góc nội tiếp chắn cung nhỏ AC $\Rightarrow$ sđ$\stackrel{⏜}{AC}=\widehat{AOC}={160}^o$

$\Rightarrow \stackrel{⏜}{AB}<\stackrel{⏜}{BC}<\stackrel{⏜}{AC}$

$\Rightarrow AB<BC<AC$

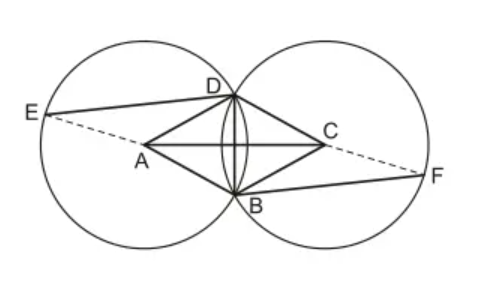
Ta có (A; AD) và (C; CB) có bán kính AD = CB là cạnh của hình thoi ABCD nên hai đường tròn đó bằng nhau.

Ta có: AD = AB = CD = CB

Do đó, (A; AD) và (C; CB) cắt nhau tại B và D

Mặt khác: DE // BF (gt)

 $\Rightarrow \widehat{EDB}=\widehat{FBD}$ (so le trong)

 $\Rightarrow \widehat{EDA}+\widehat{ADB}=\widehat{FBC}+\widehat{CBD}$(1)

Do ABCD là hình thoi nên ta có:

$\widehat{ADC}=\widehat{ABC}$

DB là phân giác của $\widehat{ADC}$  và$\widehat{ABC}$

 $\Rightarrow \widehat{ADB}=\widehat{CBD}$(2)

Từ (1) và (2)  $\Rightarrow \widehat{EDA}=\widehat{FBC}$(3)

Xét tam giác ADE có:

AD = AE (cùng bằng bán kính đường tròn (A))

Do đó, tam giác ADE cân tại A

 $\Rightarrow \widehat{EAD}={180}^o-2\widehat{EDA}$(4)

Xét tam giác CBF có:

CB = CF (cùng bằng bán kính đường tròn (C))

Do đó, tam giác CBF cân tại C

 $\Rightarrow \widehat{BCF}={180}^o-\widehat{FBC}$(5)

Từ (3), (4) và (5) ta suy ra: $\widehat{EAD}=\widehat{BCF}$

Mà ta có:

sđ$\stackrel{⏜}{DE}=\stackrel{⏜}{EAD}$  (góc ở tâm chắn cung)

sđ$\stackrel{⏜}{BF}=\widehat{BCF}$ (góc ở tâm chắn cung)

Và (A; AD) và (C; CB) bằng nhau

$\Rightarrow \stackrel{⏜}{DE}=\stackrel{⏜}{BF}$

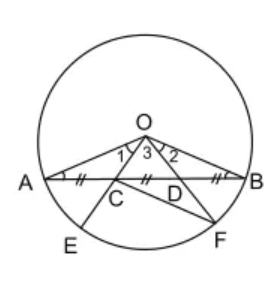
Câu 10: Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M. Biết $\widehat{AMB}=40°$

a) Tính $\widehat{AOM}$ và $\widehat{AMO}$ .

b) Tính số đo cung $\stackrel{⏜}{AB}$ nhỏ và số đo cung $\stackrel{⏜}{AB}$ lớn.

Lời giải:

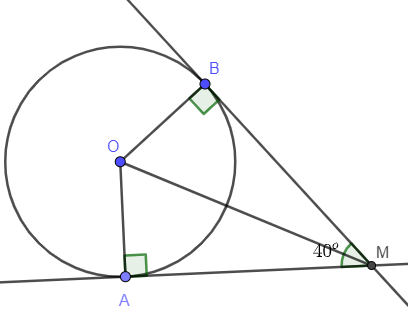
a) Vì AM và BM là hai tiếp tuyến cắt nhau tại M

=> OM là tia phân giác của $\widehat{AMB}$  (tính chất hai tiếp tuyến cắt nhau).

$\Rightarrow \widehat{AMO}=\widehat{BMO}=\frac{\widehat{AMB}}{2}=\frac{40°}{2}=20°$

Vì AM là tiếp tuyến của đường tròn $\Rightarrow OA\perp AM$  (tính chất)

$\Rightarrow \widehat{OAM}=90°$

Xét tam giác AOM có:

$\widehat{OAM}+\widehat{AMO}+\widehat{AOM}=180°$ (định lí tổng ba góc trong một tam giác)

$\iff 90°+20°+\widehat{AOM}=180°$

$\iff \widehat{AOM}=180°-90°-20°$

$\iff \widehat{AOM}=70°$

b) Vì AM và BM là hai tiếp tuyến cắt nhau tại M

=> OM là tia phân giác $\widehat{AOB}$  (tính chất)

$\Rightarrow \widehat{AOM}=\widehat{BOM}=\frac{\widehat{AOB}}{2}$

$\Rightarrow \widehat{AOB}=2\widehat{AOM}\iff \widehat{AOB}=2.70°=140°$

Ta có: $\widehat{AOB}$ là góc ở tâm chắn cung nhỏ $\stackrel{⏜}{AB}$

$\Rightarrow \widehat{AOB}$ = sđ $\stackrel{⏜}{AB}$ nhỏ (định lí góc ở tâm)

=> sđ $\stackrel{⏜}{AB}$ nhỏ = $140°$

Số đo $\stackrel{⏜}{AB}$ lớn là:

$360°$ - sđ $\stackrel{⏜}{AB}$ nhỏ = $360°-140°=220°$

III. Bài tập vận dụng

Câu 1: Cho đoạn thẳng AB = 13cm, trên đó lấỵ C sao cho AC = 9cm. Trên tia Cx ⊥ AB, lấy D sao cho CD = 6cm. Vẽ đường tròn tâm O, đường kính BA.

a) Chứng minh rằng : D thuộc đường tròn đường kính AB.

b) So sánh 2 cung nhỏ AD và BD.

c) Gọi E là trung điểm của AD, P là trung điểm của BD. Tia OE cắt (O) tại Q, tia OP cắt (O) tại M. Tính số đo của cung QM.

Câu 2: Cho đường tròn (O) đường kính AB, C là một điểm tuỳ ý  trên cung M, N là điểm chính giữa của cung AC và CB. OM cắt AC tại I, ON cắt CB tại K.

a) Tứ giác OICK là hình gì ?

b) Xác định vị trí của c để OICK là hình vuông.

Câu 3: Các nhận xét sau đây đúng hay sai ? Điền dấu (x) vào chỗ … tương ứng.

Trong một đường tròn, 2 dây bằng nhau căng 2 cung bằng nhau. …..

Trong một đường tròn, 2 cung bằng nhau thì căng 2 dây bằng nhau. …..

Câu 4:Trên đường tròn tâm O, lấy 2 điểm B, c sao cho số đo cung BC bằng 120°. Lấy A thuộc cung lớn BC. Gọi D là điểm chính giữa cung AC, E là điểm chính giữa cung AB. Số đo cung DAE bằng bao nhiêu?

Câu 5: Cho tam giác ABC nội tiếp đường tròn, biết góc A = 45°, góc B = 60° . So sánh các cung nhỏ AB, AC , BC .

Câu 6: Chỉ dùng compa và thước kẻ hãy nêu cách vẽ AABC đều nội tiếp (O; 4cm) cho trước.

Câu 7: Cho (O) và 2 dây của nó là AB và CD sao cho AB // CD.

a) Chứng minh rằng : AC = BD.

b) So sánh cung AC và cung BD rồi rút ra nhận xét về 2 cung bị chắn giữa 2 dây song song.

Câu 8:

Cho (O ; R), vẽ liên tiếp 3 dây AB, BC, CD bằng nhau và bằng R.

a) Chứng minh ABCD là hình thang cân.

b) Gọi M, N lần lượt là điểm chính giữa các cung nhỏ AB, CD. OM, ON cắt AB, CD thứ tự tại P, Q. Tính PQ, MN theo R.

Câu 9: Trong một hình tròn có bán kính bằng 1, ta lấy 13 điểm. Chứng minh rằng luôn có ít nhất 3 điểm tạo thành một tam giác có chu vi bé hơn hoặc bằng 3.

Câu 10: Cho nửa đường tròn (O), đường kính AB và C là điểm chính giữa của nửa đường tròn. Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho $\stackrel{⏜}{CM}=\stackrel{⏜}{BN}$ . Chứng minh:

a) AM = CN.

b) MN = CA = CB.

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Góc nội tiếp

Chuyên đề Góc tạo bởi tia tiếp tuyến và dây cung

Chuyên đề Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn

Chuyên đề Cung chứa góc

Chuyên đề Tứ giác nội tiếp