Chuyên đề Hàm số bậc nhất mới nhất - Toán 9

Mục lục Chuyên đề Toán 9 Chương 2: Hàm số bậc nhất

Chuyên đề Nhắc lại và bổ sung các khái niệm về hàm số

Xem chi tiết

Chuyên đề Hàm số bậc nhất

Xem chi tiết

Chuyên đề Đồ thị của hàm số y = ax + b

Xem chi tiết

Chuyên đề Đường thẳng song song và đường thẳng cắt nhau

Xem chi tiết

Chuyên đề Hệ số góc của đường thẳng y = ax + b

Xem chi tiết

Chuyên đề Ôn tập chương 2

Xem chi tiết

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chương 1: Hệ thức lượng trong tam giác vuông

Chương 2: Đường tròn

Chương 3: Hệ hai phương trình bậc nhất hai ẩn

Chương 4: Hàm số y = ax^2 (a khác 0). Phương trình bậc hai một ẩn

Chương 3: Góc với đường tròn

---------------------------------------------------

Chuyên đề Nhắc lại và bổ sung các khái niệm về hàm số - Toán 9

A. Lý thuyết

1. Khái niệm hàm số

• Nếu đại lượng y phụ thuộc vào một đại lượng x thay đổi sao cho mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số

• Hàm số có thể được cho bằng bảng hoặc bằng công thức, ...

Ví dụ 1.

+) y là hàm số của x được cho dưới dạng bảng:

x	− 1	0	1	2
y	3	0	− 3	− 6

+) y là hàm số của x được cho dưới dạng công thức: $y=\frac{1}{2}x$; y = x + 2; y = 5x.

• Hàm số thường được ký hiệu bởi những chữ f, g, h, ... chẳng hạn khi y là hàm số của biến số x, ta viết y = f(x) hoặc y = g(x), ….

• f(a) là giá trị của hàm số y = f(x) tại x = a. Khi hàm số y được cho bởi công thức y = f(x), muốn tính giá trị f(a) của hàm số tại x = a, ta thay x = a vào biểu thức f(x) rồi thực hiện các phép tính trong biểu thức.

Ví dụ 2. Ta có hàm số y = f(x) = 2x + 1.

Khi đó, f(2) = 2 . 2 + 1 = 5.

• Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là một hàm hằng.

Ví dụ 3. Ta có y = f(x) = 3.

Khi đó với giá trị nào của x thì y = 3.

Vậy y là hàm hằng.

2. Đồ thị của hàm số

Tập hợp các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ được gọi là đồ thị của hàm số y = f(x).

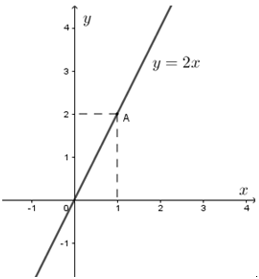
Ví dụ 4. Cho đồ thị của hàm số y = f(x) = 2x.

Các cặp giá trị tương ứng trên mặt phẳng tọa độ là O(0; 0); A(1; 2).

3. Hàm số đồng biến, nghịch biến

Cho hàm số y = f(x) xác định với mọi giá trị của x thuộc $ℝ$.

• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng cũng tăng lên thì hàm số y = f(x) được gọi là hàm số đồng biến trên $ℝ$ (gọi tắt là hàm số đồng biến).

• Nếu giá trị của biến x tăng lên mà giá trị của f(x) tương ứng giảm đi thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến).

Nói cách khác, cho hàm số y = f(x) xác định trên tập số thực R. Với $x_1,x_2\in ℝ$ ta có:

+ Nếu x₁ < x₂ mà f(x₁) < f(x₂) thì hàm số đồng biến.

+ Nếu x₁ < x₂ mà f(x₁) > f(x₂) thì hàm số nghịch biến.

Ví dụ 5. Cho hàm số y = x – 5, xác định với $\forall x\in ℝ$.

Ta có: x₁ < x₂ $\iff$ x₁ – 5 < x₂ – 5.

Hay f(x₁) < f(x₂) nên hàm số y = x – 5 đồng biến trên $ℝ$.