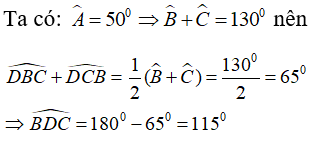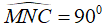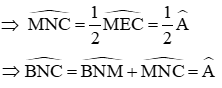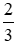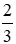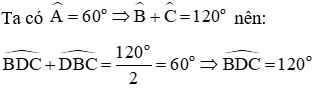Chuyên đề Cung chứa góc (2022) - Toán 9

Chuyên đề Cung chứa góc - Toán 9

A. Lý thuyết

1. Quỹ tích cung chứa góc

Với đoạn thẳng AB và góc α (0 < α < 180°) cho trước thì quỹ tích các điểm M thoả mãn $\widehat{AMB}=\alpha$ là hai cung chứa góc α dựng trên đoạn AB.

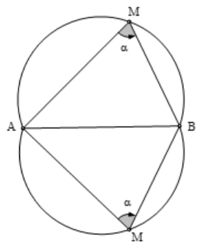
Lưu ý:

- Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB.

- Hai điểm A, B được coi là thuộc quỹ tích.

- Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.

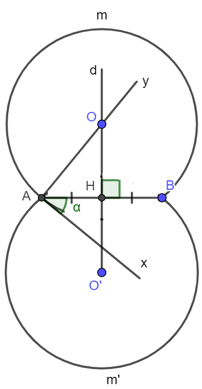
2. Cách vẽ cung chứa góc α

– Vẽ đường trung trực d của đoạn thẳng AB.

– Vẽ tia Ax sao cho $\widehat{BAx}=\alpha$.

– Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d.

– Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.

- $\stackrel{⏜}{AmB}$  được vẽ như trên là một cung chứa góc α.

Ta có hình vẽ:

3. Cách giải bài toán quỹ tích

Muốn chứng minh quỹ tích (tập hợp) các điểm M thoả mãn tính chất T là một hình H nào đó, ta phải chứng minh hai phần:

– Phần thuận: Mọi điểm có tính chất T đều thuộc hình H.

– Phần đảo: Mọi điểm thuộc hình H đều có tính chất T.

– Kết luận: Quỹ tích các điểm M có tính chất T là hình H.

Ví dụ. Cho góc xOy cố định và điểm A cố định nằm trên tia Ox. B là điểm chuyển động trên tia Oy. Tìm tập hợp trung điểm M của AB.

Lời giải:

 

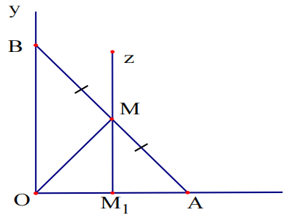
- Phần thuận:

+ Xét tam giác vuông OAB có OM = MA = MB

Nên ∆OAM cân tại M.

Mà OA cố định suy ra M nằm trên đường trung trực của đoạn thẳng OA.

- Phần đảo:

Lấy M bất kỳ thuộc tia M₁z, AM cắt Oy tại B.

Suy ra MO = MA $\Rightarrow \widehat{MAO}=\widehat{MOA}$.

Mặt khác $\widehat{OBM}=\widehat{BOM}$ (cùng phụ với góc $\widehat{MAO}=\widehat{MOA}$) suy ra MO = MB.

Suy ra MO = MA = MB.

Hay M là trung điểm của AB.

- Kết luận: Tập hợp các trung điểm M của AB là đường trung trực của đoạn OA.

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là

A. Đường tròn đường kính AB

B. Nửa đường tròn đường kính AB

C. Đường tròn đường kính AB/2

D. Đường tròn bán kính AB

Lời giải:

Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB

Chọn đáp án A

Câu 2: Với đoạn thẳng AB và góc α(0° < α < 180°) cho trước thì quỹ tích các điểm M thỏa mãn 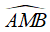 = α là

A. Hai cung chứa góc α dựng trên đoạn AB . Hai cung này không đối xứng nhau qua

B. Hai cung chứa góc α dựng trên đoạn AB và không lấy đoạn AB

C. Hai cung chứa góc α dựng trên đoạn AB . Hai cung này đối xứng nhau qua

D. Một cung chứa góc α dựng trên đoạn AB

Lời giải:

Với đoạn thẳng AB và góc α(0° < α < 180°) cho trước thì quỹ tích các điểm thỏa mãn 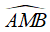 = α là hai cung chứa góc α dựng trên đoạn AB

Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB . Hai điểm A, B được coi là thuộc quỹ tích

Chọn đáp án C

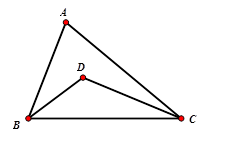
Câu 3: Cho tam giác ABC có BC cố định và góc A bằng 50° . Gọi D là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm D

A. Một cung chứa góc 115° dựng trên đoạn BC

B. Một cung chứa góc 115° dựng trên đoạn AC

C. Hai cung chứa góc 115° dựng trên đoạn AB

D. Hai cung chứa góc 115° dựng trên đoạn BC

Lời giải:

Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC

Chọn đáp án D

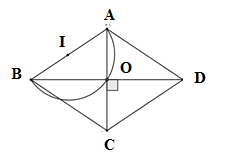
Câu 4: Cho các hình thoi ABCD có cạnh AB cố định . Tìm quỹ tích giao điểm của hai đường chéo của hình thoi đó .

A. Quỹ tích điểm O là 2 cung chứa góc 120° dựng trên AB

B. Quỹ tích điểm O là nửa đường tròn đường kính AB, trừ hai điểm A và B

C. Quỹ tích điểm O là 2 cung chứa góc 60° dựng trên AB

D. Quỹ tích điểm O là 2 cung chứa góc 30° dựng trên AB

Lời giải:

Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường

Suy ra AO ⊥ BO ⇒ 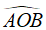 = 90°

Ta có 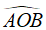 = 90° không đổi mà cố định

⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B

Chọn đáp án B

Câu 5: Cho tứ giác ABCD có 2 đường chéo vuông góc với nhau tại O.Biết 2 điểm A và B cố định, 2 điểm C và D di chuyển. Tìm quỹ tích điểm O

A. Đường tròn đường kính AB.

B. Đường tròn bán kính AB.

C. Đường tròn bán kính AB/2

D. Đường tròn đường kính 2AB

Lời giải:

Ta có: AC vuông góc BD tại O nên: 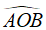 = 90°

Suy ra: quỹ tích điểm O là đường tròn đường kính A

Chọn đáp án A.

Câu 6: Cho đoạn thẳng BC cố định. Lấy điểm A bất kì sao cho tam giác ABC cân tại

A. Tìm quỹ tích điểm A?

A. Đường tròn tâm B bán kính BC.

B. Đường tròn tâm C bán kính BC.

C. Đường trung trực của đoạn thẳng BC.

D. Đường tròn đường kính BC.

Lời giải:

Do tam giác ABC cân tại A nên AB = AC

Suy ra, A thuộc đường trung trực của đoạn thẳng B

Chọn đáp án C.

Câu 7: Cho hai điểm B và C cố định, lấy điểm A bất kì sao cho tam giác ABC vuông tại Gọi M và N lần lượt là trung điểm BC và A Tìm quỹ tích điểm N .

A. Đường tròn đường kính MC

B. Đường tròn đường kính BC

C. Đường tròn đường kính BM.

D. Đáp án khác

Lời giải:

Xét tam giác ABC có M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB

Suy ra: MN// AB

Lại có: AB ⊥ AC ⇒ MN ⊥ AC

Suy ra: 

Vì B và C cố định nên trung điểm M của BC cũng cố định

Do đó, quỹ tích các điểm N là đường tròn đường kính MC.

Chọn đáp án A.

Câu 8: Cho hai điểm B và C cố định. Lấy A là điểm bất kì sao cho tam giác ABC cân tại

A. Gọi H là trực tâm của tam giác AB

C. Tìm quỹ tích điểm H

A. Đường tròn đường kính BC

B. Đường trung trực của đoạn thẳng BC

C. Đường tròn tâm B, bán kính BC

D. Đường tròn tâm C, bán kính BC

Lời giải:

Vì H là trực tâm của tam giác ABC nên AH ⊥ BC

Lại có tam giác ABC là tam giác cân tại A nên đường cao AH đồng thời là đường trung trực.

Suy ra: H nằm trên đường trung trực của đoạn thẳng BC.

Chọn đáp án B.

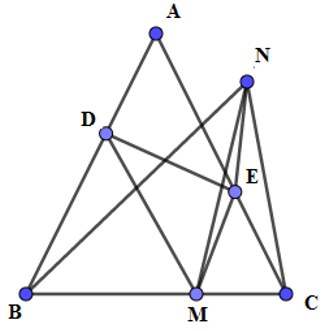
Câu 9: Cho tam giác ABC cân tại A, M là điểm trên cạnh đáy BC. Qua M kẻ các đường thẳng song song với hai cạnh bên cắt hai cạnh đó tại D và E. Gọi N là điểm đối xứng của M qua DE. Quỹ tích các điểm N là:

A. Quỹ tích các điểm N là cung chứa góc bằng 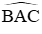 dựng trên đoạn BC

B. Quỹ tích các điểm N là cung chứa góc bằng 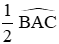 dựng trên đoạn BC

C. Quỹ tích các điểm N là cung chứa góc bằng 2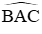 dựng trên đoạn BC

D. Quỹ tích các điểm N là cung chứa góc bằng 180^o − 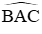 dựng trên đoạn BC

Lời giải:

(góc nội tiếp bằng nửa góc ở tâm cùng chắn cung BM)

Tương tự, E là tâm đường tròn ngoại tiếp tam giác CMN

Suy ra N nhìn đoạn BC dưới một góc bằng 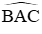 không đổi

Nên quỹ tích các điểm N là cung chứa góc bằng 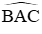 dựng trên đoạn BC

Đáp án cần chọn là: A

Câu 10: Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 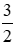 MB. Quỹ tích các điểm I là:

A. Quỹ tích điểm I là 2 cung chứa góc 45^o dựng trên AB

B. Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 2

C. Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 

D. Quỹ tích điểm I là 2 cung chứa góc 60^o dựng trên AB với tan a = 

Lời giải:

Tam giác AMB vuông tại M, ta có 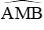 = 90^o. Mặt khác ta có

Mà A, B cố định ⇒ Quỹ tích điểm I là 2 cung chứa góc a^o dựng trên AB với tan a = 

Đáp án cần chọn là: D

II. Bài tập tự luận có lời giải

Câu 1: Từ điểm S nằm ở ngoài đường tròn (O) kẻ tiếp tuyến SA; SB với A, B là tiếp điểm và cát tuyến SCD với đường tròn. Gọi I là trung điểm của CD. Chứng minh 5 điểm A, I, O, B, S cùng thuộc một đường tròn.

Lời giải:

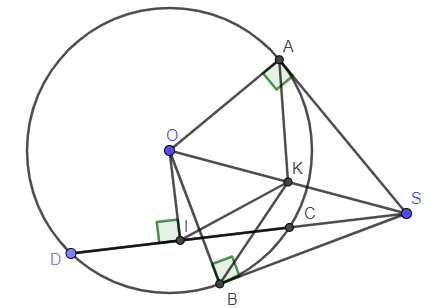
Vì SA là tiếp tuyến của đường tròn, A là tiếp điểm nên SA vuông góc với OA.

$\Rightarrow \widehat{SAO}=90°$

Vì SB là tiếp tuyến của đường tròn, B là tiếp điểm nên SB vuông góc với OB.

$\Rightarrow \widehat{SBO}=90°$

Vì I là trung điểm của CD nên OI vuông góc với CD (tính chất)

$\Rightarrow \widehat{SOI}=90°$

Gọi trung điểm của SO là K.

Tam giác OAS vuông tại A với K là trung điểm của SO

$\Rightarrow OK=KS=AK=\frac{1}{2}SO$ (định lí đường trung tuyến ứng với cạnh huyền)   (1)

Tam giác OBS vuông tại B với K là trung điểm của SO

$\Rightarrow OK=KS=BK=\frac{1}{2}SO$ (định lý đường trung tuyến ứng với cạnh huyền)   (2)

Tam giác OIS vuông tại I có K là trung điểm của SO

$\Rightarrow OK=KS=IK=\frac{1}{2}SO$ (định lí đường trung tuyến ứng với cạnh huyền)   (3)

Từ (1); (2); (3) $\Rightarrow OK=KS=IK=AK=BK=\frac{1}{2}SO$

Hay 5 điểm A, B, S, I, O cách đều điểm K.

Vậy 5 điểm A, B, S, I, O cùng nằm trên một đường tròn (K) bán kính KS.

Câu 2: Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo. Trên OA lấy điểm M sao cho OM = OB. Trên OB lấy N sao cho ON = OA. Chứng minh: 4 điểm D, M, N, C thuộc cùng một đường tròn.

Lời giải:

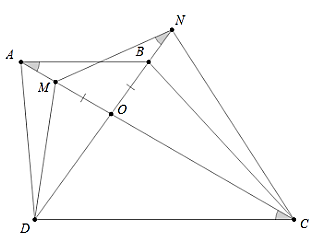
Xét tam giác OAB và tam giác OMN có:

$\widehat{AOB}$ chung

OA = ON

OB = OM

Do đó $\Delta AOB=\Delta NOM$ (c – g – c)

$\Rightarrow \widehat{BAO}=\widehat{MNO}$ (hai góc tương ứng)    (1)

Mặt khác, do ABCD là hình thang nên AB // CD (giả thuyết)

$\Rightarrow \widehat{BAO}=\widehat{DCO}$ (hai góc so le trong)    (2)

Từ (1) và (2) $\Rightarrow \widehat{MNO}=\widehat{DCO}$

Hai góc này cùng nhìn cạnh MD.

Do đó hai điểm N, C cùng nằm trên cung tròn dựng trên đoạn MD với góc $\widehat{DCO}$.

Câu 3: Dựng hình thang cân ABCD (AB // CD), biết CD = 3cm, AC = 4cm, $\widehat{D}=70°$.

Lời giải:

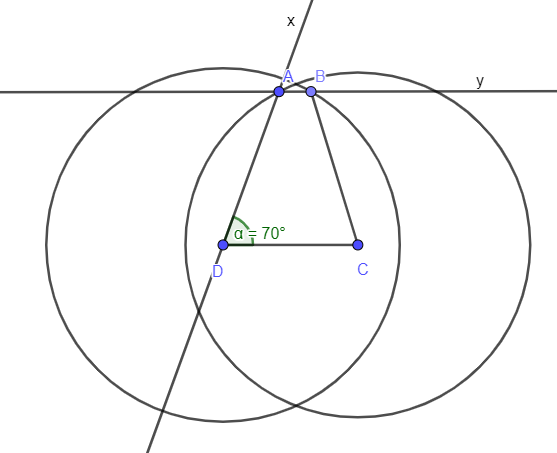
Cách dựng hình:

- Dựng đoạn CD = 3cm.

- Dựng góc $\widehat{CDx}=70°$.

- Trên nửa mặt phẳng bờ CD chứa tia Dx dựng đường tròn tâm C bán kính 4cm cắt Dx tại A.

- Dựng dây Ay song song với CD.

- Trên nửa mặt phẳng bờ CD chứa điểm A, dựng cung tròn tâm D bán kính 4cm cắt Ay tại B.

- Nối B với C ta được hình thang ABCD cần dựng.

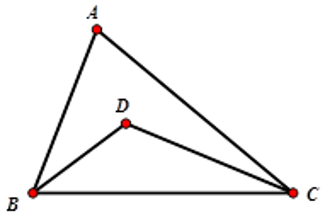
Câu 4: Cho tam giác ABC, BC cố định, $\widehat{A}=50°$. Gọi D là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm D.

Lời giải:

 

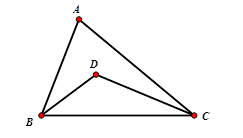
Xét tam giác ABC ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác)

$\Rightarrow \widehat{B}+\widehat{C}=180°-50°$

$\iff \widehat{B}+\widehat{C}=130°$

Lại có:

 D là giao điểm của ba đường phân giác trong của tam giác ABC nên BD là phân giác $\widehat{B}$.

$\Rightarrow \widehat{DBC}=\frac{1}{2}\widehat{B}$

D là giao điểm của ba đường phân giác trong của tam gác ABC nên CD là phân giác $\widehat{C}$.

$\Rightarrow \widehat{DCB}=\frac{1}{2}\widehat{C}$

Do đó:

$\widehat{DBC}+\widehat{DCB}=\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{C}$

$\iff \widehat{DBC}+\widehat{DCB}=\frac{1}{2}\left(\widehat{B}+\widehat{C}\right)$

$\iff \widehat{DBC}+\widehat{DCB}=\frac{1}{2}.130°$

$\iff \widehat{DBC}+\widehat{DCB}=65°$

Xét tam giác BCD có:

$\widehat{BDC}+\widehat{DBC}+\widehat{DCB}=180°$

$\iff \widehat{BDC}+65°=180°$

$\iff \widehat{BDC}=180°-65°$

$\iff \widehat{BDC}=115°$

Do BC cố định nên quỹ tích điểm D là hai cung chứa góc $115°$dựng trên đoạn BC.

Câu 5: Cho nửa đường tròn (O) đường kính AB. C là một điểm di động trên đường tròn. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại C. Tìm quỹ tích điểm D.

Lời giải:

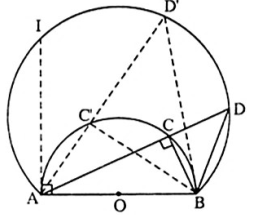
Phần thuận:

Ta có:

$\widehat{ACB}$ là góc nội tiếp chắn nửa đường tròn

$\Rightarrow \widehat{ACB}=90°$

Lại có:

$\widehat{DCB}$ (do tam giác BCD vuông cân tại C)

Do đó: $\widehat{ACB}+\widehat{DCB}=180°$

=> A, C, D thẳng hàng.

$\Rightarrow \widehat{ADB}=\widehat{CDB}=45°$ (do tam giác BCD vuông cân)

Vì AB cố định nên D nằm trên cung chứa góc $45°$dựng trên đoạn AB.

Dựng đường thẳng vuông góc với AB tại A, đường thẳng này giao với cung chứa góc $45°$dựng trên đoạn AB là I.

Nếu $C\equiv A\Rightarrow D\equiv I$

Phần đảo:

Lấy điểm D’ bất kỳ trên cung chứa góc $45°$ dựng trên đoạn Ab (D’ thuộc cung IB). Nối AD’ cắt nửa đường tròn (O) tại C’. Ta đi chứng minh tam giác BCD’ vuông cân tại C’

Ta có:

$\widehat{A{C}^{\text{'}}B}=90°$(góc nội tiếp chắn nửa đường tròn)

nên $\widehat{B{C}^{\text{'}}{D}^{\text{'}}}=90°$ (kề bù với góc $\widehat{A{C}^{\text{'}}B}$)

mà $\widehat{C^{\text{'}}{D}^{\text{'}}B}=45°$do đó tam giác BC’D’ vuông cân tại C’.

Vậy quỹ tích điểm D là cung BI của cung chứa góc $45°$dựng trên đoạn AB.

Câu 6: Cho một góc vuông xOy, trên tia Ox lấy điểm A cố định, B là điểm chuyển động trên tia Oy. Tìm tập hợp các điểm C sao cho DABC vuông cân tại C.

Lời giải:

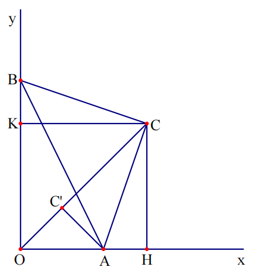
Do đó C thuộc tia phân giác Oz của góc vuông xOy.

- Phần đảo: Lấy điểm C bất kỳ thuộc tia C’z.

Vẽ đường thẳng vuông góc CA tại C cắt tia Oy tại B.

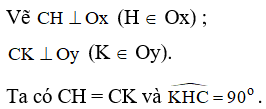
Xét ∆CAH vuông tại H và ∆CBK vuông tại K có:

CH = CK và $\widehat{CAH}=\widehat{CBK}$

Nên DCAH = DCBK (cạnh góc vuông – góc nhọn kề)

Suy ra CA = CB (hai cạnh tương ứng).

Do đó DABC vuông cân tại C.

- Kết luận: Tập hợp các điểm C là tia C’z của tia phân giác Oz của góc xOy.

Câu 7: Cho hình bình hành ABCD có cạnh AB cố định và cạnh CD chuyển động trên đường thẳng d song song với AB. Gọi I là trung điểm của CD. Tia AI cắt BC tại N. Tìm quỹ tích điểm N khi CD thay đổi trên đường thẳng d.

Lời giải:

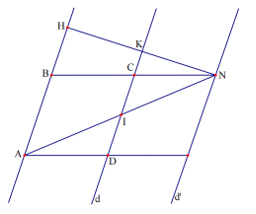
- Phần thuận:

Gọi khoảng cánh giữa đường thẳng AB và đường thẳng d là h không đổi.

Vì ABCD là hình bình hành nên BC // AD hay CN // AD.

Suy ra  $\widehat{IDA}=\widehat{ICN}$ (hai góc so le trong).

Xét ∆IAD và ∆INC có:

$\widehat{AID}=\widehat{CIN}$ (đối đỉnh)

ID = IC (vì I là trung điểm của CD)

$\widehat{IDA}=\widehat{ICN}$ (cmt)

Do đó DIAD = DINC (g.c.g)

Suy ra CN = AD (hai cạnh tương ứng)

Mà AD = BC (vì tứ giác ABCD là hình bình hành).

Do đó CN = AD = BC.

Kẻ $NH\perp AB$, NH cắt đường thẳng d tại K.

∆NBH có CB = CN và CK // BH nên suy ra KH = KN.

Từ đó ta được HN = 2KH = 2h không đổi.

Khi CD chuyển động trên đường thẳng d thì với mọi vị trí của CD, điểm N luôn cách đường thẳng AB một khoảng 2h không đổi.

Vậy điểm N thuộc đường thẳng d’ song song với đường thẳng AB và cách đường thẳng AB một khoảng 2h không đổi.

- Phần đảo: Lấy điểm N bất kì trên đường thẳng d’.

Đường thẳng AN cắt đường thẳng d tại I, đường thẳng NB cắt đường thẳng d tại C.

Lấy điểm D đối xứng với C qua điểm I.

Ta cần chứng minh tứ giác ABCD là hình bình hành và I là trung điểm của CD.

Thật vậy, Kẻ $NH\perp AB$, NH cắt đường thẳng d tại K.

Ta có K là trung điểm của HN.

Do đó trong ∆HNB thì C là trung điểm của NB. 9

Trong ∆NAB có C là trung điểm của BN và IC // AB.

Nên IC là đường trung bình.

Từ đó ta được $IC=\frac{1}{2}AB$.

Vì D đối xứng với C qua I nên ta được ID = IC =$\frac{1}{2}AB$.

Do đó AB = CD.

Mà AB // CD nên tứ giác ABCD là hình bình hành và I là trung điểm của CD.

- Kết luận: Vậy quỹ tích điểm N là đường thẳng d’ song song với đường thẳng AB và cách đường thẳng AB một khoảng 2h không đổi.

Câu 8: Cho đường tròn (O; R) cố định. Lấy B, C là hai điểm cố định trên đường tròn và A là một điểm tuỳ ý trên đường tròn. Gọi M là điểm đối xứng của điểm C qua trung điểm I của AB. Tìm quỹ tích các điểm M.

Lời giải:

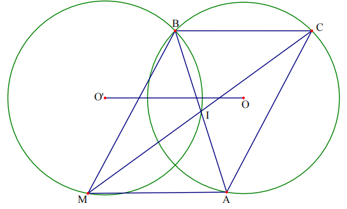
- Phần thuận:

Kẻ OO’// BC và OO’ = BC (O’ và B trên cùng một nửa mặt phẳng bờ AC).

Do đó ta được O’ cố định (vì O, B, C cố định và BC không đổi).

Xét tứ giác AMBC có:

IA = IB (vì I là trung điểm của AB)
IC = IM (vì điểm M đối xứng với B qua I)

Do đó tứ giác AMBC là hình bình hành.

Suy ra MA // BC và MA = BC

Mà OO’// BC và OO’ = BC

Do đó MA // OO’ và MA = OO’

Từ đó ta được tứ giác AMO’O là hình bình hành.

Nên suy ra O’M = OA = R không đổi và O’ cố định.

Do đó khi A di động thì M di động theo nhưng M luôn cách O’ cố định một khoảng không đổi là O’M = OA = R.

Vậy M thuộc đường tròn tâm O’ bán kính OA = R.

- Phần đảo: Trên đường tròn (O’; R) lấy điểm M bất kỳ. Nối MB.

Qua C kẻ đường thẳng song song với BM cắt đường tròn (O) ở điểm thứ hai A. Ta dễ dàng chứng minh được M đối xứng với C qua trung điểm I của AB.

- Kết luận: Do đó khi A di động thì M di động theo nhưng M luôn cách O’ cố định một khoảng không đổi là O’M = OA= R.

Vậy quỹ tích điểm M là đường tròn tâm O’ bán kính OA = R.

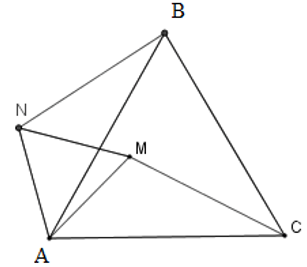
Câu 9: Cho tam giác đều ABC. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho MB² = MA² + MC²

Lời giải:

Vẽ tam giác AMN đều (N khác phía C đối với AM)

Xét ∆BNA và ∆AMC có:

AN = AM (vì tam giác AMN đều)

BA = BC (Vì tam giác ABC đều)

Suy ra ∆ANB = ∆AMC (c.g.c) nên ta có NB = MC

Ta có MB² = MA² + MC² = MN² + NB² nên 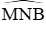 = 90^o

B, C cố định ⇒ Quỹ tích điểm M là hai cung chứa góc 150^o dựng trên AC, trừ hai điểm A và C.

Câu 10: Cho tam giác ABC có BC cố định và góc A bằng 60^o. Gọi D là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm D

Lời giải:

Quỹ tích của điểm D là hai cung chứa góc 120^o dựng trên đoạn BC

III. Bài tập vận dụng

Câu 1: Cho tam giác ABC vuông tại A, BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.

Câu 2: Dựng tam giác vuông ABC với cạnh huyền BC = 4,5cm, AB = 2cm.

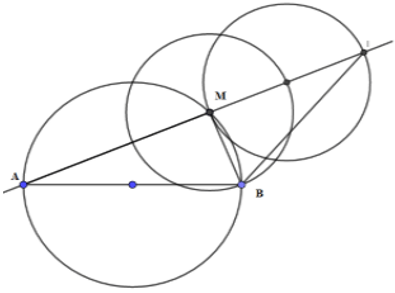
Câu 3: Cho nửa đường tròn đường kính AB. Gọi M là điểm chính giữa cung AB. Trên cung AM lấy điểm N. Trên tia đối của tia Am lấy điểm D sao cho MD = MB, trên tia đố tia NB lấy điểm E sao cho NA = NE, trên tia đối của tia MB lấy điểm C sao cho MC = MA. Chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn.

Câu 4: Dựng một cung chứa góc $55°$trên đoạn AB = 3cm

Câu 5: Cho I và O lần lượt là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC với $\widehat{A}=60°$. Gọi H là trực tâm của tam giác ABC. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.

Câu 6: Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích điểm M khi E di động trên BC.

Câu 7: Cho cung AB cố định tạo bởi các bán kính OA, OB vuông góc với nhau, điểm I chuyển động trên cung AB. Trên tia OI lấy điểm M sao cho OM bằng tổng các khoảng cách từ điểm I đến OA, OB, Tìm quỹ tích các điểm M.

Câu 8: Cho tam giác ABC vuông tại A, phân giác BF. Từ điểm I nằm giữa B và F vẽ đường thẳng song song với AC cắt AB, BC lần lượt tại M và N. Vẽ đường tròn ngoại tiếp tam giác BIN cắt Ai tại D. Hai đường thẳng DN và BF cắt nhau tại E. Chứng minh:

a) Bốn điểm A, B, D, E cùng thuộc một đường tròn.

b) Năm điển A, B, C, D, E cùng thuộc một đường tròn. Từ đó suy ra BE vuông góc với CE.

Câu 9: Từ điểm M nằm bên ngoài đường tròn (O), kẻ cát tuyến MAB đi qua O và các tiếp tuyến MC, MD. Gọi K là giao điểm của AC và BD. Chứng minh 4 điểm B, C, M, K thuộc cùng một đường tròn.

Câu 10: Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB.

a) Chứng minh $\widehat{AIB}$ không đổi.

b) Tìm tập hợp tất cả các điểm I nói trên.

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Tứ giác nội tiếp

Chuyên đề Đường tròn ngoại tiếp. Đường tròn nội tiếp

Chuyên đề Độ dài đường tròn, cung tròn

Chuyên đề Diện tích hình tròn, hình quạt tròn

Chuyên đề Ôn tập chương III

•