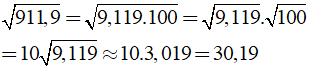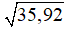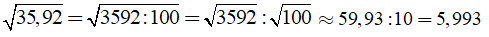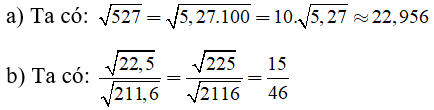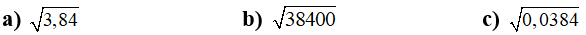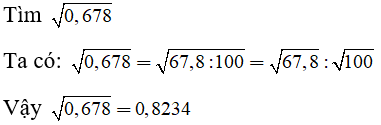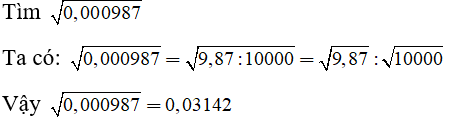Chuyên đề Bảng căn bậc hai (2022) - Toán 9

Chuyên đề Bảng căn bậc hai - Toán 9

A. Lý thuyết

1. Giới thiệu bảng căn bậc hai

+ Bảng được chia thành các hàng và các cột.

+ Căn bậc hai của các số được viết bởi không qua ba chữ số từ 1,00 đến 99,9 được ghi sẵn trong bảng ở các cột từ cột 0 đến cột 9.

+ Tiếp đó là chín cột hiệu chính được dùng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn chữ số từ 1,000 đến 99,99.

+ Bảng căn bậc hai.

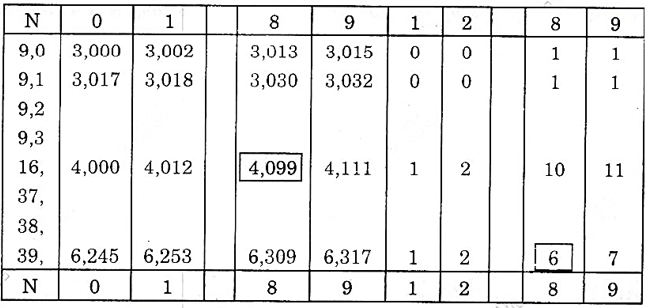
2. Cách dùng bảng

a) Tìm căn bậc hai của số lớn hơn 1 và nhỏ hơn 100

Ví dụ 1. Tìm $\sqrt{\mathrm{1,68}}$.

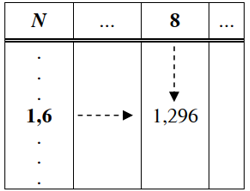
Tại giao của hàng 1,6 và cột 8, ta thấy số 1,296.

Vậy $\sqrt{\mathrm{1,68}}\approx \mathrm{1,269}$.

Ví dụ 2. Tìm $\sqrt{\mathrm{39,18}}$.

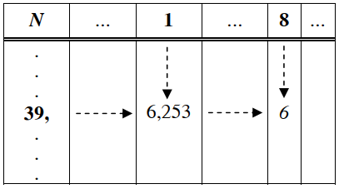
Tại giao của hàng 39 và cột 1, ta thấy số 6,253.

Ta có: $\sqrt{\mathrm{39,1}}\approx \mathrm{6,253}$.

Tại giao của hàng 39 và cột 8 hiệu chính, ta thấy số 6.

Ta dùng số 6 này để hiệu chính chữ số cuối ở số 6,253 như sau:

6,253 + 0,006 = 6,259.

Vậy $\sqrt{\mathrm{39,18}}\approx \mathrm{6,259}$.

b) Tìm căn bậc hai của số lớn hơn 100

Ví dụ 3. Tìm $\sqrt{998}$.

Ta có:

$$\begin{gathered} \sqrt{998}=\sqrt{\mathrm{9,88}.100} \\ =10.\sqrt{\mathrm{9,88}} \end{gathered}$$

≈ 10 . 3,143 = 31,43.

Vậy $\sqrt{998}\approx \mathrm{31,43}$.

c) Tìm căn bậc hai của số không âm và nhỏ hơn 1

Chú ý. Để thực hành nhanh, khi tìm căn bậc hai của số không âm lớn hơn 100 hoặc nhỏ hơn 1, ta dùng hướng dẫn của bảng: “Khi dời dấu phẩy trong số N đi 2, 4, 6, …chữ số thì dời dấu phẩy trong số N đi 1, 2, 3, …chữ số”.

Ví dụ 4.Tìm $\sqrt{\mathrm{0,678}}$.

Ta có

$$\begin{gathered} \sqrt{\mathrm{0,678}}=\sqrt{\mathrm{67,8}:100} \\ =\sqrt{\mathrm{67,8}}:\sqrt{100} \end{gathered}$$

 

≈ 8,234 : 10 = 0,8234.

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Khẳng định nào sau đây đúng

Lời giải:

Chọn đáp án C.

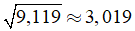
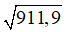
Câu 2: Biết  . Giá trị  gần với giá trị nào nhất

A. 0,319

B. 30,19

C. 301,9

D. 31,9

Lời giải:

Ta có:

Chọn đáp án B.

Câu 3: Biết 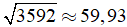 . Tính 

A. 0,5993

B. 599,3

C. 59,93

D. 5,993

Lời giải:

Ta có:

Chọn đáp án D.

Câu 4: Rút gọn biểu thức $\frac{3m}{8n}\sqrt{\frac{64n^2}{9m^2}}$ với m > 0; n < 0, ta được?

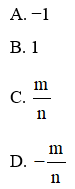
Đáp án: A

Giải thích:

Câu 5: Rút gọn biểu thức $E=\frac{a-b}{2\sqrt{a}}\sqrt{\frac{ab}{{(a-b)}^2}}$ với 0 < a < b, ta được:

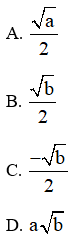
Đáp án: C

Giải thích:

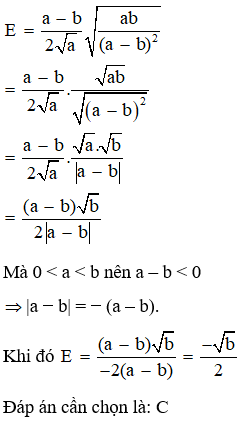
Câu 6: Rút gọn biểu thức $\frac{\sqrt{x^3+2x^2}}{\sqrt{x+2}}$ với x > 0, ta được?

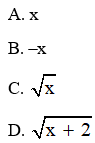
Đáp án: A

Giải thích:

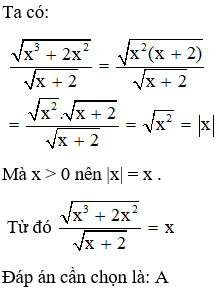
Câu 7: Với $a\ge 0,b\ge 0,a\ne b,$ rút gọn biểu thức $\frac{a-b}{\sqrt{a}-\sqrt{b}}-\frac{\sqrt{a^3}+\sqrt{b^3}}{a-b}$ta được?

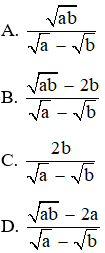
Lời giải

Đáp án: B

Giải thích:

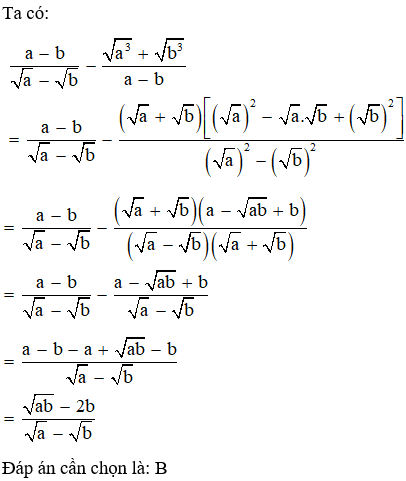
Câu 8: Với $a\ge 0,b\ge 0,2a\ne 3b,$ rút gọn biểu thức $\frac{2a+3b}{\sqrt{2a}+\sqrt{3b}}+\frac{\sqrt{8a^3}-\sqrt{27b^3}}{3b-2a}$ta được?

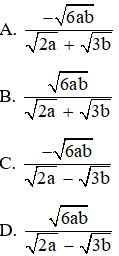
Đáp án: A

Giải thích:

Câu 9: Với x > 5, cho biểu thức $A=\frac{\sqrt{x^2-5x}}{\sqrt{x-5}}$và B = x.

Có bao nhiêu giá trị của x để A = B?

A. 1                            

B. 2                            

C. 0                            

D. Vô số

Đáp án: C

Giải thích:

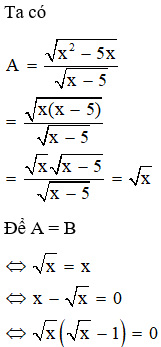
Câu 10: Rút gọn biểu thức $4a^4{b}^2.\sqrt{\frac{9}{a^8{b}^4}}$ với $ab\ne 0$, ta được?

Đáp án: B

Giải thích:

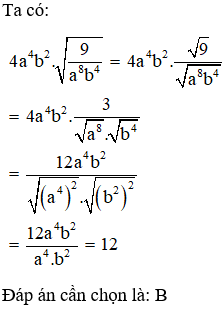
II. Bài tập tự luận có lời giải

Câu 1: Tìm 

Lời giải:

Tại giao của hàng 1,4 và cột 1 ta thấy số 1,187

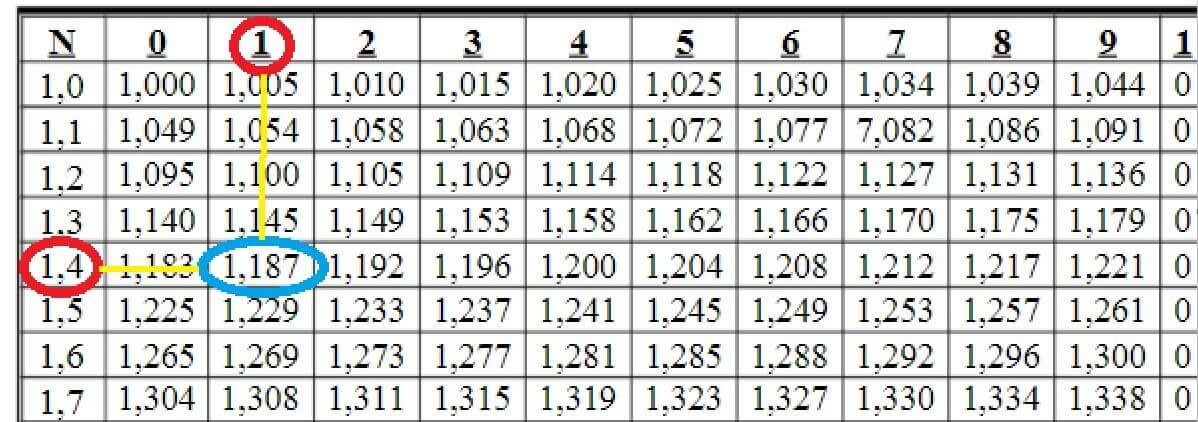
Vậy 

(các bạn học sinh có thể kiểm tra kết quả lại bằng máy tính)

Câu 2: Tìm 

Lời giải:

Tại giao của hàng 2,3 và cột 5 ta thấy số 1,533. Ta có 

Tiếp đến, tại giao của hàng 2,3 và cột 4 hiệu chính ta thấy số 1, số 1 này để hiệu chính chữ số cuối ở số . Đó là: 1,533 + 0,001 = 1,534

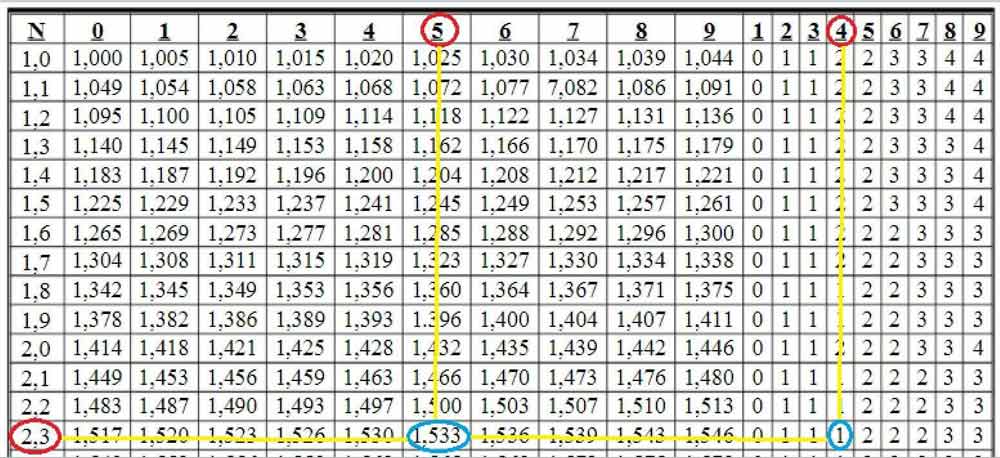
Vậy 

(các bạn học sinh có thể kiểm tra kết quả lại bằng máy tính)

Câu 3: Tìm 

Lời giải:

Có 

Sử dụng bảng căn bậc hai ta được 

Vậy 

Câu 4: Tìm 

Lời giải:

Có 

Sử dụng bảng căn bậc hai ta được 

Vậy 

Câu 4: Dùng bảng số để tìm căn bậc hai số học của 115 và 9691 rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả.

Lời giải:

* Căn bậc hai của 115:

- Dùng bảng căn bậc hai:

Ta có:

$$\begin{gathered} \sqrt{115}=\sqrt{100}.\sqrt{\mathrm{1,15}} \\ =10.\sqrt{\mathrm{1,15}} \end{gathered}$$

Tại hàng 1,5 cột 5: $10.\sqrt{\mathrm{1,15}}\approx 10.\mathrm{1,072}=\mathrm{10,72}$.

- Dùng máy tính: $\sqrt{115}\approx \mathrm{10,72380529}$.

Ta thấy sử dụng máy tính cho kết quả chính xác hơn.

* Căn bậc hai của 9691:

- Dùng bảng căn bậc hai:

Ta có:

$$\begin{gathered} \sqrt{9691}=\sqrt{100}.\sqrt{\mathrm{96,91}} \\ =10.\sqrt{\mathrm{96,91}} \end{gathered}$$

+ Tại hàng 96 cột 9: $\sqrt{\mathrm{96,91}}\approx \mathrm{9,844}$.

+ Tại giao của hàng 96 và cột 1 hiệu chính ta thấy số 0.

Nên $\sqrt{\mathrm{96,91}}\approx \mathrm{9,844}$suy ra $\sqrt{9691}=10.\mathrm{9,844}=\mathrm{98,44}$.

- Dùng máy tính: $\sqrt{115}\approx \mathrm{98,44287684}$.

Ta thấy sử dụng máy tính cho kết quả chính xác hơn.

Câu 5: Biết $\sqrt{\mathrm{9,119}}\approx \mathrm{3,019}$. Hãy tính:

$\sqrt{91190}$; $\sqrt{\mathrm{0,09119}}$.

Lời giải:

$$\begin{gathered} \sqrt{91190}=\sqrt{9119.10000} \\ =\sqrt{91190}.\sqrt{10000} \end{gathered}$$

≈ 3,019 . 100 = 301,9;

$$\begin{gathered} \sqrt{\mathrm{0,09119}}=\sqrt{9119:100} \\ =\sqrt{9119}:\sqrt{100} \end{gathered}$$

≈ 3,019 : 10 = 0,3019.

Câu 6: Dùng bảng căn bậc hai để tính

Lời giải:

Câu 7: Biết 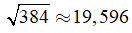 . Tính

Lời giải:

Câu 8:

Câu 9:

Câu 10: Kiểm tra kết quả bằng máy tính bỏ túi.

Lời giải:

a) Ta có: x² = 15

⇒ x₁ = $\sqrt{15}$ = 3,872983346 ≈ 3,873

x₂ = -$\sqrt{15}$ = -3,872983346 ≈ -3,873

b) Ta có: $x^2$ = 22,8

$\Rightarrow x_1=\sqrt{22,8}=4,\mathrm{774934555...}\approx 4,7749$

$x_2=-\sqrt{22,8}=-4,\mathrm{774934555...}\approx -4,7749$

c) Ta có: $x^2$ = 351

$\Rightarrow x_1=\sqrt{351}=18,\mathrm{734994...}\approx 18,735$

$x_2=-\sqrt{351}=-18,\mathrm{734994...}\approx -18,735$

d) Ta có: $x^2=0,46$

$\Rightarrow x_1=\sqrt{0,46}=0,\mathrm{6782329980...}\approx 0,6782$

$x_2=-\sqrt{0,46}=-0,\mathrm{6782329980...}\approx -0,6782$

III. Bài tập vận dụng

Câu 1: Dùng bảng căn bậc hai để tính

Câu 2: Biết 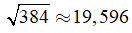 . Tính

Câu 3: Sử dụng bảng căn bậc hai tìm các bậc hai số học của mỗi số dưới đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

2,75

18,34

73,54

45,45

Câu 4: Sử dụng bảng căn bậc hai tìm các bậc hai số học của mỗi số dưới đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

657

4380

258

1920

Câu 5: Sử dụng bảng căn bậc hai tìm các bậc hai số học của mỗi số dưới đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả:

0,0245

0,355

0,000528

0,3816

Câu 6: Dùng bảng căn bậc hai để tìm giá trị gần đúng của nghiệm mỗi phương trình sau:

a,

b,

Câu 7: Biết , và . Tính:

Câu 8:

Dùng bảng căn bậc hai để tính giá trị gần đúng mỗi nghiệm của phương trình:

a)  = 2468                        b) 5 – 6810 = 0.

Câu 9:

Độ dài hai cạnh góc vuông của một tam giác vuông là 6,5 cm và 4,3 cm. Dùng bảng căn bậc hai để tính giá trị gần đúng độ dài cạnh huyền của tam giác vuông đó.

Câu 10:

Đường chéo của một hình vuông dài hơn cạnh của hình vuông 4,562 cm. Dùng bảng căn bậc hai để tính giá trị gần đúng độ dài cạnh hình vuông.

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Biến đổi đơn giản biểu thức chứa căn bậc hai

Chuyên đề Rút gọn biểu thức chứa căn thức bậc hai

Chuyên đề Căn bậc ba

Chuyên đề Ôn tập chương 1

Chuyên đề Nhắc lại và bổ sung các khái niệm về hàm số