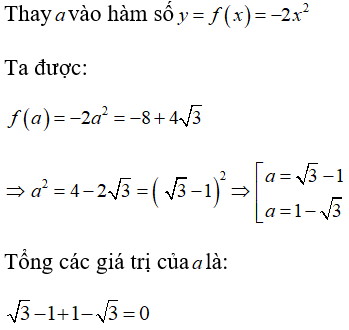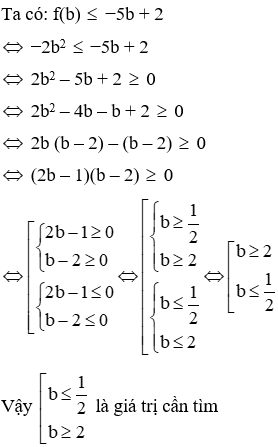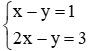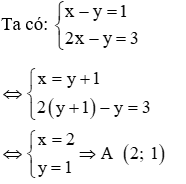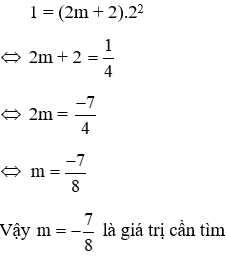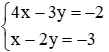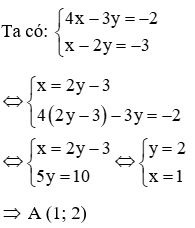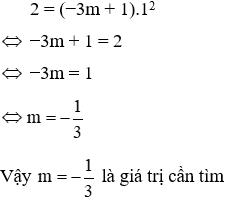Chuyên đề Hàm số y = ax^2 (a khác 0) (2022) - Toán 9
Với Chuyên đề Hàm số y = ax^2 (a khác 0) (2022) - Toán 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Hàm số y = ax^2 (a khác 0) - Toán 9
A. Lý thuyết
1. Tập xác định
Cho hàm số
Tập xác định của hàm số là R.
Ví dụ 1: là những hàm số có dạng .
2. Tính chất
Cho hàm số
+ Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Ví dụ 2:
a) Hàm số y = có a = 3 > 0 nên hàm số đồng biến khi x > 0 và nghịch biến khi x < 0.
b) Hàm số y = có a = -1 < 0 nên hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
3. Nhận xét
+ Nếu a > 0 thì y > 0 với mọi x ≠ 0; y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số y = 0.
+ Nếu a < 0 thì y < 0 với mọi x ≠ 0; y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0.
B. Bài tập
I. Bài tập trắc nghiệm
Câu 1: Cho hàm số y = ax2 với . Kết luận nào sau đây là đúng:
A. Hàm số nghịch biến khi a > 0 và x > 0
B. Hàm số nghịch biến khi a < 0 và x < 0
C. Hàm số nghịch biến khi a > 0 và x < 0
D. Hàm số nghịch biến khi a > 0 và x = 0
Cho hàm số y = ax2 (a ≠ 0)
• Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
• Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Chọn đáp án C.
Câu 2: Kết luận nào sau đây sai khi nói về đồ thị hàm số y = ax2 với a ≠ 0
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm cao nhất của đồ thị
C. Với a < 0 đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị
D. Với a > 0 đồ thị nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị
Đồ thị hàm số y = ax2 (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol).
• Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị
• Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị
Chọn đáp án B.
Câu 3: Giá trị của hàm số y = f(x) = -7x2 tại x0 = -2 là:
A. 28
B. 12
C. 21
D. -28
Thay x0 = -2 vào hàm số y = f(x) = -7x2 ta được: f(-2) = -7.(-2)2 = -28
Chọn đáp án D.
Câu 4: Cho hàm số y = f(x) = (-2m + 1)x2 . Tính giá trị của m để đồ thị đi qua điểm A(-2; 4)
A. m = 0
B. m = 1
C. m = 2
D. m = -2
Thay tọa độ điểm A(-2; 4) vào hàm số y = f(x) = (-2m + 1)x2 ta được:
(-2m + 1).(-2)2 = 4 ⇔ -2m + 1 = 1 ⇔ m = 0
Vậy m = 0 là giá trị cần tìm.
Chọn đáp án A.
Câu 5: Cho hàm số y = f(x) = -2x2. Tổng các giá trị a của thỏa mãn f(a) = -8 + 4√3 là:
A. 1
B. 0
C. 10
D. -10
Chọn đáp án B.
Câu 6: Cho hàm số y = (m + 1)x2 + 2. Tìm m biết rằng với x = 1 thì y = 5.
A. m = 2
B. m = -2
C. m = - 3
D.m = 3
Thay x = 1 và y = 5 vào y = (m + 1)x2 + 2 ta được:
5 = (m +1).12 + 2
⇔ m + 1 + 2 = 5 ⇔ m = 2
Chọn đáp án A.
Câu 7: Cho hàm số y= 2x2 . Tìm x khi y = 32 ?
A. x = 4
B. x = -4
C. x = 8 và x = -8
D. Đáp án khác
Thay y = 32 vào y = 2x2 ta được:
32 = 2.x2 ⇔ x2 = 16 ⇔ x = ±4
Chọn đáp án D.
Câu 8: Diện tích hình tròn bán kính R được cho bởi công thức: S = π.R2 .
Hỏi nếu bán kính tăng lên 6 lần thì diện tích tăng hay giảm bao nhiêu lần?
A. Tăng 6 lần
B. Tăng 12 lần
C. Tăng 36 lần
D. Giảm 6 lần
Diện tích hình tròn ban đầu là: S = π.R2
Khi tăng bán kính lên 6 lần thì bán kính mới là R’ = 6R.
Diện tích hình tròn mới là: S = π.R'2 = π.(6R)2 = 36πR2 = 36.S
Do đó, diện tích hình tròn mới tăng lên 36 lần.
Chọn đáp án C.
Câu 9: Cho các hàm số y = 2x2 và y = -3x2. Hỏi hàm số nào đồng biến khi x > 0.
A. y = 2x2
B. y = -3x2
C. Không có hàm số nào
D.Cả hai
Xét hàm số y = ax2 (a ≠ 0)
* Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
* Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Do đó,chỉ có hàm số y = 2x2 đồng biến khi x> 0.
Chọn đáp án A.
Câu 10: Cho các hàm số:
(1): y = 3x2 (2): y = - 4 x2 (3) y = 3x (4): y = - 4x .
Hỏi có bao nhiều hàm số đồng biến với x < 0?
A. 1
B.2
C. 3
D. 4
* Hàm số bậc nhất y = ax + b đồng biến khi a > 0 và hàm số này nghịch biến khi a < 0 .
Do đó, hàm số y = 3x đồng biến trên R nên cũng đồng biến khi x < 0 .
Hàm số y = -4x nghịch biến trên R.
* Xét hàm số y = ax2 (a ≠ 0)
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Trong hai hàm số y = 3x2 và y = -4x2 chỉ có hàm số y = -4x2 đồng biến khi x < 0
Vậy trong các hàm số đã cho chỉ có hàm số y = 3x và y = -4x2 đồng biến x < 0.
Chọn đáp án B.
II. Bài tập tự luận có lời giải
Câu 1: Cho hàm số y = f(x) = −2x2. Tìm b biết f(b) ≤ −5b + 2
Câu 2: Cho hàm số y = (2m + 2) x2. Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x: y) là nghiệm của hệ phương trình: 
Thay x = 2; y = 1 vào hàm số y = (2m + 2) x2 ta được:
Câu 3: Cho hàm số y = (−3m + 1)x2. Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x; y) là nghiệm của hệ phương trình 
Thay x = 1; y = 2 vào hàm số y = (−3m + 1)x2 ta được:
Câu 4: Cho hàm số y = (5m + 2)x2 với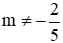 
. Tìm m để hàm số nghịch biến với mọi x > 0
Để hàm số nghịch biến với mọi x > 0 thì a < 0 nên 5m + 2 < 0 ⇔ 
Vậy 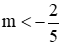thỏa mãn điều kiện đề bài
Câu 5: Cho hàm số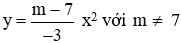 
. Tìm m để hàm số nghịch biến với mọi x < 0.
Để hàm số nghịch biến với mọi x < 0 thì a > 0 nên
Vậy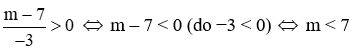 
thỏa mãn điều kiện đề bài
Vậy m < 7 thỏa mãn điều kiện đề bài
Câu 6: Một vật rơi ở độ cao so với mặt đất là 100m. Quãng đường chuyển động là s (mét) của vật rơi phụ thuộc vào thời gian là t (giây) bởi công thức: s = 4t2. Hỏi sau bao lâu vật này tiếp đất ?
Lời giải:
Thời gian để vật chạm đất là:
Vậy sau 5 (s) thì vật chạm đất.
Câu 7: Cho hai hàm số và . Tính các giá trị tương ứng của y rồi điền vào bảng sau:
Lời giải
Câu 8: Một vật rơi tự do từ độ cao so với mặt đất là 400m. Quãng đường chuyển động của vật rơi phụ thuộc vào thời gian bởi công thức s = 4t2 (quãng đường s(m), thời gian là t(s)). Hỏi sau bao lâu, vật này chạm đất?
Lời giải:
Ta có công thức tính quãng đường chuyển động là:
Theo giả thiết ta có: s = 400(m)
Khi đó ta có:
Vậy sau 10s thì vật này rơi chạm đất.
Câu 9: Cho hai hàm số y = 2x2 và y = -2x2. Với từng giá trị của x dưới đây hãy tính giá trị của y tương ứng và nhận xét ?
Lời giải:
| x | 0 | 1 | 3 | 4 |
| y = 2x2 | 0 | 2 | 18 | 32 |
| y = -2x2 | 0 | -2 | -18 | -32 |
Câu 10: Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.
a) Biểu diễn diện tích toàn phần S (tức là tổng diện tích của sáu mặt) của hình lập phương qua x.
b) Tính các giá trị của S ứng với các giá trị của x cho trong bảng dưới đây rồi điền vào các ô trống.
|
x |
|
|
1 |
|
2 |
3 |
|
S |
c) Nhận xét sự tăng, giảm của S khi x tăng.
d) Khi S giảm 16 lần thì cạnh x tăng hay giảm bao nhiêu lần ?
e) Tính cạnh của hình lập phương khi S = cm2, S = 5cm2.
Lời giải:
a) Diện tích của một mặt hình lập phương là x2.
Hình lập phương có 6 mặt nên có diện tích toàn phần 6x2.
b) Giá trị của S và x được thể hiện trong bảng sau:
|
x |
|
|
1 |
|
2 |
3 |
|
S |
|
|
6 |
|
24 |
54 |
c) Khi giá trị của x tăng thì giá trị của S tăng.
d) Gọi S’ là giá trị của S khi giảm đi 16 lần, x’ là cạnh hình lập phương khi S giảm đi 16 lần.
Ta có: (1)
S’ = (2)
Từ (1) và (2)
Vậy khi S giảm đi 16 lần thì cạnh hình vuông giảm đi 4 lần.
e) Khi ta có:
Vì x > 0 nên chọn giá trị x =
Vậy cạnh hình vuông là (cm).
Khi S = 5 ta có:
Vì x > 0 nên chọn giá trị x =
Vậy cạnh hình vuông là
III. Bài tập vận dụng
Câu 1: Tìm bán kính của đường tròn khi diện tích hình tròn bằng 16π2 (cm)
Câu 2: Một vật rơi tự do từ độ cao so với mặt đất là 400m. Quãng đường chuyển động của vật rơi phụ thuộc vào thời gian bởi công thức s = 4t2 ( quãng đường s(m) , thời gian là t(s) ) . Hỏi sau bao lâu, vật này chạm đất?
Câu 3: Cho hàm số y = 3x2.
a) Lập bảng tính các giá trị của y ứng với các giá trị của x lần lượt bằng : –2 ; –1 ; ; 0 ; ; 1 ; 2
b) Trên mặt phẳng tọa độ xác định các điểm mà hoành độ là giá trị của x còn tung độ là giá trị tương ứng của y đã tìm ở câu a.
Chẳng hạn, điểm A
Câu 4: Cho hàm số y = f(x) = –1,5x2
a) Hãy tính f(1), f(2), f(3) rồi sắp xếp các giá trị này theo thứ tự từ lớn đến bé.
b) Hãy tính f(–3), f(–2), f(–1) rồi sắp xếp các giá trị này theo thứ tự từ bé đến lớn.
c) Phát biểu nhận xét của em về sự đồng biến hay nghịch biến của hàm số này khi x > 0 ; khi x < 0
Câu 5: Điểm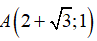 
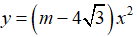
thuộc đồ thị hàm số 
(với m là tham số, m ≠ 
). Giá trị m là:
Câu 6: Một bể nước hình hộp chữ nhật có đáy hình vuông cạnh bằng x mét. Chiều cao của bể bằng 2m. Kí hiệu V(x) là thể tích của bể.
a) Tính thể tích V(x) theo x.
b) Giả sử chiều cao của bể không đổi, hãy tính V(1), V(2), V(3). Nhận xét khi x tăng lên 2 lần, 3 lần thì thể tích tương ứng của bể tăng lên mấy lần?
Câu 7: Biết rằng nhiệt lượng tỏa ra trên dây dẫn được tính bởi công thức: Q = 0,24RI2t. Trong đó Q là nhiệt lượng tính bằng calo, R là điện trở tính bằng ôm ( Ω), I là cường độ dòng điện tính bằng ampe (A), t là thời gian tính bằng giây (s). Dòng điện chạy qua một dây dẫn có điện trở R = 10 Ω trong thời gian 1 giây.
a) Hãy điền các số thích hợp vào bảng sau :
|
I (A) |
1 |
2 |
3 |
4 |
|
Q (calo) |
b) Hỏi cường độ dòng điện là bao nhiêu thì nhiệt lượng tỏa ta ra bằng 60 calo?
Câu 8: Đường thẳng y = x + 2 cắt đồ thị của hàm số y = (m - 1)x2 (với m là tham số, m ≠ 1) tại điểm có hoành độ bằng 2. Tính giá trị của tham số m
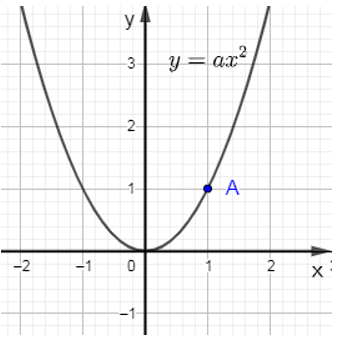
Câu 9: Cho hàm số y = ax2 (a ≠ 0) có đồ thị như hình vẽ sau đây:
Tính giá trị của a
Câu 10: Parabol (P): y = ax2 (a ≠ 0) đi qua điểm (2; 4) và tiếp xúc với đồ thị (d) của hàm số y = 2(m - 1)x + 1 - m. Xác định tọa độ tiếp điểm
Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:
Chuyên đề Đồ thị của hàm số y = ax^2 (a khác 0)
Chuyên đề Phương trình bậc hai một ẩn
Chuyên đề Công thức nghiệm của phương trình bậc hai
Chuyên đề Công thức nghiệm thu gọn
Chuyên đề Hệ thức Vi – ét và ứng dụng
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9