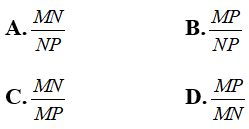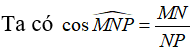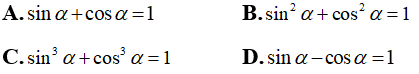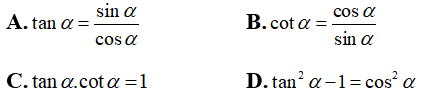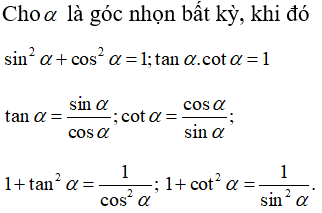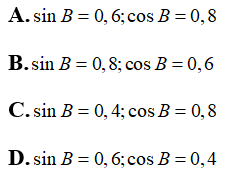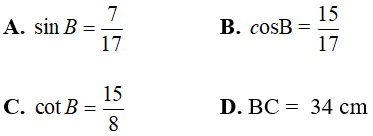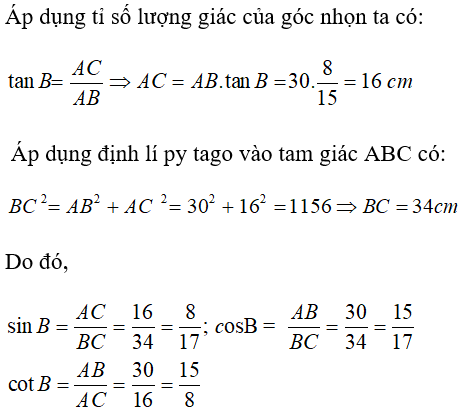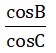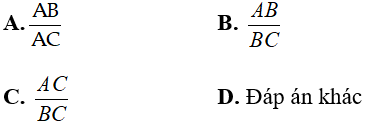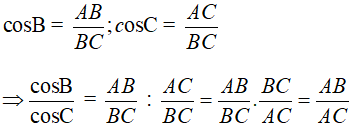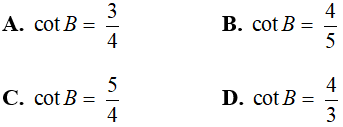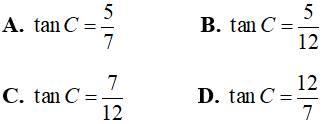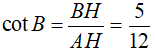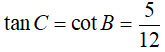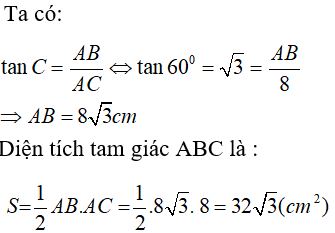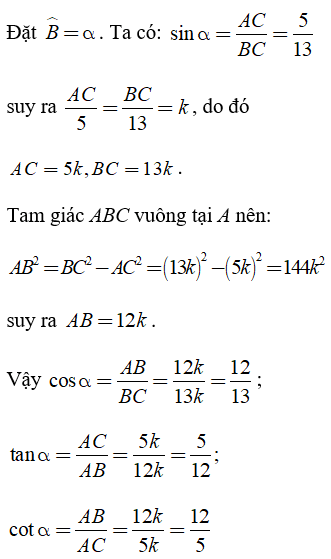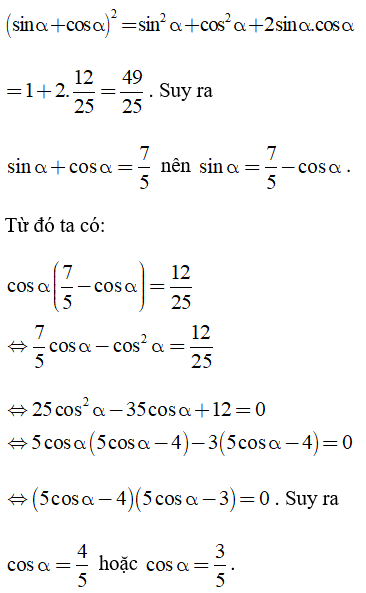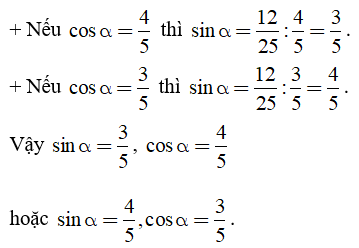Chuyên đề Tỉ số lượng giác của góc nhọn (2022) - Toán 9
Với Chuyên đề Tỉ số lượng giác của góc nhọn (2022) - Toán 9 mới nhất được biên soạn bám sát chương trình Toán 9 giúp các bạn học tốt môn Toán hơn.
Chuyên đề Tỉ số lượng giác của góc nhọn - Toán 9
A. Lý thuyết
1. Khái niệm tỉ số lượng giác của một góc nhọn
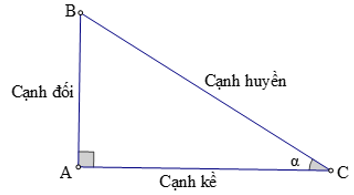
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cos α.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tan α.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cot α.
Ví dụ 1. Cho tam giác ABC có ˆC=α.
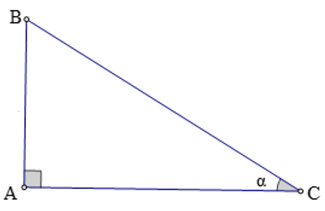
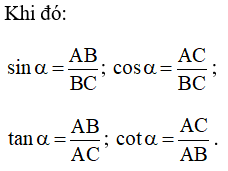
Nhận xét: Nếu α là một góc nhọn thì:
0 < sin α < 1; 0 < cos α < 1; tan α > 0; cot α > 0.
Ví dụ 2. Cho tam giác ABC có ˆC=α
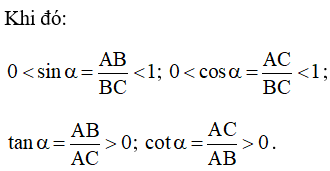
Chú ý: Nếu hai góc nhọn α và β có sin α = sin β (hoặc cos α = cos β, hoặc tan α = tan β, hoặc cot α = cot β) thì α = β vì chúng là hai góc tương ứng của hai tam giác vuông đồng dạng.
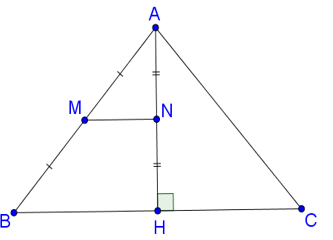
Ví dụ 3. Cho tam giác ABC có AB = AC, đường cao AH. MN là đường trung bình của tam giác ABH. Chứng minh ^AMN=ˆC.
Lời giải:
Vì AH là đường cao của ∆ABC nên AH⊥BC hay AH⊥BH (1)
Mà MN là đường trung bình của ∆AMN nên:
+ AB = 2AM; AH = 2AN.
+ MN // BH (2)
Từ (1) và (2) suy ra MN⊥BH (tính chất từ vuông góc đến song song).

2. Tỉ số lượng giác của hai góc phụ nhau
Định lí. Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Ví dụ 4. Cho tam giác ABC vuông tại A có ˆB=α; ˆC=β.
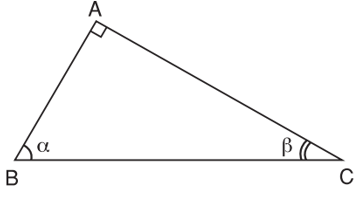
Khi đó, α + β = 90° (trong tam giác vuông hai góc nhọn phụ nhau).
Ta có: sin α = cos β; cos α = sin β; tan α = cot β; cot α = tan β.
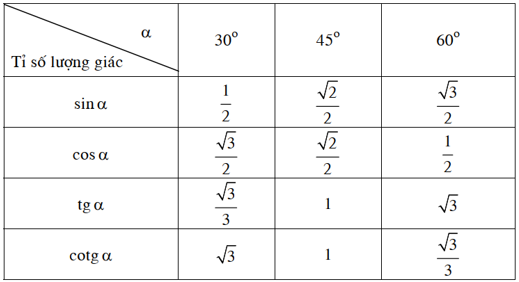
Bảng lượng giác của một số góc đặc biệt:
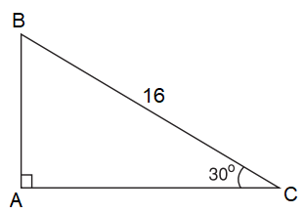
Ví dụ 5. Cho tam giác ABC vuông tại A có BC = 16, ˆC=30o. Tính độ dài AB.
Lời giải:
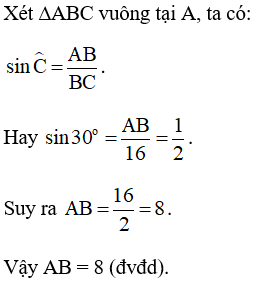
Chú ý: Từ nay khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta bỏ kí hiệu " ^ " đi.
Ví dụ 6. Góc A là góc nhọn thì ta viết sin A thay cho sinˆA.
B. Bài tập
I. Bài tập trắc nghiệm
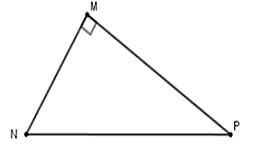
Câu 1: Cho tam giác MNP vuông tại M. Khi đó 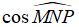
Chọn đáp án A
Câu 2: Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.
Cho α là góc nhọn bất kỳ, khi đó sin2α + cos2α = 1
Chọn đáp án B
Câu 3: Cho α là góc nhọn bất kỳ. Chọn khẳng định sai.
Cho α là góc nhọn bất kỳ, khi đó
Chọn đáp án D
Câu 4: Cho α và β là góc nhọn bất kỳ thỏa mãn α + β = 90° . Chọn khẳng định đúng.
A. α + β = 90°
B. tanα = cotβ
C. tanα = cosα
D. tanα = tanβ
Với hai góc α và β mà α + β = 90 °
sinα = cosβ; cosα = sinβ
tanα = cotβ ; cotα = tanβ
Chọn đáp án B
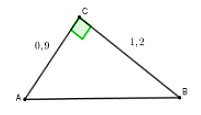
Câu 5: Cho tam giác ABC vuông tại c có BC = 1,2 cm, AC = 0,9 cm . Tính các tỉ số lượng giác sinB; cosB
Chọn đáp án A
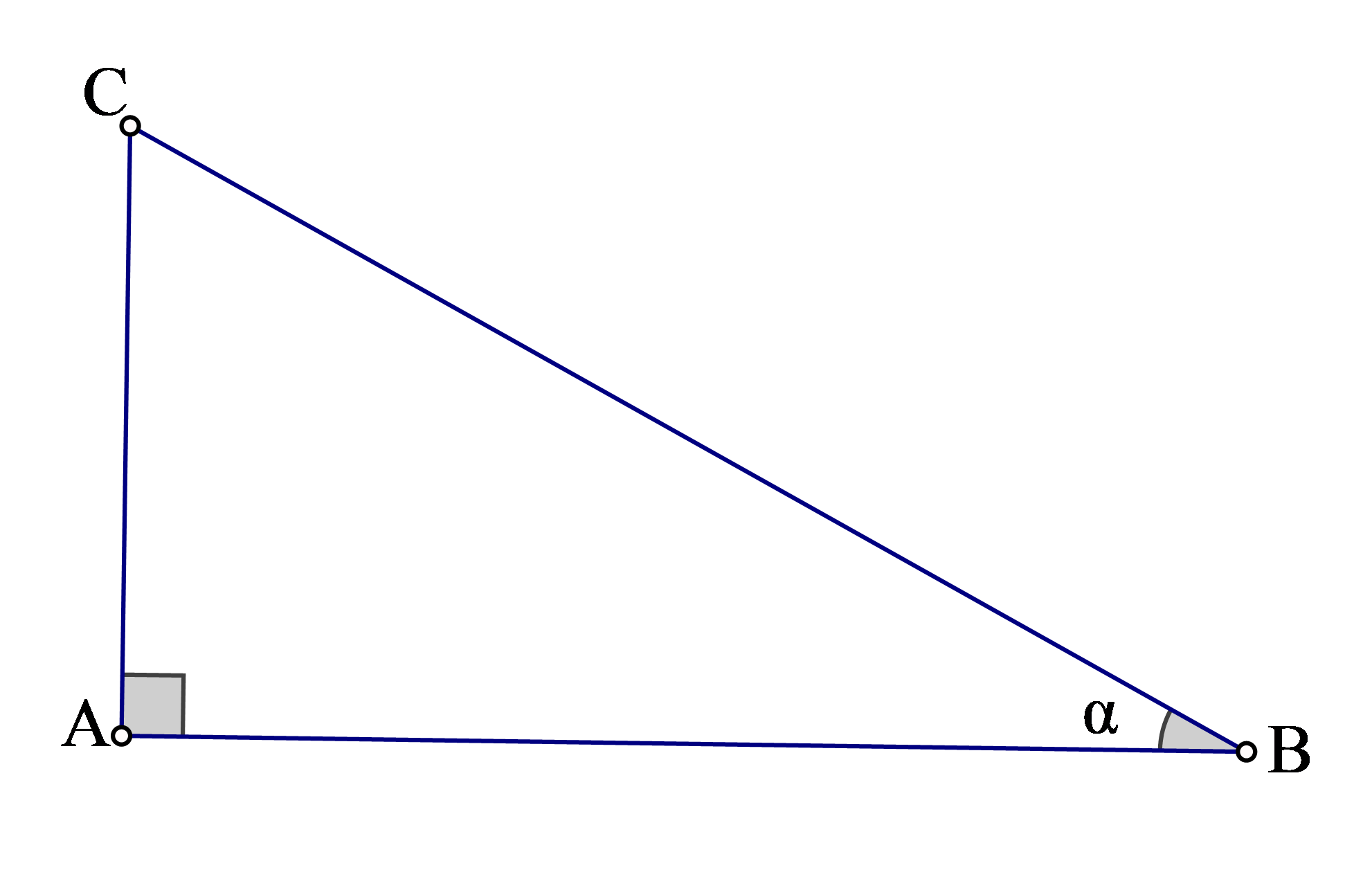
Câu 6: Cho tam giác ABC vuông tại A, AB = 30 cm. Biết tan B = 8/15. Tìm khẳng định sai trong các khẳng định sau :
Chọn đáp án A.
Câu 7: Cho tam giác ABC vuông tại A. Tính
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông ta có:
Chọn đáp án A.
Câu 8: Cho tam giác ABC vuông tại A có đường trung tuyến ứng với cạnh huyền AM = 10 cm; AB = 16 cm . Tính cot B?
Do tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền nên:
Chọn đáp án D.
Áp dụng định lí Pytago vào tam giác ABH vuông tại H ta có:
AH2 + BH2 = AB2
⇔ AH2 = AB2 - BH2 = 132 - 52 = 144
⇔ AH = 12cm
Áp dụng tỉ số lượng giác của nhọn trong tam giác vuông ABH ta có:
Do tam giác BAC là tam giác vuông nên hai góc B và C là 2 góc phụ nhau.
Suy ra:
Chọn đáp án B.
Câu 10: Cho tam giác ABC vuông tại A có AC = 8cm và góc C = 60°. Tính diện tích tam giác ABC .
A. 32 cm2
B. 16√3 cm2
C. 16 cm2
D. 32√3 cm2
Chọn đáp án D.
II. Bài tập tự luận có lời giải
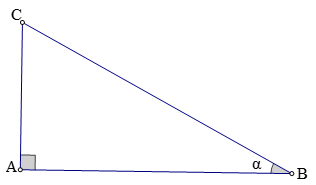
Câu 1: Biết sinα = 5/13. Tính cosα, tanα và cotα.
Lời giải:
Xét ΔABC vuông tại A.
Câu 2: Biết sinα.cosα = 12/25. Tính sinα, cosα.
Lời giải:
Biết sinα.cosα = 12/25. Để tính sinα,cosα ta cần tính sinα + cosα rồi giải phương trình với ẩn là sinα hoặc cosα.
Ta có:
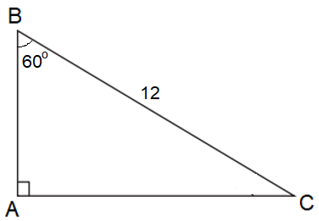
Câu 3: Cho tam giác ABC vuông tại A có ^ABC=60o và BC = 12. Tính độ dài cạnh AC.
Lời giải:
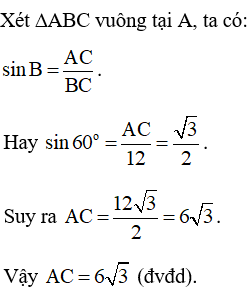
Câu 4: Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn α tùy ý, ta có: sin2 α + cos2 α =1.
Lời giải:
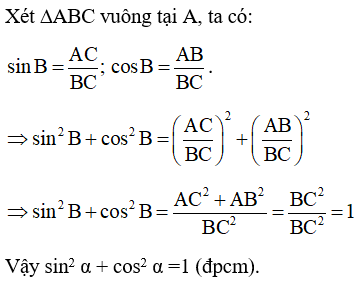
Câu 5: Biết sinα=35. Tính cos α, tan α và cot α.
Lời giải:
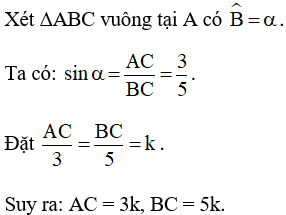
Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:
BC2 = AB2 + AC2
AB2 = BC2 − AC2
AB2 = (5k)2 – (3k)2 = 25k2 – 9k2 = 16k2.
Suy ra: AB = 4k.

Câu 6: Vẽ một tam giác vuông có một góc nhọn bằng 40o rồi viết các tỉ số lượng giác của góc 40o.
Lời giải:
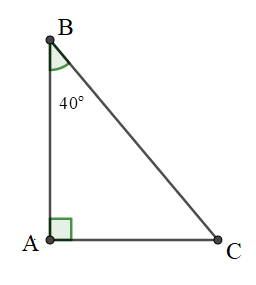
Vẽ tam giác ABC vuông tại A, có:
ˆB=40o , AB = c, AC = b, BC = a
Ta có các tỉ số lượng giác của góc là:
Câu 7: Cho tam giác ABC vuông tại A. Chứng minh rằng: .
Lời giải:
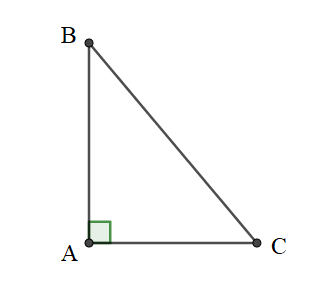
Xét tam giác ABC vuông tại A
Ta có:
(điều cần phải chứng minh)
Câu 8: Cho tam giác ABC vuông tại A, , BC = 8cm. Hãy tính cạnh AB (làm tròn đến chữ số thập phân thứ ba), biết rằng
Lời giải:
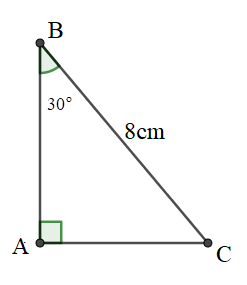
Xét tam giác ABC vuông tại A
BC = 8cm
Ta có:
Câu 9: Cho tam giác ABC vuông tại A, AB = 6cm, (h.9). Biết , hãy tính
a) Cạnh AC
b) Cạnh BC
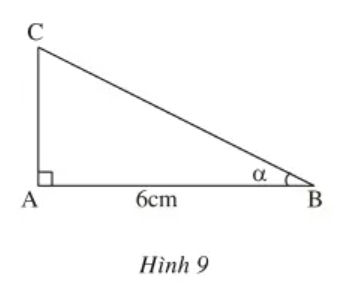
Lời giải:
a)
Xét tam giác ABC vuông tại A
AB = 6cm,
Ta có:
b)
Xét tam giác ABC vuông tại A
Áp dụng định lí Py-ta-go ta có:
(cm)
Câu 10: Cho tam giác ABC vuông tại A, trong đó AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.
Lời giải:
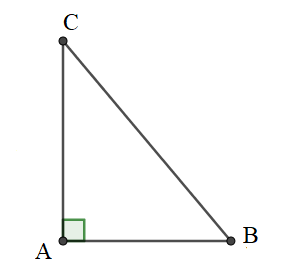
Xét tam giác ABC vuông tại A
AB = 6cm, AC = 8cm
Áp dụng định lí Py-ta-go ta có:
Ta có các tỉ số lượng giác của góc B.
Có
Do đó, góc B và góc C là hai góc phụ nhau nên ta có:
III. Bài tập vận dụng
Câu 1: Cho tam giác ABC vuông tại A có BC = 9cm; AC = 5cm. Tính tỉ số lượng giác tan C (làm tròn đến chữ số thập phân thứ 1)
Câu 2: Cho tam giác ABC vuông tại A, đường cao AH có AB = 13cm, BH = 0,5dm. Tính tỉ số lượng giác sinC (làm tròn đến chữ số thập phân thứ 2)
Câu 3: Cho tam giác ABC vuông tại A, đường cao AH có AC = 15cm, CH = 6cm. Tính tỉ số lượng giác cos B.
Câu 4: Cho tam giác ABC vuông tại A, đường cao AH có CH = 4cm, BH = 3cm. Tính tỉ số lượng giác cos C (làm tròn đến chữ số thập phân thứ 2)
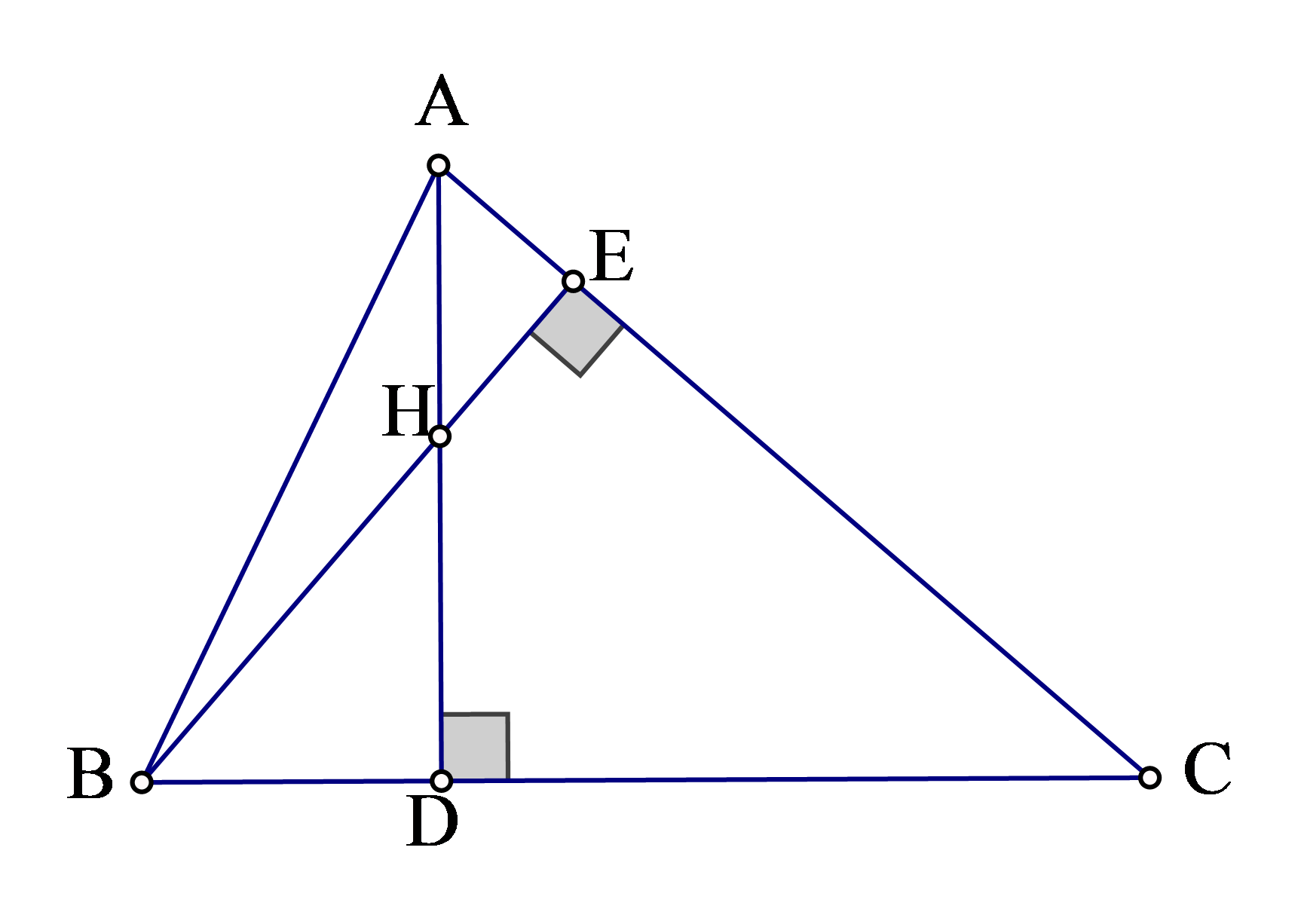
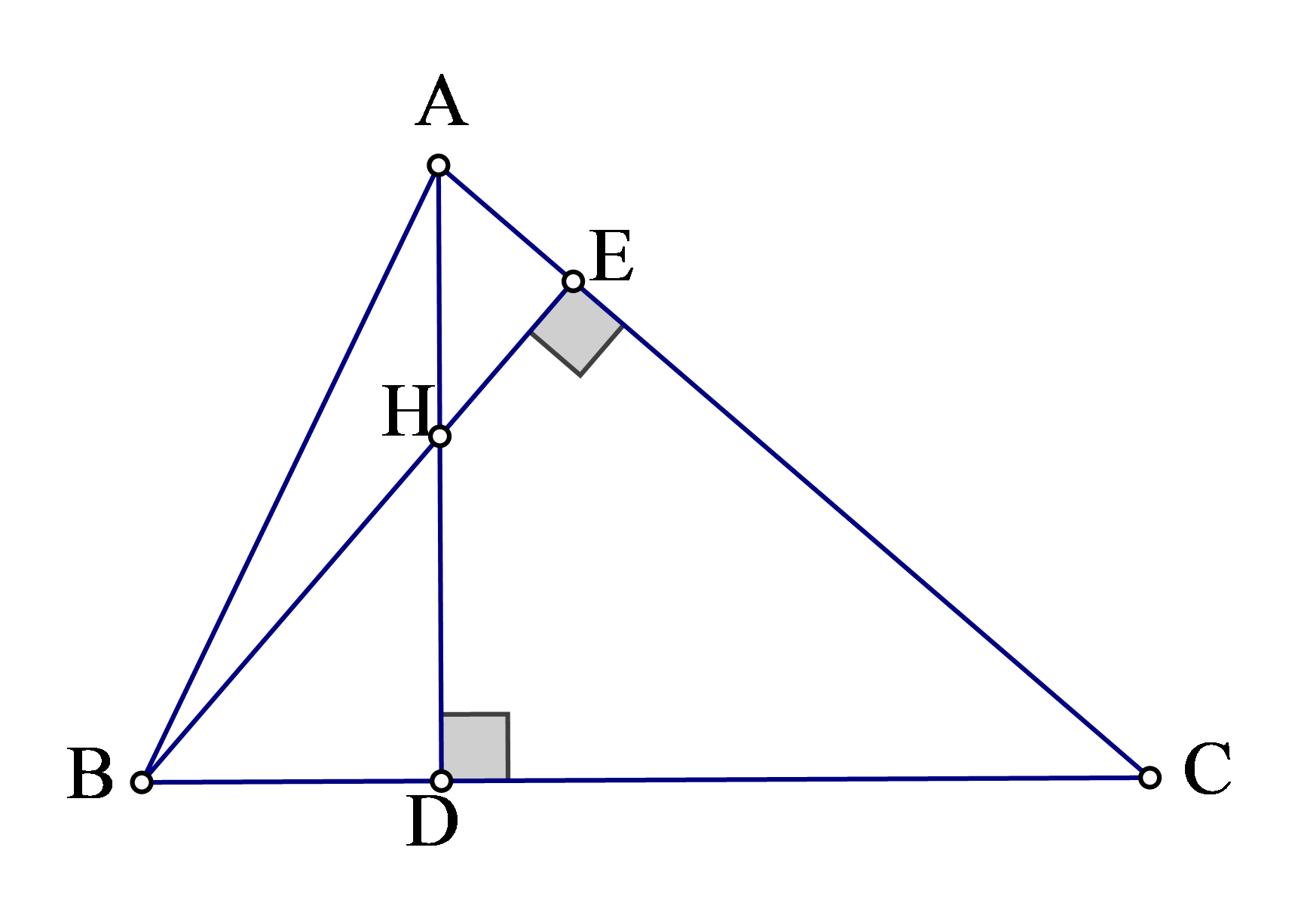
Câu 5: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2 . Chứng minh rằng tgB.tgC = 3 .
Câu 6: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng:
Câu 7: Cho tam giác ABC vuông tại A. Biết AB=6cm, BC=10cm. Tính , , , .
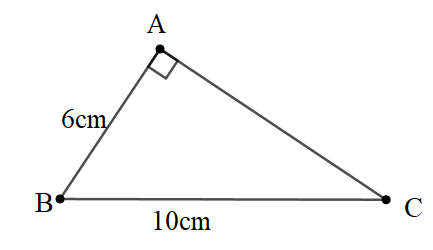
Câu 8: Cho tam giác ABC vuông tại A. Có AB=3cm, AC=4cm. Tính , , , .
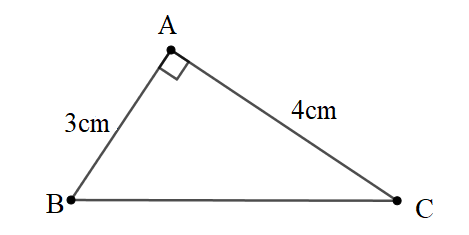
Câu 9: Cho tam giác ABC. Có đường cao AH ứng với cạnh BC. AH=5cm, AB=7cm. Tính
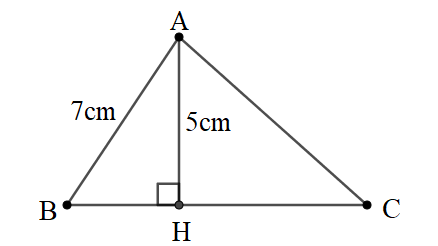
Câu 10: Cho tam giác ABC có hai cạnh góc vuông là AB = 16mm và AC = 3cm.
a, Tính tỉ số lượng giác của các góc nhọn.
b, Tính tổng sinB + sinC
Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:
Chuyên đề Một số hệ thức về cạnh và góc trong tam giác vuông
Chuyên đề Ứng dụng thực tế các tỉ số lượng giác của góc nhọn
Chuyên đề Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Xem thêm các chương trình khác:
- Giải sgk Hóa học 9 (sách mới) | Giải bài tập Hóa 9
- Giải sbt Hóa học 9
- Giải vở bài tập Hóa học 9
- Lý thuyết Hóa học 9
- Các dạng bài tập Hóa học lớp 9
- Tóm tắt tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 9 (hay nhất) | Để học tốt Ngữ văn 9 (sách mới)
- Soạn văn 9 (ngắn nhất)
- Văn mẫu 9 (sách mới) | Để học tốt Ngữ văn 9 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 9 (sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Tiếng Anh 9 (thí điểm)
- Giải sgk Tiếng Anh 9 (sách mới) | Để học tốt Tiếng Anh 9
- Giải sbt Tiếng Anh 9
- Giải sbt Tiếng Anh 9 (thí điểm)
- Giải sgk Sinh học 9 (sách mới) | Giải bài tập Sinh học 9
- Giải vở bài tập Sinh học 9
- Lý thuyết Sinh học 9
- Giải sbt Sinh học 9
- Giải sgk Vật Lí 9 (sách mới) | Giải bài tập Vật lí 9
- Giải sbt Vật Lí 9
- Lý thuyết Vật Lí 9
- Các dạng bài tập Vật lí lớp 9
- Giải vở bài tập Vật lí 9
- Giải sgk Địa Lí 9 (sách mới) | Giải bài tập Địa lí 9
- Lý thuyết Địa Lí 9
- Giải Tập bản đồ Địa Lí 9
- Giải sgk Tin học 9 (sách mới) | Giải bài tập Tin học 9
- Lý thuyết Tin học 9
- Lý thuyết Giáo dục công dân 9
- Giải vở bài tập Lịch sử 9
- Giải Tập bản đồ Lịch sử 9
- Lý thuyết Lịch sử 9
- Lý thuyết Công nghệ 9