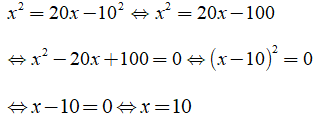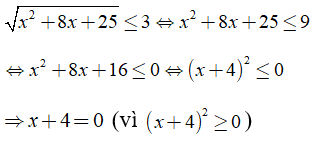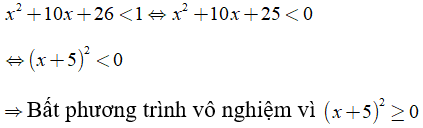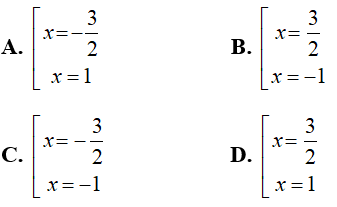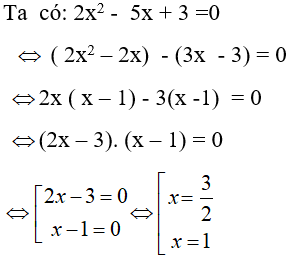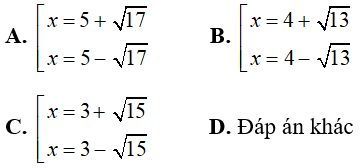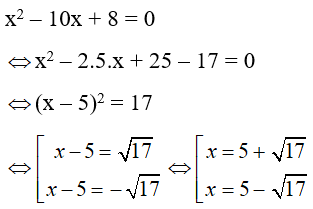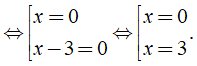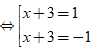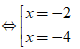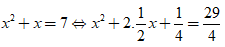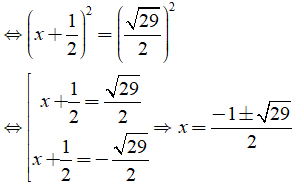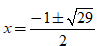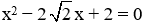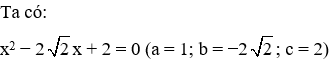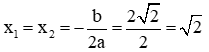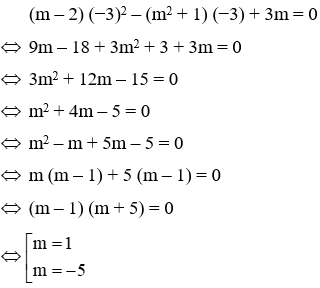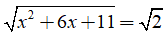Chuyên đề Phương trình bậc hai một ẩn (2022) - Toán 9

Chuyên đề Phương trình bậc hai một ẩn - Toán 9

A. Lý thuyết

1. Định nghĩa

Định nghĩa: Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng

${\mathrm{ax}}^2+\mathrm{bx}+\mathrm{c}=0$

trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và $\mathrm{a}\ne 0$.

Ví dụ 1:

a) ${\mathrm{x}}^2-2\mathrm{x}+1=0$ là một phương trình bậc hai với a = 1; b = -2; c = 1.

b) ${\mathrm{x}}^2-9=0$ là một phương trình bậc hai với a = 1; b = 0; c = -9.

2. Một số ví dụ về giải phương trình bậc hai

a) Trường hợp b = 0.

Với trường hợp b = 0 thì khi đó phương trình bậc hai của chúng ta là ${\mathrm{ax}}^2+\mathrm{c}=0$

+ Nếu a và c cùng dấu thì phương trình sẽ vô nghiệm

Ví dụ 2: $3{\mathrm{x}}^2+9=0\iff 3{\mathrm{x}}^2=-9$ (vô lí)

+ Nếu a và c trái dấu thì phương trình sẽ có hai nghiệm

Ví dụ 3: ${\mathrm{x}}^2-4=0\iff {\mathrm{x}}^2=4\iff \mathrm{x}=\pm 2$.

b) Trường hợp c = 0.

Với trường hợp c = 0 thì khi đó phương trình bậc hai của chúng ta là ${\mathrm{ax}}^2+\mathrm{bx}=0$

Khi đó phương trình luôn có hai nghiệm là x = 0 và x = $\mathrm{x}=\frac{-\mathrm{b}}{\mathrm{a}}$.

Ví dụ 4: ${\mathrm{x}}^2-3\mathrm{x}=0$

$$\begin{gathered} \iff \mathrm{x}\left(\mathrm{x}-3\right)=0 \\ \iff \left\{\begin{array}{l}\mathrm{x}=0\\ \mathrm{x}-3=0\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=0\\ \mathrm{x}=3\end{array}\right.\right. \end{gathered}$$

c) Trường hợp $\mathrm{a}\ne 0; \mathrm{b}\ne 0; \mathrm{c}\ne 0$.

Khi đó ta sẽ biến đổi phương trình ${\mathrm{ax}}^2+\mathrm{bx}+\mathrm{c}=0$ thành tổng của một bình phương với một số.

Ví dụ 5: ${\mathrm{x}}^2-4\mathrm{x}+3=0$

$$\begin{gathered} \iff {\mathrm{x}}^2-4\mathrm{x}+4-1=0 \\ \iff {\left(\mathrm{x}-2\right)}^2-1=0 \\ \iff {\left(\mathrm{x}-2\right)}^2=1 \end{gathered}$$

B. Bài tập

I. Bài tập trắc nghiệm

Câu 1: Hệ số c của phương trình x2 + 7x + 9 = 9 là?

A. 9

B. -9

C. 0

D. 18

Lời giải:

Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0. Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.

Khi đó ta có:

Do đó hệ số c là x2 + 7x + 9 = 9 ⇔ x2 + 7x = 0

Chọn đáp án C.

Câu 2: Trong các phương trình sau, phương trình nào là phương trình bậc hai?

A. x2 + 4x - 7 = x2 + 8x - 10

B. x3 + 8x = 0

C. x2 - 4 = 0

D. 5x - 1 = 0

Lời giải:

Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0 .Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0 .

+ x2 + 4x - 7 = x2 + 8x - 10 ⇔ 4x - 3 = 0 . Loại vì đây là phương trình bậc nhất

+ x3 + 8x = 0 vì mũ cao nhất của x là 3 nên không là phương trình bậc hai.

+ x2 - 4 = 0 là phương trình bậc hai thỏa mãn

+ 5x - 1 = 0 là phương trình bậc nhất một ẩn

Chọn đáp án C.

Câu 3: Số nghiệm của phương trình x2 = 20x - 102 là?

A. 1 nghiệm

B. 2 nghiệm

C. Vô số nghiệm

D. Vô nghiệm

Lời giải:

Ta có:

Vậy phương tình đã cho có 1 nghiệm

Chọn đáp án A.

Câu 4: Tập nghiệm của bất phương trình Toán lớp 9 | Lý thuyết - Bài tập Toán 9 có đáp án

A. x > -4

B. x < -4

C. x ≤ -4

D. x = -4

Lời giải:

Ta có:

Suy ra x = -4

Chọn đáp án D.

Câu 5: Tập nghiệm của bất phương trình x2 + 10x + 26 < 1

A. x ≥ -5

B. x ≤ -5

C. x = -5

D. Vô nghiệm

Lời giải:

Ta có:

Bất phương trình vô nghiệm vì

Chọn đáp án D.

Câu 6: Cho phương trình 2x2 – 10x + 100 = -2x + 10. Sau khi đưa phương trình trên về dạng ax2 + bx + c = 0 thì hệ số b là?

A. -8

B . -12

C. 12

D. 8

Lời giải:

Ta có:

2x2 – 10x + 100 = -2x + 10

⇔ 2x2 – 10x +100 + 2x -10 =0

⇔ 2x2 – 8x + 90 = 0

Đây là phương trình bậc hai một ẩn có a = 2; b = - 8 và c = 90 .

Chọn đáp án A.

Câu 7: Cho phương trình 2x3 + 2x2 - 3x + 10 = 2x3 + x2 – 10. Sau khi biến đổi đưa phương trình trên về dạng ax2 + bx+ c =0 thì hệ số a bằng ?

A. 2

B.1

C. 3

D. -1

Lời giải:

Ta có : 2x3 + 2x2 - 3x + 10 = 2x3 + x2 – 10

⇔ 2x3 + 2x2 - 3x + 10 - 2x3 - x2 + 10= 0

⇔ x2 – 3x + 20 = 0

Phương trình trên là phương trình bậc hai một ẩn với a = 1; b = -3 và c = 20.

Chọn đáp án B.

Câu 8: Giải phương trình sau: 2x2 - 5x + 3 = 0

Lời giải:

Chọn đáp án D.

Câu 9: Giải phương trình -10x2 + 40 = 0

A. Vô nghiệm

B. x = 2

C. x = 4

D . x = ±2

Lời giải:

Ta có: -10x2 + 40 = 0

⇔ -10x2 = - 40 ⇔ x 2 = 4

⇔ x = ±2

Chọn đáp án C.

Câu 10: Giải phương trình x2 - 10x + 8 = 0

Lời giải:

Ta có:

Chọn đáp án A.

II. Bài tập tự luận có lời giải

Câu 1: Giải phương trình x2 - 3x = 0

Lời giải:

Ta có: x2 - 3x = 0 ⇔ x(x - 3) = 0

     

Vậy phương trình có hai nghiệm là x1 = 0; x2 = 3

Câu 2: Đưa các phương trình sau về dạng ax2 + bx + c = 0 rồi chỉ rõ các hệ số a, b, c của phương trình ấy. Các phương trình: 5x2 - 3x = 10x + 100; x2 = 900

Lời giải:

+ Ta có: 5x2 - 3x = 10x + 100 ⇔ 5x2 - 13x - 100 = 0

Hệ số a = 5; b = -13; c = -100

+ Ta có: x2 = 900 ⇔ x2 - 900 = 0

Hệ số a = 1, b = 0; c = -900

Câu 3: Giải các phương trình sau bằng cách thêm bớt thích hợp

a) x2 + 6x = -8

b) x2 + x = 7

Lời giải:

a) Ta có: x2 + 6x = -8 ⇔ x2 + 6x + 9 = -8 + 9

⇔ (x + 3)2 = 1 

Vậy phương trình đã cho có x = -2 hoặc x = -4

b) Ta có: 

Vậy phương trình đã cho có nghiệm là 

Câu 4: Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: −13x2 + 22x − 13 = 0

Lời giải:

Ta có: 

−13x2 + 22x − 13 = 0 (a = −13; b = 22; x = −13)

⇒ ∆ = b2 – 4ac = 222 – 4.(−13). (−13) = −192 < 0 nên phương trình vô nghiệm

Câu 5: Tính biệt thức ∆ từ đó tìm các nghiệm (nếu có) của phương trình 

Lời giải:

 nên phương trình có nghiệm kép

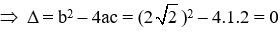
Câu 6: Tìm tích các giá trị của m để phương trình 4mx2 − x – 14m2 = 0 có nghiệm x = 2

Lời giải:

Thay x = 2 vào phương trình 4mx2 – x – 10m2 = 0, ta có:

Câu 7: Tìm tổng các giá trị của m để phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0 có nghiệm x = −3

Lời giải:

Thay x = −3 vào phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:

Suy ra tổng các giá trị của m là (−5) + 1 = −4

Câu 8 Tính biệt thức ∆ từ đó tìm số nghiệm của phương trình: 9x2 − 15x + 3 = 0

Lời giải:

Ta có: 9x2 − 15x + 3 = 0 (a = 9; b = −15; c = 3)

⇒ ∆ = b2 – 4ac = (−15)2 – 4.9.3 = 117 > 0 nên phương trình có hai nghiệm phân biệt

Câu 9: Các phương trình sau đây đâu là phương trình bậc hai một ẩn? Chỉ rõ hệ số a; b; c.

a) ${\left(\mathrm{x}+3\right)}^2-2{\mathrm{x}}^2=0$

b) $2{\left(\mathrm{x}-3\right)}^2-2{\mathrm{x}}^2=0$

c) $4{\mathrm{x}}^2-16=0$

Lời giải:

a) ${\left(\mathrm{x}+3\right)}^2-2{\mathrm{x}}^2=0$

$$\begin{gathered} \iff {\mathrm{x}}^2+6\mathrm{x}+9-2{\mathrm{x}}^2=0 \\ \iff -{\mathrm{x}}^2+6\mathrm{x}+9=0 \end{gathered}$$

Đây là phương trình bậc hai một ẩn với a = -1; b = 6; c = 9.

b) $2{\left(\mathrm{x}-3\right)}^2-2{\mathrm{x}}^2=0$

$$\begin{gathered} \iff 2\left({\mathrm{x}}^2-6\mathrm{x}+9\right)-2{\mathrm{x}}^2=0 \\ \iff 2{\mathrm{x}}^2-12\mathrm{x}+18-2{\mathrm{x}}^2=0 \end{gathered}$$

$\iff 0{\mathrm{x}}^2-12\mathrm{x}+18=0$ đây không phải phương trình bậc hai một ẩn vì a = 0.

c) $4{\mathrm{x}}^2-16=0$

Đây là phương trình bậc hai một ẩn với a = 4; b = 0; c = -16

Câu 10: Giải các phương trình bậc hai sau:

a) ${\mathrm{x}}^2-6\mathrm{x}=0$

b) ${\mathrm{x}}^2+4=0$

c) ${\mathrm{x}}^2-5\mathrm{x}+6=0$

Lời giải:

a) ${\mathrm{x}}^2-6\mathrm{x}=0$

$$\begin{gathered} \iff \mathrm{x}\left(\mathrm{x}-6\right)=0 \\ \iff \left\{\begin{array}{l}\mathrm{x}=0\\ \mathrm{x}-6=0\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=0\\ \mathrm{x}=6\end{array}\right.\right. \end{gathered}$$

Vậy phương trình đã cho có tập nghiệm là S = {0; 6}.

b) ${\mathrm{x}}^2+4=0$

$\iff {\mathrm{x}}^2=-4$ (vô lí)

Vậy phương trình vô nghiệm.

c) ${\mathrm{x}}^2-5\mathrm{x}+6=0$

$$\begin{gathered} \iff {\mathrm{x}}^2-2.\mathrm{x}.\frac{5}{2}+{\left(\frac{5}{2}\right)}^2-{\left(\frac{5}{2}\right)}^2+6=0 \\ \iff {\left(\mathrm{x}-\frac{5}{2}\right)}^2-\frac{1}{4}=0 \\ \iff {\left(\mathrm{x}-\frac{5}{2}\right)}^2={\left(\frac{1}{2}\right)}^2={\left(\frac{-1}{2}\right)}^2 \\ \iff \left\{\begin{array}{l}\mathrm{x}-\frac{5}{2}=\frac{1}{2}\\ \mathrm{x}-\frac{5}{2}=\frac{-1}{2}\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=\frac{5}{2}+\frac{1}{2}\\ \mathrm{x}=\frac{5}{2}-\frac{1}{2}\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=3\\ \mathrm{x}=2\end{array}\right.\right.\right. \end{gathered}$$

Vậy phương trình đã cho có nghiệm S = {2; 3}.

III. Bài tập vận dụng

Câu 1: Giải phương trình bằng cách phân tích đa thức thành nhân tử x2 - 7x + 12 = 0

Câu 2: Giải phương trình 

Câu 3: Xác định tập nghiệm của phương trình x² + 3x - 1 = 0

Câu 4: Tìm nghiệm của phương trình 3x² + 7x + 2 = 0

Câu 5: Xác định tập nghiệm của phương trình x² - 2mx + m = 0 với m =1

Câu 6: Cho phương trình bậc hai (m - 1)x² - 2mx + m + 1 = 0 (m là tham số). Xác định các giá trị nguyên của m để phương trình có nghiệm nguyên 

Câu 7: Phương trình x² + (2m + 1)x + 3m = 0 (với m là tham số) có hai nghiệm phân biệt, trong đó có một nghiệm là x₁ = 3, nghiệm còn lại là x₂ bằng bao nhiêu?

Câu 8: Tìm hệ thức liên hệ giữa hai nghiệm của phương trình x² - (m + 3)x + 2m - 5 = 0 không phụ thuộc vào m.

Câu 9: Cho phương trình x² - 2x - 8 = 0 có hai nghiệm x₁ và x₂. Xác định phương trình bậc hai một ẩn có hai nghiệm là y₁ = x₁ - 3 và y₂ = x₂ - 3 

Câu 10: Giải phương trình x² - 2x + 1 - m² = 0 với m là tham số, m ≠ 0.

Xem thêm các bài Chuyên đề Toán lớp 9 hay, chi tiết khác:

Chuyên đề Công thức nghiệm của phương trình bậc hai

Chuyên đề Công thức nghiệm thu gọn

Chuyên đề Hệ thức Vi – ét và ứng dụng

Chuyên đề Phương trình quy về phương trình bậc hai

Chuyên đề Giải bài toán bằng cách lập phương trình