Toán 7 Bài 16 (Kết nối tri thức): Tam giác cân. Đường trung trực của đoạn thẳng
Với giải bài tập Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 16.
Giải bài tập Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Video giải bài tập Toán 7 Bài 16 Tam giác cân. Đường trung trực của đoạn thẳng
Mở đầu
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
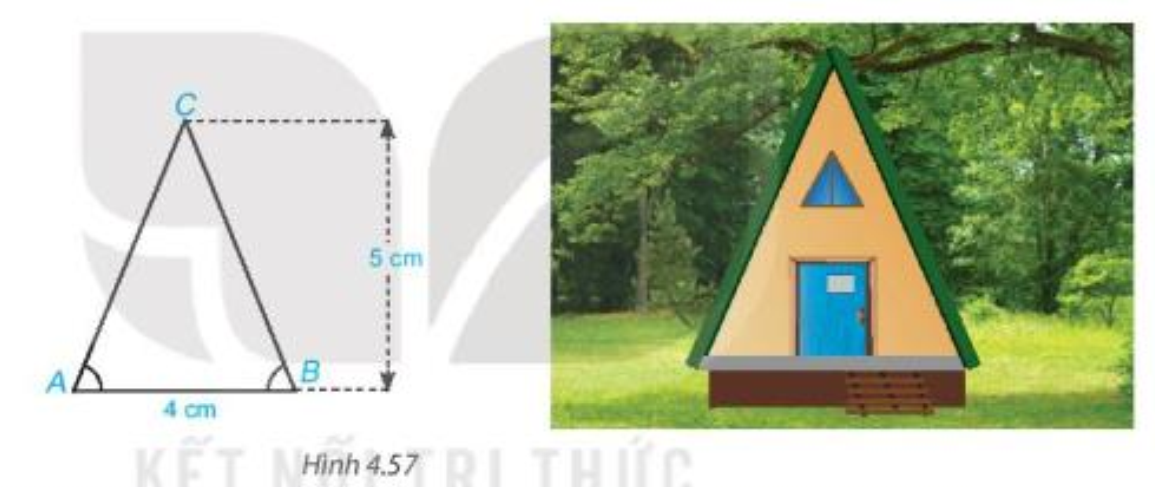
Để xác định được chính xác điểm C trên bản thiết kế ta sẽ làm các bước sau:
Bước 1. Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 4 cm.

Bước 2. Vẽ đường trung trực d của đoạn thẳng AB (đường thẳng d vuông góc với AB tại trung điểm O của đoạn thẳng AB).
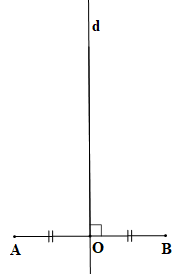
Bước 3. Trên đường trung trực d lấy điểm C sao cho OC = 5 cm.
Vì C nằm trên trung trực d của đoạn thẳng AB nên CA = CB (tính chất đường trung trực).
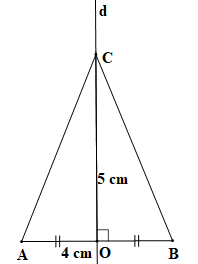
Khi đó trên bản thiết kế tỉ lệ 1 : 100 đã thể hiện được ngôi nhà cao 5 m, bề ngang mặt sàn rộng 4 m với hai mái nghiêng như nhau.
1.Tam giác cân và tính chất
Lời giải:
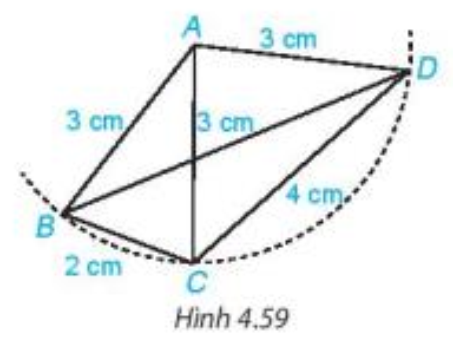
Tam giác ABC có AB = AC = 3 cm nên tam giác ABC cân tại A, với hai cạnh bên là AB và AC, cạnh đáy là BC, góc ở đỉnh là A, hai góc ở đáy là và
Tam giác ABD có AB = AD = 3 cm nên tam giác ABD cân tại A, với hai cạnh bên là AB và AD, cạnh đáy là BD, góc ở đỉnh là A, hai góc ở đáy là và
Tam giác ACD có AC = AD = 3 cm nên tam giác ACD cân tại A, với hai cạnh bên là AC và AD, cạnh đáy là CD, góc ở đỉnh là A, hai góc ở đáy là và
a) Chứng minh rằng theo trường hợp cạnh – cạnh – cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Lời giải:
|
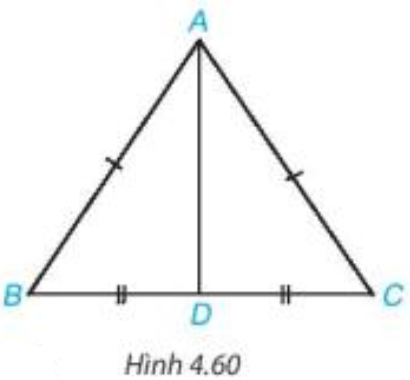
GT |
cân tại A, D là trung điểm của BC. |
|
KL |
a) (c.c.c); b) và của tam giác ABC có bằng nhau không? |
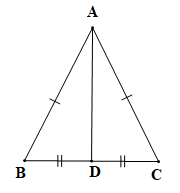
Chứng minh (hình vẽ trên):
a) Tam giác ABC cân tại A (theo giả thiết) nên ta có AB = AC (định nghĩa tam giác cân).
Xét tam giác ABD và tam giác ACD có:
AB = AC (chứng minh trên);
BD = CD (do D là trung điểm của BC);
AD là cạnh chung.
Vậy (c.c.c).
b) Từ (chứng minh câu a) suy ra (hai góc tương ứng).
Hay .
Vậy góc và của tam giác ABC cân tại A bằng nhau.
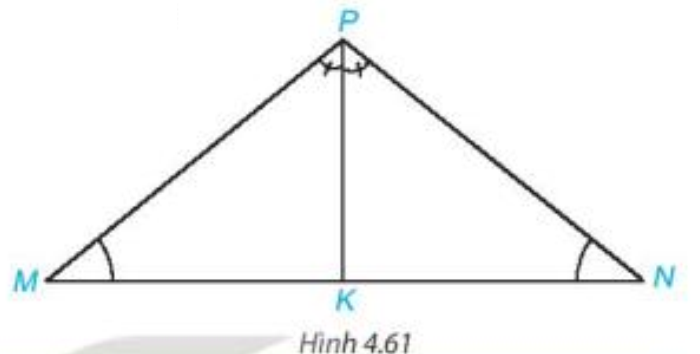
Cho tam giác MNP có Vẽ tia phân giác PK của góc MPN ().
c) Tam giác MNP có cân tại P không?
Lời giải:
|
GT |
, ; PK là tia phân giác của góc MPN. |
|
KL |
a) b) c) Tam giác MNP có cân tại P không? |
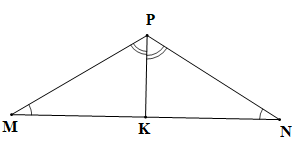
Chứng minh (hình vẽ trên):
a) PK là tia phân giác của góc MPN (theo giả thiết) nên (tính chất tia phân giác của một góc).
Tam giác MPK có là góc ngoài của tam giác tại đỉnh K nên ta có
Tam giác NPK có là góc ngoài của tam giác tại đỉnh K nên ta có
Mà (chứng minh trên) và (theo giả thiết).
Do đó
b) Xét tam giác MPK và tam giác NPK có:
(chứng minh ở câu a);
PK là cạnh chung;
(chứng minh ở câu a).
Vậy (g.c.g).
c) Từ (chứng minh ở câu b) suy ra MP = NP (hai cạnh tương ứng).
Do đó tam giác MNP cân tại P (định nghĩa tam giác cân).
Vậy tam giác MNP cân tại P.
Lời giải:
|
GT |
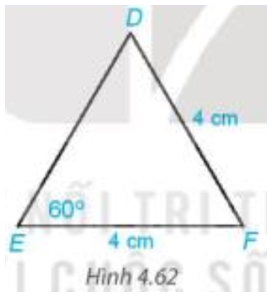
, EF = DF = 4 cm, . |
|
KL |
Tính số đo và độ dài cạnh DE. |
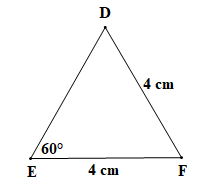
Tam giác DEF có EF = DF = 4 cm (theo giả thiết) nên tam giác DEF cân tại F (định nghĩa tam giác cân).
Do đó (tính chất tam giác cân).
Mà (theo giả thiết) nên .
Tam giác DEF có , , áp dụng định lí tổng ba góc trong một tam giác ta có .
Suy ra
Hay
Khi đó ta có .
Suy ra tam giác DEF cân tại D (dấu hiệu nhận biết tam giác cân).
Do đó DE = DF (định nghĩa tam giác cân).
Mà DF = 4 cm (theo giả thiết).
Vậy DE = 4 cm.
Thử thách nhỏ trang 81 Toán 7 Tập 1:
Một tam giác có gì đặc biệt nếu thỏa mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau.
b) Tam giác cân có một góc bằng 60o.
Lời giải:
a)
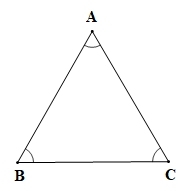
Áp dụng định lí tổng ba góc trong tam giác cho tam giác ABC ta có
Mà (theo giả thiết);
Suy ra hay .
Do đó
Khi đó .
Tam giác ABC có ba góc bằng nhau và cùng bằng 60° nên là tam giác đều.
b) +) Tam giác DEF cân tại D có
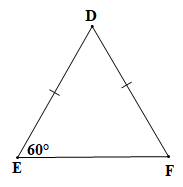
Tam giác DEF cân tại D (theo giả thiết) nên (tính chất tam giác cân).
Mà do đó
Tam giác DEF có , , áp dụng định lí tổng ba góc trong một tam giác ta có .
Suy ra
Hay
Khi đó ta có .
Tam giác DEF có ba góc bằng nhau và cùng bằng 60° nên là tam giác đều.
+) Tam giác MNP cân tại M có
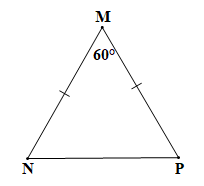
Tam giác MNP cân tại M (theo giả thiết) nên (tính chất tam giác cân).
Tam giác MNP có , , áp dụng định lí tổng ba góc trong một tam giác ta có .
Suy ra
Hay
.
Khi đó .
Tam giác MNP có ba góc bằng nhau và cùng bằng 60° nên là tam giác đều.
2. Đường trung trực của một đoạn thẳng
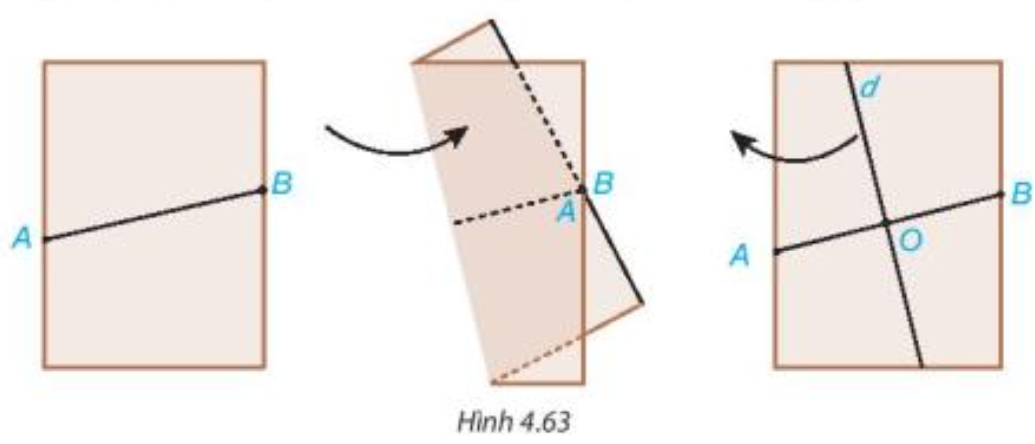
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau.
Mở mảnh giấy ra, kẻ đường thẳng d theo nếp gấp.
a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?
b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
Lời giải:
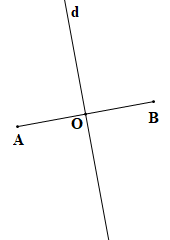
Mảnh giấy sau khi gấp được mô tả như hình vẽ trên.
a) Mảnh giấy được gấp sao cho điểm A trùng với điểm B, O là giao điểm của đường thẳng d và AB, khi đó đường thẳng d chia đoạn thẳng AB thành hai đoạn bằng nhau, tức là OA = OB.
Do đó O là trung điểm của đoạn thẳng AB.
b) Dùng thước đo góc ta thấy góc dOB có số đo bằng 90° nên
Vậy đường thẳng d vuông góc với AB.
Lời giải:
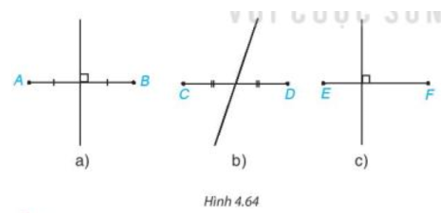
Trong các hình vẽ trên:
Hình 4.64 a) ta thấy Lan đã vẽ đường thẳng vuông góc với AB tại trung điểm của AB nên đường thẳng này là đường trung trực của đoạn thẳng AB.
Hình 4.64 b) Lan vẽ đường thẳng đi qua trung điểm của CD nhưng không vuông góc với CD do đó đường thẳng này không phải là trung trực của đoạn thẳng CD.
Trên Hình 4.64 c) Lan vẽ đường thẳng vuông góc với EF nhưng không đi qua trung điểm của EF do đó đường thẳng này không phải là đường trung trực của đoạn thẳng EF.
Vậy hình bạn Lan vẽ đúng là hình a.
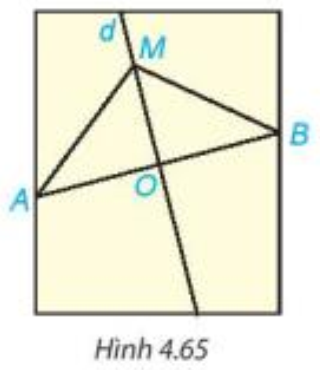
Lời giải:
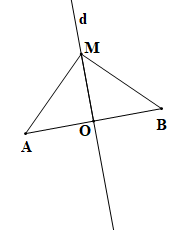
Dùng thước thẳng có vạch chia ta đo độ dài các đoạn thẳng AM và BM, sau đó so sánh kết quả thì thấy độ dài của hai đoạn thẳng này bằng nhau.
Vậy AM = BM.
Lời giải:
|
GT |
Đoạn thẳng AB, d là đường trung trực của AB; AM = 3 cm, . |
|
KL |
Tính BM và số đo góc MBA. |
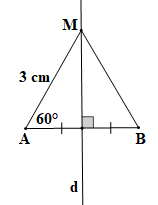
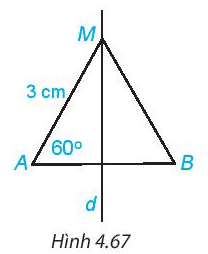
Điểm M nằm trên đường trung trực d của đoạn thẳng AB nên ta có MA = MB (tính chất đường trung trực của một đoạn thẳng).
Mà MA = 3 cm nên MB = 3 cm.
Do MA = MB (chứng minh trên) nên tam giác MAB cân tại M (định nghĩa tam giác cân).
Suy ra (tính chất tam giác cân).
Mà do đó
Vậy BM = 3 cm,
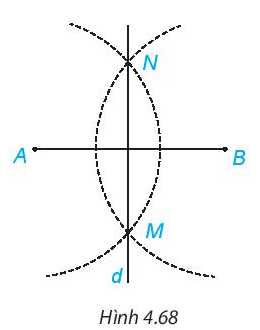
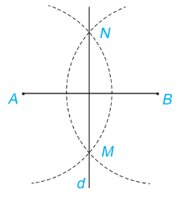
- Dùng thước thẳng vẽ đường thẳng MN. Khi đó MN là đường trung trực của đoạn thẳng AB (H.4.68).
Lời giải:
Bước 1. Dùng thước thẳng vẽ đoạn thẳng AB ta được hình vẽ sau:
![]()
Bước 2. Dùng compa vẽ cung tròn tâm A và cung tròn tâm B có cùng bán kính (bán kính lớn hơn ).
Hai cung tròn này cắt nhau tại hai điểm M và N, do đó AN = AM = BN = BM.
Khi đó ta được hình vẽ sau:
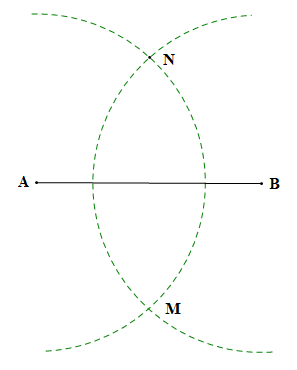
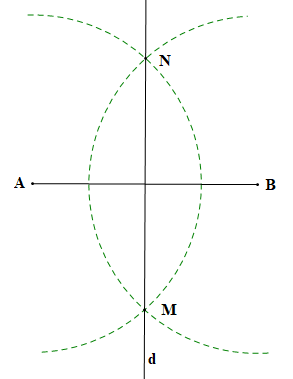
Bước 3. Dùng thước thẳng vẽ đường thẳng đi qua hai điểm M và N ta được hình vẽ dưới đây.
AN = BN nên N nằm trên đường trung trực của AB.
AM = BM nên M nằm trên đường trung trực của AB.
Khi đó đường thẳng MN là đường trung trực của đoạn thẳng AB.
Bài tập
Lời giải:
|
GT |
cân tại A, |
|
KL |
BE = CF. |
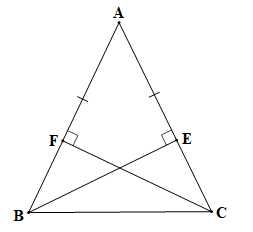
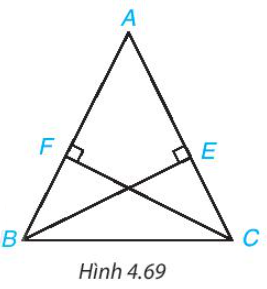
Chứng minh (hình vẽ trên):
Tam giác ABC cân tại A (theo giả thiết) nên AB = AC (định nghĩa tam giác cân).
Vì (theo giả thiết) nên , do đó tam giác AEB vuông tại E.
Vì (theo giả thiết) nên , do đó tam giác AFC vuông tại F.
Xét tam giác AEB (vuông tại E) và tam giác AFC (vuông tại F) có:
AB = AC (chứng minh trên);
là góc chung.
Vậy (cạnh huyền – góc nhọn).
Suy ra BE = CF (hai cạnh tương ứng).
Vậy BE = CF.
Lời giải:
|
GT |
cân tại A, M là trung điểm BC. |
|
KL |
và AM là tia phân giác của góc BAC. |
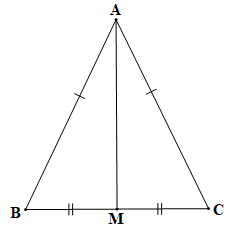
Chứng minh (hình vẽ trên):
Tam giác ABC cân tại A (theo giả thiết) nên AB = AC (định nghĩa tam giác cân).
Xét tam giác ABM và tam giác ACM có:
AB = AC (chứng minh trên);
BM = CM (do M là trung điểm của BC);
AM là cạnh chung.
Vậy (c.c.c).
Suy ra (hai góc tương ứng).
Mà góc AMB và góc AMC là hai góc kề bù nên ta có (tính chất hai góc kề bù).
Do đó .
Suy ra
Từ (chứng minh trên), suy ra (hai góc tương ứng).
Do đó AM là tia phân giác của góc BAC.
Bài 4.25 trang 84 Toán 7 Tập 1: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
Lời giải:
a)
|
GT |
, M là trung điểm BC, . |
|
KL |
cân tại A. |
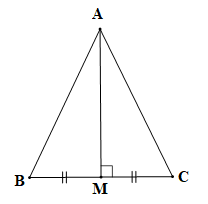
Vì M là trung điểm của BC và (theo giả thiết) nên đường thẳng AM là đường trung trực của đoạn thẳng BC.
Điểm A nằm trên đường trung trực của đoạn thẳng BC nên AB = AC (tính chất đường trung trực của một đoạn thẳng).
Do đó tam giác ABC cân tại A (định nghĩa tam giác cân).
b)
|
GT |
, M là trung điểm BC; AM là tia phân giác của góc BAC. |
|
KL |
cân tại A. |
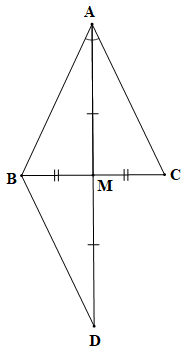
Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
Xét tam giác DBM và tam giác ACM có:
BM = CM (do M là trung điểm của BC);
(hai góc đối đỉnh);
MD = MA (theo cách vẽ).
Vậy (c.g.c).
Suy ra DB = AC (hai cạnh tương ứng) . (1)
Và (hai góc tướng ứng).
Mà (do AM là tia phân giác của góc BAC).
Do đó .
Hay suy ra tam giác ABD cân tại B.
Suy ra AB = DB (định nghĩa tam giác cân). (2)
Từ (1) và (2) suy ra AB = AC.
Do đó tam giác ABC cân tại A (định nghĩa tam giác cân).
Bài 4.26 trang 84 Toán 7 Tập 1: Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45o;
c) Tam giác vuông có một góc nhọn bằng 45o là tam giác vuông cân.
Lời giải:
a)
|
GT |
là tam giác vuông cân;
|
|
KL |
cân tại A. |
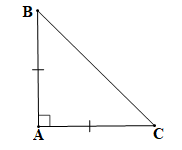
Tam giác ABC vuông tại A nên hai góc nhọn của tam giác phụ nhau suy ra
Khi đó số đo của góc B và góc C sẽ nhỏ hơn 90°.
+) Nếu tam giác ABC cân tại B nên (tính chất tam giác cân).
Mà nên (vô lí vì )
Suy ra tam giác ABC vuông tại A thì không thể cân tại B.
+) Nếu tam giác ABC cân tại C nên (tính chất tam giác cân).
Mà nên (vô lí vì )
Suy ra tam giác ABC vuông tại A thì không thể cân tại C.
Do vậy tam giác ABC vuông tại A và cân tại A.
b)
|
GT |
là tam giác vuông cân. |
|
KL |
Hai góc nhọn bằng 45°. |
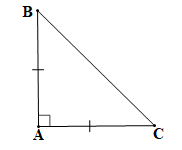
Tam giác ABC vuông cân nên tam giác ABC cân tại đỉnh A (theo câu a).
Suy ra (tính chất tam giác cân).
Mà trong một tam giác vuông, hai góc nhọn phụ nhau nên ta có: .
Do đó
Khi đó
c)
|
GT |
vuông tại A, |
|
KL |
là tam giác vuông cân. |
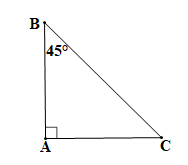
Tam giác ABC vuông tại A (theo giả thiết) nên hai góc nhọn phụ nhau.
Do đó
Suy ra
Khi đó suy ra tam giác ABC cân tại A.
Mà tam giác ABC vuông tại A nên tam giác ABC vuông cân tại A.
Vậy tam giác ABC vuông cân tại A.
Lời giải:
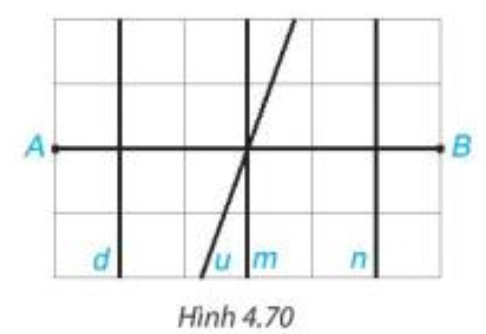
Quan sát hình vẽ ta thấy đường kẻ ngang vuông góc với đường kẻ dọc. Khi đó trong 4 đường thẳng d, u, m, n thì có ba đường thẳng d, m và n vuông góc với đoạn thẳng AB.
Trong hình vẽ, đoạn thẳng AB được chia làm 6 đoạn thẳng bằng nhau.
Do đó trung điểm của AB là điểm nằm trên đoạn thẳng AB và cách A (cách B) 3 đoạn thẳng nhỏ.
Vì vậy chỉ có đường thẳng m thoả mãn điều kiện vuông góc với đoạn thẳng AB và đi qua trung điểm của AB, khi đó đường thẳng m là đường trung trực của đoạn thẳng AB.
Vậy trong các đường thẳng trên hình vẽ, đường thẳng m là đường trung trực của đoạn thẳng AB.
Lời giải:
|
GT |
cân tại A, đường cao AD. |
|
KL |
AD là đường trung trực của BC. |
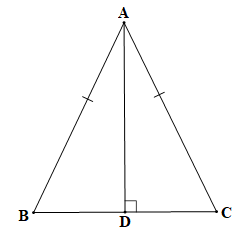
Chứng minh (hình vẽ trên):
Vì AD là đường cao của tam giác ABC nên .
Khi đó tam giác ABD vuông tại D và tam giác ACD vuông tại D.
Xét tam giác ABD (vuông tại D) và tam giác (ACD vuông tại D) ta có:
AB = AC (do tam giác ABC cân tại A);
AD là cạnh chung.
Vậy (cạnh huyền – cạnh góc vuông).
Suy ra DB = DC (hai cạnh tương ứng).
Do đó D là trung điểm của BC.
Khi đó đường thẳng AD vuông góc với đoạn thẳng BC tại trung điểm D của BC nên AD là đường trung trực của BC.
Lý thuyết Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng - Kết nối tri thức
1. Tam giác cân và tính chất
• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
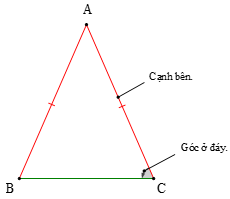
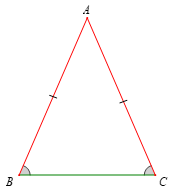
Ví dụ: Trong hình dưới đây, có cạnh AB = AC được gọi là tam giác cân tại đỉnh A, hai cạnh AB và AC là hai cạnh bên, BC là cạnh đáy, và là hai góc ở đáy, là góc ở đỉnh.
• Tính chất:
+ Trong tam giác cân, hai góc ở đáy bằng nhau.
+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.
Ví dụ: Tam giác ABC cân tại A thì =. Ngược lại, tam giác ABC có =thì tam giác ABC cân tại A.
Chú ý:
• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.
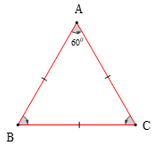
Ví dụ: Tam giác ABC có AB = AC = BC thì tam giác ABC được gọi là tam giác đều. Tam giác ABC đều có = == 60°.
• Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.
• Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.
2. Đường trung trực của một đoạn thẳng
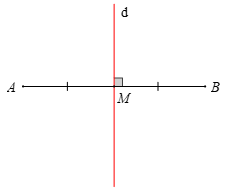
• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Ví dụ: Đường thẳng d vuông góc với đoạn AB tại M và M là trung điểm của AB. Khi đó d được gọi là đường trung trực của đoạn thẳng AB.
• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.
• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
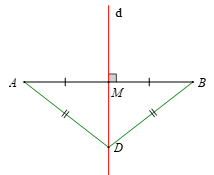
Ví dụ: Đường thẳng d là đường trung trực của đoạn thẳng AB và D ∈ d.
Khi đó DA = DB.
• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.
Chú ý:
• Cách vẽ đường trung trực của đoạn thẳng bằng compa và thước thẳng.
Chẳng hạn: Vẽ đường thẳng d là đường trung trực của đoạn thẳng AB như sau:
+ Vẽ đoạn thẳng AB;
+ Lấy A làm tâm, vẽ cung tròn (bán kính lớn hơn ). Sau đó lấy B làm tâm, vẽ cung tròn cùng bán kính sao cho hai cung này cắt nhau tại hai điểm M và N;
+ Dùng thước thẳng vẽ đường thẳng đi qua M và N. Đường thẳng đó là đường trung trực của đoạn thẳng AB.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Luyện tập chung trang 85, trang 86
Bài tập cuối chương 4 trang 87
Bài 17: Thu thập và phân loại dữ liệu
Xem thêm các chương trình khác:
- Giải sgk Lịch sử 7 – Kết nối tri thức
- Lý thuyết Lịch Sử 7 – Kết nối tri thức
- Giải sbt Lịch sử 7 – Kết nối tri thức
- Giải VTH Lịch sử 7 – Kết nối tri thức
- Soạn văn lớp 7 (hay nhất) – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Soạn văn lớp 7 (ngắn nhất) – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Văn mẫu lớp 7 – Kết nối tri thức
- Giải VTH Ngữ văn lớp 7 – Kết nối tri thức
- Giải sgk Địa Lí 7 – Kết nối tri thức
- Lý thuyết Địa Lí 7 – Kết nối tri thức
- Giải sbt Địa lí 7 – Kết nối tri thức
- Giải VTH Địa lí 7 – Kết nối tri thức
- Giải sgk Tiếng Anh 7 Global Success – Kết nối tri thức
- Giải sbt Tiếng Anh 7 Global Success - Kết nối tri thức
- Bài tập Tiếng Anh 7 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 7 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 7 Global success
- Giải sgk Giáo dục công dân 7 – Kết nối tri thức
- Lý thuyết GDCD 7 – Kết nối tri thức
- Giải sbt Giáo dục công dân 7 – Kết nối tri thức
- Giải vth Giáo dục công dân 7 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 7 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Hoạt động trải nghiệm lớp 7 - KNTT
- Giải sgk Hoạt động trải nghiệm 7 - KNTT
- Giải sgk Công nghệ 7 – Kết nối tri thức
- Lý thuyết Công nghệ 7 – Kết nối tri thức
- Giải sbt Công nghệ 7 – Kết nối tri thức
- Giải VTH Công nghệ 7 – KNTT
- Giải sgk Tin học 7 – Kết nối tri thức
- Lý thuyết Tin học 7 – Kết nối tri thức
- Giải sbt Tin học 7 – Kết nối tri thức
- Giải VTH Tin học 7 – Kết nối tri thức
- Giải sgk Giáo dục thể chất 7 – Kết nối tri thức
- Giải sgk Âm nhạc 7 – Kết nối tri thức