Toán 7 Bài 19 (Kết nối tri thức): Biểu đồ đoạn thẳng

Giải bài tập Toán 7 Bài 19: Biểu đồ đoạn thẳng

Mở đầu

Mở đầu trang 100 Toán 7 Tập 1: Sự thay đổi dân số Việt Nam theo thời gian từ năm 1979 đến 2019, được biểu diễn bằng biểu đồ đoạn thẳng như Hình 5.21.

Qua biểu đồ đoạn thẳng, ta có thể thu nhận được những thông tin gì? Cách vẽ biểu đồ đó như thế nào? Chúng ta cùng tìm hiểu loại biểu đồ này!

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Lời giải:

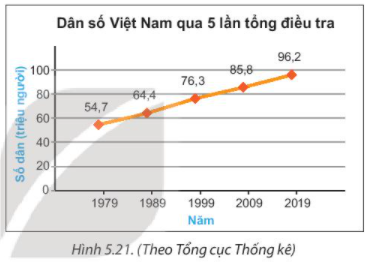
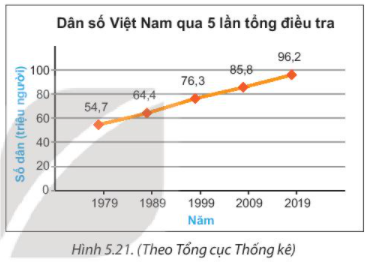
Quan sát biểu đồ đoạn thẳng Hình 5.21 ta có thể xác định được dân số của Việt Nam theo từng năm như sau:

Năm 1979: Dân số Việt Nam là 54,7 triệu người.

Năm 1989: Dân số Việt Nam là 64,4 triệu người.

Năm 1999: Dân số Việt Nam là 76,3 triệu người.

Năm 2009: Dân số Việt Nam là 85,8 triệu người.

Năm 2019: Dân số Việt Nam là 96,2 triệu người.

Để vẽ biểu đồ đoạn thẳng biểu diễn số liệu về dân số Việt Nam qua các năm từ năm 1979 đến năm 2019, ta thực hiện theo các bước sau:

Bước 1. Vẽ trục ngang biểu diễn năm, trục đứng biểu diễn số dân (đơn vị triệu người).

Do số dân cao nhất là 96,2 triệu người và thấp nhất là 54,7 triệu người nên ở trục đứng ta chọn đơn vị là 20 và giá trị lớn nhất là 100.

Bước 2. Với mỗi năm trên trục ngang, số dân của Việt Nam được biểu diễn bởi một điểm.

Số dân năm 1979 được biểu diễn bởi điểm 54,7;

Số dân năm 1989 được biểu diễn bởi điểm 64,4;

Số dân năm 1999 được biểu diễn bởi điểm 76,3;

Số dân năm 2009 được biểu diễn bởi điểm 85,8;

Số dân năm 2019 được biểu diễn bởi điểm 96,5.

Bước 3. Nối các điểm liên tiếp với nhau bằng các đoạn thẳng.

Bước 4. Ghi chú thích cho các trục, điền giá trị tại các điểm và đặt tên cho biểu đồ để hoàn thiện biểu đồ.

1. Giới thiệu về biểu đồ đoạn thẳng

Giải Toán 7 trang 101 Tập 1

Luyện tập 1 trang 101 Toán 7 Tập 1: Biểu đồ Hình 5.23 cho biết thứ hạng của bóng đá nam Việt Nam trên bảng xếp hạng của Liên đoàn Bóng đá thế giới (FIFA) trong các năm từ 2016 đến 2020.

a) Xác định tên biểu đồ, các trục, đơn vị trên các trục.

b) Em hãy cho biết mỗi điểm trên biểu đồ biểu diễn thông tin gì.

Lời giải:

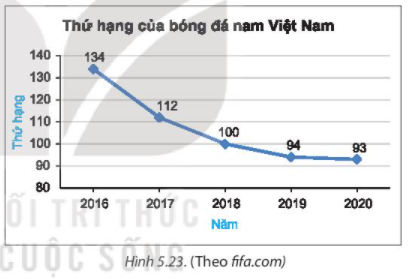
a) Tên biểu đồ: Thứ hạng của bóng đá nam Việt Nam.

Trục ngang là trục biểu diễn thời gian (đơn vị là năm), trục đứng là trục biểu diễn thứ hạng (đơn vị là số thứ tự).

b) Mỗi điểm trên biểu đồ biểu diễn thứ hạng của bóng đá nam Việt Nam so với thế giới qua các năm.

Điểm 134 biểu diễn thứ hạng của bóng đá nam Việt Nam năm 2016;

Điểm 112 biểu diễn thứ hạng của bóng đá nam Việt Nam năm 2017;

Điểm 100 biểu diễn thứ hạng của bóng đá nam Việt Nam năm 2018;

Điểm 94 biểu diễn thứ hạng của bóng đá nam Việt Nam năm 2019;

Điểm 93 biểu diễn thứ hạng của bóng đá nam Việt Nam năm 2020.

2. Đọc và phân tích dữ liệu trong biểu đồ đoạn thẳng

HĐ 1 trang 101 Toán 7 Tập 1: Quan sát biểu đồ (H.5.21).

Em hãy thống kê số dân của Việt Nam từ năm 1979 đến năm 2019 bằng cách hoàn thành bảng sau:

Lời giải:

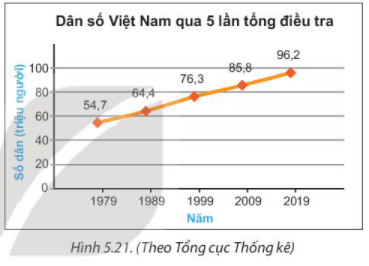
Quan sát biểu đồ Hình 5.21 ta có:

- Số dân của Việt Nam năm 1989 là 64,4 triệu người;

- Số dân của Việt Nam năm 2009 là 85,8 triệu người;

- Số dân của Việt Nam năm 2019 là 96,5 triệu người.

Ta có bảng sau:

HĐ2 trang 101 Toán 7 Tập 1: Quan sát biểu đồ (H.5.21).

Số dân của Việt Nam tăng hay giảm qua các năm từ 1979 đến 2019?

Lời giải:

Quan sát biểu đồ Hình 5.21 ta thấy số dân của Việt Nam tăng qua các năm từ năm 1979 đến năm 2019.

Giải Toán 7 trang 102 Tập 1

Luyện tập 2 trang 102 Toán 7 Tập 1: Biểu đồ Hình 5.25 cho biết số lượt khách quốc tế đến Việt Nam trong những năm gần đây.

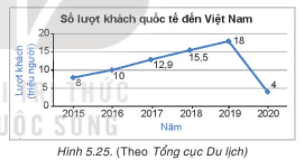
a) Năm 2018 có bao nhiêu lượt khách quốc tế đến Việt Nam?

b) Từ năm 2015 đến năm 2019, số lượt khách quốc tế đến Việt Nam có xu hướng tăng hay giảm?

c) Em có biết vì sao số lượt khách quốc tế đến Việt Nam trong năm 2020 lại giảm mạnh không?

Lời giải:

a) Quan sát biểu đồ Hình 5.25 ta thấy năm 2018 có 15,5 triệu lượt khách quốc tế đến Việt Nam.

b) Quan sát biểu đồ Hình 5.25 ta thấy từ năm 2015 đến năm 2019, số lượt khách quốc tế đến Việt Nam có xu hướng tăng (tăng từ 8 triệu người lên 18 triệu người).

c) Theo em, số lượt khách quốc tế đến Việt Nam trong năm 2020 giảm mạnh do dịch bệnh Covid diễn ra hạn chế di chuyển tránh lây lan cộng đồng gây ảnh hưởng đến ngành du lịch.

Giải Toán 7 trang 103 Tập 1

Luyện tập 3 trang 103 Toán 7 Tập 1: Biểu đồ Hình 5.27 cho biết tỉ lệ học sinh biết bơi của hai tỉnh A, B trong các năm từ 2016 đến 2020.

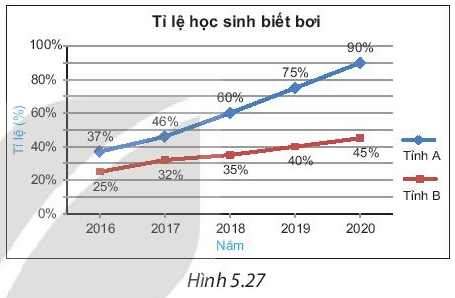
Em có nhận xét gì về tỉ lệ học sinh biết bơi của hai tỉnh A và B từ năm 2016 đến 2020?

Trong giai đoạn này, tỉnh nào có tỉ lệ học sinh biết bơi tăng nhanh hơn?

Lời giải:

Quan sát biểu đồ, ta thấy từ năm 2016 đến năm 2020 thì tỉ lệ học sinh biết bơi của tỉnh A nhiều hơn tỉ lệ học sinh biết bơi của tỉnh B.

Trong giai đoạn này thì tỉ lệ học sinh biết bơi của tỉnh A tăng nhanh hơn tỉ lệ học sinh biết bơi của tỉnh B.

3. Vẽ biểu đồ đoạn thẳng

Thực hành trang 103 Toán 7 Tập 1:

Để vẽ biểu đồ đoạn thẳng biểu diễn số liệu về chiều cao cây đậu trong Bảng 5.1, ta thực hiện theo các bước sau:

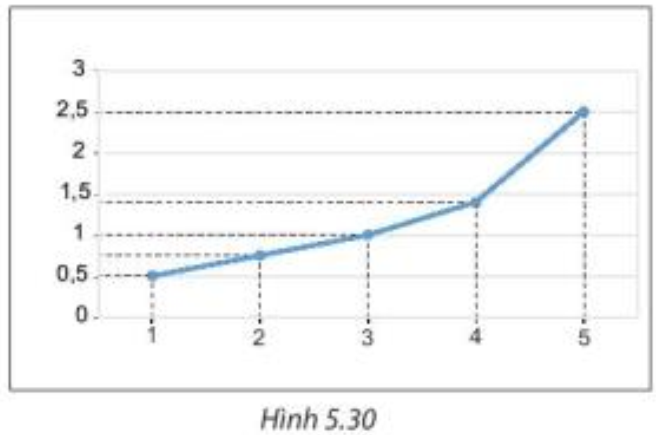
Bước 1. Vẽ trục ngang biểu diễn ngày, trục đứng biểu diễn chiều cao cây đậu.

Do chiều cao lớn nhất là 2,5 cm và thấp nhất là 0,5 cm nên ở trục đứng ta chọn đơn vị là 0,5 và giá trị lớn nhất là 3 (H.5.28).

Bước 2. Với mỗi ngày trên trục ngang, chiều cao của cây đậu tại ngày đó được biểu diễn bởi một điểm (H.5.29).

Bước 3. Nối các điểm liên tiếp với nhau bằng các đoạn thẳng (H.5.30).

Bước 4. Ghi chú thích cho các trục, điền giá trị tại các điểm (nếu cần) và đặt tên cho biểu đồ để hoàn thiện biểu đồ.

Lời giải:

Học sinh thực hiện theo các bước đã hướng dẫn.

Luyện tập 4 trang 102 Toán 7 Tập 1: Bảng thống kê sau đây cho biết thành tích của một vận động viên chạy cự li 1 500 m trong thời gian luyện tập từ tuần 1 đến tuần 7.

Hãy vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu trên.

Lời giải:

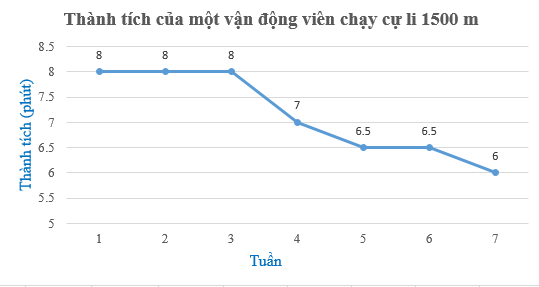
Để vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu về thành tích của vận động viên chạy cự li 1 500 m trong thời gian luyện tập từ tuần 1 đến tuần 7, ta thực hiện theo các bước sau:

Bước 1. Vẽ trục ngang biểu diễn tuần, trục đứng biểu diễn thành tích chạy của vận động viên.

Do thành tích lâu nhất là 8 phút, nhanh nhất là 6 phút và có thành tích 6,5 phút nên ở trục đứng ta chọn đơn vị là 0,5 và giá trị lớn nhất là 8,5.

Bước 2. Với mỗi tuần trên trục ngang, thành tích của vận động viên tại tuần đó được biểu diễn bởi một điểm.

Thành tích của vận động viên tại tuần 1 được biểu diễn bởi điểm 8;

Thành tích của vận động viên tại tuần 2 được biểu diễn bởi điểm 8;

Thành tích của vận động viên tại tuần 3 được biểu diễn bởi điểm 8;

Thành tích của vận động viên tại tuần 4 được biểu diễn bởi điểm 7;

Thành tích của vận động viên tại tuần 5 được biểu diễn bởi điểm 6,5;

Thành tích của vận động viên tại tuần 6 được biểu diễn bởi điểm 6,5;

Thành tích của vận động viên tại tuần 7 được biểu diễn bởi điểm 6.

Bước 3. Nối các điểm liên tiếp với nhau bằng các đoạn thẳng.

Bước 4. Ghi chú thích cho trục ngang và trục đứng, điền giá trị tại các điểm (nếu cần) và đặt tên cho biểu đồ là “Thành tích của một vận động viên chạy cự li 1500 m” để hoàn thiện biểu đồ như dưới đây.

Giải Toán 7 trang 104 Tập 1

Thử thách nhỏ trang 104 Toán 7 Tập 1: Cho hai biểu đồ biểu diễn tuổi thọ trung bình của người Việt Nam qua các năm (H.5.31).

Theo em, để thấy rõ hơn tuổi thọ trung bình của người Việt Nam ngày càng tăng, ta nên dùng biểu đồ nào?

Lời giải:

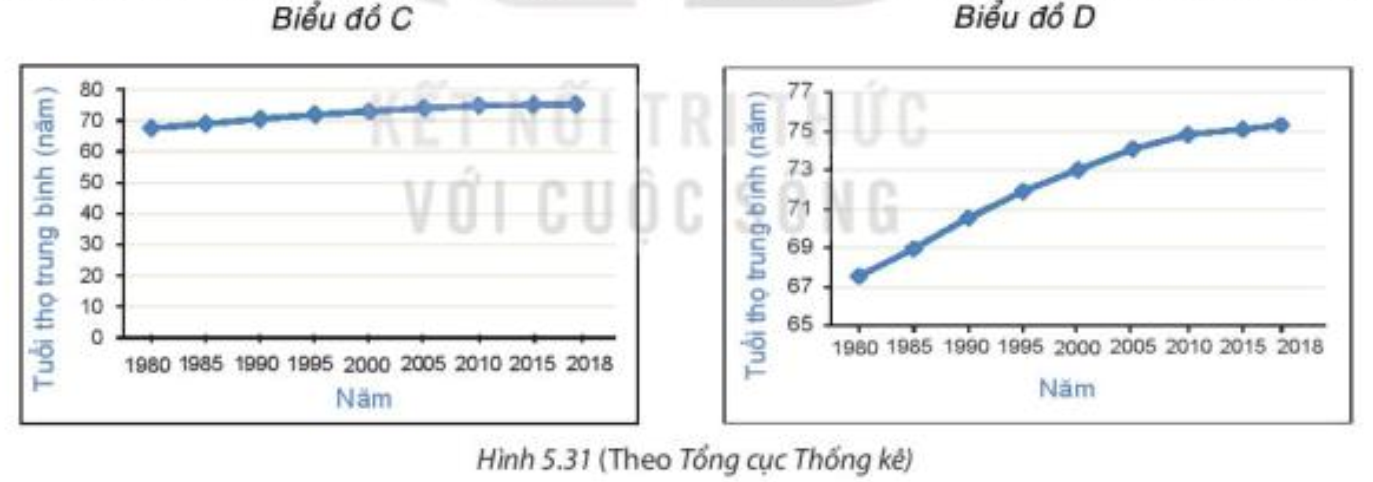
Để thấy rõ hơn tuổi thọ trung bình của người Việt Nam ngày càng tăng thì ta nên sử dụng biểu đồ D do biểu đồ D thể hiện rõ hơn sự thay đổi và xu hướng tăng của tuổi thọ trung bình người Việt Nam (Biểu đồ D thể hiện độ dốc rõ hơn biểu đồ C).

Bài tập

Giải Toán 7 trang 105 Tập 1

Bài 5.10 trang 105 Toán 7 Tập 1: Biểu đồ Hình 5.32 cho biết kỉ lục thế giới về thời gian chạy cự li 100 m trong các năm từ 1912 đến 2009.

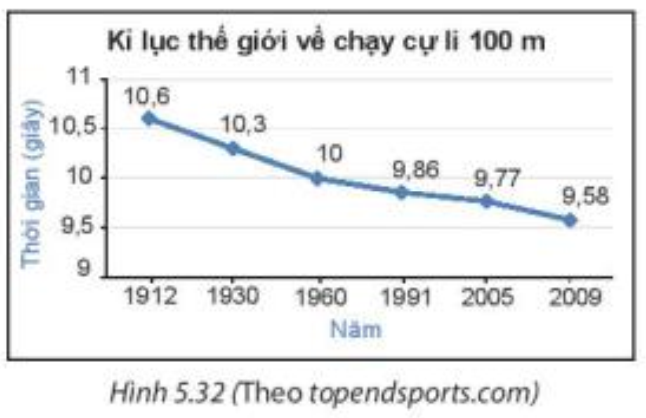
a) Kỷ lục thế giới về chạy cự li 100 m đạt được ở năm 1991 là bao nhiêu giây?

b) Từ năm 1912 đến 2009, kỉ lục thế giới về chạy cự li 100 m đã giảm được bao nhiêu giây?

Lời giải:

a) Quan sát biểu đồ Hình 5.32 ta thấy kỉ lục thế giới về chạy cự li 100 m đạt được ở năm 1991 là 9,86 giây.

b) Kỉ lục thế giới về chạy cự li 100 m đạt được ở năm 1912 là 10,6 giây và ở năm 2009 là 9,58 giây.

Do đó từ năm 1912 đến 2009, kỉ lục thế giới về chạy cự li 100 m đã giảm được số giây là:

10,6 – 9,58 = 1,02 (giây).

Vậy từ năm 1912 đến năm 2009, kỉ lục thế giới về chạy cự li 100 m đã giảm được 1,02 giây.

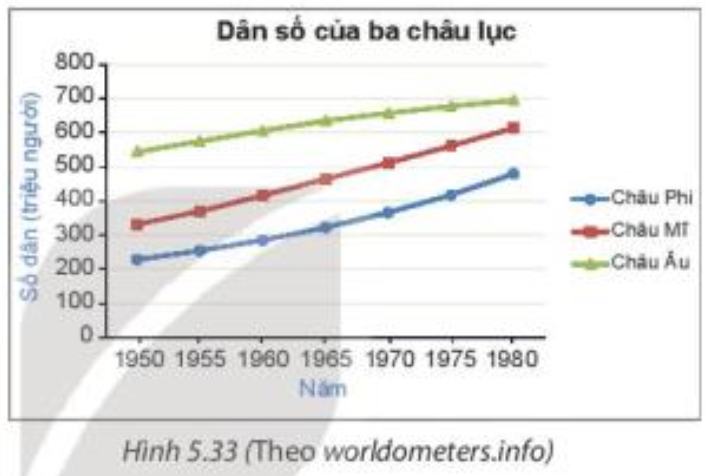
Bài 5.11 trang 105 Toán 7 Tập 1: Biểu đồ Hình 5.33 cho biết số dân của ba châu lục gồm châu Phi, châu Mĩ và châu Âu trong một số năm.

a) Cho biết xu hướng tăng, giảm về số dân của mỗi châu lục theo thời gian.

b) Trong ba châu lục trên, châu lục nào có số dân cao nhất, thấp nhất trong các năm từ 1950 đến 1980?

c) Từ năm 1950 đến 1980, số dân của châu lục nào tăng chậm nhất?

Lời giải:

a) Quan sát biểu đồ Hình 5.33 ta thấy từ năm 1950 đến năm 1980, số dân của cả ba châu lục châu Phi, châu Mĩ, châu Âu đều có xu hướng tăng.

b) Trong ba châu lục, từ năm 1950 đến năm 1980:

- Châu lục có số dân cao nhất là châu Âu;

- Châu lục có số dân thấp nhất là châu Phi.

c) Quan sát Hình 5.33 ta thấy độ dốc của đường thẳng biểu diễn số dân của châu Âu là nhỏ nhất, thể hiện sự tăng chậm nhất.

Vậy số dân của châu Âu tăng chậm nhất.

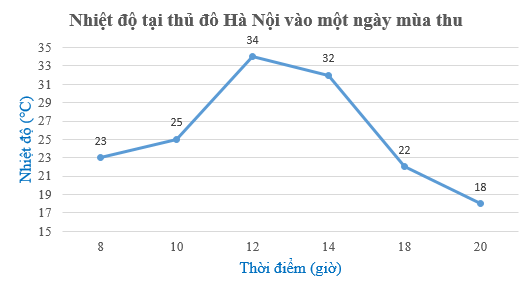
Bài 5.12 trang 105 Toán 7 Tập 1: Bảng sau cho biết nhiệt độ tại thủ đô Hà Nội vào một ngày mùa thu.

Vẽ biểu đồ đoạn thẳng biểu diễn bảng thống kê trên.

Lời giải:

Để vẽ biểu đồ đoạn thẳng biểu diễn bảng số liệu về nhiệt độ tại thủ đô Hà Nội vào một ngày mùa thu, ta thực hiện theo các bước sau:

Bước 1. Vẽ trục ngang biểu diễn thời điểm (đơn vị là giờ), trục đứng biểu diễn nhiệt độ (đơn vị là ^oC).

Do nhiệt độ cao nhất là 34^oC, nhiệt độ thấp nhất là 18^oC nên ở trục đứng ta chọn đơn vị là 2^oC và giá trị lớn nhất là 35^oC.

Bước 2. Với mỗi thời điểm trên trục ngang, nhiệt độ tại từng thời điểm trong ngày được biểu diễn bởi một điểm.

Nhiệt độ tại Hà Nội tại thời điểm 8 giờ được biểu diễn bởi điểm 23;

Nhiệt độ tại Hà Nội tại thời điểm 10 giờ được biểu diễn bởi điểm 25;

Nhiệt độ tại Hà Nội tại thời điểm 12 giờ được biểu diễn bởi điểm 34;

Nhiệt độ tại Hà Nội tại thời điểm 14 giờ được biểu diễn bởi điểm 32;

Nhiệt độ tại Hà Nội tại thời điểm 16 giờ được biểu diễn bởi điểm 26;

Nhiệt độ tại Hà Nội tại thời điểm 18 giờ được biểu diễn bởi điểm 22;

Nhiệt độ tại Hà Nội tại thời điểm 20 giờ được biểu diễn bởi điểm 18;

Bước 3. Nối các điểm liên tiếp với nhau bằng các đoạn thẳng.

Bước 4. Ghi chú thích cho các trục, điền giá trị tại các điểm (nếu cần) và đặt tên “Nhiệt độ tại thủ đô Hà Nội vào một ngày mùa thu” cho biểu đồ để hoàn thiện biểu đồ.

Ta có biểu đồ như dưới đây.

Bài 5.13 trang 105 Toán 7 Tập 1: Số trận thắng của một đội bóng trong 8 năm từ năm 2013 đến năm 2020 được cho như sau:

36 42 15 23 25 35 32 20.

a) Hãy vẽ biểu đồ đoạn thẳng biểu diễn dãy số liệu trên.

b) Cho biết số trận thắng của đội bóng này trong các năm có xu hướng tăng hay giảm?

Lời giải:

a) Để vẽ biểu đồ đoạn thẳng biểu diễn dãy số liệu về số trận thắng của một đội bóng trong 8 năm từ năm 2013 đến năm 2020, ta thực hiện theo các bước sau:

Bước 1. Vẽ trục ngang biểu diễn năm, trục đứng biểu diễn số trận thắng.

Do số trận thắng cao nhất là 42, thấp nhất là 15 nên ở trục đứng ta chọn đơn vị là 2 trận thắng và giá trị lớn nhất là 44.

Bước 2. Với mỗi thời điểm trên trục ngang, số trận thắng tại mỗi năm được biểu diễn bởi một điểm.

Số trận thắng của đội bóng năm 2013 được biểu diễn bởi điểm 36;

Số trận thắng của đội bóng năm 2014 được biểu diễn bởi điểm 42;

Số trận thắng của đội bóng năm 2015 được biểu diễn bởi điểm 15;

Số trận thắng của đội bóng năm 2016 được biểu diễn bởi điểm 23;

Số trận thắng của đội bóng năm 2017 được biểu diễn bởi điểm 25;

Số trận thắng của đội bóng năm 2018 được biểu diễn bởi điểm 35;

Số trận thắng của đội bóng năm 2019 được biểu diễn bởi điểm 32;

Số trận thắng của đội bóng năm 2020 được biểu diễn bởi điểm 20;

Bước 3. Nối các điểm liên tiếp với nhau bằng các đoạn thẳng.

Bước 4. Ghi chú thích cho các trục, điền giá trị tại các điểm (nếu cần) và đặt tên “Số trận thắng của đội bóng từ năm 2013 đến năm 2020” cho biểu đồ để hoàn thiện biểu đồ.

Ta có biểu đồ như sau:

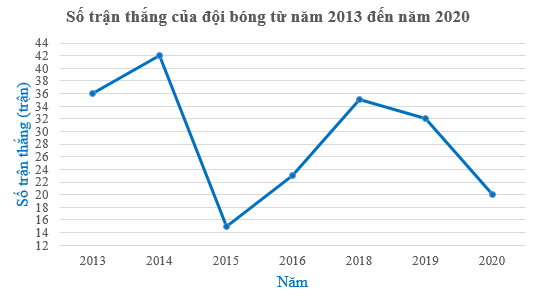
b) Quan sát biểu đồ đoạn thẳng vẽ được ở câu a ta thấy:

- Số trận thắng của đội bóng này từ năm 2013 đến năm 2014 có xu hướng tăng.

- Số trận thắng của đội bóng này từ năm 2014 đến năm 2015 có xu hướng giảm.

- Số trận thắng của đội bóng này từ năm 2015 đến năm 2018 có xu hướng tăng.

- Số trận thắng của đội bóng này từ năm 2018 đến năm 2020 có xu hướng giảm.

Lý thuyết Toán 7 Bài 19: Biểu đồ đoạn thẳng - Kết nối tri thức

1. Giới thiệu biểu đồ đoạn thẳng

• Biểu đồ đoạn thẳng thường được dùng để biểu diễn sự thay đổi của một đại lượng theo thời gian.

• Các thành phần của biểu đồ đoạn thẳng bao gồm:

+ Tiêu đề của biểu đồ thường ở dòng trên cùng.

+ Trục ngang biểu diễn thời gian.

+ Trục đứng biểu diễn đại lượng ta đang quan tâm.

+ Mỗi điểm biểu diễn giá trị của đại lượng tại một thời điểm. Hai điểm liên tiếp được nối với nhau bằng một đoạn thẳng.

Ví dụ:

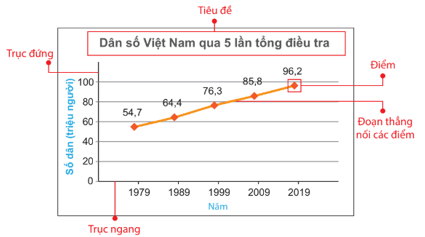
+ Để biểu diễn sự thay đổi của dân số của Việt Nam qua 5 lần tổng điều tra từ năm 1979 đến năm 2019 ta có biểu đồ đoạn thẳng dưới đây:

Mỗi điểm trên biểu đồ cho biết số dân (triệu người) của Việt Nam ở các năm tương ứng. Chẳng hạn, điểm đầu tiên cho biết năm 1979, dân số của Việt Nam là 54,7 triệu người.

Chú ý:

+ Có thể dùng biểu tượng khác như dấu chấm tròn, dấu nhân, … để biểu diễn các điểm.

2. Đọc và phân tích dữ liệu trong biểu đồ đoạn thẳng

• Biểu đồ đoạn thẳng giúp ta dễ dàng nhận ra xu thế của đại lượng ta đang quan tâm theo thời gian.

• Độ dốc của biểu đồ đoạn thẳng cho biết tốc độ tăng của đại lượng được biểu diễn trong biểu đồ.

Ví dụ:

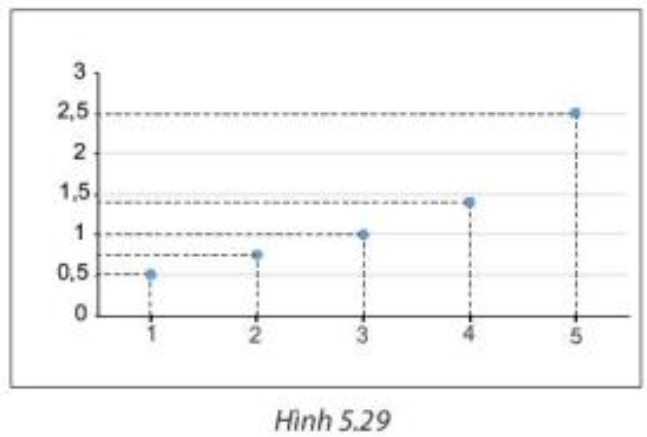
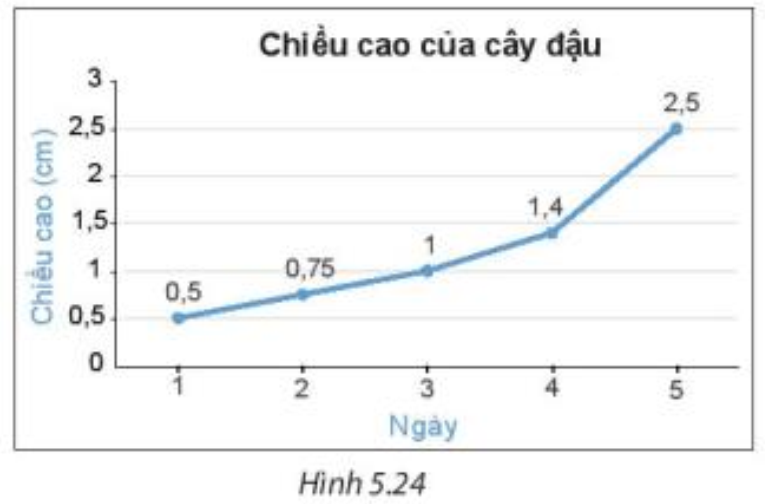
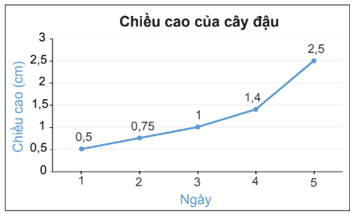
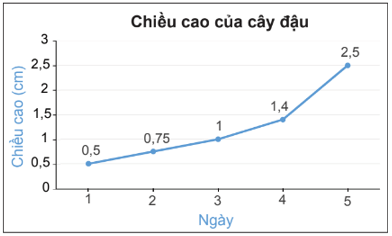
Ta có biểu đồ đoạn thẳng biểu diễn chiều cao của một cây đậu trong 5 ngày dưới đây:

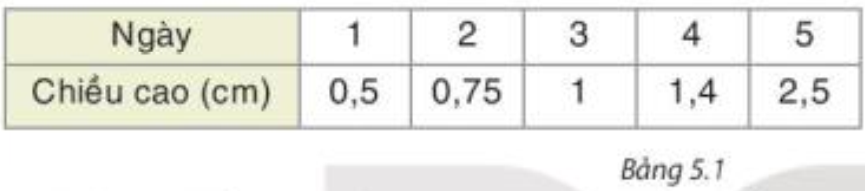
+ Từ biểu đồ ta lập được bảng thống kê về chiều cao của cây đậu:

+ Từ biểu đồ ta thấy đoạn thẳng nối 2 điểm của ngày 4 và 5 có độ dốc cao nhất. Do đó, ngày 5 chiều cao của cây đậu tăng nhiều nhất và tăng 2,5 – 1,4 = 1,1 (cm)

Chú ý:

• Đôi khi người ta biểu diễn nhiều bộ số liệu trên cùng một biểu đồ để so sánh (mỗi đường có chú giải ứng với một bộ số liệu).

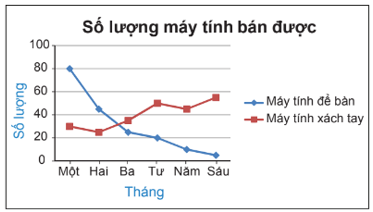
+ Ví dụ: Biểu đồ dưới đây cho biết số lượng máy tính để bàn và máy tính xách tay của một cửa hàng bán được trong 6 tháng đầu năm.

Từ biểu đồ ta thấy được: Trong hai tháng đầu, số lượng máy tính để bàn bán được nhiều hơn. Bốn tháng sau, số lượng máy tính để bàn bán được ngày càng giảm, trong khi số lượng máy tính xách tay bán được có xu hướng tăng. Vì thế, thời gian tới cửa hàng nên nhập nhiều máy tính xách tay.

3. Vẽ biểu đồ đoạn thẳng

• Chẳng hạn, vẽ biểu đồ biểu diễn chiều cao của cây đậu theo bảng thống kê dưới đây, ta làm như sau:

+ Bước 1:Vẽ trục ngang biểu diễn ngày, trục đứng biểu diễn chiều cao cây đậu. Do chiều cao lớn nhất là 2,5 cm và thấp nhất là 0,5 cm nên ở trục đứng ta chọn dơn vị là 0,5 và giá trị lớn nhất là 3.

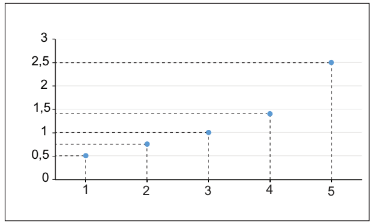
+ Bước 2: Với mỗi ngày trên trục ngang, chiều cao của cây đậu tại ngày đó được biểu diễn bởi một điểm.

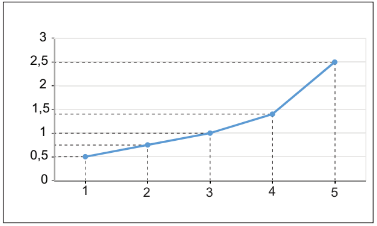
+ Bước 3: Nối các điểm liên tiếp với nhau bằng các đoạn thẳng.

+ Bước 4: Ghi chú thích cho các trục, điền giá trị tại các điểm (nếu cần) và đặt tên cho biểu đồ để hoàn thiện biểu đồ.

Chú ý:

• Độ dốc của biểu đồ phụ thuộc vào việc chọn đơn vị của trục đứng. Khi số liệu lớn trong khi đơn vị độ dài của trục đứng nhỏ thì ta không nên vẽ trục đứng bắt đầu từ 0.

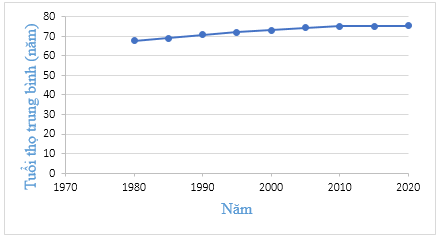
Ví dụ: Hai biểu đồ dưới đây biểu diễn tuổi thọ trung bình của người Việt Nam qua các năm.

Biểu đồ 1

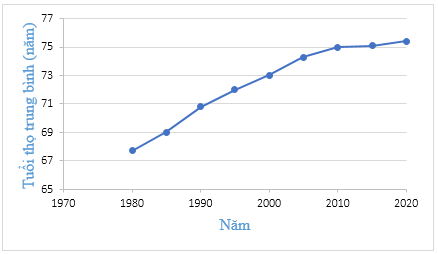
Biểu đồ 2

Biểu đồ 1, trục đứng bắt đầu từ 0, độ dài đơn vị của trục đứng nhỏ. Độ dốc của biểu đồ thấp. Ta không thấy rõ được sự tăng tuổi thọ trung bình qua các năm.

Biểu đồ 2, độ dài đơn vị của trục đứng lớn, độ dốc tăng. Ta thấy rõ được sự tăng tuổi thọ trung bình qua các năm.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 18: Biểu đồ hình quạt tròn

Luyện tập chung

Bài tập cuối chương 5

Vẽ hình đơn giản với phần mềm Geogebra

Dân số và cơ cấu dân số Việt Nam