Toán 7 Bài 3 (Kết nối tri thức): Lũy thừa với số mũ tự nhiên của một số hữu tỉ

Giải bài tập Toán 7 Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ

Video giảng bài tập Toán 7 Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ

Mở đầu

Mở đầu trang 16 Toán 7 Tập 1:

Trái Đất, ngôi nhà chung của tất cả chúng ta có khoảng 71% diện tích bề mặt được bao phủ bởi nước. Nếu gom hết toàn bộ lượng nước trên Trái Đất để đổ đầy vào một bể chứa hình lập phương thì kích thước cạnh của bể phải lên tới 1 111,34 km.

(Theo usgs.gov)

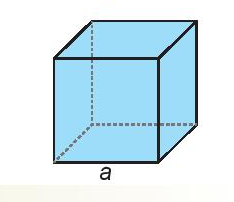
Muốn biết lượng nước trên Trái Đất là khoảng bao nhiêu kilômét khối, ta cần tính

1 111,34 x 1 111,34 x 1 111,34. Biểu thức này có thể viết gọn hơn dưới dạng lũy thừa giống như lũy thừa của một số tự nhiên mà em đã học ở lớp 6.

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Số kilômét khối mà lượng nước trên Trái Đất có là:

1 111,34 x 1 111,34 x 1 111,34 = 1 111,34³.

1. Lũy thừa với số mũ tự nhiên

Giải Toán 7 trang 16 Tập 1

HĐ 1 trang 16 Toán 7 Tập 1:

Viết các tích sau dưới dạng lũy thừa rồi chỉ ra cơ số và số mũ của lũy thừa đó.

a) 2.2.2.2;

b) 5.5.5.

Lời giải:

a) Dạng luỹ thừa của tích 2.2.2.2 được viết là: 2.2.2.2 = 2⁴.

Luỹ thừa trên có cơ số là 2, số mũ là 4.

b) Dạng luỹ thừa của tích 5.5.5 được viết là: 5.5.5 = 5³.

Luỹ thừa trên có cơ số là 5, số mũ là 3.

HĐ 2 trang 16 Toán 7 Tập 1: Thực hiện phép tính:

a) (–2). (–2). (–2);

b) (–0,5). (–0,5);

c) $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.$

Lời giải:

a) Ta có (–2). (–2). (–2) = 4.(–2) = –8.

b) Ta có (–0,5).(–0,5) = 0,5.0,5 = 0,25.

c) Ta có $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{\mathrm{1.1.1.1}}{\mathrm{2.2.2.2}}=\frac{1}{16}.$

HĐ 3 trang 16 Toán 7 Tập 1:

Hãy viết các biểu thức trong HĐ2 dưới dạng lũy thừa tương tự như lũy thừa của số tự nhiên.

Lời giải:

a) Dạng luỹ thừa của tích (–2).(–2).(–2) được viết là: (–2).(–2).(–2) = (–2)³.

b) Dạng luỹ thừa của tích (–0,5).(–0,5) được viết là: (–0,5).(–0,5) = (–0,5)².

c) Dạng luỹ thừa của tích $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}$ được viết là: $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}={\left(\frac{1}{2}\right)}^4.$

Giải Toán 7 trang 17 Tập 1

Luyện tập 1 trang 17 Toán 7 Tập 1: Tính:

a) ${\left(-\frac{4}{5}\right)}^4;$

b) (0,7)³.

Lời giải:

a) Ta có: ${\left(-\frac{4}{5}\right)}^4=\left(-\frac{4}{5}\right).\left(-\frac{4}{5}\right).\left(-\frac{4}{5}\right).\left(-\frac{4}{5}\right)$

$=\frac{-4}{5}.\frac{-4}{5}.\frac{-4}{5}.\frac{-4}{5}$$=\frac{\left(-4\right).\left(-4\right).\left(-4\right).\left(-4\right)}{\mathrm{5.5.5.5}}=\frac{16.16}{25.25}=\frac{256}{625}.$

b) Ta có: (0,7)³ = ${\left(\frac{7}{10}\right)}^3=\frac{7}{10}.\frac{7}{10}.\frac{7}{10}=\frac{\mathrm{7.7.7}}{\mathrm{10.10.10}}=\frac{343}{1000}=0,343.$

Luyện tập 2 trang 17 Toán 7 Tập 1: Tính:

a) ${\left(\frac{2}{3}\right)}^{10}{.3}^{10};$

b) (–125)³ : 25³;

c) (0,08)³.10³.

Lời giải:

a) Áp dụng công thức luỹ thừa của một tích ta có: ${\left(\frac{2}{3}\right)}^{10}{.3}^{10}={\left(\frac{2}{3}.3\right)}^{10}=2^{10}.$

b) Áp dụng công thức luỹ thừa của một thương ta có:

(–125)³ : 25³ = $\frac{{\left(-125\right)}^3}{{25}^3}={\left(\frac{-125}{25}\right)}^3$ = (–5)³ = –125.

c) Áp dụng công thức luỹ thừa của một tích ta có:

(0,08)3.103 = (0,08 . 10)3 = (0,8)3 = 0,512.

Vận dụng trang 17 Toán 7 Tập 1:

Viết công thức tính thể tích của hình lập phương cạnh a dưới dạng lũy thừa. Từ đó viết biểu thức lũy thừa để tính toàn bộ lượng nước trên Trái Đất trong bài toán mở đầu (đơn vị kilômét khối).

Lời giải:

Công thức tính thể tích của hình lập phương cạnh a dưới dạng luỹ thừa là: a.a.a = a³.

Biểu thức luỹ thừa tính toàn bộ lượng nước trên Trái Đất đổ đầy vào bể chứa hình lập phương kích thước cạnh a = 1 111,34 kilômét là: 1 111,34³ (kilômét khối).

Vậy lượng nước trên Trái Đất là 1 111,34³ kilômét khối.

2. Nhân và chia hai lũy thừa cùng cơ số

HĐ 4 trang 17 Toán 7 Tập 1: Tính và so sánh:

a) (–3)².(–3)⁴ và (–3)⁶;

b) 0,6³ : 0,6² và 0,6.

Lời giải:

a) Ta có (–3)².(–3)⁴ = (–3). (–3). (–3). (–3). (–3). (–3) = (–3)⁶.

Vậy (–3)².(–3)⁴ = (–3)⁶.

b) 0,6³ : 0,6² $=\frac{\left(0,6\right).\left(0,6\right).\left(0,6\right)}{\left(0,6\right).\left(0,6\right)}=0,6.$

Vậy 0,6³ : 0,6² = 0,6.

Giải Toán 7 trang 18 Tập 1

Luyện tập 3 trang 18 Toán 7 Tập 1:

Viết kết quả của các phép tính sau dưới dạng lũy thừa.

a) (–2)³.( –2)⁴;

b) (0,25)⁷ : (0,25)³.

Lời giải:

a) Dạng luỹ thừa của phép tính (–2)³.( –2)⁴ là: (–2)³.( –2)⁴ = (–2)³⁺⁴ = (–2)⁷.

b) Dạng luỹ thừa của phép tính (0,25)⁷ : (0,25)³ là: (0,25)⁷ : (0,25)³ = (0,25)^{7 – 3} = (0,25)⁴.

3. Lũy thừa của lũy thừa

HĐ 5 trang 18 Toán 7 Tập 1:

Viết số ${\left(2^2\right)}^3$ dưới dạng lũy thừa cơ số 2 và số ${\left[{\left(-3\right)}^2\right]}^2$ dưới dạng lũy thừa cơ số –3.

Lời giải:

Số ${\left(2^2\right)}^3$ được viết dưới dạng lũy thừa cơ số 2 như sau:

${\left(2^2\right)}^3$ = 2². 2². 2² = 2²⁺²⁺² = 2⁶.

Số ${\left[{\left(-3\right)}^2\right]}^2$ được viết dưới dạng lũy thừa cơ số –3 như sau:

${\left[{\left(-3\right)}^2\right]}^2$ = (–3)². (–3)² = (–3)²⁺² = (–3)⁴.

Luyện tập 4 trang 18 Toán 7 Tập 1:

Viết các số ${\left(\frac{1}{4}\right)}^8;{\left(\frac{1}{8}\right)}^3$ dưới dạng lũy thừa cơ số $\frac{1}{2}$

Lời giải:

Các số ${\left(\frac{1}{4}\right)}^8;{\left(\frac{1}{8}\right)}^3$ được viết dưới dạng lũy thừa cơ số $\frac{1}{2}$ như sau:

${\left(\frac{1}{4}\right)}^8={\left(\frac{1.1}{2.2}\right)}^8={\left(\frac{1}{2}.\frac{1}{2}\right)}^8={\left[{\left(\frac{1}{2}\right)}^2\right]}^8={\left(\frac{1}{2}\right)}^{2.8}={\left(\frac{1}{2}\right)}^{16}.$

${\left(\frac{1}{8}\right)}^3={\left(\frac{1.1}{2.4}\right)}^3={\left(\frac{\mathrm{1.1.1}}{\mathrm{2.2.2}}\right)}^3={\left(\frac{1^3}{2^3}\right)}^3={\left[{\left(\frac{1}{2}\right)}^3\right]}^3={\left(\frac{1}{2}\right)}^{3.3}={\left(\frac{1}{2}\right)}^9.$

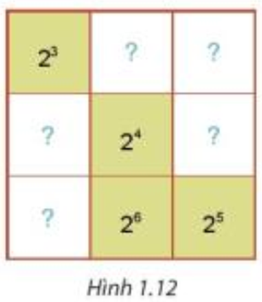
Thử thách nhỏ trang 18 Toán 7 Tập 1:

Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết tích các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.

Lời giải:

Đặt các ô lần lượt là a, b, c, d, e như hình sau:

Theo đề bài, tích các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo là bằng nhau nên tích các lũy thừa trên mỗi hàng, mỗi cột, mỗi đường chéo đều có giá trị bằng tích của đường chéo chứa các ô số đã có sẵn là: 2³.2⁴.2⁵ = 2³⁺⁴⁺⁵ = 2¹².

+) Tích các số của cột 2 là: a.2⁴.2⁶ = a.2¹⁰ có giá trị bằng 2¹² nên ta có a.2¹⁰ = 2¹².

Suy ra a = 2¹² : 2¹⁰ = 2^{12 – 10} = 2².

+) Tích các số của hàng 1 là: 2³.a.b hay 2³.2².b = 2³⁺².b = 2⁵.b có giá trị bằng 2¹² nên ta có 2⁵.b = 2¹².

Suy ra b = 2¹² : 2⁵ = 2^{12 – 5} = 2⁷.

+) Tích các số của hàng 3 là: e.2⁶.2⁵ = e.2¹¹ có giá trị bằng 2¹² nên ta có e.2¹¹ = 2¹²

Suy ra e = 2¹² : 2¹¹ = 2^{12 – 11} = 2¹.

+) Tích các số của cột 1 là: 2³.c.e hay 2³.c.2¹ = c.2³⁺¹ = c.2⁴ có giá trị bằng 2¹² nên ta có c.2⁴ = 2¹².

Suy ra c = 2¹² : 2⁴ = 2^{12 – 4} = 2⁸.

+) Tích các số của hàng 2 là: c.2⁴.d hay 2⁸.2⁴.d = 2⁸⁺⁴.d = 2¹².d có giá trị bằng 2¹² nên ta có 2¹².d = 2¹².

Suy ra d = 2¹² : 2¹² = 2^{12 – 12} = 2⁰.

Ta có bảng như sau:

Bài tập

Bài 1.18 trang 18 Toán 7 Tập 1: Viết các số 125; 3 125 dưới dạng lũy thừa của 5.

Lời giải:

Ta có: 125 = 5.25 = 5.5.5 = 5³.

Vậy số 125 được viết dưới dạng luỹ thừa của 5 là 5³.

Ta có: 3 125 = 5.625 = 5.5.125 = 5².5³ = 5²⁺³ = 5⁵.

Vậy số 3 125 được viết dưới dạng luỹ thừa của 5 là 5⁵.

Bài 1.19 trang 18 Toán 7 Tập 1: Viết các số ${\left(\frac{1}{9}\right)}^5;{\left(\frac{1}{27}\right)}^7$ dưới dạng lũy thừa cơ số $\frac{1}{3}$

Lời giải:

Có: ${\left(\frac{1}{9}\right)}^5={\left(\frac{1.1}{3.3}\right)}^5={\left(\frac{1^2}{3^2}\right)}^5={\left[{\left(\frac{1}{3}\right)}^2\right]}^5={\left(\frac{1}{3}\right)}^{2.5}={\left(\frac{1}{3}\right)}^{10}.$

Vậy số ${\left(\frac{1}{9}\right)}^5$ được viết dưới dạng luỹ thừa cơ số $\frac{1}{3}$ là ${\left(\frac{1}{3}\right)}^{10}.$

Có: ${\left(\frac{1}{27}\right)}^7={\left(\frac{\mathrm{1.1.1}}{\mathrm{3.3.3}}\right)}^7={\left(\frac{1^3}{3^3}\right)}^7={\left[{\left(\frac{1}{3}\right)}^3\right]}^7={\left(\frac{1}{3}\right)}^{3.7}={\left(\frac{1}{3}\right)}^{21}.$

Vậy số ${\left(\frac{1}{27}\right)}^7$ được viết dưới dạng luỹ thừa cơ số $\frac{1}{3}$ là ${\left(\frac{1}{3}\right)}^{21}.$

Giải Toán 7 trang 19 Tập 1

Bài 1.21 trang 19 Toán 7 Tập 1: Không sử dụng máy tính, hãy tính:

a) (–3)⁸, biết (–3)⁷ = –2 187;

b) ${\left(-\frac{2}{3}\right)}^{12},$ biết ${\left(-\frac{2}{3}\right)}^{11}=\frac{-2 048}{177 147}.$

Lời giải:

a) Ta có (–3)⁸ = (–3)⁷⁺¹ = (–3)⁷. (–3)

Mà (–3)⁷ = –2 187 nên ta có (–3)⁷. (–3) = (–2 187). (–3) = 6 561.

Vậy (–3)⁸ = 6 561;

b) Ta có ${\left(-\frac{2}{3}\right)}^{12}={\left(-\frac{2}{3}\right)}^{11+1}={\left(-\frac{2}{3}\right)}^{11}.\left(-\frac{2}{3}\right)$

Mà ${\left(-\frac{2}{3}\right)}^{11}=\frac{-2 048}{177 147}$ nên ta có ${\left(-\frac{2}{3}\right)}^{11}.\left(-\frac{2}{3}\right)=\frac{-2 048}{177 147}.\frac{-2}{3}=\frac{\left(-2 048\right).\left(-2\right)}{177 147.3}=\frac{4 096}{531 441}.$

Vậy ${\left(-\frac{2}{3}\right)}^{12}=\frac{4 096}{531 441}.$

Bài 1.22 trang 19 Toán 7 Tập 1: Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ.

a) 15⁸.2⁴;

b) 27⁵ : 32³.

Lời giải:

a) 15⁸.2⁴ = 15^2.4.2⁴ = (15²)⁴.2⁴ = 225⁴.2⁴ = (225.2)⁴ = 450⁴.

Vậy 15⁸.2⁴ = 450⁴.

b) 27⁵ : 32³ $=\frac{{27}^5}{{32}^3}=\frac{{\left(\mathrm{3.3.3}\right)}^5}{{\left(\mathrm{2.2.2.2.2}\right)}^3}=\frac{{\left(3^3\right)}^5}{{\left(2^5\right)}^3}=\frac{3^{15}}{2^{15}}={\left(\frac{3}{2}\right)}^{15}.$

Vậy 27⁵ : 32³ = ${\left(\frac{3}{2}\right)}^{15}.$

Bài 1.23 trang 19 Toán 7 Tập 1: Tính:

a) ${\left(1+\frac{1}{2}-\frac{1}{4}\right)}^2.\left(2+\frac{3}{7}\right);$

b) $4:{\left(\frac{1}{2}-\frac{1}{3}\right)}^3.$

Lời giải:

a) Ta có:

${\left(1+\frac{1}{2}-\frac{1}{4}\right)}^2.\left(2+\frac{3}{7}\right)$

$={\left(\frac{2}{2}+\frac{1}{2}-\frac{1}{4}\right)}^2.\left(\frac{14}{7}+\frac{3}{7}\right)$

$={\left(\frac{3}{2}-\frac{1}{4}\right)}^2.\left(\frac{14+3}{7}\right)$

$={\left(\frac{6}{4}-\frac{1}{4}\right)}^2.\frac{17}{7}$

$={\left(\frac{5}{4}\right)}^2.\frac{17}{7}$

$=\frac{5^2}{4^2}.\frac{17}{7}$

$=\frac{25.17}{16.7}$

$=\frac{425}{112}.$

b) Ta có:

$4:{\left(\frac{1}{2}-\frac{1}{3}\right)}^3$

$=4:{\left(\frac{3}{6}-\frac{2}{6}\right)}^3$

$=4:{\left(\frac{1}{6}\right)}^3$

$=4:\frac{1^3}{6^3}$

= 4.6³

= 4.216

= 864.

Bài 1.24 trang 19 Toán 7 Tập 1: Khoảng cách từ Trái Đất đến Mặt Trời bằng khoảng 1,5.10⁸ km. Khoảng cách từ Mộc tinh đến Mặt Trời khoảng 7,78.10⁸ km. Hỏi khoảng cách từ Mộc tinh đến Mặt Trời gấp khoảng bao nhiêu lần khoảng cách từ Trái Đất đến Mặt Trời?

(Theo solarsystem.nasa.gov)

Lời giải:

Khoảng cách từ Mộc tinh đến Mặt Trời gấp số lần khoảng cách từ Trái Đất đến Mặt Trời là:

(7,78.10⁸ ) : (1,5.10⁸) $=\frac{7,{78.10}^8}{1,{5.10}^8}=\frac{7,78}{1,5}=\frac{7,78.100}{1,5.100}=\frac{778}{150}=\frac{389}{75}$ (lần).

Vậy khoảng cách từ Mộc tinh đến Mặt Trời gấp $\frac{389}{75}$ lần khoảng cách từ Trái Đất đến Mặt Trời.

Bài 1.25 trang 19 Toán 7 Tập 1: Bảng thống kê dưới đây cho biết số lượng khách quốc tế đến thăm Việt Nam trong năm 2019.

(Theo Viện Nghiên cứu Phát triển Du lịch)

Em hãy sắp xếp tên các quốc gia theo thứ tự số lượng khách đến thăm Việt Nam từ nhỏ đến lớn.

Lời giải:

Ta có: 4,3.10⁶ = 4,3.10²⁺⁴ = 4,3.10².10⁴ = 4,3.100.10⁴ = 430.10⁴;

7,4.10⁵ = 7,4.10¹⁺⁴ = 7,4.10.10⁴ = 74.10⁴.

2,9.10⁵ = 2,9.10¹⁺⁴ = 2,9.10.10⁴ = 29.10⁴.

Do 7 < 29 < 74 < 430 nên 7.10⁴ < 29.10⁴ < 74.10⁴ < 430.10⁴.

Suy ra 7.10⁴ < 2,9.10⁵ < 7,4.10⁵ < 4,3.10⁶.

Vậy các quốc gia sắp xếp theo thứ tự số lượng khách đến thăm Việt Nam từ nhỏ đến lớn là: Ý, Pháp, Hoa Kì, Hàn Quốc.

Lý thuyết Toán 7 Bài 3. Lũy thừa với số mũ tự nhiên của một số hữu tỉ - Kết nối tri thức

1. Lũy thừa với số mũ tự nhiên

• Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1).

${\mathrm{x}}^{\mathrm{n}}=\underset{\mathrm{n} \mathrm{thừa} \mathrm{số}}{\underbrace{\mathrm{x}\cdot \mathrm{x}\cdot \mathrm{x}\cdot ...\cdot \mathrm{x}}}$ (x $\in \mathrm{\mathbb{Q}}$, n $\in \mathrm{\mathbb{N}}$, n >1)

xⁿ đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.

x gọi là cơ số, n gọi là số mũ.

Quy ước: x⁰ = 1 (x ≠ 0); x¹ = x.

Ví dụ:

+ 5³ đọc là 5 mũ 3 hoặc 5 lũy thừa 3 hoặc lũy thừa bậc 3 của 5.

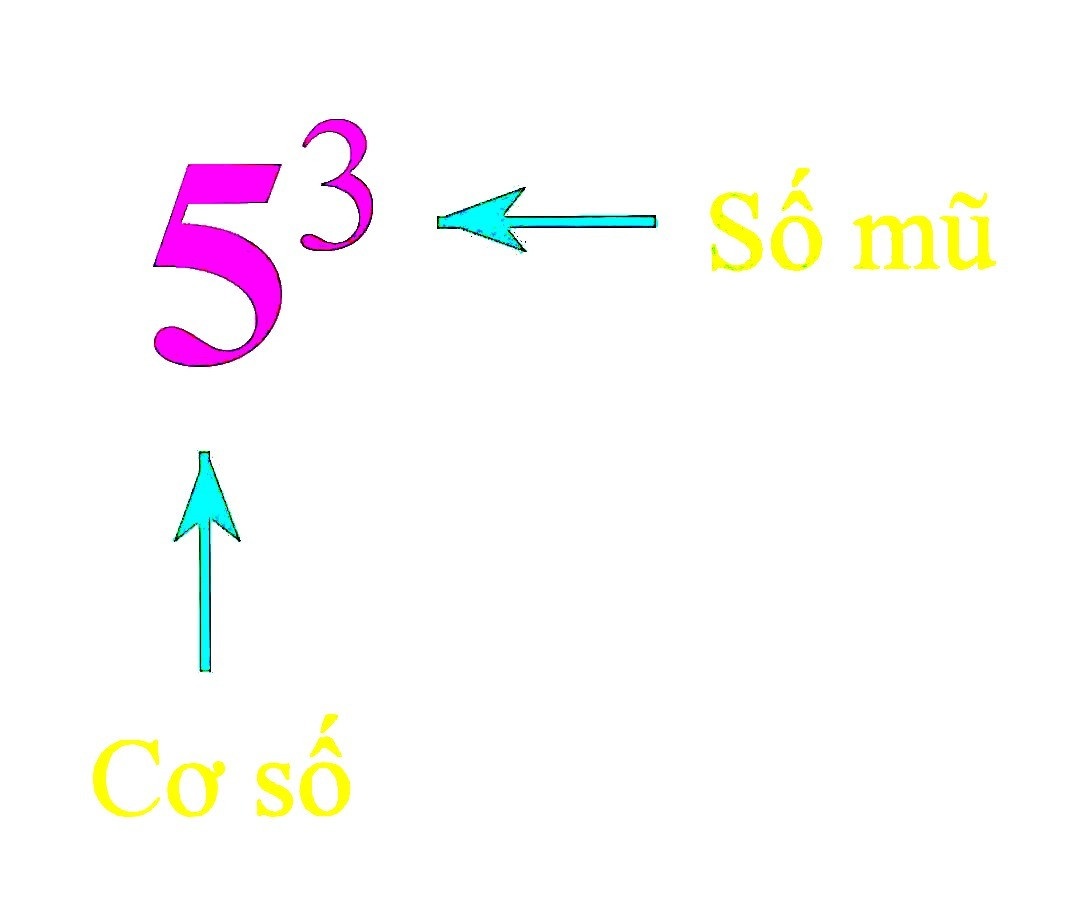
+ Tính ${\left(\frac{-1}{3}\right)}^4$

${\left(\frac{-1}{3}\right)}^4=\frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}=\frac{\left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)}{3\cdot 3\cdot 3\cdot 3}=\frac{1}{81}$

+ Tính và so sánh: $\frac{{12}^2}{6^2}$ và ${\left(-\frac{12}{6}\right)}^2$

$\frac{{12}^2}{6^2}=\frac{144}{36}=4$ và ${\left(-\frac{12}{6}\right)}^2={\left(-2\right)}^2=4$ nên $\frac{{12}^2}{6^2}={\left(-\frac{12}{6}\right)}^2$

Chú ý:

• Lũy thừa của một tích bằng tích các lũy thừa; lũy thừa của một thương bằng thương các lũy thừa.

${\left(\mathrm{x}\cdot \mathrm{y}\right)}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{n}}\cdot {\mathrm{y}}^{\mathrm{n}}$; ${\left(\frac{\mathrm{x}}{\mathrm{y}}\right)}^{\mathrm{n}}=\frac{{\mathrm{x}}^{\mathrm{n}}}{{\mathrm{y}}^{\mathrm{n}}}$ (y ≠ 0).

Ví dụ:

${\left(\frac{3}{4}\right)}^{15}.4^{15}={\left(\frac{3}{4}.4\right)}^{15}=3^{15}$;

25³ : 5³ = ${\left(\frac{25}{5}\right)}^3=5^3=125$.

2. Nhân và chia hai lũy thừa cùng cơ số

• Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

${\mathrm{x}}^{\mathrm{m}}\cdot {\mathrm{x}}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}+\mathrm{n}}$

• Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa chia.

${\mathrm{x}}^{\mathrm{m}}:{\mathrm{x}}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}-\mathrm{n}}$ (x ≠ 0, m ≥ n)

Ví dụ: Tính:

a) ${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5$;

b) Tính ${\left(-9\right)}^5:{\left(-9\right)}^4$.

Hướng dẫn giải

a) ${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5={\left(\frac{2}{3}\right)}^{2+5}={\left(\frac{2}{3}\right)}^7=\frac{128}{2187}$;

b) ${\left(-9\right)}^5:{\left(-9\right)}^4={\left(-9\right)}^{5-4}={\left(-9\right)}^1=-9$.

3. Lũy thừa của lũy thừa

• Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.

${\left({\mathrm{x}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}\cdot \mathrm{n}}$

Ví dụ: Tính ${\left[{\left(-3\right)}^5\right]}^7$

Ta có: ${\left[{\left(-3\right)}^5\right]}^7={\left(-3\right)}^{5\cdot 7}={\left(-3\right)}^{35}$.

Mở rộng

• Lũy thừa với số mũ nguyên âm của một số khác 0.

${\mathrm{x}}^{-\mathrm{n}}=\frac{1}{{\mathrm{x}}^{\mathrm{n}}}$ với n là số nguyên dương, x ≠ 0.

Ví dụ: $\frac{1}{100}=\frac{1}{{10}^2}={10}^{-2}$

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

Luyện tập chung trang 23, 24

Bài tập cuối chương 1 sgk trang 25

Bài 5: Làm quen với số thập phân vô hạn tuần hoàn

Bài 6: Số vô tỉ. Căn bậc hai số học

Xem thêm tài liệu Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ