Toán 7 Bài 12 (Kết nối tri thức): Tổng các góc trong một tam giác

Giải bài tập Toán 7 Bài 12: Tổng các góc trong một tam giác

Video giải bài tập Toán 7 Bài 12: Tổng các góc trong một tam giác

Mở đầu

Mở đầu trang 60 Toán 7 Tập 1: Người ta có thể xếp các viên gạch hình tam giác giống hệt nhau để trang trí như Hình 4.1. Em có nhận xét gì về ba góc tại mỗi đỉnh chung của ba tam giác? Từ đó em rút ra kết luận gì về vị trí của ba điểm A, B, C?

Lời giải:

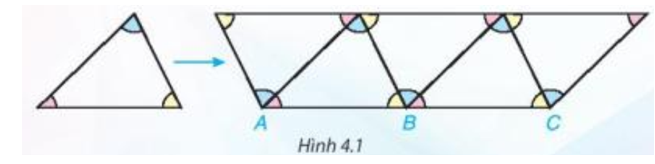
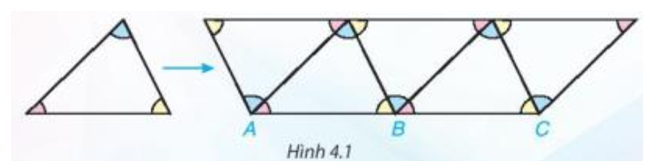
Nhận xét: Khi xếp các viên gạch hình tam giác giống hệt nhau để trang trí như Hình 4.1 ta thấy ba góc tại mỗi đỉnh chung của ba tam giác (như trên hình vẽ ba góc tại đỉnh B) có tổng số đo bằng 180°.

Kết luận: ba điểm A, B, C thẳng hàng.

Tổng các góc trong một tam giác

Giải Toán 7 trang 60 Tập 1

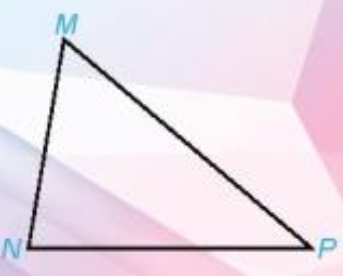
HĐ 1 trang 60 Toán 7 Tập 1: Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó.

- Tổng số đo ba góc của tam giác MNP bằng bao nhiêu?

- So sánh kết quả của em với các bạn và rút ra nhận xét.

Lời giải:

a) Tổng số đo ba góc của tam giác MNP bằng 180°.

b) Kết quả của em giống kết quả của các bạn khác.

Nhận xét: Tổng số đo ba góc của tam giác bằng 180°.

Giải Toán 7 trang 61 Tập 1

HĐ 2 trang 61 Toán 7 Tập 1: Cắt một hình tam giác bằng giấy bất kì (H.4.2a). Đánh dấu ba góc là x, y, z. Cắt hai góc y, z và ghép lên góc x như Hình 4.2b. Từ đó, em hãy dự đoán tổng số đo các góc x, y, z của tam giác ban đầu.

Lời giải:

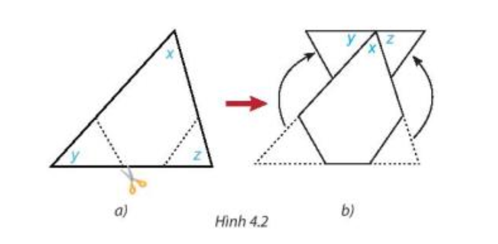
Sau khi cắt ghép ta được Hình 4.2b, tại điểm chung gốc của 3 góc x, y, z có tổng số đo ba góc bằng 180° nên ta dự đoán tổng số đo các góc x, y, z của tam giác ban đầu bằng 180°.

Câu hỏi trang 61 Toán 7 Tập 1: Trở lại tình huống mở đầu, tổng ba góc tại mỗi đỉnh chung của ba tam giác (chẳng hạn tại B trong Hình 4.1) bằng bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không?

Lời giải:

Trong hình vẽ trên, tổng số đo ba góc tại đỉnh chung B của ba tam giác bằng 180°.

Khi đó ba điểm A, B, C thẳng hàng.

Giải Toán 7 trang 62 Tập 1

Luyện tập trang 62 Toán 7 Tập 1: Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.

Lời giải:

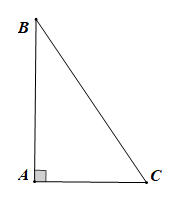
Chứng minh (Hình vẽ trên):

Theo giả thiết tam giác ABC vuông tại A nên $\widehat{A}=90°.$

Trong tam giác ABC ta có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (Định lí tổng ba góc trong một tam giác).

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}=180°-90°=90°.$

Vậy $\widehat{B}+\widehat{C}=90°.$

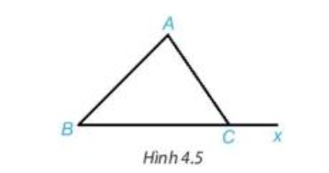
Vận dụng trang 62 Toán 7 Tập 1: Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5).

Chứng minh rằng $\widehat{ACx}=\widehat{BAC}+\widehat{CBA}.$

Lời giải:

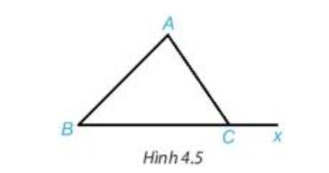
Chứng minh (Hình vẽ trên):

Theo giả thiết Cx là tia đối của tia CB nên hai góc ACB và Acx là hai góc kề bù, hay $\widehat{ACB}+\widehat{ACx}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{ACx}=180°-\widehat{ACB}$ (1).

Trong tam giác ABC ta có $\widehat{BAC}+\widehat{ACB}+\widehat{CBA}=180°$ (Định lí tổng ba góc trong một tam giác).

Suy ra $\widehat{BAC}+\widehat{CBA}=180°-\widehat{ACB}$ (2).

Từ (1) và (2) ta có $\widehat{ACx}=\widehat{BAC}+\widehat{CBA}\left(=180°-\widehat{ACB}\right)$.

Vậy $\widehat{ACx}=\widehat{BAC}+\widehat{CBA}.$

Bài tập

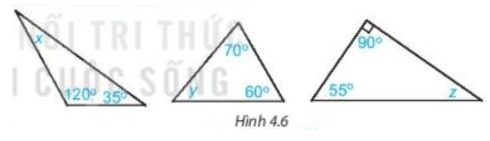
Bài 4.1 trang 62 Toán 7 Tập 1: Tính số đo các góc x, y, z trong Hình 4.6.

Lời giải:

+)

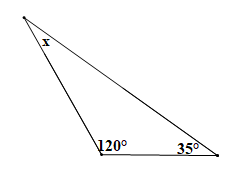
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác trên hình vẽ ta có:

x + 120° + 35° = 180° suy ra x = 180° – 120° – 35° = 25°.

Vậy x = 25°.

+)

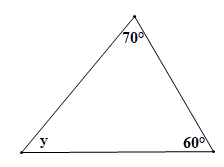
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác trên hình vẽ ta có:

y + 60° + 70° = 180° suy ra y = 180° – 60° – 70° = 50°.

Vậy y = 50°.

+)

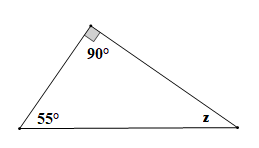
Tam giác trong hình vẽ là tam giác có một góc có số đo bằng 90° nên là tam giác vuông, do đó hai góc nhọn phụ nhau.

Suy ra z + 55° = 90°

z = 90° – 55°

z = 35°.

Vậy z = 35°.

Bài 4.2 trang 62 Toán 7 Tập 1: Trong các tam giác (H.4.7), tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù?

Lời giải:

+)

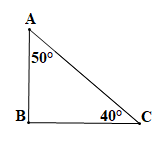
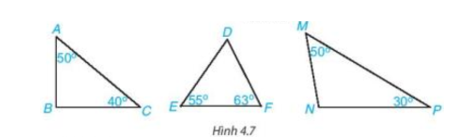
Trên hình vẽ, tam giác ABC có $\widehat{A}=50°,\widehat{C}=40°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{A}+\widehat{B}+\widehat{C}=180°$.

Suy ra $\widehat{B}=180°-\widehat{A}-\widehat{C}$

$\widehat{B}=180°-50°-40°$

$\widehat{B}=90°$

Ta thấy trong tam giác ABC có $\widehat{B}=90°$ là một góc vuông nên tam giác ABC là tam giác vuông tại B.

Vậy tam giác ABC là tam giác vuông tại B.

+)

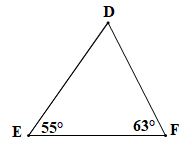
Trên hình vẽ, tam giác DEF có $\widehat{E}=55°,\widehat{F}=63°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{D}+\widehat{E}+\widehat{F}=180°$.

Suy ra $\widehat{D}=180°-\widehat{E}-\widehat{F}$

$\widehat{D}=180°-55°-63°$

$\widehat{D}=62°$

Ta thấy trong tam giác DEF có $\widehat{D}=62°,\widehat{E}=55°,\widehat{F}=63°$ là ba góc nhọn nên tam giác DEF là tam giác nhọn.

Vậy tam giác DEF là tam giác nhọn.

+)

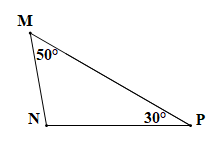
Trên hình vẽ, tam giác MNP có $\widehat{M}=50°,\widehat{P}=30°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{M}+\widehat{N}+\widehat{P}=180°$.

Suy ra $\widehat{N}=180°-\widehat{M}-\widehat{P}$

$\widehat{N}=180°-50°-30°$

$\widehat{N}=100°$

Ta thấy trong tam giác MNP có $\widehat{N}=100°$ là một góc tù nên tam giác MNP là tam giác tù.

Vậy tam giác MNP là tam giác tù.

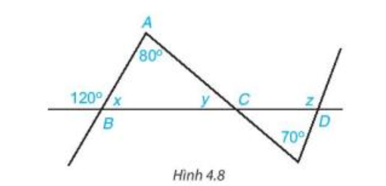
Bài 4.3 trang 62 Toán 7 Tập 1: Tính các số đo x, y, z trong Hình 4.8.

Lời giải:

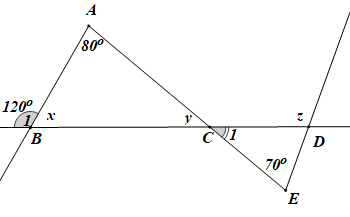
+) Trên hình vẽ ta thấy góc B₁ và góc ABC là hai góc kề bù nên $\widehat{B_1}+\widehat{ABC}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{ABC}=180°-\widehat{B_1}$

Hay $x=\widehat{ABC} =180°–120°=60°.$

+) Xét tam giác ABC có $\widehat{ABC}=60°,\widehat{CAB}=80°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{ABC}+\widehat{BCA}+\widehat{CAB}=180°$

Suy ra $\widehat{BCA}=180°-\widehat{CAB}-\widehat{ABC}$

Hay $y=\widehat{BCA}=180°–80°–60° =40°.$

+) Góc C₁ và góc $\widehat{ACB}$ là hai góc đối đỉnh nên $\widehat{C_1}=\widehat{ACB}=y$ (tính chất hai góc đối đỉnh).

Mà y = 40°.

Do đó $\widehat{C_1}=40°.$

+) Xét tam giác CDE có góc z là góc ngoài của tam giác tại đỉnh D, do đó $z=\widehat{C_1}+\widehat{E}$ (tính chất góc ngoài của một tam giác).

Suy ra z = 40° + 70° = 110°.

Vậy x = 60°, y = 40° và z = 110°.

Lý thuyết Toán 7 Bài 12: Tổng các góc trong một tam giác - Kết nối tri thức

• Tổng ba góc trong một tam giác là tổng số đo ba góc trong tam giác đó.

• Tổng ba góc trong một tam giác bằng 180°.

• Góc ngoài của tam giác là góc kề bù với 1 góc của tam giác.

• Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.

Ví dụ:

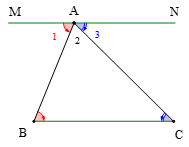
+ Cho tam giác ABC, ta có các góc A₂; góc B; góc C là các góc trong của tam giác.

Qua A kẻ đường thẳng $MN\text{// BC}$. Khi đó ta có:

$\hat{B}=\widehat{A_1}$(hai góc so le trong)

$\hat{C}=\widehat{A_3}$(hai góc so le trong)

Mà $\widehat{A_1}+\widehat{A_2}+\widehat{A_3}=180°$

Nên: $\hat{B}+\widehat{A_2}+\hat{C}=180°$

Do đó tổng ba góc trong tam giác ABC bằng 180°.

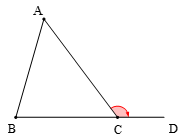
+ Trong hình dưới đây, ta thấy góc ACD kề bù với góc ACB (góc trong tam giác ABC). Do đó góc ACD gọi là góc ngoài của tam giác ABC.

Khi đó ta có: $\widehat{ACD}=\widehat{BAC}+\widehat{ABC}$.

Chú ý:

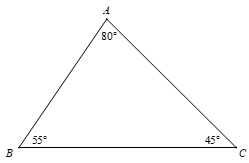
• Tam giác có ba góc đều nhọn được gọi là tam giác nhọn.

Ví dụ: Tam giác ABC có $\hat{A}=80°$; $\hat{B}=55°$; $\hat{C}=45°$. Như vậy các góc A; góc B; góc C đều là góc nhọn. Do đó tam giác ABC gọi là tam giác nhọn.

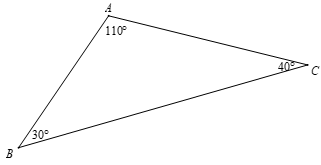
• Tam giác có một góc tù được gọi là tam giác tù.

Ví dụ: Tam giác ABC trong hình dưới đây có $\hat{A}=110°$là góc tù nên tam giác ABC gọi là tam giác tù.

• Tam giác có một góc vuông được gọi là tam giác vuông. Trong tam giác vuông, hai cạnh của góc vuông được gọi là cạnh góc vuông; cạnh còn lại được gọi là cạnh huyền.

• Hai góc có tổng số đo bằng 90° được gọi là hai góc phụ nhau. Trong tam giác vuông hai góc nhọn phụ nhau.

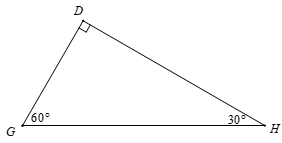
Ví dụ: Tam giác DGH có $\hat{D}=90°$ nên tam giác DGH gọi là tam giác vuông. Cạnh DG và DH gọi là cạnh góc vuông; cạnh GH là cạnh huyền. Góc G và góc H là hai góc phụ nhau.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Luyện tập chung trang 68, trang 69

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Luyện tập chung trang 74

Bài 15: Các trường hợp bằng nhau của tam giác vuông