Toán 7 Bài 9 (Kết nối tri thức): Hai đường thẳng song song và dấu hiệu nhận biết
Với giải bài tập Toán lớp 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 9.
Giải bài tập Toán 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Video giải bài tập Toán 7 Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Mở đầu

Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
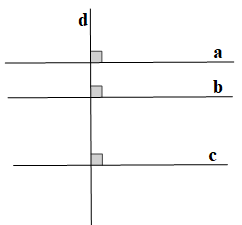
Giả sử các thanh ngang trên mái nhà được mô tả bởi các đường thẳng a, b, c,… như hình vẽ trên.
Vì nên a // b (hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau).
Vì nên a // c (hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau).
Do đó các đường thẳng a, b, c song song với nhau.
Vậy để kiểm tra các thanh ngang trên mái nhà đã song song với nhau chưa, người thợ chỉ cần kiểm tra chúng có cùng vuông góc với một thanh dọc.
1. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
Lời giải:
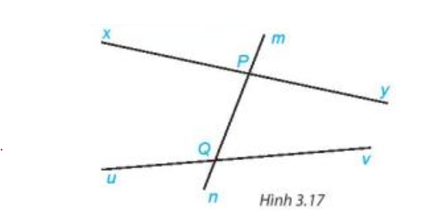
a) Hai cặp góc so le trong trên Hình 3.17 là: góc xPn và mQv; góc yPn và uQm.
b) Bốn cặp góc đồng vị trên Hình 3.17 là: góc xPn và uQn; góc xPm và góc uQm; góc mPy và góc mQv; góc yPn và góc vQn.
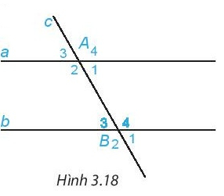
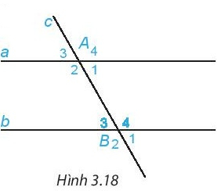
Hãy tính và so sánh hai góc so le trong còn lại A2 và B4.
Lời giải:
+) Trên Hình 3.18 ta có góc A1 và góc A2 là hai góc kề bù nên (tính chất hai góc kề bù).
Suy ra
Mà do đó
+) Góc B3 và góc B4 là hai góc kề bù nên ta có (tính chất hai góc kề bù).
Suy ra
Mà do đó
Vì và nên
Vậy
Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.
Lời giải:
Trên Hình 3.18 ta có hai góc đồng vị là: góc A1 và góc B1.
Góc B1 và góc B3 là hai góc đối đỉnh nên ta có (tính chất hai góc đối đỉnh).
Mà nên
Theo bài ta lại có
Do đó
Vậy hai góc A1 và góc B1 đồng vị với nhau và
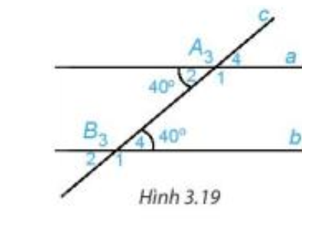
Luyện tập 1 trang 47 Toán 7 Tập 1: Quan sát Hình 3.19
a) Biết Em hãy tính số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính các tổng:
Lời giải:
a) +) Tại đỉnh A:
- Góc A1 kề bù với góc A2 nên ta có (tính chất hai góc kề bù).
Suy ra
Mà , do đó
- Góc A2 và góc A4 là hai góc đối đỉnh nên ta có (tính chất hai góc đối đỉnh).
Mà nên
- Góc A1 và góc A3 là hai góc đối đỉnh nên ta có (tính chất hai góc đối đỉnh).
Mà nên
+) Tại đỉnh B:
- Góc B3 kề bù với góc B4 nên ta có (tính chất hai góc kề bù).
Suy ra
Mà do đó
- Góc B1 và góc B3 là hai góc đối đỉnh nên ta có (tính chất hai góc đối đỉnh).
Mà nên
- Góc B2 và góc B4 là hai góc đối đỉnh nên ta có (tính chất hai góc đối đỉnh).
Mà nên
b) Ta có
2. Dấu hiệu nhận biết hai đường thẳng song song
Luyện tập 2 trang 48 Toán 7 Tập 1:
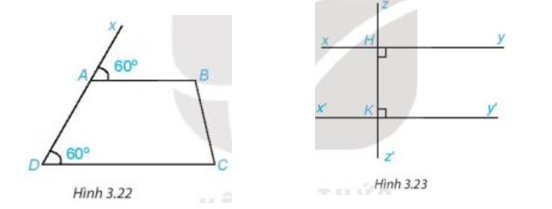
1. Quan sát Hình 3.22 và giải thích vì sao AB // DC.
2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song.
Lời giải:
1.
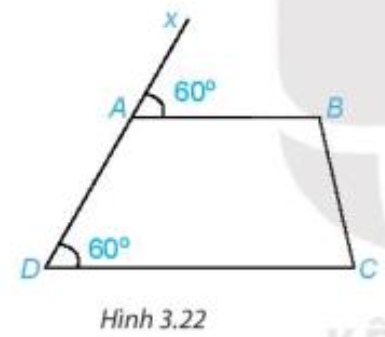
Quan sát Hình 3.22 ta có
Do đó
Mà hai góc này ở vị trí đồng vị.
Suy ra AB // DC (dấu hiệu nhận biết hai đường thẳng song song).
2.
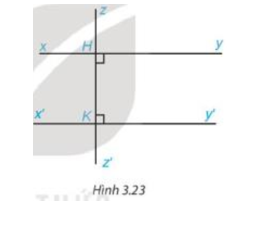
Quan sát Hình 3.23 ta có
Vì và là hai góc kề bù nên ta có (tính chất hai góc kề bù).
Suy ra
Do đó
Mà hai góc này ở vị trí so le trong nên xy // (dấu hiệu nhận biết hai đường thẳng song song).
Tại sao khi vẽ như trên ta lại khẳng định được hai đường thẳng a và b song song với nhau?
Lời giải:
Theo cách vẽ trên thì ta được hình vẽ dưới đây với (góc A1 và góc B1 được vẽ bởi góc nhọn 60o của êke):
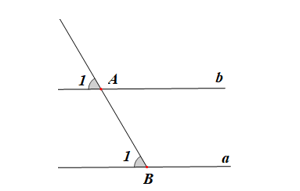
Do đó
Mà hai góc này ở vị trí đồng vị nên a // b (dấu hiệu nhận biết hai dường thẳng song song).
Lời giải:
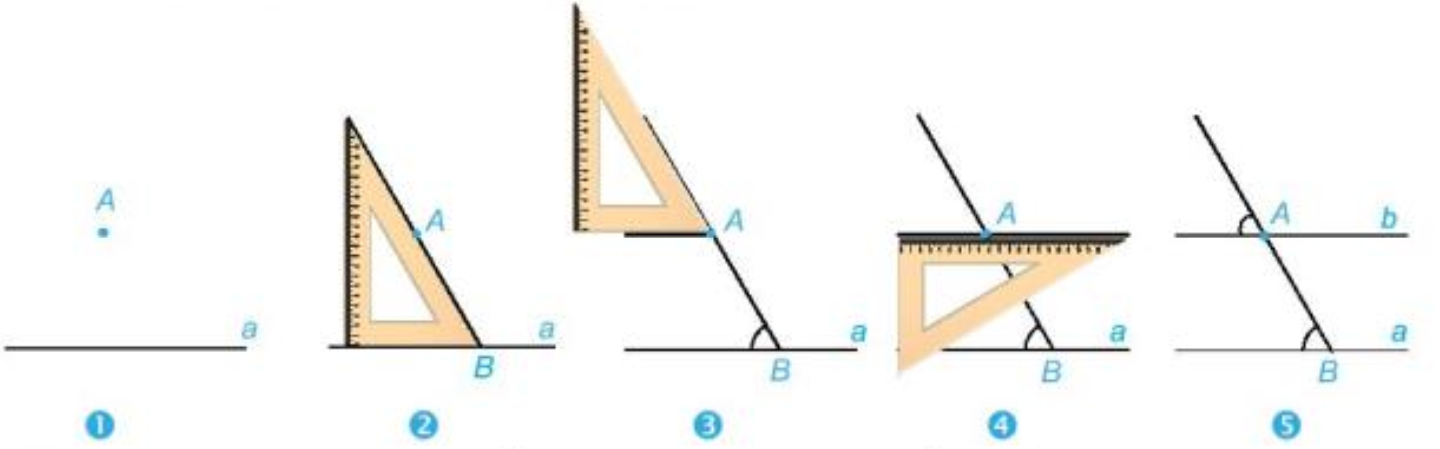
Các bước vẽ đường thẳng b đi qua điểm A và song song với đường thẳng a cho trước được mô tả như hình vẽ dưới đây (sử dụng góc vuông của êke):
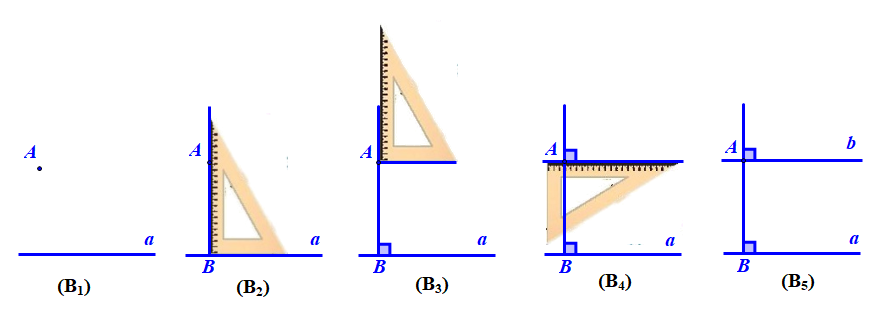
Bài tập
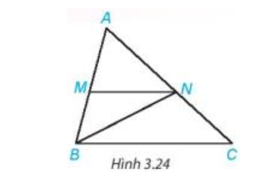
Bài 3.6 trang 49 Toán 7 Tập 1: Quan sát Hình 3.24.
a) Tìm một góc ở vị trí so le trong với góc MNB.
b) Tìm một góc ở vị trí đồng vị với góc ACB.
c) Kể tên một cặp góc trong cùng phía.
d) Biết MN // BC, em hãy kể tên ba cặp góc bằng nhau trong hình vẽ.
Lời giải:
a) Góc ở vị trí so le trong với góc MNB là góc NBC.
b) Góc ở vị trí đồng vị với góc ACB là góc ANM.
c) Một cặp góc trong cùng phía trong hình vẽ là: góc NMB và góc MBC.
d) Ta có MN // BC nên ta có ba cặp góc bằng nhau là:
+) Góc MNB và góc NBC (hai góc ở vị trí so le trong);
+) Góc ACB và góc ANM (hai góc ở vị trí đồng vị);
+) Góc AMN và góc ABC (hai góc ở vị trí đồng vị).
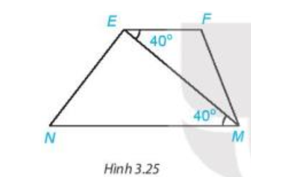
Bài 3.7 trang 49 Toán 7 Tập 1: Quan sát Hình 3.25. Biết Em hãy giải thích tại sao
Lời giải:
Trên Hình 3.25 ta có nên
Mà hai góc này ở vị trí so le trong.
Do đó EF // NM (dấu hiệu nhận biết hai đường thẳng song song).
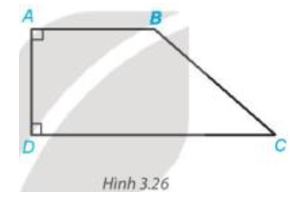
Bài 3.8 trang 49 Toán 7 Tập 1: Quan sát Hình 3.26, giải thích tại sao AB // DC.
Lời giải:
Trên Hình 3.26 ta có AB vuông góc với AD, DC vuông góc với AD
Do đó đường thẳng AB và đường thẳng DC cùng vuông góc với AD nên AB // DC (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau).
Lời giải:
Bước 1: Vẽ đường thẳng d và lấy điểm A không nằm trên đường thẳng d.
Bước 2: Vẽ đường thẳng a đi qua A và vuông góc với đường thẳng d (sử dụng góc vuông của thước êke).
Bước 3: Vẽ đường thẳng d' đi qua A và vuông góc với đường thẳng a (sử dụng góc vuông của thước êke).
Khi đó đường thẳng d' song song với đường thẳng d.
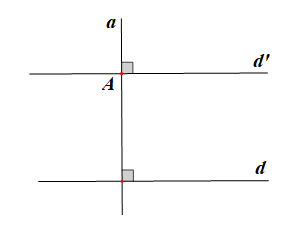
* Giải thích:
Theo hình vẽ trên ta có nên d' // d (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau).
Lời giải:
Bước 1: Lấy hai điểm A và B tuỳ ý.
Bước 2: Vẽ đường thẳng a đi qua A.
Bước 3: Vẽ đường thẳng d đi qua A và vuông góc với đường thẳng a (sử dụng góc vuông của thước êke).
Bước 4: Vẽ đường thẳng b đi qua B và vuông góc với đường thẳng d (sử dụng góc vuông của thước êke).
Khi đó a // b.
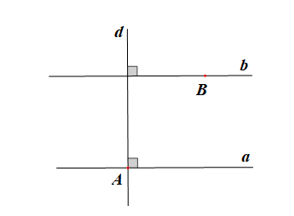
* Giải thích:
Theo hình vẽ trên ta có suy ra a // b (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau).
Bài 3.11 trang 49 Toán 7 Tập 1: Hãy vẽ hai đoạn thẳng AB và MN sao cho AB // MN và AB = MN.
Lời giải:
Bước 1: Vẽ đoạn thẳng AB tuỳ ý.
Bước 2. Vẽ đường thẳng d đi qua A và vuông góc với AB (sử dụng góc vuông của thước êke).
Bước 3: Lấy điểm M trên đường thẳng d.
Bước 4: Vẽ đường thẳng d' đi qua M và vuông góc với đường thẳng d (sử dụng góc vuông của thước êke).
Buớc 5: Trên đường thẳng d' lấy điểm N sao cho MN = AB.
Khi đó AB // MN và AB = MN.
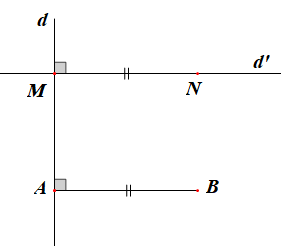
* Giải thích:
Theo hình trên ta có mà điểm M và điểm N nằm trên d' nên
Do nên AB // MN (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau).
Lý thuyết Toán 7 Bài 9. Hai đường thẳng song song và dấu hiệu nhận biết - Kết nối tri thức
1. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
• Cho đường thẳng c cắt hai đường thẳng a và b lần lượt tại A và B tạo thành bốn góc đỉnh A và bốn góc đỉnh B. Khi đó ta có:
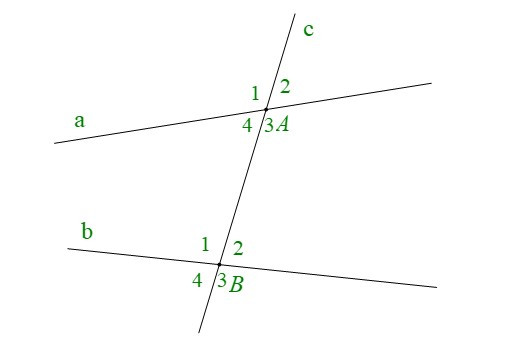
+ Các cặp góc so le trong là: A3 và B1; A4 và B2.
+ Các cặp góc đồng vị là: A1 và B1; A2 và B2; A3 và B3; A4 và B4.
+ Các cặp góc trong cùng phía là: A4 và B1; A3 và B2.
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+ Hai góc so le trong còn lại bằng nhau.
+ Hai góc đồng vị bằng nhau.
Ví dụ:
+ Cho đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại A và B.
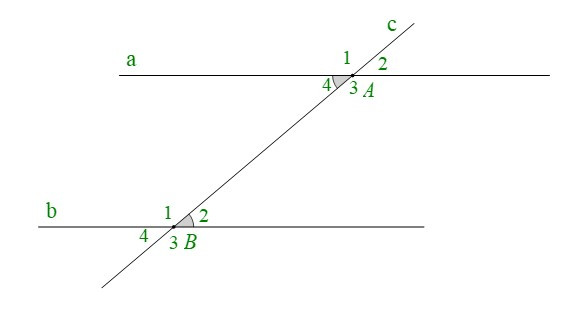
Ta có là cặp góc so le trong
Nếu thì cặp góc so le trong còn lại và các cặp góc đồng vị bằng nhau:
2. Dấu hiệu nhận biết hai đường thẳng song song
• Nếu đường thẳng c cắt hai đường thẳng phân biệt a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau. Kí hiệu là: .
• Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ:
+ Cho hình vẽ:
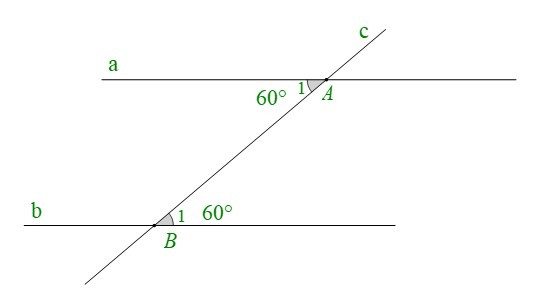
Ta có: . Mà hai góc ở vị trí so le trong.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
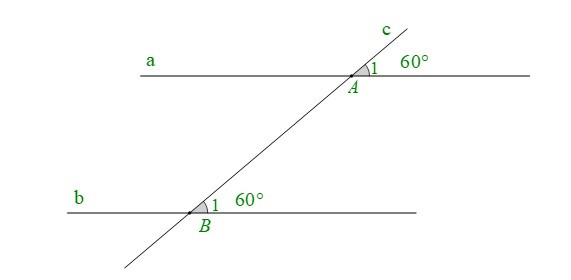
Ta có: . Mà hai góc ở vị trí đồng vị.
Do đó: (dấu hiệu nhận biết hai đường thẳng song song).
+ Cho hình vẽ:
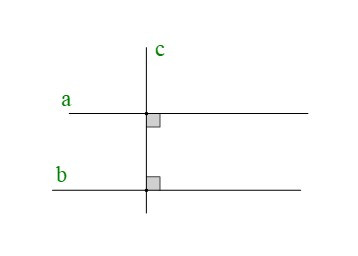
Ta có: và
Do đó: .
Chú ý:
+ Muốn vẽ đường thẳng đi qua một điểm và song song với một đường thẳng cho trước bằng góc 60° của êke ta làm như sau:
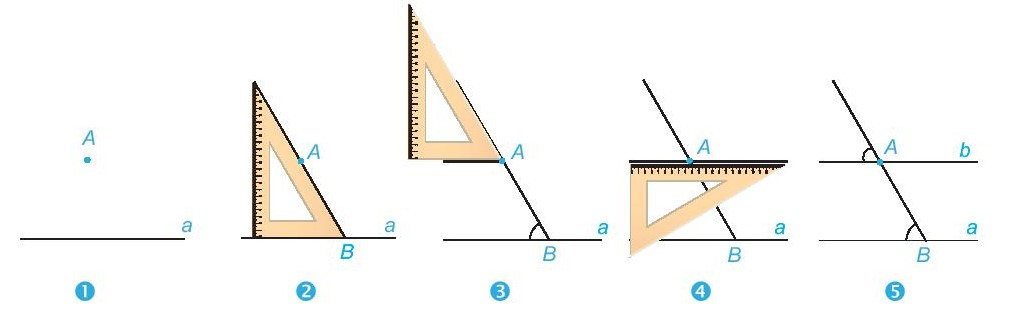
+ Tương tự ta có thể dùng góc vuông hoặc góc 30° của êke (thay cho góc 60°) để vẽ đường thẳng đi qua một điểm và song song với đường thẳng cho trước.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 11: Định lí và chứng minh định lí
Bài tập cuối chương 3 trang 59
Xem thêm tài liệu Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các chương trình khác:
- Giải sgk Lịch sử 7 – Kết nối tri thức
- Lý thuyết Lịch Sử 7 – Kết nối tri thức
- Giải sbt Lịch sử 7 – Kết nối tri thức
- Giải VTH Lịch sử 7 – Kết nối tri thức
- Soạn văn lớp 7 (hay nhất) – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Soạn văn lớp 7 (ngắn nhất) – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Văn mẫu lớp 7 – Kết nối tri thức
- Giải VTH Ngữ văn lớp 7 – Kết nối tri thức
- Giải sgk Địa Lí 7 – Kết nối tri thức
- Lý thuyết Địa Lí 7 – Kết nối tri thức
- Giải sbt Địa lí 7 – Kết nối tri thức
- Giải VTH Địa lí 7 – Kết nối tri thức
- Giải sgk Tiếng Anh 7 Global Success – Kết nối tri thức
- Giải sbt Tiếng Anh 7 Global Success - Kết nối tri thức
- Bài tập Tiếng Anh 7 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 7 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 7 Global success
- Giải sgk Giáo dục công dân 7 – Kết nối tri thức
- Lý thuyết GDCD 7 – Kết nối tri thức
- Giải sbt Giáo dục công dân 7 – Kết nối tri thức
- Giải vth Giáo dục công dân 7 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 7 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Hoạt động trải nghiệm lớp 7 - KNTT
- Giải sgk Hoạt động trải nghiệm 7 - KNTT
- Giải sgk Công nghệ 7 – Kết nối tri thức
- Lý thuyết Công nghệ 7 – Kết nối tri thức
- Giải sbt Công nghệ 7 – Kết nối tri thức
- Giải VTH Công nghệ 7 – KNTT
- Giải sgk Tin học 7 – Kết nối tri thức
- Lý thuyết Tin học 7 – Kết nối tri thức
- Giải sbt Tin học 7 – Kết nối tri thức
- Giải VTH Tin học 7 – Kết nối tri thức
- Giải sgk Giáo dục thể chất 7 – Kết nối tri thức
- Giải sgk Âm nhạc 7 – Kết nối tri thức