Giải Toán 7 Bài 34 (Kết nối tri thức): Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

Giải bài tập Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

A. Các câu hỏi trong bài

Giải Toán 7 trang 72 Tập 2

Mở đầu trang 72 Toán 7 Tập 2:

Hình 9.26 mô phỏng một miếng bìa hình tam giác ABC đặt thăng bằng trên giá nhọn tại điểm G. Điểm đó được xác định như thế nào và có gì đặc biệt?

Lời giải:

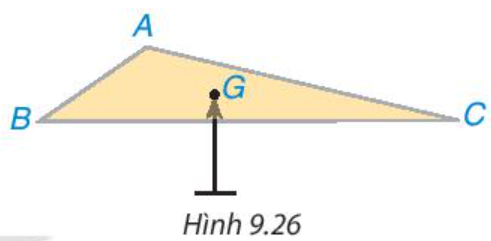
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

G là trọng tâm của tam giác ABC. Trọng tâm là giao điểm của ba đường trung tuyến của tam giác.

Câu hỏi trang 72 Toán 7 Tập 2:

Mỗi tam giác có mấy đường trung tuyến?

Lời giải:

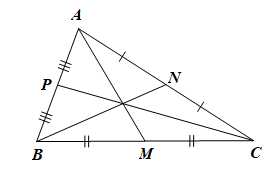
Mỗi tam giác có ba đường trung tuyến xuất phát từ ba đỉnh của tam giác.

HĐ 1 trang 72 Toán 7 Tập 2:

Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi qua đỉnh và trung điểm của cạnh đối diện (tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp (ba đường trung tuyến) có cùng đi qua một điểm không (H.9.28).

Lời giải:

Học sinh thực hiện gấp giấy theo sự hướng dẫn.

Ba nếp gấp (ba đường trung tuyến) cùng đi qua một điểm.

Giải Toán 7 trang 73 Tập 2

HĐ 2 trang 73 Toán 7 Tập 2:

Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A, B, C rồi vẽ tam giác ABC (H.9.29).

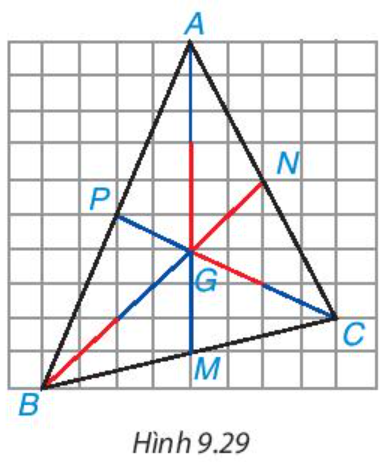
Vẽ hai đường trung tuyến BN, CP, chúng cắt nhau tại G; tia AG cắt BC tại M.

• AM có phải là đường trung tuyến của tam giác ABC không?

• Hãy xác định các tỉ số $\frac{GA}{MA},\frac{GB}{NB},\frac{GC}{PC}.$

Lời giải:

• BM = MC nên M là trung điểm của BC.

AM là đường thẳng nối A và trung điểm M của cạnh BC nên AM là đường trung tuyến của tam giác ABC.

• Ta thấy:

Đoạn MA chia làm 3 phần, GA chiếm 2 phần nên $\frac{GA}{MA}=\frac{2}{3}$;

Đoạn NB chia làm 3 phần, GB chiếm 2 phần nên $\frac{GB}{NB}=\frac{2}{3}$;

Đoạn PC chia làm 3 phần, GC chiếm 2 phần nên $\frac{GC}{PC}=\frac{2}{3}$.

Luyện tập 1 trang 73 Toán 7 Tập 2:

Trong tam giác ABC ở Ví dụ 1, cho trung tuyến BN và GN = 1 cm. Tính GB và NB.

Lời giải:

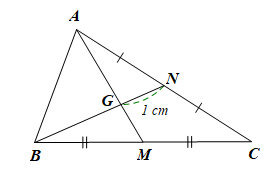
Do G là trọng tâm của tam giác ABC nên $\frac{GB}{NB}=\frac{2}{3}$.

Theo tính chất tỉ lệ thức ta có: $\frac{GB}{NB-GB}=\frac{2}{3-2}$

Suy ra $\frac{GB}{GN}=\frac{2}{1}$ hay GB = 2GN = 2 . 1 = 2 (cm).

Mặt khác $\frac{GB}{NB}=\frac{2}{3}$ nên $\frac{2}{NB}=\frac{2}{3}$. Do đó, NB = 3 (cm).

Vậy GB = 2 cm, NB = 3 cm.

Giải Toán 7 trang 74 Tập 2

Tranh luận trang 74 Toán 7 Tập 2:

Vuông: “Tớ tìm trọng tâm của một tam giác bằng cách lấy giao điểm của hai đường trung tuyến.”.

Tròn: “Tớ còn cách khác nữa cơ.”.

Anh Pi: “Các em có những cách nào?”.

Lời giải:

Các cách để tìm trọng tâm của tam giác:

Cách 1: Lấy giao điểm của hai đường trung tuyến của tam giác.

Ngoài ra ta cũng có thể lấy giao điểm của ba đường trung tuyến của tam giác.

Cách 2. Trên một đường trung tuyến của tam giác, lấy một điểm sao cho khoảng cách từ điểm này đến đỉnh bằng $\frac{2}{3}$ độ dài đường trung tuyến đó.

Vận dụng 1 trang 74 Toán 7 Tập 2:

Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không.

Lời giải:

Học sinh cắt tấm bìa và xác định trọng tâm tam giác theo yêu cầu của đề bài.

Sau khi đặt mảnh bìa lên một giá nhọn tại trọng tâm của tam giác, ta quan sát được mảnh bìa đó thăng bằng trên giá nhọn.

Câu hỏi trang 74 Toán 7 Tập 2:

Mỗi tam giác có mấy đường phân giác?

Lời giải:

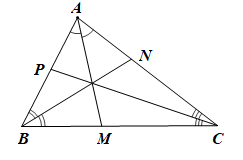
Mỗi tam giác có ba góc nên có ba đường phân giác của tam giác đó.

HĐ 3 trang 74 Toán 7 Tập 2:

Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33).

Lời giải:

Học sinh cắt và gấp theo hướng dẫn.

Sau khi thực hiện cắt và gấp theo hướng dẫn, ta thấy ba nếp gấp đo cùng đi qua một điểm.

Giải Toán 7 trang 75 Tập 2

Luyện tập 2 trang 75 Toán 7 Tập 2:

Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là đường phân giác của góc C không?

Lời giải:

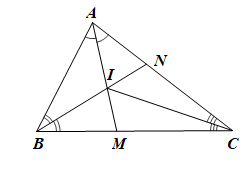
Tam giác ABC có hai đường phân giác AM, BN cắt nhau tại I

Mà ba đường phân giác của tam giác cùng đi qua một điểm

Do đó đường phân giác xuất phát từ đỉnh C của tam giác cũng đi qua điểm I.

Vậy CI là đường phân giác của góc C.

Vận dụng 2 trang 75 Toán 7 Tập 2:

Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

Lời giải:

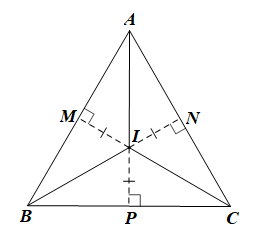
Giả sử $∆$ABC đều có điểm I cách đều ba cạnh của tam giác, tức IM = IN = IP (hình vẽ).

Khi đó điểm I là giao điểm của ba đường phân giác của tam giác ABC.

Do $∆$ABC đều nên $∆$ABC cũng cân tại A.

Theo kết quả Ví dụ 2, trang 75, ta có AI là đường trung tuyến của $∆$ABC.

Chứng minh tương tự, ta cũng có:

• $∆$ABC đều nên $∆$ABC cân tại B, do đó BI là đường trung tuyến của $∆$ABC;

• $∆$ABC đều nên $∆$ABC cân tại C, do đó CI là đường trung tuyến của $∆$ABC.

Suy ra AI, BI, CI là ba đường trung tuyến của $∆$ABC cắt nhau tại điểm I.

Khi đó I là trọng tâm của tam giác ABC.

Vậy trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

B. Bài tập

Giải Toán 7 trang 76 Tập 2

Bài 9.20 trang 76 Toán 7 Tập 2:

Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu “?” để được các đẳng thức:

BG = ? BN, CG = ? CP;

BG = ? GN, CG = ? GP.

Lời giải:

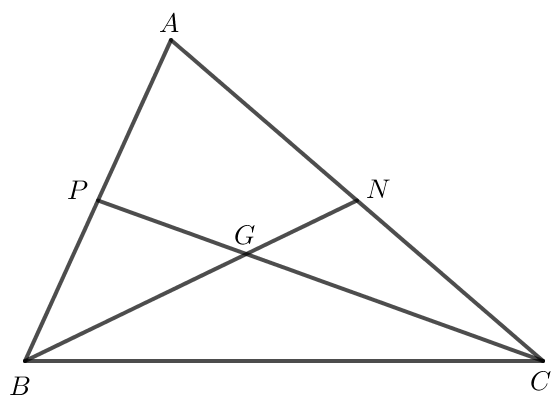
Vì G là trọng tâm của tam giác ABC nên BG = $\frac{2}{3}$BN; CG = $\frac{2}{3}$CP.

Hay $\frac{BG}{BN}=\frac{2}{3}$ và $\frac{CG}{CP}=\frac{2}{3}$

• Từ $\frac{BG}{BN}=\frac{2}{3}$ suy ra $\frac{BG}{BN-BG}=\frac{2}{3-2}$

Do đó $\frac{BG}{GN}=\frac{2}{1}$ hay BG = 2GN.

• Từ $\frac{CG}{CP}=\frac{2}{3}$ suy ra $\frac{CG}{CP-CG}=\frac{2}{3-2}$

Do đó $\frac{CG}{GP}=\frac{2}{1}$ hay CG = 2GP.

Vậy BG = $\frac{2}{3}$BN, CG = $\frac{2}{3}$CP, BG = 2GN, CG = 2GP.

Bài 9.21 trang 76 Toán 7 Tập 2: Chứng minh rằng:

a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.

b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Lời giải:

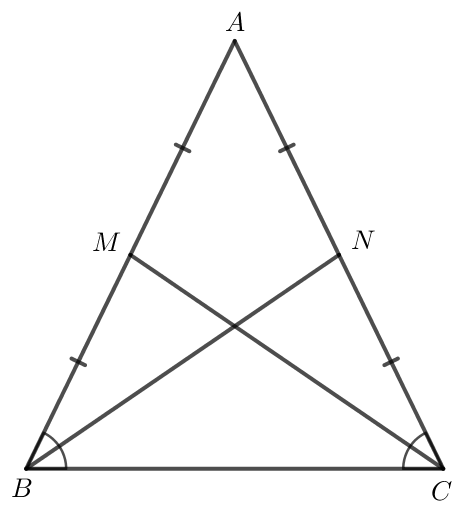
Giả sử $∆$ABC cân tại A có M, N lần lượt là trung điểm của AB và AC.

a) Do $∆$ABC cân tại A nên AB = AC và $\widehat{ABC}=\widehat{ACB}$ (tính chất tam giác cân).

Vì M là trung điểm của AB nên AM = $\frac{1}{2}$AB;

Vì N là trung điểm của AC nên AN = $\frac{1}{2}$AC.

Mà AB = AC nên AM = AN

Xét $∆$ANB và $∆$AMC có:

AM = AN (chứng minh trên).

$\widehat{BAC}$ là góc chung

AB = AC (chứng minh trên).

Suy ra $∆$ANB = $∆$AMC (c.g.c).

Do đó BN = MC (hai cạnh tương ứng).

Vậy trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.

b) Giả sử $∆$ABC có hai trung tuyến CM, BN bằng nhau và cắt nhau tại G.

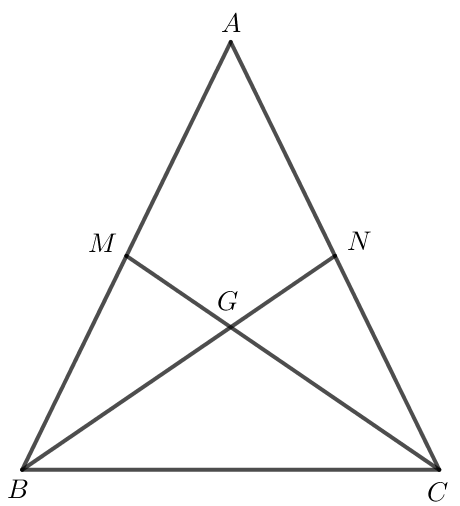
Vì G là giao điểm của hai đường trung tuyến BN và CM của tam giác ABC nên G là trọng tâm tam giác ABC.

Do đó CG = $\frac{2}{3}$CM, BG = $\frac{2}{3}$BN.

Mà CM = BN (giả thiết) nên CG = BG.

$∆$BGC có CG = BG nên $∆$BGC cân tại G.

Suy ra $\widehat{GBC}=\widehat{GCB}$ (tính chất tam giác cân)

Xét $∆$BMC và $∆$CNB có:

MC = NB (theo giả thiết),

$\widehat{MCB}=\widehat{NBC}$ (do $\widehat{GBC}=\widehat{GCB}$),

BC là cạnh chung.

Do đó $∆$BMC = $∆$CNB (c.g.c).

Suy ra $\widehat{MBC}=\widehat{NCB}$ (hai góc tương ứng).

DABC có $\widehat{ABC}=\widehat{ACB}$ nên $∆$ABC cân tại A.

Vậy nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Bài 9.22 trang 76 Toán 7 Tập 2:

Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.

Lời giải:

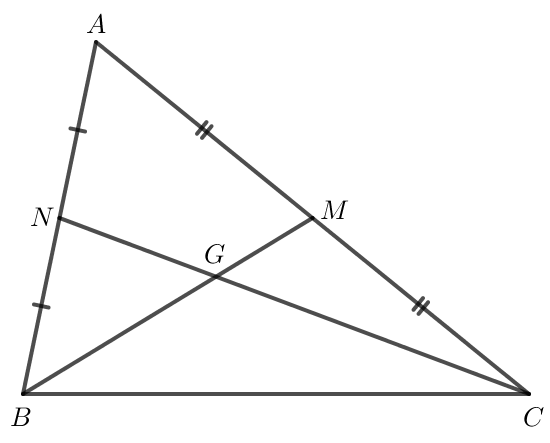
Vì G là trọng tâm của $∆$ABC nên CG = $\frac{2}{3}$CN, BG = $\frac{2}{3}$BM.

Xét $∆$GBC có $\widehat{GBC}>\widehat{GCB}$ nên GC > GB (cạnh đối diện với góc lớn hơn thì lớn hơn).

Khi đó $\frac{2}{3}$CN > $\frac{2}{3}$BM.

Suy ra CN > BM.

Vậy CN > BM.

Bài 9.23 trang 76 Toán 7 Tập 2:

Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC biết góc BAC bằng 120°.

Lời giải:

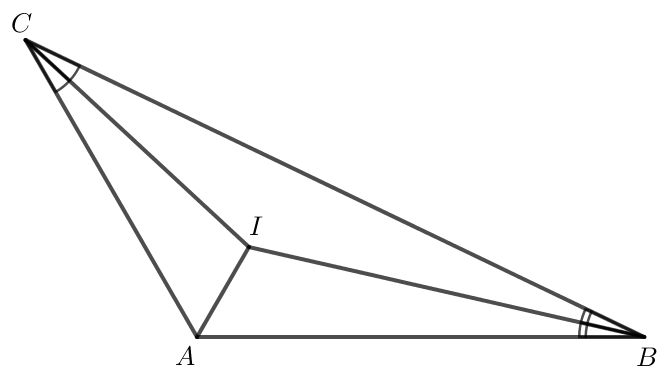
Xét $∆$ABC có $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (tổng ba góc trong một tam giác).

Do đó $\widehat{ABC}+\widehat{ACB}=180°-\widehat{B\text{AC}}$ = 180° - 120° = 60°.

Do BI là tia phân giác của góc ABC nên $\widehat{ABC}=2\widehat{IBC}$.

Do CI là tia phân giác của góc ACB nên $\widehat{ACB}=2\widehat{ICB}$.

Do đó $\widehat{ABC}+\widehat{ACB}=2\left(\widehat{IBC}+\widehat{ICB}\right)$.

Hay 60^o = 2$\left(\widehat{IBC}+\widehat{ICB}\right)$.

Suy ra $\widehat{IBC}+\widehat{ICB}$ = 60° : 2 = 30°.

Xét $∆$IBC có $\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180°$ (tổng ba góc trong một tam giác).

Do đó $\widehat{BIC}=180°-\left(\widehat{IBC}+\widehat{ICB}\right)$ = 180° - 30° = 150°.

Vậy $\widehat{BIC}$ = 150°.

Bài 9.24 trang 76 Toán 7 Tập 2:

Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.

Lời giải:

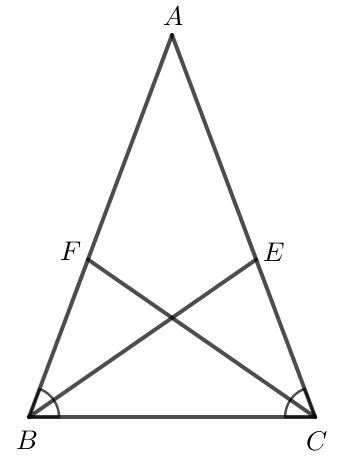
Do BE là tia phân giác của góc ABC nên $\widehat{EBA}=\frac{1}{2}\widehat{ABC}$.

Do CF là tia phân giác của góc ACB nên $\widehat{FCA}=\frac{1}{2}\widehat{ACB}$.

Mà $\widehat{ABC}=\widehat{ACB}$ (do $∆$ABC cân tại A) nên $\widehat{EBA}=\widehat{FCA}$.

Xét $∆$AEB và $∆$AFC có:

$\widehat{EBA}=\widehat{FCA}$ (chứng minh trên),

AB = AC ($∆$ABC cân tại A),

$\widehat{BAC}$ chung

Suy ra $∆$AEB = $∆$AFC (g.c.g)

Do đó CF = BE (hai cạnh tương ứng).

Vậy BE = CF.

Bài 9.25 trang 76 Toán 7 Tập 2:

Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.

a) Hãy giải thích tại sao DP = DR.

b) Hãy giải thích tại sao DP = DQ.

c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A?

Lời giải:

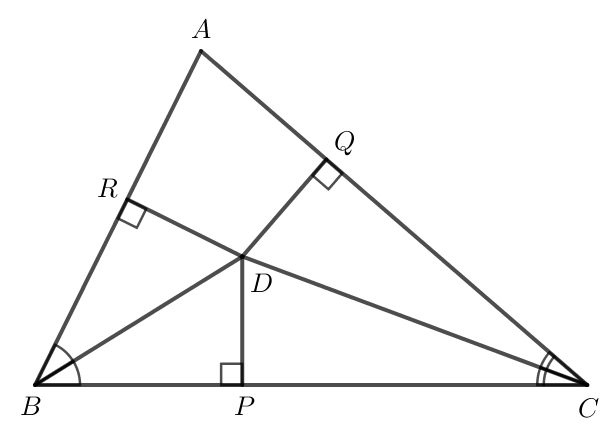
a) Vì D nằm trên tia phân giác BD của góc ABC nên D cách đều hai cạnh BA và BC.

Do đó DR = DP.

b) Vì D nằm trên tia phân giác CD của góc ACB nên D cách đều hai cạnh CB và CA.

Do đó DP = DQ.

c) Từ câu a và b ta có DR = DP và DQ = DP nên DR = DQ.

Ta có D nằm trong góc BAC và D cách đều hai cạnh AB và AC của góc BAC nên D nằm trên tia phân giác của góc BAC.

Vậy D nằm trên tia phân giác của góc BAC.

Lý thuyết Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác - Kết nối tri thức

1. Sự đồng quy của ba đường trung tuyến trong một tam giác

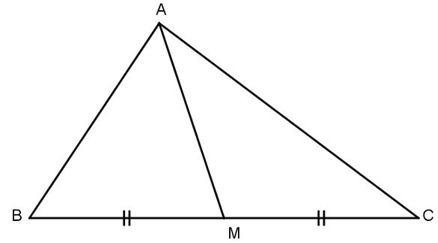
a) Đường trung tuyến của tam giác

Trong hình dưới đây, đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC.

b) Sự đồng quy của ba đường trung tuyến

Định lí 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đó cách mổi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

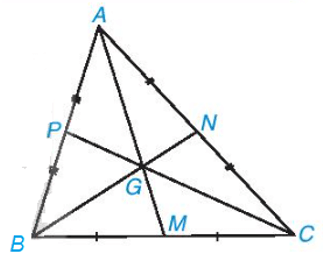
Ví dụ: Trong tam giác ABC có các đường trung tuyến AM, BN, CP đồng quy tại điểm G.

Ta có: $\frac{GA}{MA}=\frac{GB}{NB}=\frac{GC}{PC}=\frac{2}{3}.$

Chú ý: Điểm đồng quy của ba đường trung tuyến gọi là trọng tâm tam giác.

Ví dụ: Tam giác ABC có các đường trung tuyến AM, BN, CP đồng quy tại điểm G.

Khi đó, G được gọi là trọng tâm tam giác ABC.

2. Sự đồng quy của ba đường phân giác trong tam giác

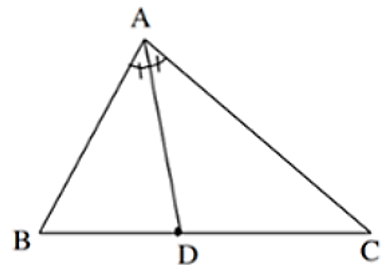
a) Đường phân giác của tam giác

Trong hình dưới đây, cho tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D thì đoạn thẳng AD được gọi là đường phân giác (xuất phát từ đỉnh A) của tam giác ABC.

b) Sự đồng quy của ba đường phân giác

Định lí 2: Ba đường phân giác của một tam giác đồng quy tại một điểm. Điểm này cách đều ba cạnh của tam giác đó.

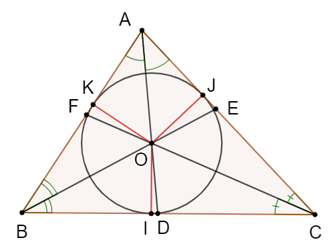
Ví dụ: Trong tam giác ABC có các đường phân giác AD, BE, CF đồng quy tại điểm O.

Ta có: OI = OJ = OK.

Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Luyện tập chung trang 83

Bài tập cuối chương 9

Bài 1: Tập hợp các số hữu tỉ

Bài 2: Cộng, trừ, nhân, chia số hữu tỉ