Toán 7 Bài 15 (Kết nối tri thức): Các trường hợp bằng nhau của tam giác vuông
Với giải bài tập Toán lớp 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 15.
Giải bài tập Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
Video giải bài tập Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
Mở đầu
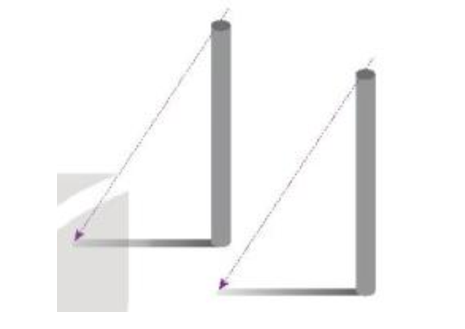
Bạn Vuông: Tớ thấy bóng hai chiếc cột dài bằng nhau, vì sao vậy nhỉ?
Bạn Tròn: Đấy là do hai chiếc cột cao bằng nhau đấy!
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Hình ảnh hai chiếc cột dựng thẳng đứng cao bằng nhau và tia nắng Mặt Trời tạo với hai chiếc cột các góc bằng nhau được mô tả như hình vẽ dưới đây:
|
GT |
ABC vuông tại A, vuông tại A'; AB = A'B', |
|
KL |
AC = A'C'. |
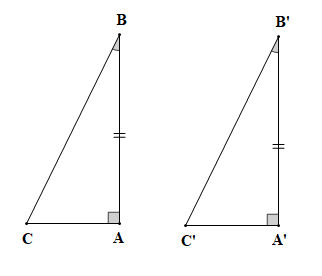
Xét tam giác ABC (vuông tại A) và tam giác A'B'C' (vuông tại A') có:
AB = A'B' (theo giả thiết);
(theo giả thiết).
Vậy (cạnh góc vuông – góc nhọn kề).
Suy ra AC = A'C' (hai góc tương ứng).
Do đó khi tia nắng Mặt Trời tạo với hai chiếc cột bằng nhau các góc bằng nhau thì hai chiếc bóng của hai chiếc cột đó bằng nhau.
Vậy lí do mà bạn Tròn đưa ra là đúng.
1. Ba trường hợp bằng nhau của tam giác vuông
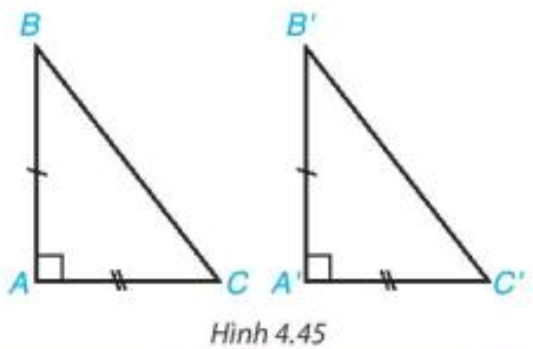
AB = A'B', AC = A'C' (H.4.45).
Lời giải:
|
GT |
ABC vuông tại A, vuông tại A'; AB = A'B', AC = A'C'. |
|
KL |
(c.g.c). |
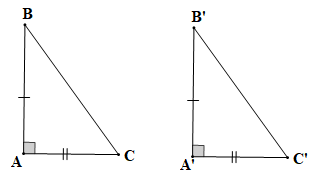
Tam giác ABC vuông tại A (theo giả thiết) nên
Tam giác A'B'C' vuông tại A' (theo giả thiết) nên
Do đó
Xét tam giác ABC và tam giác A'B'C' có:
AB = A'B' (theo giả thiết);
(chứng minh trên);
AC = A'C' (theo giả thiết).
Vậy (c.g.c).
Lời giải:
|
GT |
ABC vuông tại A, vuông tại A'; AB = A'B', |
|
KL |
(g.c.g). |
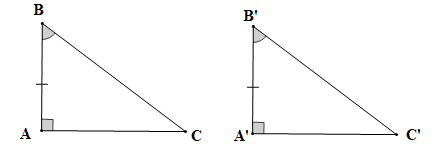
Tam giác ABC vuông tại A (theo giả thiết) nên
Tam giác A'B'C' vuông tại A' (theo giả thiết) nên
Do đó
Xét tam giác ABC và tam giác A'B'C' có:
(chứng minh trên);
AB = A'B' (theo giả thiết);
(theo giả thiết).
Vậy (g.c.g).
Luyện tập 1 trang 76 Toán 7 Tập 1: Quay trở lại tình huống mở đầu, ta thấy mỗi chiếc cột với bóng của nó tạo thành hai cạnh góc vuông của một tam giác vuông. Hai tam giác vuông này có hai cặp cạnh tương ứng bằng nhau và hai góc ở đỉnh chiếc cột của hai tam giác này cũng bằng nhau. Vậy lí do mà bạn Tròn đưa ra có đúng không?
Lời giải:
Hình ảnh hai chiếc cột dựng thẳng đứng cao bằng nhau và tia nắng Mặt Trời tạo với hai chiếc cột các góc bằng nhau được mô tả như hình vẽ dưới đây:
|
GT |
ABC vuông tại A, vuông tại A'; AB = A'B', |
|
KL |
AC = A'C' . |
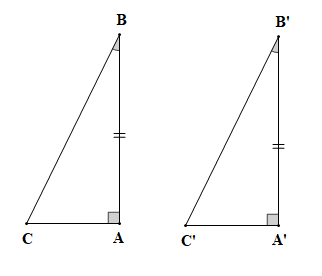
Xét tam giác ABC (vuông tại A) và tam giác A'B'C' (vuông tại A') có:
AB = A'B' (theo giả thiết);
(theo giả thiết).
Vậy (cạnh góc vuông – góc nhọn kề).
Suy ra AC = A'C' (hai góc tương ứng).
Do đó khi tia nắng Mặt Trời tạo với hai chiếc cột bằng nhau các góc bằng nhau thì hai chiếc bóng của hai chiếc cột đó bằng nhau.
Vậy lí do mà bạn Tròn đưa ra là đúng.
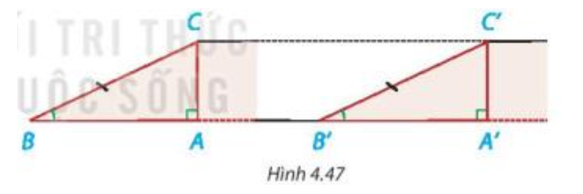
b) So sánh độ cao của hai con dốc.
Lời giải:
Hình ảnh hai con dốc trong đề bài được mô tả bởi hình vẽ dưới đây:
|
GT |
ABC vuông tại A, vuông tại A'; BC = B'C', |
|
KL |
AC = A'C'. |
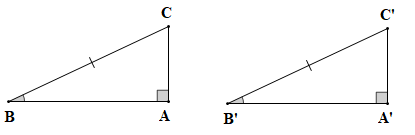
+) Tam giác ABC vuông tại A nên hai góc nhọn của tam giác phụ nhau.
Do đó Suy ra
Tam giác A'B'C' vuông tại A' nên hai góc nhọn của tam giác phụ nhau.
Do đó Suy ra
Mà (theo giả thiết).
Do đó .
Suy ra
Xét tam giác ABC và tam giác A'B'C' có:
(theo giả thiết);
BC = B'C' (theo giả thiết);
(chứng minh trên).
Vậy (g.c.g).
b) Từ (chứng minh câu a) suy ra AC = A'C' (hai cạnh tương ứng).
Vậy độ cao của hai con dốc đó bằng nhau.
Lời giải:
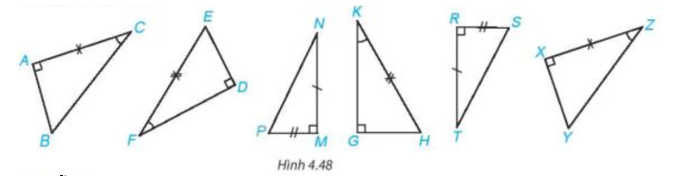
+) Xét tam giác ABC (vuông tại A) và tam giác XYZ (vuông tại X) có:
AC = XZ (theo giả thiết);
(theo giả thiết).
Vậy (cạnh góc vuông – góc nhọn kề).
+) Xét tam giác DEF (vuông tại D) và tam giác GHK (vuông tại G) có:
EF = HK (theo giả thiết);
(theo giả thiết).
Vậy (cạnh huyền – góc nhọn).
+) Xét tam giác MNP (vuông tại M) và tam giác RTS (vuông tại R) có:
MN = RT (theo giả thiết);
MP = RS (theo giả thiết).
Vậy (hai cạnh góc vuông).
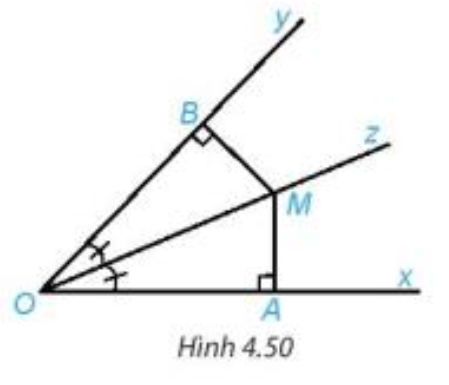
Lời giải:
|
GT |
Tia Oz là tia phân giác của góc xOy; , tại A, tại B. |
|
KL |
MA = MB. |
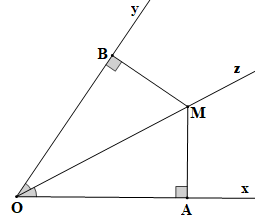
Tia Oz là tia phân giác của góc xOy nên (tính chất tia phân giác của một góc).
Hay .
Vì tại A nên tại B nên .
Do đó tam giác OAM vuông tại A và tam giác OBM vuông tại B.
Xét tam giác OAM (vuông tại A) và tam giác OBM (vuông tại B) có:
OM là cạnh chung;
(chứng minh trên).
Vậy (cạnh huyền – góc nhọn).
Suy ra MA = MB (hai cạnh tương ứng).
2. Trường hợp bằng nhau đặc biệt của tam giác vuông
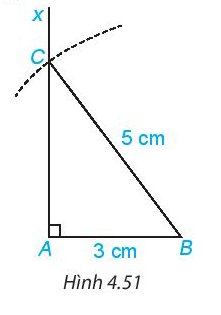
HĐ 4 trang 78 Toán 7 Tập 1: Vẽ tam giác vuông ABC có AB = 3 cm, BC = 5 cm theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm.
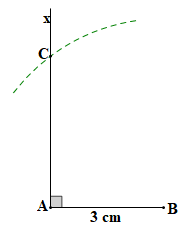
- Vẽ tia Ax vuông góc với AB và cung tròn tâm B bán kính 5 cm như Hình 4.51.
Cung tròn cắt tia Ax tại điểm C.
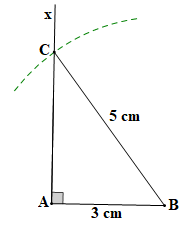
- Vẽ đoạn thẳng BC ta được tam giác ABC.
Lời giải:
Bước 1. Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm ta được hình vẽ dưới đây:
![]()
Bước 2. Vẽ tia Ax vuông góc với AB và cung tròn tâm B bán kính 5 cm, cung tròn cắt tia Ax tại điểm C như hình dưới đây
Bước 3. Vẽ đoạn thẳng BC ta được tam giác ABC như hình vẽ sau:
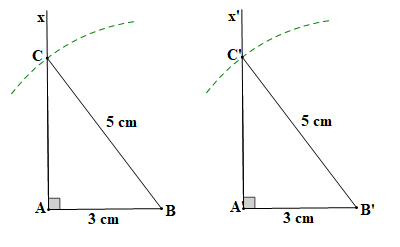
HĐ 5 trang 77 Toán 7 Tập 1: Tương tự, vẽ thêm tam giác A'B'C' có A'B' = 3 cm, B'C' = 5 cm.
a) Dùng thước thẳng có vạch chia hoặc compa kiểm tra xem AC có bằng A'C' không.
b) Hai tam giác ABC và A'B'C' có bằng nhau không?
Lời giải:
Thực hiện tương tự như Hoạt động 4, ta vẽ được tam giác A'B'C' thỏa mãn yêu cầu.
Ta có hình vẽ:
a) Dùng thước thẳng có vạch chia để đo độ dài hai đoạn thẳng AC và A'C' ta được:
AC = 4 cm, A'C' = 4 cm.
Do đó AC = A'C'.
b) Hai tam giác ABC (vuông tại A) và A'B'C' (vuông tại A') có:
AB = A'B' (= 3 cm); AC = A'C' (= 4 cm).
Vậy (hai cạnh góc vuông).
Câu hỏi trang 78 Toán 7 Tập 1:
Hãy chỉ ra các cặp tam giác vuông bằng nhau dưới đây.
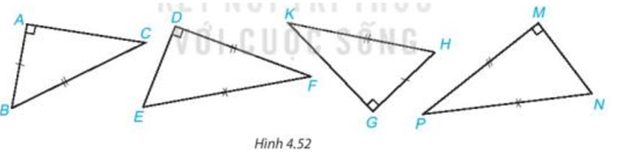
Lời giải:
+)
Xét tam giác ABC (vuông tại A) và tam giác GHK (vuông tại G) có:
AB = GH, BC = HK.
Vậy (cạnh huyền – cạnh góc vuông).
+)
Xét tam giác DEF (vuông tại D) và tam giác MNP (vuông tại M) có:
DF = MP, EF = NP.
Vậy (cạnh huyền – cạnh góc vuông).
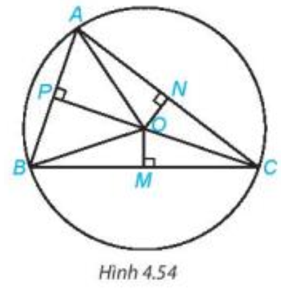
Lời giải:
Ba điểm A, B, C nằm trên đường tròn tâm O nên ta có OA = OB = OC.
+)
Xét tam giác OAP (vuông tại P) và tam giác OBP (vuông tại P) có:
OA = OB (chứng minh trên);
OP là cạnh chung.
Vậy (cạnh huyền – cạnh góc vuông).
+) .
Xét tam giác OBM (vuông tại M) và tam giác OCM (vuông tại M) có:
OB = OC (chứng minh trên);
OM là cạnh chung.
Vậy (cạnh huyền – cạnh góc vuông).
+) .
Xét tam giác OAN (vuông tại N) và tam giác OCN (vuông tại N) có:
OA = OC (chứng minh trên);
ON là cạnh chung.
Vậy (cạnh huyền – cạnh góc vuông).
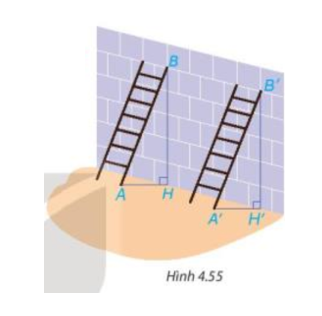
Lời giải:
Hai chiếc thang dài như nhau dựa vào bức tường với cùng độ cao được mô tả dưới hình vẽ sau:
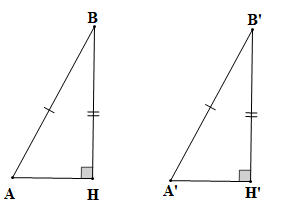
|
GT |
, ; , ; AB = A'B', BH = B'H'. |
|
KL |
. |
Xét tam giác ABH (vuông tại H) và tam giác B'A'H' (vuông tại H') có:
AB = A'B' (theo giả thiết);
BH = B'H' (theo giả thiết).
Vậy (cạnh huyền – cạnh góc vuông).
Suy ra (hai góc tương ứng).
Vậy .
Bài tập
Bài 4.20 trang 79 Toán 7 Tập 1:
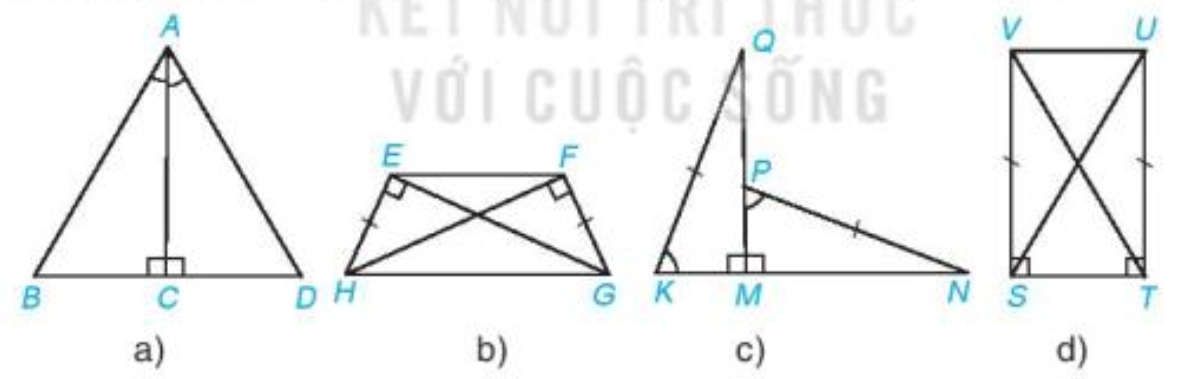
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
Lời giải:
a)
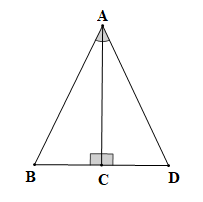
Xét tam giác ABC (vuông tại C) và tam giác ADC (vuông tại C) có:
AC là cạnh chung, (theo giả thiết).
Vậy (cạnh góc vuông – góc nhọn kề).
b)
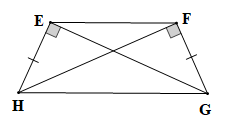
Xét tam giác EGH (vuông tại E) và tam giác FHG (vuông tại F) có:
EH = FG (theo giả thiết), GH là cạnh chung.
Vậy (cạnh huyền – cạnh góc vuông).
c)
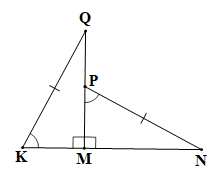
Xét tam giác MNP(vuông tại M) và tam giác MQK (vuông tại M) có:
NP = QK (theo giả thiết), (theo giả thiết).
Vậy (cạnh huyền – góc nhọn).
d)
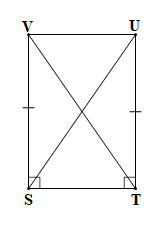
Xét tam giác SVT (vuông tại S) và tam giác TUS (vuông tại T) có:
SV = TU (theo giả thiết); ST là cạnh chung.
Vậy (hai cạnh góc vuông).
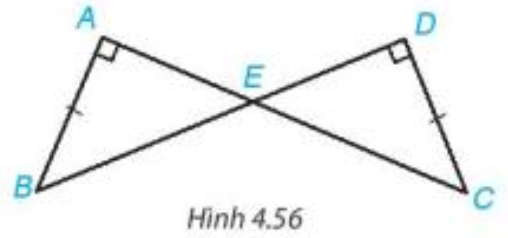
Bài 4.21 trang 79 Toán 7 Tập 1: Cho Hình 4.56, biết AB = CD, Chứng minh rằng
Lời giải:
|
GT |
AB = CD, |
|
KL |
|
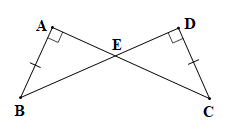
Chứng minh (hình vẽ trên):
Theo giả thiết ta có tam giác ABE vuông tại A và tam giác DCE vuông tại D.
Tam giác ABE vuông tại A nên hai góc nhọn của tam giác phụ nhau.
Tức là suy ra
Tam giác DCE vuông tại D nên hai góc nhọn của tam giác phụ nhau.
Tức là suy ra .
Mà (hai góc đối đỉnh).
Do đó hay .
Xét tam giác ABE (vuông tại A) và tam giác DCE (vuông tại D) có:
AB = DC (theo giả thiết);
(chứng minh trên).
Vậy (cạnh góc vuông – góc nhọn kề).
Bài 4.22 trang 79 Toán 7 Tập 1: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Lời giải:
|
GT |
ABCD là hình chữ nhật; M là trung điểm BC. |
|
KL |
. |
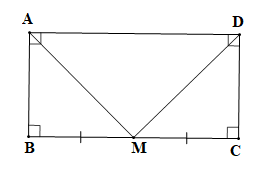
Chứng minh (hình vẽ trên):
ABCD là hình chữ nhật (theo giả thiết) nên và AB = CD.
Do đó tam giác ABM vuông tại B và tam giác DCM vuông tại C.
M là trung điểm cạnh BC nên MB = MC (định nghĩa trung điểm của đoạn thẳng).
Xét tam giác ABM (vuông tại B) và tam giác DCM (vuông tại C) có:
AB = DC (chứng minh trên);
MB = MC (chứng minh trên).
Vậy (hai cạnh góc vuông).
Lý thuyết Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông - Kết nối tri thức
1. Ba trường hợp bằng nhau của tam giác vuông
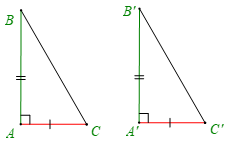
• Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
AB = A'B'; AC = A'C'. Khi đó = (hai cạnh góc vuông).
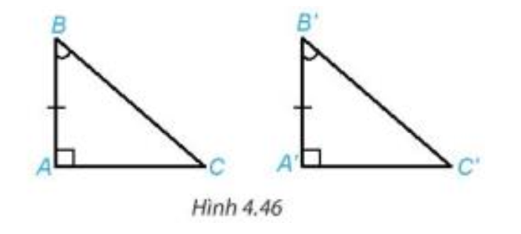
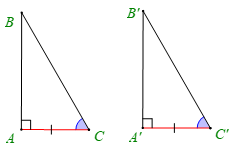
• Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
AC = A'C'; . Khi đó = (cạnh góc vuông – góc nhọn kề).
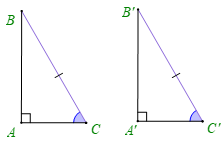
• Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại <A'có:
BC = B'C'; . Khi đó = (cạnh huyền – góc nhọn).
2. Trường hợp bằng nhau đặc biệt của tam giác vuông
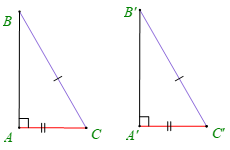
• Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
BC = B'C'; AC = A'C'. Khi đó = <(cạnh huyền – cạnh góc vuông).
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Luyện tập chung trang 85, trang 86
Bài tập cuối chương 4 trang 87
Xem thêm các chương trình khác:
- Giải sgk Lịch sử 7 – Kết nối tri thức
- Lý thuyết Lịch Sử 7 – Kết nối tri thức
- Giải sbt Lịch sử 7 – Kết nối tri thức
- Giải VTH Lịch sử 7 – Kết nối tri thức
- Soạn văn lớp 7 (hay nhất) – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Soạn văn lớp 7 (ngắn nhất) – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Văn mẫu lớp 7 – Kết nối tri thức
- Giải VTH Ngữ văn lớp 7 – Kết nối tri thức
- Giải sgk Địa Lí 7 – Kết nối tri thức
- Lý thuyết Địa Lí 7 – Kết nối tri thức
- Giải sbt Địa lí 7 – Kết nối tri thức
- Giải VTH Địa lí 7 – Kết nối tri thức
- Giải sgk Tiếng Anh 7 Global Success – Kết nối tri thức
- Giải sbt Tiếng Anh 7 Global Success - Kết nối tri thức
- Bài tập Tiếng Anh 7 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 7 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 7 Global success
- Giải sgk Giáo dục công dân 7 – Kết nối tri thức
- Lý thuyết GDCD 7 – Kết nối tri thức
- Giải sbt Giáo dục công dân 7 – Kết nối tri thức
- Giải vth Giáo dục công dân 7 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 7 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Hoạt động trải nghiệm lớp 7 - KNTT
- Giải sgk Hoạt động trải nghiệm 7 - KNTT
- Giải sgk Công nghệ 7 – Kết nối tri thức
- Lý thuyết Công nghệ 7 – Kết nối tri thức
- Giải sbt Công nghệ 7 – Kết nối tri thức
- Giải VTH Công nghệ 7 – KNTT
- Giải sgk Tin học 7 – Kết nối tri thức
- Lý thuyết Tin học 7 – Kết nối tri thức
- Giải sbt Tin học 7 – Kết nối tri thức
- Giải VTH Tin học 7 – Kết nối tri thức
- Giải sgk Giáo dục thể chất 7 – Kết nối tri thức
- Giải sgk Âm nhạc 7 – Kết nối tri thức