Giải Toán 7 Bài 33 (Kết nối tri thức): Quan hệ giữa ba cạnh của một tam giác

Giải bài tập Toán 7 Bài 33: Quan hệ giữa ba cạnh của một tam giác

A. Các câu hỏi trong bài

Giải Toán 7 trang 66 Tập 2

Mở đầu trang 66 Toán 7 Tập 2:

Một trạm biến áp và một khu dân cư ở hai bên bờ sông (H.9.14). Trên bờ sông phía khu dân cư, hãy tìm một địa điểm C để dựng một cột điện kéo điện từ cột điện A của trạm biến áp đến cột điện B của khu dân cư sao cho tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất.

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

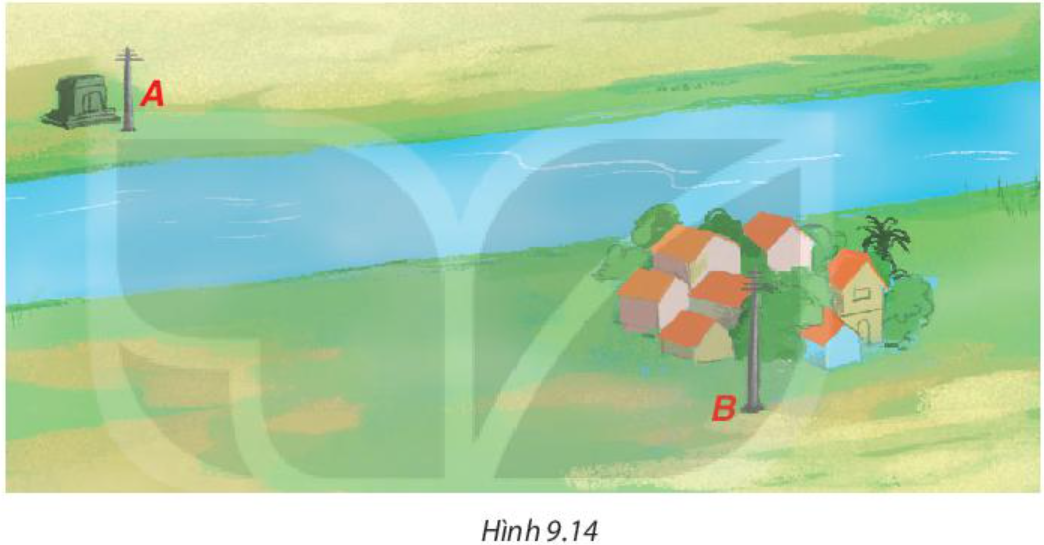
Độ dài dây dẫn điện cần sử dụng để kéo điện từ cột điện A đến cột điện B thông qua cột điện C là AC + CB.

Ta xét các trường hợp:

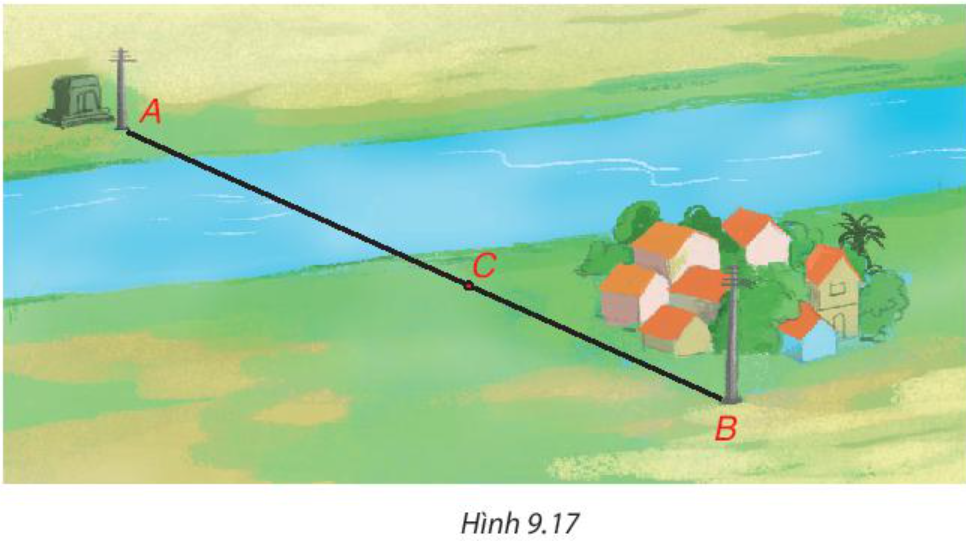
• C thuộc đoạn thẳng AB hay C nằm giữa A và B thì AC + CB = AB.

• C thuộc đường thẳng AB nhưng không thuộc đoạn thẳng AB thì AC + CB > AB.

• C không thuộc đường thẳng AB thì ta có $∆$ABC

Theo bất đẳng thức tam giác, ta có AC + BC > AB.

Khi đó với C bất kì thì AC + CB ≥ AB.

Do đó AC + CB nhỏ nhất khi AC + CB = AB.

Mà AC + CB = AB khi C nằm giữa A và B.

Vậy C nằm giữa A và B thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất.

HĐ 1 trang 66 Toán 7 Tập 2:

Cho hai bộ ba thanh tre nhỏ có độ dài như sau:

Bộ thứ nhất: 10 cm, 20 cm, 25 cm;

Bộ thứ hai: 5 cm, 15 cm, 25 cm.

Em hãy ghép và cho biết bộ nào ghép được thành một tam giác.

Lời giải:

Sau khi thực hành ghép ba thanh tre, kết quả thu được bộ thứ nhất ghép được thành tam giác, bộ thứ hai không ghép được thành tam giác.

HĐ 2 trang 66 Toán 7 Tập 2:

Với bộ ba thanh tre ghép lại được thành một tam giác trong HĐ1, em hãy so sánh độ dài của thanh bất kì với tổng độ dài của hai thanh còn lại.

Lời giải:

Ta có 20 cm + 25 cm = 45 cm > 10 cm;

10 cm + 20 cm = 30 cm > 25 cm;

10 cm + 25 cm = 35 cm > 20 cm.

Vậy độ dài của thanh bất kì luôn nhỏ hơn tổng độ dài của hai thanh còn lại.

Giải Toán 7 trang 67 Tập 2

Tranh luận trang 67 Toán 7 Tập 2:

Vuông: “Ba đoạn thẳng có độ dài 1 cm, 2 cm, 4 cm ghép được thành một tam giác vì

2 < 4 + 1”.

Tròn: “Vuông sai rồi”.

Ý kiến của em thì sao?

Lời giải:

Bạn Tròn nói đúng vì trong một tam giác, độ dài một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại. Tức là bất kì cạnh nào cũng vậy.

Ở đây ta thấy, 1 + 2 = 3 < 4 nên có một cạnh không thỏa mãn một bất đẳng thức tam giác.

Do đó, ba đoạn thẳng đã cho không tạo thành tam giác.

Giải Toán 7 trang 68 Tập 2

Luyện tập trang 68 Toán 7 Tập 2:

Hỏi ba độ dài nào sau đây không thể là độ dài ba cạnh của một tam giác? Vì sao? Hãy vẽ tam giác nhận ba độ dài còn lại làm độ dài ba cạnh.

a) 5 cm, 4 cm, 6 cm.

b) 3 cm, 6 cm, 10 cm.

Lời giải:

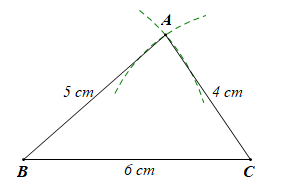
a) Ta có 6 < 5 + 4, ba độ dài 5 cm, 4 cm, 6 cm thỏa mãn điều kiện độ dài lớn nhất nhỏ hơn tổng hai độ dài còn lại nên đây có thể là độ dài ba cạnh của một tam giác.

Dùng thước và compa ta vẽ được hình như sau:

b) Ta có 3 + 6 < 10, ba độ dài 3 cm, 6 cm, 10 cm không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.

Vận dụng trang 68 Toán 7 Tập 2:

Trở lại tình huống mở đầu, em hãy giải thích vì sao nếu dựng cột điện ở vị trí C trên đoạn thẳng AB thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất (H.9.17).

Lời giải:

Độ dài dây dẫn điện cần sử dụng để kéo điện từ cột điện A đến cột điện B thông qua cột điện C là AC + CB.

Ta xét các trường hợp:

• C thuộc đoạn thẳng AB hay C nằm giữa A và B thì AC + CB = AB.

• C thuộc đường thẳng AB nhưng không thuộc đoạn thẳng AB thì AC + CB > AB.

• C không thuộc đường thẳng AB thì ta có $∆$ABC

Theo bất đẳng thức tam giác, ta có AC + BC > AB.

Khi đó với C bất kì thì AC + CB ≥ AB.

Do đó AC + CB nhỏ nhất khi AC + CB = AB.

Mà AC + CB = AB khi C nằm giữa A và B.

Vậy C nằm giữa A và B thì tổng độ dài dây dẫn điện cần sử dụng là ngắn nhất.

B. Bài tập

Giải Toán 7 trang 69 Tập 2

Bài 9.10 trang 69 Toán 7 Tập 2:

Cho các bộ ba đoạn thẳng có độ dài như sau:

a) 2 cm, 3 cm, 5 cm;

b) 3 cm, 4 cm, 6 cm;

c) 2 cm, 4 cm, 5 cm.

Lời giải:

a) Nhận thấy 2 + 3 = 5, bộ ba đoạn thẳng có độ dài 2 cm, 3 cm, 5 cm không thỏa mãn một bất đẳng thức tam giác nên không là độ dài ba cạnh của một tam giác.

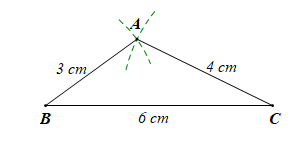
b) Ta có 6 < 3 + 4, bộ ba đoạn thẳng có độ dài 3 cm, 4 cm, 6 cm thỏa mãn độ dài lớn nhất nhỏ hơn tổng hai độ dài còn lại nên có thể là độ dài ba cạnh của một tam giác.

Sử dụng thước thẳng và compa, ta có hình như sau:

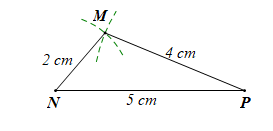
c) Ta có 5 < 2 + 4, bộ ba đoạn thẳng có độ dài 2 cm, 4 cm, 5 cm thỏa mãn độ dài lớn nhất nhỏ hơn tổng hai độ dài còn lại nên có thể là độ dài ba cạnh của một tam giác.

Sử dụng thước thẳng và compa, ta có hình như sau:

Bài 9.11 trang 69 Toán 7 Tập 2:

a) Cho tam giác ABC có AB = 1 cm và BC = 7 cm. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên (cm).

b) Cho tam giác ABC có AB = 2 cm, BC = 6 cm và BC là cạnh lớn nhất. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên (cm).

Lời giải:

a) Áp dụng bất đẳng thức tam giác vào tam giác ABC ta có:

BC - AB < CA < BC + AB

Do đó 7 – 1 < CA < 7 + 1

Hay 6 < CA < 8.

Mà độ dài CA là một số nguyên nên CA = 7 cm.

b) Áp dụng bất đẳng thức tam giác vào tam giác ABC ta có:

BC - AB < CA < BC + AB

Do đó 6 – 2 < CA < 6 + 2

Hay 4 < CA < 8.

Do BC là cạnh lớn nhất trong tam giác nên CA ≤ BC.

Do đó 4 < CA ≤ 6.

Mà độ dài cạnh CA là một số nguyên nên CA = 5 cm hoặc CA = 6 cm.

Bài 9.12 trang 69 Toán 7 Tập 2:

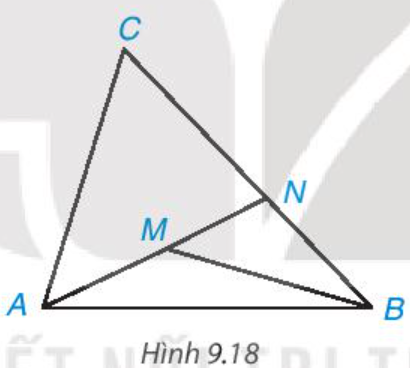
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.18).

a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB.

b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB.

c) Chứng minh MA + MB < CA + CB.

Lời giải:

a) Áp dụng bất đẳng thức tam giác vào $∆$MNB có:

MB < MN + NB (độ dài một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại)

Cộng cả hai vế với MA ta được:

MA + MB < MA + MN + NB.

MA + MB < (MA + MN) + NB

Hay MA + MB < NA + NB.

b) Áp dụng bất đẳng thức tam giác vào $∆$ANC có:

NA < CA + CN (độ dài một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại)

Cộng cả hai vế với NB ta được:

NA + NB < CA + CN + NB.

NA + NB < CA + (CN + NB)

Hay NA + NB < CA + CB.

c) Do MA + MB < NA + NB và NA + NB < CA + CB

Nên MA + MB < NA + NB < CA + CB.

Do đó MA + MB < CA + CB.

Bài 9.13 trang 69 Toán 7 Tập 2:

Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.

Lời giải:

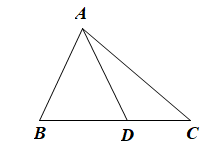
Trong tam giác ABD, theo bất đẳng thức tam giác ta có:

AD < AB + BD (1)

Trong tam giác ACD, theo bất đẳng thức tam giác ta có:

AD < AC + CD (2)

Từ (1) và (2) ta có:

AD + AD < AB + BD + AC + CD

Do đó 2AD < AB + AC + (BD + CD)

Hay 2AD < AB + AC + BC

Suy ra AD < $\frac{1}{2}$(AB + AC + BC).

Mà chu vi tam giác ABC là AB + AC + BC.

Nên AD nhỏ hơn nửa chu vi tam giác ABC.

Vậy AD nhỏ hơn nửa chu vi tam giác ABC.

Lý thuyết Toán 7 Bài 33: Quan hệ giữa ba cạnh của một tam giác - Kết nối tri thức

1. Bất đẳng thức tam giác

Định lí: Trong một tam giác, độ dài của một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại.

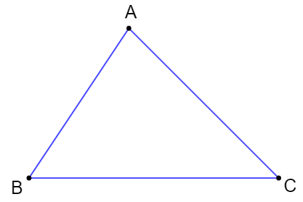
Ví dụ: Cho tam giác ABC như hình dưới đây:

Ta suy ra được các hệ thức sau:

AB < AC + BC

AC < AB + BC

BC < AC + AB

Ba hệ thức phai trên được gọi là các bất đẳng thức tam giác.

2. Quan hệ giữa ba cạnh của một tam giác

Từ định lí trên, ta suy ra được tinh chất sau:

Tính chất: Trong một tam giác, độ dài của một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại.

Ví dụ: Cho tam giác ABC như hình dưới đây:

Ta suy ra được các hệ thức sau:

AB > AC − BC

AC > AB − BC

BC > AC – AB

Nhận xét: Với a, b, c là độ dài ba cạnh tùy ý của một tam giác thì từ định lí và tinh chất nêu trên ta có:

b – c < a < b + c

Chú ý: Để kiểm tra ba độ dài có là ba cạnh của một tam giác hay không, ta chỉ cần so sanh độ dài lớn nhất có nhỏ hơn tổng hai độ dài còn lại hoặc độ dài nhỏ nhất có lớn hơn hiệu hai độ dài còn lại hay không.

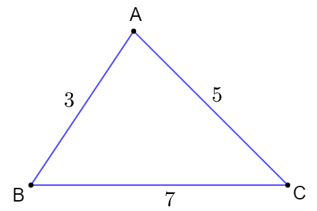
Ví dụ: Cho 3 điểm phân biệt A, B, C với độ dài các đoạn thẳng như sau: AB = 3, AC = 5, BC = 7. Hỏi AB, AC, BC có là ba cạnh của một tam giác hay không?

Để kiểm tra xem AB, AC, BC có là ba cạnh của một tam giác hay không ta có thể chứng minh theo hai cách:

+ Cách 1: Ta so sánh cạnh lớn nhất là BC = 7 với tổng hai cạnh còn lại.

Vì: BC < AB + AC (7 < 3 + 5) nên suy ra AB, AC, BC có là ba cạnh của một tam giác.

+ Cách 2: Ta so sánh cạnh nhỏ nhất AB = 3 với hiệu hai cạnh còn lại.

Vì AB > BC – AC (3 > 7 – 5) nên suy ra AB, AC, BC có là ba cạnh của một tam giác.

Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 71

Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Luyện tập chung trang 83

Bài tập cuối chương 9