Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 18 Tập 1 Kết nối tri thức

    Với giải bài tập Toán lớp 7 trang 18 Tập 1 trong Bài 3: Lũy thừa với số mũ tự nhiên của một số hữu tỉ sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 18 Tập 1.

    1 1,264 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 18 Tập 1

    Luyện tập 3 trang 18 Toán 7 Tập 1:

    Viết kết quả của các phép tính sau dưới dạng lũy thừa.

    a) (–2)3.( –2)4;               

    b) (0,25)7 : (0,25)3.

    Lời giải:

    a) Dạng luỹ thừa của phép tính (–2)3.( –2)4 là: (–2)3.( –2)4 = (–2)3+4 = (–2)7.

    b) Dạng luỹ thừa của phép tính (0,25)7 : (0,25)3 là: (0,25)7 : (0,25)3 = (0,25)7 – 3 = (0,25)4. 

    HĐ 5 trang 18 Toán 7 Tập 1:

    Viết số 223 dưới dạng lũy thừa cơ số 2 và số −322 dưới dạng lũy thừa cơ số –3.

    Lời giải:

    Số 223 được viết dưới dạng lũy thừa cơ số 2 như sau:

    223 = 22. 22. 22 = 22+2+2 = 26.

    Số −322 được viết dưới dạng lũy thừa cơ số –3 như sau:

    −322 = (–3)2. (–3)2 = (–3)2+2 = (–3)4. 

    Luyện tập 4 trang 18 Toán 7 Tập 1:

    Viết các số 148; 183 dưới dạng lũy thừa cơ số 12

    Lời giải:

    Các số 148; 183 được viết dưới dạng lũy thừa cơ số 12 như sau:

    148=1.12.28=12.128=1228=122.8=1216.

    183=1.12.43=1.1.12.2.23=13233=1233=123.3=129.

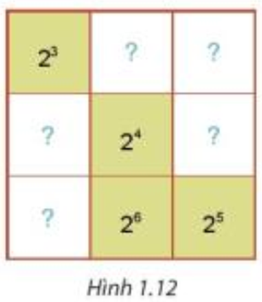
    Thử thách nhỏ trang 18 Toán 7 Tập 1:

    Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết tích các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.

    Tài liệu VietJack

    Lời giải:

    Đặt các ô lần lượt là a, b, c, d, e như hình sau:

    Tài liệu VietJack

    Theo đề bài, tích các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo là bằng nhau nên tích các lũy thừa trên mỗi hàng, mỗi cột, mỗi đường chéo đều có giá trị bằng tích của đường chéo chứa các ô số đã có sẵn là: 23.24.25 = 23+4+5 = 212.

    +) Tích các số của cột 2 là: a.24.26 = a.210 có giá trị bằng 212 nên ta có a.210 = 212.

    Suy ra a = 212 : 210 = 212 – 10 = 22.

    +) Tích các số của hàng 1 là: 23.a.b hay 23.22.b = 23+2.b = 25.b có giá trị bằng 212 nên ta có 25.b = 212.

    Suy ra b = 212 : 25 = 212 – 5 = 27.

    +) Tích các số của hàng 3 là: e.26.25 = e.211 có giá trị bằng  212 nên ta có e.211 = 212

    Suy ra e = 212 : 211 = 212 – 11 = 21.

    +) Tích các số của cột 1 là: 23.c.e hay 23.c.21 = c.23+1 = c.24 có giá trị bằng 212 nên ta có c.24 = 212.

    Suy ra c = 212 : 24 = 212 – 4 = 28.

    +) Tích các số của hàng 2 là: c.24.d hay 28.24.d = 28+4.d = 212.d có giá trị bằng 212 nên ta có 212.d = 212.

    Suy ra d = 212 : 212 = 212 – 12 = 20.

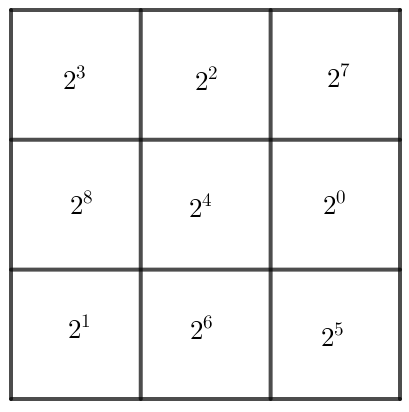
    Ta có bảng như sau:

    Tài liệu VietJack 

     

     

     

     

     

    Bài 1.18 trang 18 Toán 7 Tập 1: Viết các số 125; 3 125 dưới dạng lũy thừa của 5.

    Lời giải:

    Ta có: 125 = 5.25 = 5.5.5 = 53.

    Vậy số 125 được viết dưới dạng luỹ thừa của 5 là 53.

    Ta có: 3 125 = 5.625 = 5.5.125 = 52.53 = 52+3 = 55.

    Vậy số 3 125 được viết dưới dạng luỹ thừa của 5 là 55. 

    Bài 1.19 trang 18 Toán 7 Tập 1: Viết các số 195;1277 dưới dạng lũy thừa cơ số 13

    Lời giải:

    Có: 195=1.13.35=12325=1325=132.5=1310.

    Vậy số 195 được viết dưới dạng luỹ thừa cơ số 13 là 1310.

    Có: 1277=1.1.13.3.37=13337=1337=133.7=1321.

    Vậy số 1277 được viết dưới dạng luỹ thừa cơ số 13 là 1321. 

    Bài 1.20 trang 18 Toán 7 Tập 1: Thay mỗi dấu “?” bởi một lũy thừa của 3, biết rằng từ ô thứ ba, lũy thừa cần tìm là tích của hai lũy thừa ở hai ô liền trước.

    30

    31

    ?

    ?

    ?

    ?

    ?

    Lời giải:

    Theo quy tắc trên của đề bài: từ ô thứ ba, lũy thừa cần tìm là tích của hai lũy thừa ở hai ô liền trước nên ta có:

    Giá trị của ô thứ ba là tích của ô thứ nhất và ô thứ hai: 30.31 = 30+1 = 31;

    Giá trị của ô thứ tư là tích của ô thứ hai và ô thứ ba: 31.31 = 31+1 = 32;

    Giá trị của ô thứ năm là tích của ô thứ ba và ô thứ tư: 31.32 = 31+2 = 33;

    Giá trị của ô thứ sáu là tích của ô thứ tư và ô thứ năm: 32.33 = 32+3 = 35;

    Giá trị của ô thứ bảy là tích của ô thứ năm và ô thứ sáu: 33.35 = 33+5 = 38.

    Khi đó ta có bảng sau:

    30

    31

    31

    32

    33

    35

    38

    Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giải Toán 7 trang 16 Tập 1

    Giải Toán 7 trang 17 Tập 1

    Giải Toán 7 trang 19 Tập 1

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,264 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: