Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 81 Tập 1 Kết nối tri thức

    Với giải bài tập Toán lớp 7 trang 81 Tập 1 trong Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 81 Tập 1.

    1 467 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 81 Tập 1

    HĐ 1 trang 81 Toán 7 Tập 1: Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.

    a) Chứng minh rằng ΔABD=ΔACD theo trường hợp cạnh – cạnh – cạnh.

    b) Hai góc B và C của tam giác ABC có bằng nhau không?

    Tài liệu VietJack

    Lời giải:

    GT

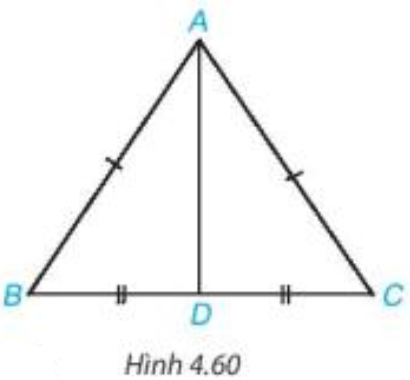
    ΔABC cân tại A, D là trung điểm của BC.

    KL

    a) ΔABD=ΔACD(c.c.c);

    b) B^ và C^ của tam giác ABC có bằng nhau không?

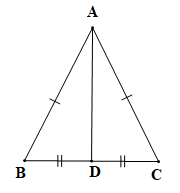
    Tài liệu VietJack

    Chứng minh (hình vẽ trên):

    a) Tam giác ABC cân tại A (theo giả thiết) nên ta có AB = AC (định nghĩa tam giác cân).

    Xét tam giác ABD và tam giác ACD có:

    AB = AC (chứng minh trên);

    BD = CD (do D là trung điểm của BC);

    AD là cạnh chung.

    Vậy ΔABD=ΔACD (c.c.c).

    b) Từ ΔABD=ΔACD (chứng minh câu a) suy ra ABD^=ACD^ (hai góc tương ứng).

    Hay B^=C^.

    Vậy góc B^ và C^ của tam giác ABC cân tại A bằng nhau. 

    HĐ 2 trang 81 Toán 7 Tập 1:

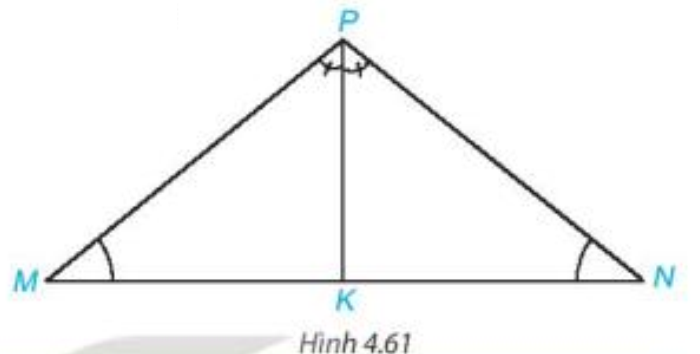
    Cho tam giác MNP có M^=N^. Vẽ tia phân giác PK của góc MPN (K∈MN).

    Chứng minh rằng:

    a) MKP^=NKP^;                                

    b) ΔMPK=ΔNPK;

    c) Tam giác MNP có cân tại P không?

    Tài liệu VietJack

    Lời giải:

    GT

    ΔMNP, M^=N^;

    PK là tia phân giác của góc MPN.

    KL

    a) MKP^=NKP^; 

    b) ΔMPK=ΔNPK;

    c) Tam giác MNP có cân tại P không?

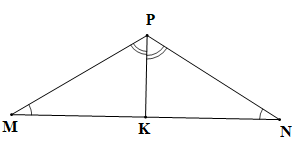
    Tài liệu VietJack

    Chứng minh (hình vẽ trên):

    a) PK là tia phân giác của góc MPN (theo giả thiết) nên MPK^=NPK^ (tính chất tia phân giác của một góc).

    Tam giác MPK có NKP^ là góc ngoài của tam giác tại đỉnh K nên ta có NKP^=MPK^+M^.

    Tam giác NPK có MKP^ là góc ngoài của tam giác tại đỉnh K nên ta có MKP^=NPK^+N^.

    Mà MPK^=NPK^ (chứng minh trên) và M^=N^ (theo giả thiết).

    Do đó MKP^=NKP^.

    b) Xét tam giác MPK và tam giác NPK có:

    MPK^=NPK^ (chứng minh ở câu a);

    PK là cạnh chung;

    MKP^=NKP^ (chứng minh ở câu a).

    Vậy ΔMPK=ΔNPK (g.c.g).

    c) Từ ΔMPK=ΔNPK (chứng minh ở câu b) suy ra MP = NP (hai cạnh tương ứng).

    Do đó tam giác MNP cân tại P (định nghĩa tam giác cân).

    Vậy tam giác MNP cân tại P.

    Luyện tập 1 trang 81 Toán 7 Tập 1: Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.

    Tài liệu VietJack

    Lời giải:

    GT

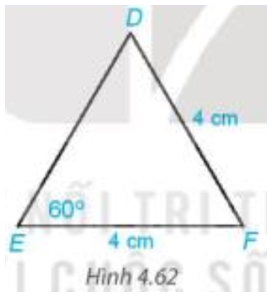
    ΔDEF, EF = DF = 4 cm, E^=60°.

    KL

    Tính số đo D^,F^ và độ dài cạnh DE.

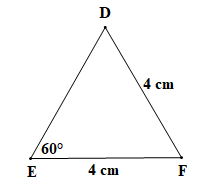
    Tài liệu VietJack

    Tam giác DEF có EF = DF = 4 cm (theo giả thiết) nên tam giác DEF cân tại F (định nghĩa tam giác cân).

    Do đó D^=E^ (tính chất tam giác cân).

    Mà E^=60° (theo giả thiết) nên D^=60°.

    Tam giác DEF có D^=60°, E^=60°, áp dụng định lí tổng ba góc trong một tam giác ta có D^+E^+F^=180°.

    Suy ra F^=180°−D^−E^ 

    Hay F^=180°−60°−60°=60°. 

    Khi đó ta có E^=F^=60°.

    Suy ra tam giác DEF cân tại D (dấu hiệu nhận biết tam giác cân).

    Do đó DE = DF (định nghĩa tam giác cân).

    Mà DF = 4 cm (theo giả thiết).

    Vậy DE = 4 cm. 

    Thử thách nhỏ trang 81 Toán 7 Tập 1:

    Một tam giác có gì đặc biệt nếu thỏa mãn một trong các điều kiện sau:

    a) Tam giác có ba góc bằng nhau.

    b) Tam giác cân có một góc bằng 60o.

    Lời giải:

    a)

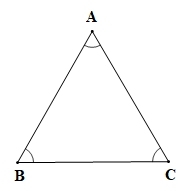
    Tài liệu VietJack

    Áp dụng định lí tổng ba góc trong tam giác cho tam giác ABC ta có A^+B^+C^=180°.

    Mà A^=B^=C^ (theo giả thiết);

    Suy ra A^+A^+A^=180° hay 3.A^=180°.

    Do đó A^=60°. 

    Khi đó A^=B^=C^=60°.

    Tam giác ABC có ba góc bằng nhau và cùng bằng 60° nên là tam giác đều.

    b) +) Tam giác DEF cân tại D có E^=60°. 

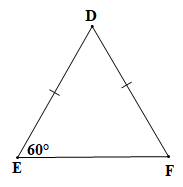
    Tài liệu VietJack

    Tam giác DEF cân tại D (theo giả thiết) nên E^=F^ (tính chất tam giác cân).

    Mà E^=60°, do đó F^=60°. 

    Tam giác DEF có E^=60°, F^=60°, áp dụng định lí tổng ba góc trong một tam giác ta có D^+E^+F^=180°.

    Suy ra D^=180°−E^−F^ 

    Hay D^=180°−60°−60°=60°. 

    Khi đó ta có D^=E^=F^=60°.

    Tam giác DEF có ba góc bằng nhau và cùng bằng 60° nên là tam giác đều.

    +) Tam giác MNP cân tại M có M^=60°. 

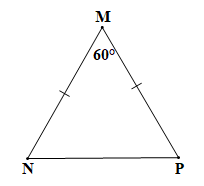
    Tài liệu VietJack

    Tam giác MNP cân tại M (theo giả thiết) nên N^=P^ (tính chất tam giác cân).

    Tam giác MNP có M^=60°, N^=P^, áp dụng định lí tổng ba góc trong một tam giác ta có M^+N^+P^=180°.

    Suy ra 60°+N^+N^=180° 

    Hay 2.N^=180°−60°

     2.N^=120°

    N^=60°.

    Khi đó M^=N^=P^=60°.

    Tam giác MNP có ba góc bằng nhau và cùng bằng 60° nên là tam giác đều. 

    HĐ 3 trang 81 – 82 Toán 7 Tập 1: Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB.

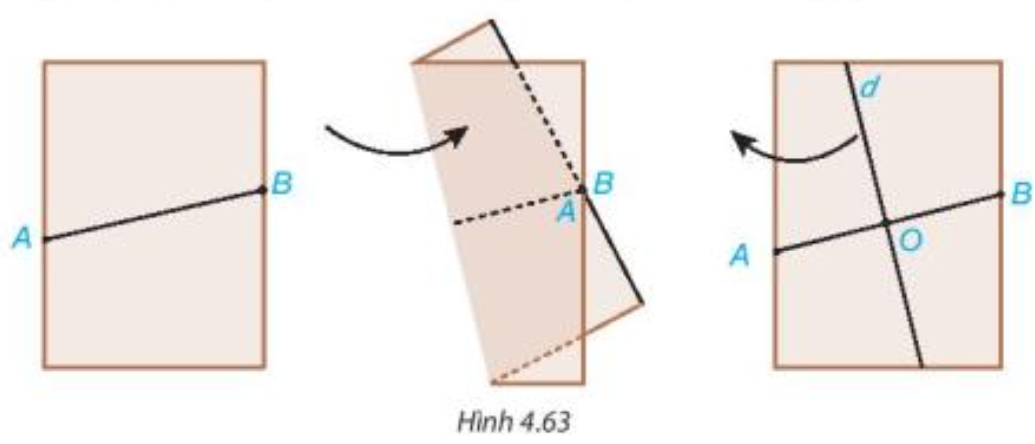
    Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau.

    Mở mảnh giấy ra, kẻ đường thẳng d theo nếp gấp.

    a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?

    b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?

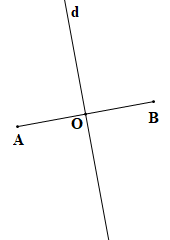
    Tài liệu VietJack

    Lời giải:

    Tài liệu VietJack

    Mảnh giấy sau khi gấp được mô tả như hình vẽ trên.             

    a) Mảnh giấy được gấp sao cho điểm A trùng với điểm B, O là giao điểm của đường thẳng d và AB, khi đó đường thẳng d chia đoạn thẳng AB thành hai đoạn bằng nhau, tức là OA = OB.

    Do đó O là trung điểm của đoạn thẳng AB.

    b) Dùng thước đo góc ta thấy góc dOB có số đo bằng 90° nên d⊥AB. 

    Vậy đường thẳng d vuông góc với AB.

    Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giải Toán 7 trang 80 Tập 1

    Giải Toán 7 trang 82 Tập 1

    Giải Toán 7 trang 83 Tập 1

    Giải Toán 7 trang 84 Tập 1

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 467 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: