Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 73 Tập 1 Kết nối tri thức

    Với giải bài tập Toán lớp 7 trang 73 Tập 1 trong Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang  Tập 1.

    1 1,678 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 73 Tập 1

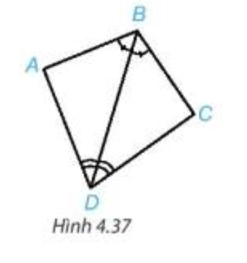
    Luyện tập 2 trang 73 Toán 7 Tập 1: Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.

    Tài liệu VietJack

    Lời giải:

    GT

    ΔABD,ΔCBD; 

    ADB^=CDB^,ABD^=CBD^.    

    KL

    ΔABD=ΔCBD.

    Tài liệu VietJack 

    Chứng minh (hình vẽ trên):

    Xét tam giác ABD và tam giác CBD có:

    ADB^=CDB^ (theo giả thiết);

    DB là cạnh chung;

    ABD^=CBD^ (theo giả thiết).

    Vậy ΔABD=ΔCBD (g.c.g).

    Thử thách nhỏ trang 73 Toán 7 Tập 1: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?

    Tài liệu VietJack

    Lời giải:

    GT

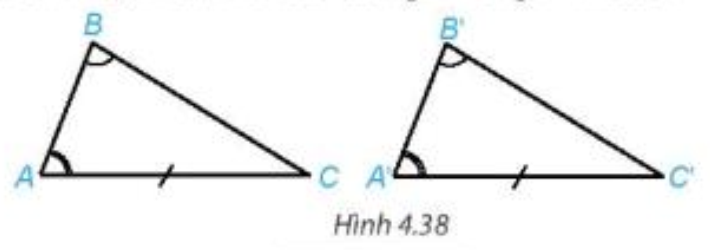
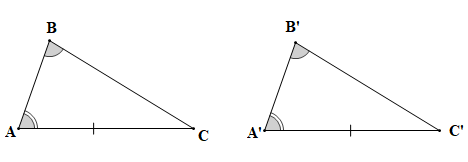
    ΔABD,ΔA'B'C'; ABC^=A'B'C'^, BAC^=B'A'C'^, AC = A'C'.

    KL

    ΔABC và ΔA'B'C' có bằng nhau không?

    Tài liệu VietJack

    Chứng minh (hình vẽ trên):

    Áp dụng định lí tổng ba góc trong một tam giác cho tam giác ABC và tam giác A'B'C' ta có:

    Trong tam giác ABC: BAC^+ABC^+BCA^=180°, suy ra BCA^=180°−BAC^+ABC^

    Trong tam giác A'B'C': B'A'C'^+A'B'C'^+B'C'A'^=180°,

    Suy ra B'C'A'^=180°−B'A'C'^+A'B'C'^

    Mà ABC^=A'B'C'^, BAC^=B'A'C'^ (theo giả thiết).

    Do đó BAC^+ABC^=B'A'C'^+A'B'C'^.

    Nên 180°−BAC^+ABC^=180°−B'A'C'^+A'B'C'^

    Hay BCA^=B'C'A'^.

    Xét tam giác ABC và tam giác A'B'C' có:

    BAC^=B'A'C'^ (theo giả thiết);

    AC = A'C' (theo giả thiết);

    BCA^=B'C'A'^(chứng minh trên).

    Vậy ΔABC=ΔA'B'C' (g.c.g). 

    Vậy bạn Lan nói đúng.

    Bài 4.12 trang 73 Toán 7 Tập 1: Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.

    Tài liệu VietJack

    Lời giải:

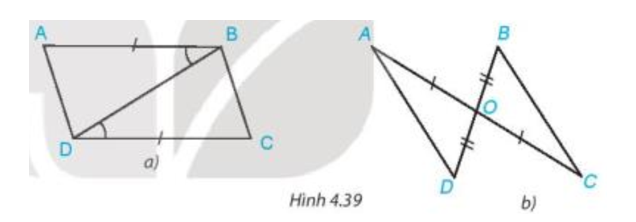
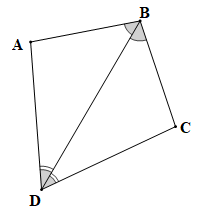
    +) Hình 4.39 a)

    GT

    ΔABD,ΔCDB; 

    ABD^=CDB^, AB = CD. 

    KL

    Chỉ ra một cặp tam giác bằng nhau. Giải thích vì sao chúng bằng nhau.

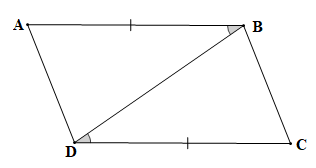
    Tài liệu VietJack

    Xét tam giác ABD và tam giác CDB có:

    AB = CD (theo giả thiết);

    ABD^=CDB^ (theo giả thiết);

    BD là cạnh chung.

    Vậy ΔABD=ΔCDB (c.g.c).

    +) Hình 4.39 b)

    GT

    ΔOAD,ΔOCB;OA = OC, OD = OB.

    KL

    Chỉ ra một cặp tam giác bằng nhau. Giải thích vì sao chúng bằng nhau.

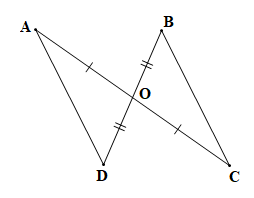
     Tài liệu VietJack

    Xét tam giác OAD và tam giác OCB có:

    OA = OC (theo giả thiết);

    AOD^=COB^ (hai góc đối đỉnh);

    OD = OB (theo giả thiết).

    Vậy ΔOAD=ΔOCB (c.g.c).  

    Bài 4.13 trang 73 Toán 7 Tập 1: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

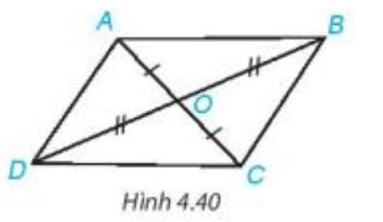
    a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.

    b) Chứng minh rằng ΔDAB=ΔBCD.

    Tài liệu VietJack

    Lời giải:

    GT

    O∈AC,O∈BD, OA = OC, OB = OD.

    KL

    a) Tìm hai cặp tam giác có chung đỉnh O bằng nhau;

    b) Chứng minh ΔDAB=ΔBCD. 

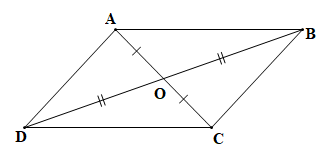
    Tài liệu VietJack

    a) Hai cặp tam giác có chung đỉnh O bằng nhau là:

     +) Tam giác OAB và tam giác OCD

    Giải thích:

    OA = OC (giải thuyết)

    OB = OD (giải thuyết)

    AOB^=COD^ (hai góc đối đỉnh)

    Do đó, ΔOAB=ΔOCD (c – g – c)

    +) Tam giác OAD và tam giác OCB.

    Giải thích:

    OA = OC (giải thuyết)

    OD = OB (giải thuyết)

    AOD^=COB^ (hai góc đối đỉnh)

    Do đó, ΔOAD=ΔOCB (c – g – c)

    b) ΔOAB=ΔOCD (Chứng minh ở câu a) nên ABO^=CDO^ (hai góc tương ứng) hay ABD^=CDB^. 

    ΔOAD=ΔOCB(Chứng minh ở câu a) nên ADO^=CBO^ (hai góc tương ứng) hay ADB^=CBD^. 

    +) Xét tam giác DAB và tam giác BCD có:

    ABD^=CDB^ (chứng minh trên);

    BD là cạnh chung;

    ADB^=CBD^ (chứng minh trên).

    Vậy ΔDAB=ΔBCD (g.c.g). 

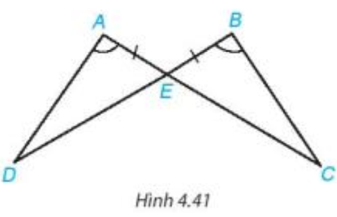
    Bài 4.14 trang 73 Toán 7 Tập 1: Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.

    Tài liệu VietJack

    Lời giải:

    GT

    ΔADE,ΔBCE;AE = BE, DAE^=CBE^.  

    KL

    ΔADE=ΔBCE.

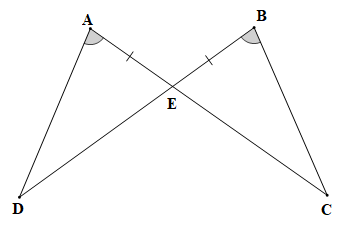
    Tài liệu VietJack

    Chứng minh (hình vẽ trên):

    Xét tam giác ADE và tam giác BCE có:

    DAE^=CBE^ (theo giả thiết);

    AE = BE (theo giả thiết);

    AED^=BEC^ (hai góc đối đỉnh).

    Vậy ΔADE=ΔBCE (g.c.g). 

    Bài 4.15 trang 73 Toán 7 Tập 1: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:

    a) ΔABE=ΔDCE;                             

    b) EG = EH.

    Tài liệu VietJack

    Lời giải:

    GT

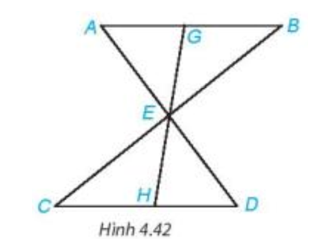
    AB = CD, AB // CD;

    E là giao điểm của AD và BC;

    G∈AB,H∈CD;

    G, E, H thẳng hàng.

    KL

    a) ΔABE=ΔDCE;

    b) EG = EH.

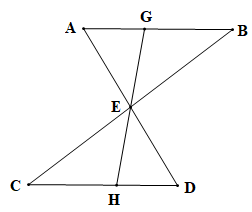
     Tài liệu VietJack

    a) Từ AB // CD (theo giả thiết) suy ra DAB^=ADC^ (hai góc so le trong) và ABC^=DCB^ (hai góc so le trong).

    Hay EAB^=EDC^ và ABE^=DCE^.

    Xét tam giác ABE và tam giác DCE có:

    EAB^=EDC^ (chứng minh trên);

    AB = DC (theo giả thiết);

    ABE^=DCE^ (chứng minh trên).

    Vậy ΔABE=ΔDCE (g.c.g).

    b) Từ ΔABE=ΔDCE(chứng minh câu a) suy ra AE = DE (hai cạnh tương ứng).

    Xét tam giác AEG và tam giác DEH có:

    EAG^=EDH^ (do EAB^=EDC^);

    AE = DE (chứng minh trên);

    AEG^=DEH^ (hai góc đối đỉnh).

    Vậy ΔAEG=ΔDEH (g.c.g).

    Suy ra EG = EH (hai cạnh tương ứng).

    Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giải Toán 7 trang 70 Tập 1

    Giải Toán 7 trang 71 Tập 1

    Giải Toán 7 trang 72 Tập 1

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,678 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: