Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 86 Tập 1 Kết nối tri thức

    Với giải bài tập Toán lớp 7 trang 86 Tập 1 trong Luyện tập chung trang 85, trang 86 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 86 Tập 1.

    1 515 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 86 Tập 1

    Bài 4.29 trang 86 Toán 7 Tập 1: Cho Hình 4.73. Hãy tìm số đo x, y của các góc và độ dài a, b của các đoạn thẳng trên hình vẽ.

    Tài liệu VietJack

    Lời giải:

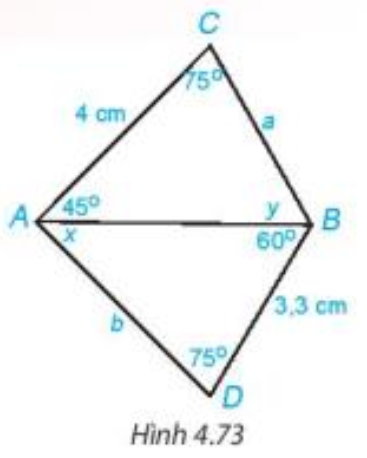
    GT

    ΔABC,ΔABD, AC = 4 cm, BD = 3,3 cm;

    BAC^=45°,ABD^=60°,ACB^=75°,ADB^=75°. 

    KL

    Tìm x, y và tính a, b.

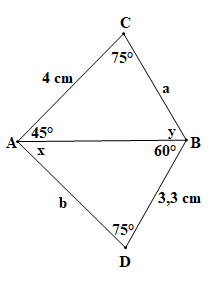
    Tài liệu VietJack

    +) Xét tam giác ABD có ABD^=60°,ADB^=75°, theo định lí tổng ba góc trong một tam giác ta có BAD^+ABD^+ADB^=180°.

    Suy ra BAD^=180°−ABD^−ADB^

    Hay x = 180° – 60° – 75°

     x = 45°.

    Xét tam giác ABC có BAC^=45°,ACB^=75°, theo định lí tổng ba góc trong một tam giác ta có BAC^+ABC^+ACB^=180°.

    Suy ra ABC^=180°−BAC^−ACB^

    Hay y = 180° – 45° – 75°

     y = 60°.

    +) Xét tam giác ABC và tam giác ABD có:

    BAC^=BAD^ (cùng có số đo bằng 45°);

    AB là cạnh chung;

    ABC^=ABD^ (cùng có số đo bằng 60°).

    Vậy ΔABC=ΔABD (g.c.g).

    Suy ra BC = BD (hai cạnh tương ứng) và AC = AD (hai cạnh tương ứng).

    Mà BD = 3,3 cm và AC = 4 cm.

    Do đó a = BC = 3,3 cm và b = AD = 4 cm.

    Vậy  x = 45°,  y = 60°, a = 3,3 cm và b = 4 cm.  

    Bài 4.30 trang 86 Toán 7 Tập 1: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng:

    a) ΔOAN=ΔOBM;

    b) ΔAMN=ΔBNM.

    Lời giải:

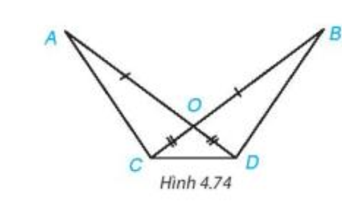
    GT

    xOy^, A,M∈Ox;B,N∈Oy;

    OA = OB, OM = ON, OA > OM.

    KL

    a) ΔOAN=ΔOBM; 

    b) ΔAMN=ΔBNM.

    Tài liệu VietJack

    a) Xét tam giác OAN và tam giác OBM có:

    OA = OB (theo giả thiết);

    AOB^ là góc chung;

    ON = OM (theo giả thiết).

    Vậy ΔOAN=ΔOBM (c.g.c).

    b) Do B, N cùng nằm trên tia Oy, OA = OB, OM = ON và OA > OM (theo giả thiết) nên OB > ON, khi đó OB = ON + NB suy ra NB = OB – ON.

    Do A, M cùng nằm trên tia Ox, OA > OM (theo giả thiết) nên OA = OM + MA suy ra MA = OA – OM.

    Lại có OA = OB, OM = ON (theo giả thiết) nên OA – OM = OB – ON.

    Hay MA = NB.

    Từ ΔOAN=ΔOBM (chứng minh ở câu a) suy ra AN = BM (hai cạnh tương ứng).

    Xét tam giác AMN và tam giác BNM có:

    AN = BM (chứng minh trên);

    MN là cạnh chung;

    MA = NB (chứng minh trên).

    Vậy ΔAMN=ΔBNM(c.g.c).

    Bài 4.31 trang 86 Toán 7 Tập 1: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:

    a) AC = BD;

    b) ΔACD=ΔBDC.

    Tài liệu VietJack

    Lời giải:

    GT

    OA = OB, OC = OD.

    KL

    a) AC = BD;

    b) ΔACD=ΔBDC.

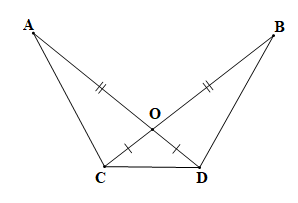
    Tài liệu VietJack

    a) Xét tam giác OAC và tam giác OBD có:

    OA = OB (theo giả thiết);

    AOC^=BOD^ (hai góc đối đỉnh);

    OC = OD (theo giả thiết).

    Vậy ΔOAC=ΔOBD (c.g.c).

    Suy ra AC = BD (hai cạnh tương ứng).

    b) Ta có AD = AO + OD và BC = BO + OC.

    Mà OA = OB, OC = OD (theo giả thiết) nên AO + OD = BO + OC hay AD = BC.

    Xét tam giác ACD và tam giác BDC có:

    AC = BD (chứng minh ở câu a);

    AD = BC (chứng minh trên);

    CD là cạnh chung.

    Vậy ΔACD=ΔBDC (c.c.c). 

    Bài 4.32 trang 86 Toán 7 Tập 1: Cho tam giác MBC vuông tại M có B^=60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

    Lời giải:

    GT

    ΔMBC vuông tại M, B^=60°, MA = MB.

    KL

    Tam giác ABC là tam giác đều.

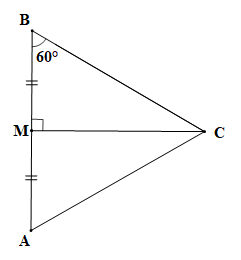
    Tài liệu VietJack

    Xét tam giác MBC (vuông tại M) và tam giác MAC (vuông tại M) có:

    MB = MA (theo giả thiết);

    MC là cạnh chung.

    Vậy ΔMBC=ΔMAC (hai cạnh góc vuông).

    Suy ra B^=A^ (hai góc tương ứng)

    Mà B^=60° nên B^=A^=60°.

    Tam giác ABC có B^=A^=60°, theo định lí tổng ba góc trong một tam giác ta có A^+B^+C^=180°

    Suy ra C^=180°−A^−B^ hay C^=180°−60°−60°=60°. 

    Do đó A^=B^=C^=60° suy ra tam giác ABC đều.

    Vậy tam giác ABC đều. 

    Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

    Bài tập cuối chương 4 trang 87

    Bài 17: Thu thập và phân loại dữ liệu

    Bài 18: Biểu đồ hình quạt tròn

    Bài 19: Biểu đồ đoạn thẳng

    Luyện tập chung

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 515 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: