Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 47 Tập 2 Chân trời sáng tạo

    Với giải bài tập Toán lớp 7 trang 47 Tập 2 trong Bài 1: Góc và cạnh của một tam giác sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 47 Tập 2.

    1 584 18/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 47 Tập 2

    Bài 2 trang 47 Toán 7 Tập 2:

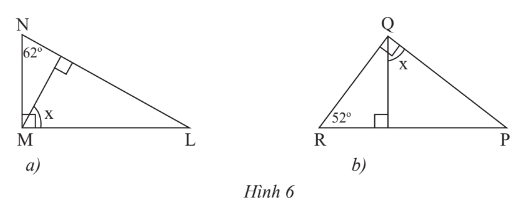
    Tính số đo x của góc trong Hình 6.

    Giải Toán 7 Bài 1 (Chân trời sáng tạo): Góc và cạnh của một tam giác (ảnh 1) 

    Lời giải:

    * Xét Hình 6a:

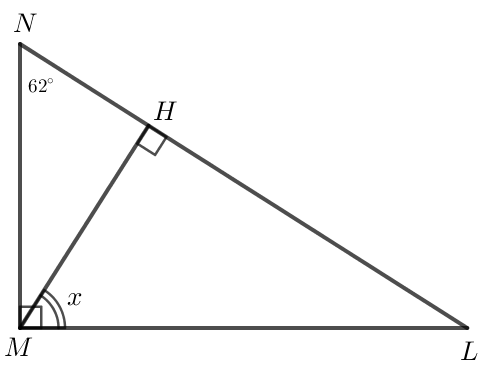
    Giải Toán 7 Bài 1 (Chân trời sáng tạo): Góc và cạnh của một tam giác (ảnh 1) 

    Kẻ MH vuông góc với LN tại H.

    Xét ∆NML vuông tại M có:

    N^+L^=90° (trong một tam giác vuông, tổng hai góc nhọn bằng 90°)

    Do đó L^=90°−N^ = 90° - 62° = 28°.

    Xét ∆MLH vuông tại H có:

    HML^ + L^ = 90° (trong một tam giác vuông, tổng hai góc nhọn bằng 90°)

    Hay  x + L^ = 90°.

    Do đó x = 90° - L^ = 90° - 28° = 62°.

    * Xét Hình 6b:

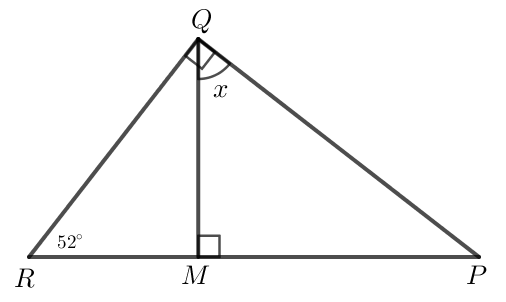
    Giải Toán 7 Bài 1 (Chân trời sáng tạo): Góc và cạnh của một tam giác (ảnh 1) 

    Kẻ QM vuông góc với RP tại M.

    Xét ∆QRP vuông tại Q có

    R^+P^=90° (trong một tam giác vuông, tổng hai góc nhọn bằng 90°)

    Do đó P^=90°−R^ = 90° - 52° = 38°.

    Xét ∆QMP vuông tại M có:

    MQP^+P^=90° (trong một tam giác vuông, tổng hai góc nhọn bằng 90°)

    Hay x + P^ = 90°.

    Do đó x = 90° - P^ = 90° - 38° = 52°.

    Vậy trong Hình 6a: x = 62°; Hình 6b: x = 52°.

    Bài 3 trang 47 Toán 7 Tập 2:

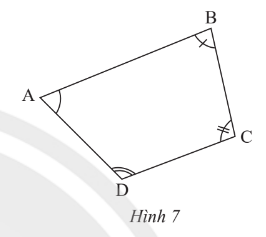
    Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc A^,  B^,  C^,  D^.

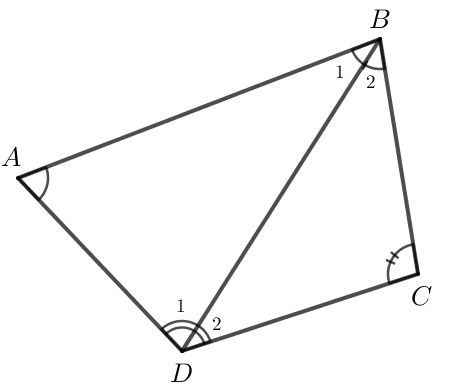
    Giải Toán 7 Bài 1 (Chân trời sáng tạo): Góc và cạnh của một tam giác (ảnh 1) 

    Lời giải:

    Giải Toán 7 Bài 1 (Chân trời sáng tạo): Góc và cạnh của một tam giác (ảnh 1) 

    Nối BD. Khi đó, tứ giác ABCD được chia thành hai tam giác ABD và BCD.

    Xét ∆ABD có A^+B^1+D^1=180° (định lí về tổng số đo ba góc của tam giác)

    Xét ∆BCD có B^2+C^+D^2=180° (định lí về tổng số đo ba góc của tam giác)

    Do đó A^+B^1+D^1+B^2+C^+D^2 = 180° + 180° = 360°.

    Hay A^+B^1+B^2+C^+D^1+D^2=360°.

    Mà ABC^=B^1+B^2;  ADC^=D^1+D^2

    Suy ra A^+ABC^+C^+ADC^=360°. 

    Vậy tổng số đo bốn góc A^,  B^,  C^,  D^ trong Hình 7 bằng 360°.

    Bài 4 trang 47 Toán 7 Tập 2:

    Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

    a) 4 cm, 5 cm, 7 cm;

    b) 2 cm, 4 cm, 6 cm;

    c) 3 cm, 4 cm, 8 cm.

    Lời giải:

    a) Ta có: 4 + 5 = 9 > 7, thỏa mãn bất đẳng thức tam giác, nên bộ ba độ dài 4 cm, 5 cm, 7 cm là độ dài ba cạnh của tam giác.

    b) Ta có 2 + 4 = 6, không thỏa mãn bất đẳng thức tam giác, nên bộ ba độ dài 2 cm, 4 cm, 6 cm không phải là độ dài ba cạnh của tam giác.

    c) Ta thấy 3 + 4 = 7 < 8, không thỏa mãn bất đẳng thức tam giác, nên bộ ba độ dài 3 cm, 4 cm, 8 cm không phải là độ dài ba cạnh của tam giác.

    Bài 5 trang 47 Toán 7 Tập 2:

    Cho tam giác ABC có BC = 1 cm, AB = 4 cm. Tính độ dài cạnh AC (theo đơn vị cm), biết rằng độ dài này là một số nguyên.

    Lời giải:

    Ta có: AB - BC = 4 – 1 = 3 (cm); AB + BC = 4 + 1 = 5 (cm).

    Xét DABC, theo bất đẳng thức tam giác, ta có:

    AB - BC < AC < AB + BC.

    Do đó 3 cm < AC < 5 cm.

    Mà độ dài cạnh AC là một số nguyên nên AC = 4 cm.

    Vậy AC = 4 cm.

    Bài 6 trang 47 Toán 7 Tập 2:

    Trong một trường học, người ta đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = 15 m, AB = 45 m.

    a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì tại khu vực B có nhận được tín hiệu không? Vì sao?

    b) Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60 m.

    Lời giải:

    a) Ta có: AB - AC = 45 - 15 = 30 (m).

    Xét DABC, theo bất đẳng thức tam giác, ta có:

    BC > AB - AC

    Hay BC > 30 (m), tức là khoảng cách từ C đến B lớn hơn 30 m.

    Vậy nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì tại khu vực B không nhận được tín hiệu.

    b) Ta có: AB + AC = 15 + 15 = 60 (m).

    Xét DABC, theo bất đẳng thức tam giác, ta có:

    BC < AB + AC

    Hay BC < 60 (m), tức là khoảng cách từ C đến B nhỏ hơn 60 m.

    Vậy nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 60 m thì tại khu vực B nhận được tín hiệu.

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Giải Toán 7 trang 44 Tập 2

    Giải Toán 7 trang 45 Tập 2

    Giải Toán 7 trang 46 Tập 2

    Giải Toán 7 trang 47 Tập 2

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Khởi động trang 44 Toán 7 Tập 2: Hãy đo ba góc và ba cạnh của tam giác trong hình bên. - Em có nhận xét gì về tổng số đo của ba góc trong tam giác này...

    Khám phá 1 trang 44 Toán 7 Tập 2: a) Cắt một tấm bìa hình tam giác và tô màu ba góc của nó (Hình 1a). Cắt rời ba góc ra khỏi tam giác rồi đặt ba góc kề nhau...

    Thực hành 1 trang 45 Toán 7 Tập 2: Tìm số đo các góc chưa biết của các tam giác trong Hình 3 và cho biết tam giác nào là tam giác nhọn...

    Khám phá 2 trang 45 Toán 7 Tập 2: Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại...

    Thực hành 2 trang 46 Toán 7 Tập 2: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác? a) 7 cm; 8 cm; 11 cm...

    Vận dụng trang 46 Toán 7 Tập 2: Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5 cm, AC = 3 cm thì cạnh BC...

    Bài 1 trang 46 Toán 7 Tập 2: Tìm số đo các góc chưa biết của các tam giác trong Hình 5...

    Bài 2 trang 47 Toán 7 Tập 2: Tính số đo x của góc trong Hình 6...

    Bài 3 trang 47 Toán 7 Tập 2: Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc A^,  B^,  C^,  D^...

    Bài 4 trang 47 Toán 7 Tập 2: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác? a) 4 cm, 5 cm, 7 cm...

    Bài 5 trang 47 Toán 7 Tập 2: Cho tam giác ABC có BC = 1 cm, AB = 4 cm. Tính độ dài cạnh AC (theo đơn vị cm), biết rằng độ dài này là một số nguyên...

    Bài 6 trang 47 Toán 7 Tập 2: Trong một trường học, người ta đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = 15 m, AB = 45 m...

    Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

    Bài tập cuối chương 7

    Bài 1: Góc và cạnh của một tam giác

    Bài 2: Tam giác bằng nhau

    Bài 3: Tam giác cân

    Bài 4: Đường vuông góc và đường xiên

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 584 18/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: