Toán 7 Bài 1 (Chân trời sáng tạo): Các góc ở vị trí đặc biệt
Với giải bài tập Toán lớp 7 Bài 1: Các góc ở vị trí đặc biệt sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 1
Giải bài tập Toán 7 Bài 1: Tập hợp các số hữu tỉ
Hoạt động khởi động
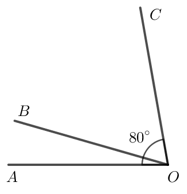
Khởi động trang 69 Toán lớp 7 Tập 1: Thế nào là hai góc kề nhau nhỉ?
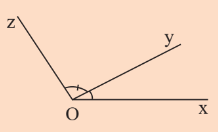
Lời giải:
Sau bài học này chúng ta sẽ trả lời được câu hỏi trên như sau:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
1. Hai góc kề bù
Khám phá 1 trang 69 Toán lớp 7 Tập 1:
a) Quan sát Hình 1 và cho biết hai góc ^xOy và ^yOz có:
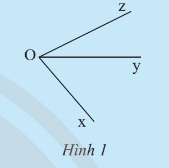
b) Hãy đo các góc ^xOy, ^yOz, ^xOz trong Hình 1 rồi so sánh tổng số đo của ^xOy và ^yOz với ^xOz.
c) Tính tổng số đo của hai góc ^mOn và ^nOp trong Hình 2.
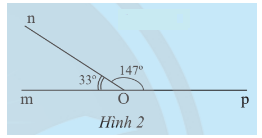
Lời giải:
a) Hai góc ^xOy và ^yOz có cạnh chung là Oy và không có điểm trong chung.
b) Sử dụng thước đo góc, ta đo được ^xOy = 50°, ^yOz = 26°, ^xOz = 76°.
Khi đó ^xOy+^yOz=^xOz.
c) Tổng số đo hai góc ^mOn và ^nOp là: 33o + 147o = 180o.
Thực hành 1 trang 69 Toán lớp 7 Tập 1: Quan sát Hình 5.
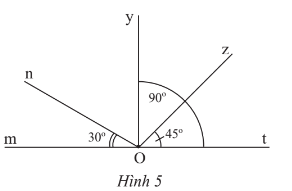
b) Tìm số đo của góc kề bù với ^mOn.
d) Tìm số đo của góc kề bù với ^tOz.
Lời giải:
a) Các góc kề với ^tOz là: ^zOy,^zOn,^zOm.
b) Góc kề bù với ^mOn là ^nOt.
Do ^nOt là góc kề bù với ^mOn nên ^mOn+^nOt=180°.
Do đó hay .
c) Do Oy nằm giữa Ot và On nên
Do đó hay .
d) Góc kề bù với là .
Do là góc kề bù với nên .
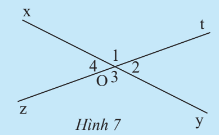
Do đó hay .
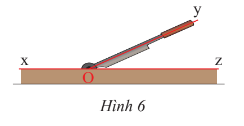
Lời giải:
Hai góc kề bù có trong hình là và .
2. Hai góc đối đỉnh
Lời giải:
Quan hệ về cạnh của và : Ox là tia đối của Oy, Ot là tia đối của Oz.
Quan hệ về đỉnh của và : Hai góc có chung đỉnh O.
Thực hành 2 trang 70 Toán lớp 7 Tập 1:
a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I. Xác định các cặp góc đối đỉnh trên hình vẽ.
Lời giải:
a)
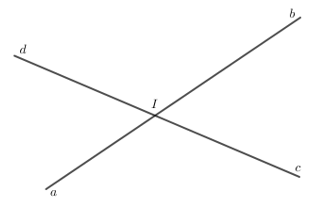
Các cặp góc đối đỉnh: và ; và .
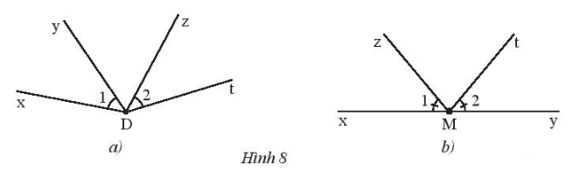
b) Thực hiện theo các bước như sau:
Bước 1. Vẽ góc xOy bất kì.
Bước 2. Vẽ Ot là tia đối của Ox, Oz là tia đối của Oy. Ta thu được góc tOz cần vẽ.
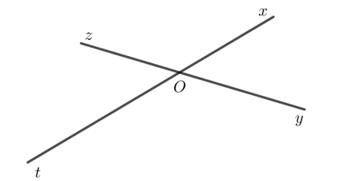
c) - Hai góc và trong Hình 8a không phải hai góc đối đỉnh do mỗi cạnh của không phải tia đối của một cạnh của .
- Hai góc và trong Hình 8b không phải hai góc đối đỉnh do Oz không phải tia đối của Ot.
Lời giải:
Các cặp góc đối đỉnh là: và , và .
3. Tính chất của hai góc đối đỉnh
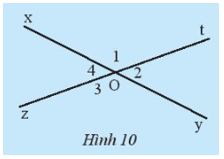
Khám phá 3 trang 71 Toán lớp 7 Tập 1: Quan sát Hình 10.
a) Hãy dùng thước đo góc để đo và . So sánh số đo hai góc đó.
b) Hãy dùng thước đo góc để đo và . So sánh số đo hai góc đó.
Lời giải:
a) Sử dụng thước đo góc ta đo được = 133o; = 133o.
Ta có = .
b) Sử dụng thước đo góc ta đo được = 47o; = 47o.
Ta có =.
Thực hành 3 trang 71 Toán lớp 7 Tập 1: Quan sát Hình 12.
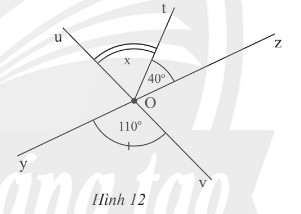
Lời giải:
a) Góc đối đỉnh của là .
b) Do là góc đối đỉnh của nên .
Do đó = 110o.
Vận dụng 3 trang 71 Toán lớp 7 Tập 1: Tìm số đo x của trong Hình 12.
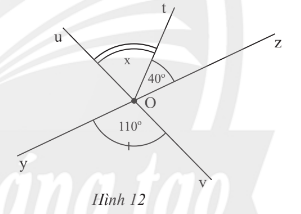
Lời giải:
Ta có: .
Do Ot nằm giữa Ou và Oz nên
Do đó hay
Vậy x = 70o.
Bài tập
Bài 1 trang 72 Toán lớp 7 Tập 1: Quan sát Hình 14.
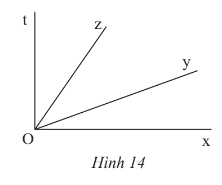
b) Tìm số đo của nếu cho biết .
Lời giải:
a) Các góc kề với là: .
b) Do Oy nằm giữa Ox và Ot nên .
Do đó hay
Do Oz nằm giữa Oy và Ot nên .
Mà nên .
Do đó = 35o.
Vậy = 35o.
Bài 2 trang 72 Toán lớp 7 Tập 1: Cho hai góc kề bù với nhau. Biết . Tính .
Lời giải:
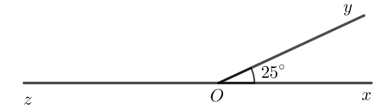
Do và là hai góc kề bù nên
Do đó = 180o - 25o = 155o.
Vậy = 155o.
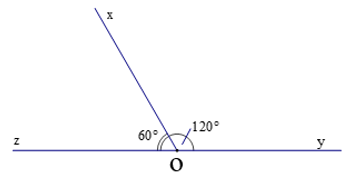
Bài 3 trang 72 Toán lớp 7 Tập 1: Cho hai góc kề nhau và với . Biết . Tính số đo các góc và .
Lời giải:
Do nên .80o = 16o.
Do (do hai góc và kề nhau) nên = 800 - 16o = 64o.
Vậy = 16o, = 64o.
Bài 4 trang 72 Toán lớp 7 Tập 1: Tìm số đo các góc còn lại trong mỗi hình sau.
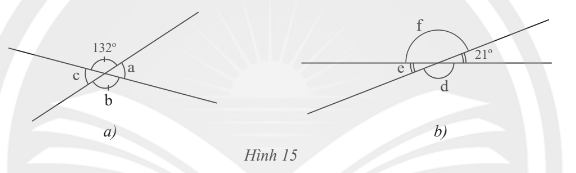
Lời giải:
+) Xét Hình 15a:
b là góc đối đỉnh với góc 132o nên b = 132o.
a là góc kề bù với góc 132o nên a + 132o = 180o.
Do đó a = 180o - 132o = 48o.
c = a do 2 góc này đối đỉnh.
Do đó c = 48o.
Vậy a = c = 48o, b = 132o.
+) Xét Hình 15b:
e là góc đối đỉnh với góc 21o nên e = 21o.
d là góc kề bù với góc 21o nên d + 21o = 180o.
Do đó d = 180o - 21o = 159o.
f = d do 2 góc này đối đỉnh.
Do đó f = 159o.
Vậy d = f = 159o, e = 21o.
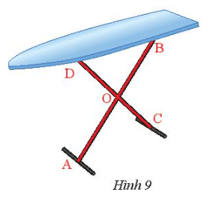
Lời giải:
Ta thấy a vuông góc với b, kí hiệu: .
a vuông góc với c, kí hiệu: .
Lý thuyết Toán 7 Bài 1: Các góc ở vị trí đặc biệt - Chân trời sáng tạo
1. Hai góc kề bù
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
Hai góc bù nhau là hai góc có tổng số đo bằng 1800.
Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.
Ví dụ:
a) Hai góc và có cạnh chung Oy và không có điểm trong chung. Vì thế, hai góc và là hai góc kề nhau.
b)
Ta có: .
Vì vậy, hai góc xOz và góc xOy là hai góc bù nhau.
Mặt khác: hai góc và có cạnh chung Ox và không có điểm trong chung nên hai góc và là hai góc kề nhau.
Vậy, hai góc và là hai góc kề bù.
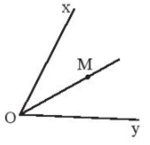
Chú ý : Nếu M là điểm trong của góc xOy thì .
2. Hai góc đối đỉnh
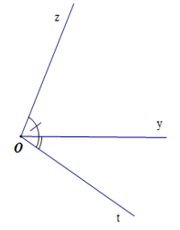
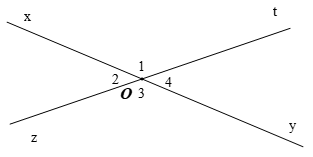
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Ví dụ :
Cạnh Oy của là tia đối của cạnh Ox của ;
Cạnh Ot của là tia đối của cạnh Oz của ;
Vì vậy, và là hai góc đối đỉnh.
Tương tự, góc và cũng là hai góc đối đỉnh.
Chú ý: Khi và là hai góc đối đỉnh, ta còn nói đối đỉnh với ; đối đỉnh với ; và đối đỉnh với nhau.
3. Tính chất của hai góc đối đỉnh
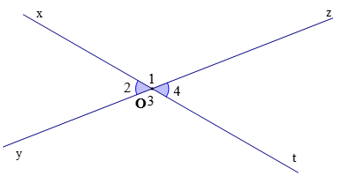
Hai góc đối đỉnh thì bằng nhau.
Ví dụ:
Hai góc và đối đỉnh với nhau.
Vì vậy, .
Tương tự, và là hai góc đối đỉnh, nên .
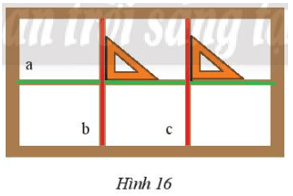
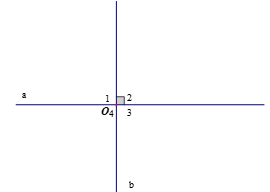
Chú ý: Hai đường thẳng vuông góc
Hai đường thẳng a và b cắt nhau tại O tạo thành bốn góc , , , .
Do tính chất của hai góc đối đỉnh hoặc kề bù, ta thấy trong bốn góc nêu trên, nếu có một góc vuông thì ba góc còn lại cũng là góc vuông.
Khi đó, ta nói hai đường thẳng a và b vuông góc với nhau và kí hiệu là a ⊥ b, hoặc b ⊥ a.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Hai đường thẳng song song
Bài 4: Định lí và chứng minh một định lí
Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 7 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Soạn văn lớp 7 (ngắn nhất) – Chân trời sáng tạo
- Văn mẫu lớp 7 – Chân trời sáng tạo
- Giải sgk Lịch sử 7 – Chân trời sáng tạo
- Lý thuyết Lịch Sử 7 – Chân trời sáng tạo
- Giải sbt Lịch sử 7 – Chân trời sáng tạo
- Giải sgk Địa lí 7 – Chân trời sáng tạo
- Lý thuyết Địa Lí 7 – Chân trời sáng tạo
- Giải sbt Địa lí 7 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 7 Friend plus – Chân trời sáng tạo
- Giải sbt Tiếng Anh 7 Friend plus– Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 7 Friends plus đầy đủ nhất
- Bài tập Tiếng Anh 7 Friends plus theo Unit có đáp án
- Giải sgk Khoa học tự nhiên 7 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 7 – Chân trời sáng tạo
- Giải sbt Khoa học tự nhiên 7 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 7 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 7 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 7 – Chân trời sáng tạo
- Giải sgk Công nghệ 7 – Chân trời sáng tạo
- Lý thuyết Công nghệ 7 – Chân trời sáng tạo
- Giải sbt Công nghệ 7 – Chân trời sáng tạo
- Giải sgk Tin học 7 – Chân trời sáng tạo
- Lý thuyết Tin học 7 – Chân trời sáng tạo
- Giải sbt Tin học 7 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 7 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 7 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 7 – Chân trời sáng tạo
- Giải sgk Âm nhạc 7 – Chân trời sáng tạo