Giải Toán 7 Bài 3 (Chân trời sáng tạo): Tam giác cân

Giải bài tập Toán 7 Bài 3: Tam giác cân 

A. Các câu hỏi trong bài

Giải Toán 7 trang 59 Tập 2

Khởi động trang 59 Toán 7 Tập 2:

Em hãy đo rồi so sánh độ dài hai cạnh AB và AC của tam giác ABC có trong hình di tích ga xe lửa Đà Lạt dưới đây.

Lời giải:

Dùng thước có vạch chia, ta đo được độ dài AB và AC của ∆ABC trong hình trên, ta được:

AB = 1 cm và AC = 1 cm.

Do đó AB = AC.

Vậy độ dài hai cạnh AB và AC của tam giác ABC có trong hình di tích ga xe lửa Đà Lạt bằng nhau.

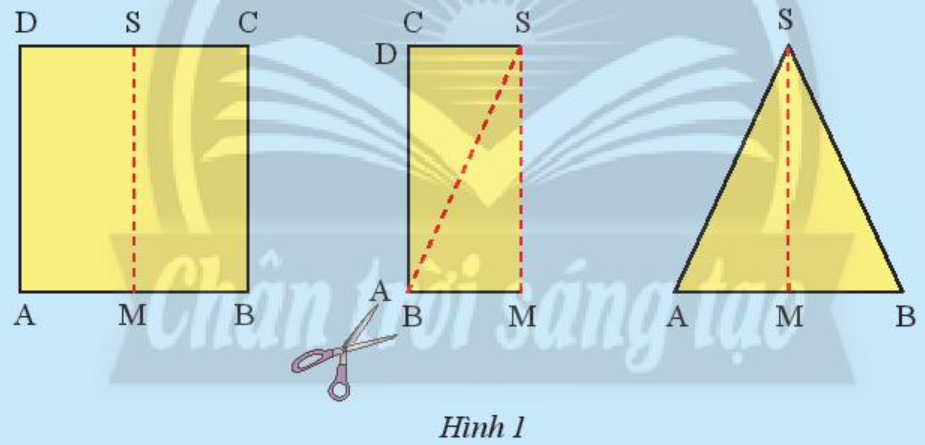
Khám phá 1 trang 59 Toán 7 Tập 2:

Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chéo AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.

Lời giải:

Thực hiện cắt và gấp theo hướng dẫn, ta thấy hai tam giác SAM và SBM đã được gấp chồng khít lên nhau nên ∆SAM = ∆SBM

Do đó SA = SB (hai cạnh tương ứng).

Vậy hai cạnh SA và SB của tam giác SAB bằng nhau.

Giải Toán 7 trang 60 Tập 2

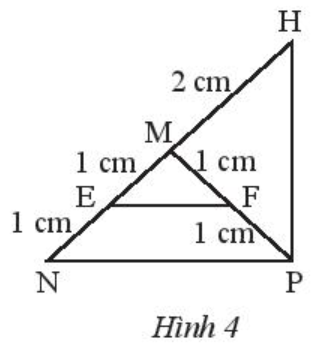
Thực hành 1 trang 60 Toán 7 Tập 2:

Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.

Lời giải:

Vì ∆MEF có ME = MF = 1 cm nên ∆MEF cân tại M.

Khi đó ∆MEF cân tại M có:

∙ ME và MF là hai cạnh bên;

∙ EF là cạnh đáy;

∙ $\widehat{EMF}$ là góc ở đỉnh;

∙ $\widehat{MEF}$ và $\widehat{MF\text{E}}$ là hai góc ở đáy.

Ta có: MN = ME + EN = 1 + 1 = 2 (cm);

           MP = MF + FP = 1 + 1 = 2 (cm).

Vì ∆MNP có MN = MP = 2 cm nên ∆MNP cân tại M.

Khi đó ∆MNP cân tại M có:

∙ MN và MP là hai cạnh bên;

∙ NP là cạnh đáy;

∙ $\widehat{NMP}$ là góc ở đỉnh;

∙ $\widehat{MNP}$ và $\widehat{MPN}$ là hai góc ở đáy.

Vì ∆MPH có MP = MH = 2 cm nên ∆MPH cân tại M.

Khi đó ∆MPH cân tại M có:

∙ MP và MH là hai cạnh bên;

∙ PH là cạnh đáy;

∙ $\widehat{PMH}$ là góc ở đỉnh;

∙ $\widehat{MPH}$ và $\widehat{MHP}$ là hai góc ở đáy.

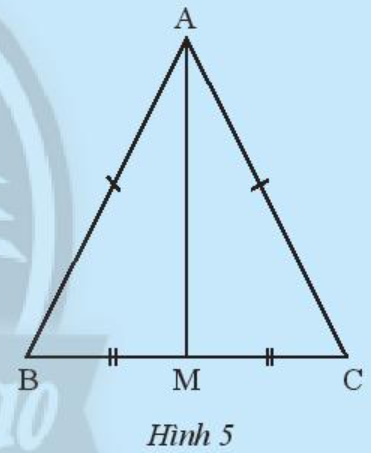
Khám phá 2 trang 60 Toán 7 Tập 2:

Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M.

Em hãy làm theo gợi ý sau để chứng minh $\widehat{ABC}=\widehat{ACB}$.

Xét ∆AMB và ∆AMC có:

AB = ? (?)

MB = MC (?)

AM là cạnh ?

Vậy ∆AMB = ∆AMC (c.c.c).

Suy ra $\widehat{ABC}=\widehat{ACB}$.

Lời giải:

Xét ∆AMB và ∆AMC có:

AB = AC (do ∆ABC cân tại A)

MB = MC (do M là trung điểm của BC)

AM là cạnh chung

Vậy ∆AMB = ∆AMC (c.c.c).

Suy ra $\widehat{ABC}=\widehat{ACB}$.

Giải Toán 7 trang 61 Tập 2

Thực hành 2 trang 61 Toán 7 Tập 2:

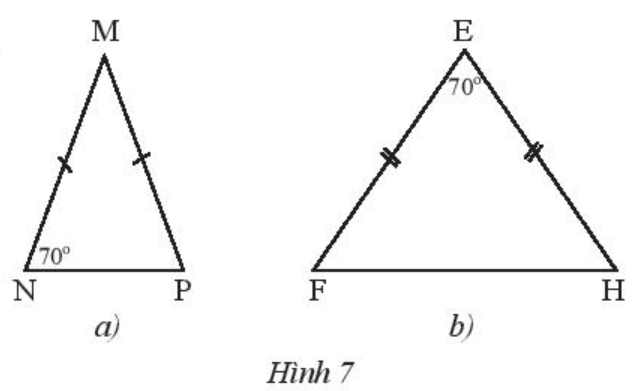
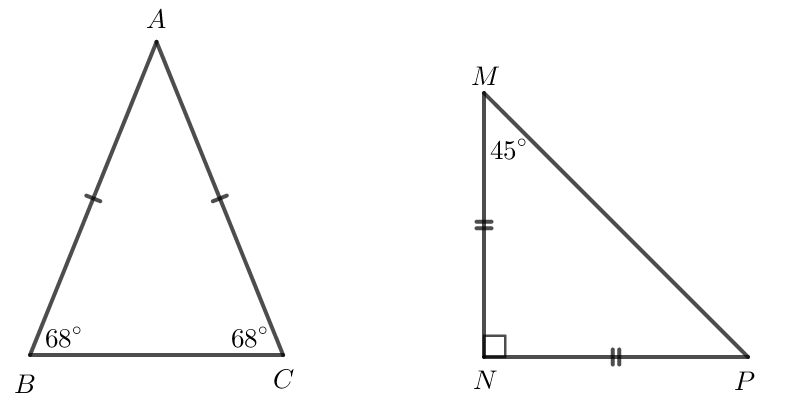
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.

Lời giải:

* Hình 7a):

Xét ∆MNP có MN = MP nên ∆MNP cân tại M.

Suy ra $\widehat{N}=\widehat{P}$ (hai góc ở đáy).

Do đó $\widehat{P}=70°$.

Xét $∆$MNP có: $\widehat{M}+\widehat{N}+\widehat{P}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{M}=180°-\widehat{N}-\widehat{P}$

Do đó $\widehat{M}=180°-70°-70°=40°$.

* Hình 7b):

Xét ∆EFH có EF = EH nên ∆EFH cân tại E.

Do đó $\widehat{F}=\widehat{H}$ (hai góc ở đáy).

Xét $∆$EFH có: $\widehat{\text{E}}+\widehat{F}+\widehat{H}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{F}+\widehat{H}=180°-\widehat{E}$ 

Hay $2\widehat{F}=180°-70°=110°$.

Do đó $\widehat{F}=\widehat{H}=\frac{110°}{2}=55°$.

Vậy $\widehat{M}=40°$; $\widehat{P}=70°$; $\widehat{F}=\widehat{H}=55°$.

Vận dụng 1 trang 61 Toán 7 Tập 2:

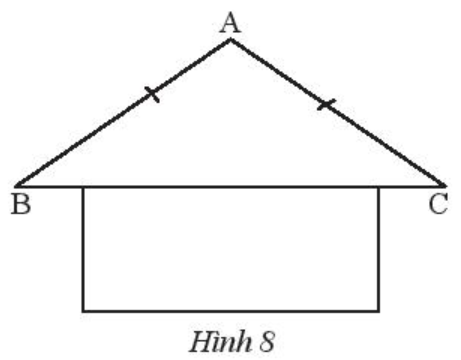
Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết $\widehat{A}=110°$.

Lời giải:

Xét ∆ABC có AB = AC nên ∆ABC cân tại A.

Do đó $\widehat{B}=\widehat{C}$ (hai góc ở đáy).

Xét $∆$ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}$

Do đó $\widehat{B}=180°-110°=70°$.

Vậy $\widehat{B}=\widehat{C}=35°$.

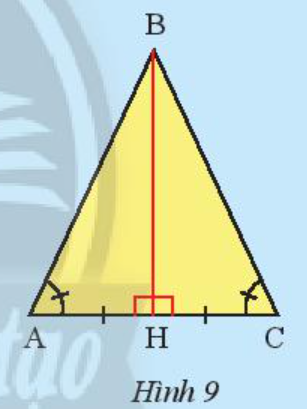
Khám phá 3 trang 61 Toán 7 Tập 2:

Cho tam giác ABC có $\widehat{A}=\widehat{C}$. Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.

Xét ∆AHB và ∆CHB cùng vuông tại H, ta có:

BH là cạnh góc vuông ?;

$\widehat{HAB}=\widehat{HCB}$ suy ra $\widehat{ABH}=\widehat{CBH}$ (?).

Vậy ∆AHB = ∆CHB. Suy ra BA = BC.

Lời giải:

Xét ∆AHB và ∆CHB cùng vuông tại H, ta có:

BH là cạnh góc vuông chung;

$\widehat{HAB}=\widehat{HCB}$ suy ra $\widehat{ABH}=\widehat{CBH}$ (do $\widehat{ABH}=90°-\widehat{HAB}$ và $\widehat{CBH}=90°-\widehat{HCB}$).

Vậy ∆AHB = ∆CHB. Suy ra BA = BC.

Giải Toán 7 trang 62 Tập 2

Thực hành 3 trang 62 Toán 7 Tập 2:

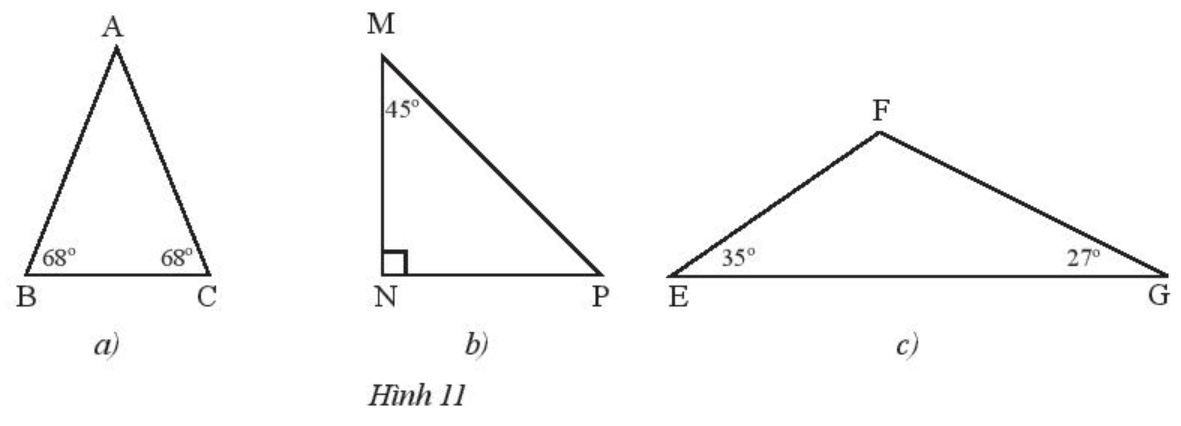
Tìm các tam giác cân trong Hình 11 và đánh dấu các cạnh bằng nhau.

Lời giải:

• Xét ∆ABC có $\widehat{B}=\widehat{C}=68°$ nên ∆ABC cân tại A.

Suy ra AB = AC (hai cạnh bên).

• Xét ∆MNP vuông tại N nên $\widehat{M}+\widehat{P}=90°$.

Suy ra $\widehat{P}=90°-\widehat{M}=90°-45°=45°$.

∆MNP có $\widehat{NMP}=\widehat{NPM}=45°$ nên ∆MNP cân tại N.

Suy ra NM = NP (hai cạnh bên).

• Xét ∆EFG có: $\widehat{E}+\widehat{F}+\widehat{G}=180°$ (định lí tổng số đo ba góc của một tam giác)

Hay $35°+\widehat{F}+27°=180°$

Suy ra $\widehat{F}=180°-35°-27°=118°$.

Do đó $\widehat{E}=35°$; $\widehat{G}=27°$; $\widehat{F}=118°$.

Vì ∆EFG không có hai góc nào bằng nhau nên ∆EFG không phải tam giác cân.

Do đó các cặp cạnh bằng nhau trong Hình 7 là: AB = AC; MN = NP và được đánh dấu như hình vẽ sau:

Vận dụng 2 trang 62 Toán 7 Tập 2:

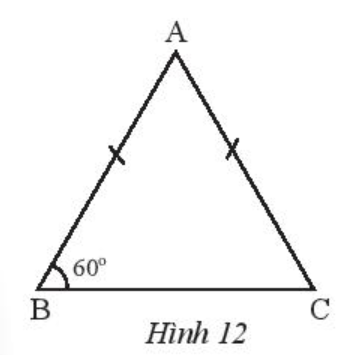
Cho tam giác ABC cân tại A có góc B bằng 60^o. Chứng minh rằng tam giác ABC đều.

Lời giải:

Ta có ∆ABC cân tại A nên AB = AC và $\widehat{B}=\widehat{C}=60°$.

Xét $∆$ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{A}=180°-\widehat{B}-\widehat{C}$

Do đó $\widehat{A}=180°-60°-60°=60°$.

Ta có ∆ABC có $\widehat{B}=\widehat{A}$ nên tam giác ABC cân tại C.

Suy ra CA = CB.

Mà AB = AC nên AB = AC = BC.

Vậy tam giác ABC là tam giác đều.

B. Bài tập

Bài 1 trang 62 Toán 7 Tập 2:

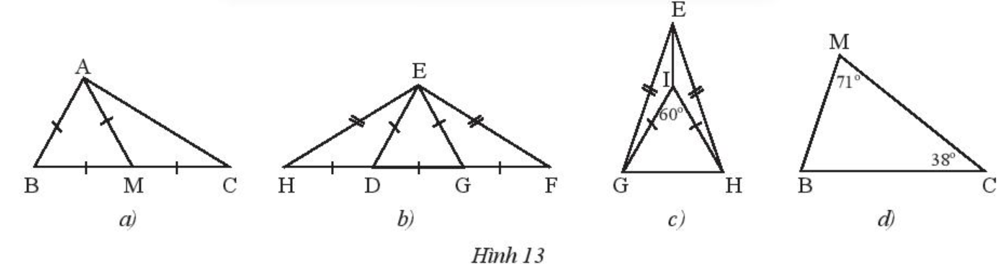
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.

Lời giải:

* Hình 13a):

Vì ∆AMC có AM = MC nên ∆AMC cân tại M.

Vì ∆ABM có AB = AM = BM nên ∆ABM đều.

* Hình 13b):

Vì ∆DEH có DE = DH nên ∆DEH cân tại D.

Vì ∆GEF có GE = GF nên ∆GEF cân tại G.

Vì ∆EHF có EH = EF nên ∆EHF cân tại E.

Do đó các tam giác cân: ∆DEH, ∆GEF, ∆EHF.

Vì ∆EDG có DE = EG = DG nên ∆EDG đều.

* Hình 13c):

Vì ∆EGH có EG = EH nên ∆EGH cân tại E.

Vì ∆IGH có IG = IH nên ∆IGH cân tại I.

∆IGH cân có $\widehat{GIH}=60°$ nên ∆IGH là tam giác đều.

* Hình 13d):

Xét ∆MBC có $\widehat{M}+\widehat{B}+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{B}=180°-\widehat{M}-\widehat{C}$

Do đó $\widehat{B}=180°-71°-38°=71°$.

Vì ∆MBC có $\widehat{M}=\widehat{B}$ nên ∆MBC cân tại C.

Bài 2 trang 62 Toán 7 Tập 2:

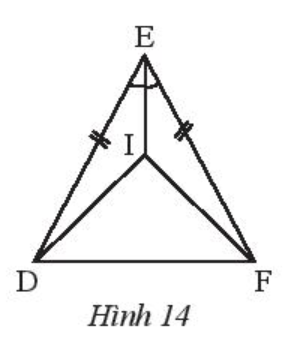
Cho Hình 14, biết ED = EF và EI là tia phân giác của $\widehat{DEF}$.

Chứng minh rằng:

a) ∆EID = ∆EIF.

b) Tam giác DIF cân.

Lời giải:

a) Xét ∆EID và ∆EIF có:

ED = EF (giả thiết);

$\widehat{DEI}=\widehat{F\text{E}I}$ (do EI là tia phân giác của $\widehat{DEF}$);

EI là cạnh chung.

Do đó ∆EID = ∆EIF (c.g.c).

b) Từ câu a: ∆EID = ∆EIF.

Suy ra ID = IF (hai cạnh tương ứng).

Tam giác DIF có ID = IF nên tam giác DIF cân tại I.

Giải Toán 7 trang 63 Tập 2

Bài 3 trang 63 Toán 7 Tập 2:

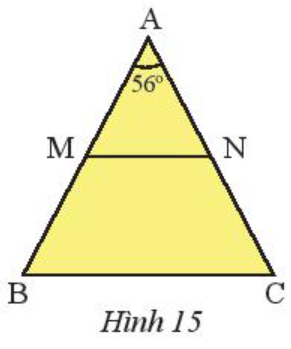
Cho tam giác ABC cân tại A có $\widehat{A}=56°$ (Hình 15).

a) Tính $\widehat{B},\widehat{C}$.

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.

c) Chứng minh rằng MN // BC.

Lời giải:

a) Theo đề bài: ∆ABC cân tại A nên $\widehat{B}=\widehat{C}$.

Xét ∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}$.

Do đó $2\widehat{B}=180°-56°=124°$ (vì $\widehat{B}=\widehat{C}$) nên $\widehat{B}=\frac{124°}{2}=62°$

Vậy $\widehat{B}=\widehat{C}=62°$.

b) Vì M là trung điểm của AB nên:

AM = $\frac{1}{2}$AB hay AB = 2AM.

Vì N là trung điểm của AC nên:

AN = $\frac{1}{2}$AC hay AC = 2AN.

Mà ∆ABC cân tại A nên AB = AC hay 2AM = 2AN.

Do đó AM = AN.

Tam giác AMN có AM = AN nên tam giác AMN cân tại A.

Vậy tam giác AMN cân tại A.

c) Vì ∆AMN cân tại A nên $\widehat{AMN}=\widehat{ANM}$.

Xét ∆AMN có $\widehat{A}+\widehat{AMN}+\widehat{ANM}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{AMN}+\widehat{ANM}=180°-\widehat{A}$.

Hay $2\widehat{AMN}=180°-56°=124°$.

Do đó $\widehat{AMN}=\widehat{ANM}=62°$.

Khi đó $\widehat{ABC}=\widehat{AMN}=62°$.

Mà hai góc này ở vị trí đồng vị nên MN // BC.

Vậy MN // BC.

Bài 4 trang 63 Toán 7 Tập 2:

Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

a) Chứng minh rằng $\widehat{ABF}=\widehat{ACE}$.

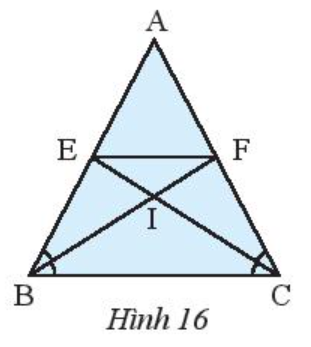
b) Chứng minh rằng tam giác AEF cân.

c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân.

Lời giải:

a) Theo đề bài, tam giác ABC cân tại A nên:

AB = AC và $\widehat{ABC}=\widehat{ACB}$.

Vì BF là tia phân giác của $\widehat{ABC}$ nên: $\widehat{ABF}=\widehat{FBC}=\frac{1}{2}\widehat{ABC}$ 

Vì CE là tia phân giác của $\widehat{ACB}$ nên: $\widehat{AC\text{E}}=\widehat{ECB}=\frac{1}{2}\widehat{ACB}$ 

Mà $\widehat{ABC}=\widehat{ACB}$ nên $\widehat{ABF}=\widehat{FBC}=\widehat{AC\text{E}}=\widehat{ECB}$

Vậy $\widehat{ABF}=\widehat{AC\text{E}}$.

b) Xét ∆ABF và ∆ACE có:

$\widehat{ABF}=\widehat{AC\text{E}}$ (chứng minh câu a);

AB = AC (chứng minh trên);

$\widehat{A}$ là góc chung.

Do đó ∆ABF = ∆ACE (g.c.g).

Suy ra AF = AE (hai cạnh tương ứng).

Tam giác AEF có AF = AE nên tam giác AEF cân tại A.

c) Ta có $\widehat{FBC}=\widehat{ECB}$ (chứng minh câu a) nên $\widehat{IBC}=\widehat{ICB}$.

Tam giác IBC có $\widehat{IBC}=\widehat{ICB}$ nên tam giác IBC cân tại I.

Do đó IB = IC.

Xét ∆EIB và ∆FIC có:

$\widehat{EIB}=\widehat{FIC}$ (hai góc đối đỉnh);

IB = IC (chứng minh trên);

$\widehat{EBI}=\widehat{FCI}$ (do $\widehat{ABF}=\widehat{AC\text{E}}$).

Do đó ∆EIB = ∆FIC (g.c.g).

Suy ra IE = IF (hai cạnh tương ứng).

Tam giác IEF có IE = IF nên tam giác IEF cân tại I.

Bài 5 trang 63 Toán 7 Tập 2:

Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và $\widehat{B}=35°$. Tìm số đo các góc còn lại và chu vi của tam giác ABC.

Lời giải:

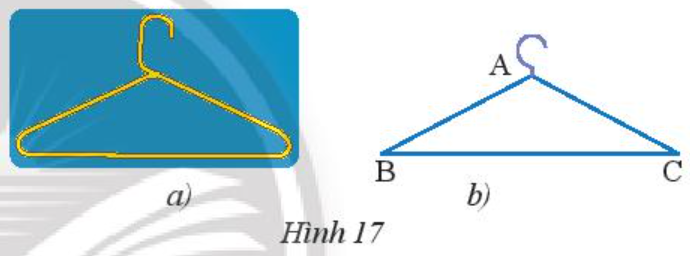
Phần thân của một móc treo quần áo có dạng hình tam giác cân nên:

Trong Hình 17b: tam giác ABC cân tại A.

Suy ra AB = AC và $\widehat{B}=\widehat{C}$.

Do đó AB = AC = 20 cm; $\widehat{B}=\widehat{C}=35°$.

Xét ∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{A}=180°-\widehat{B}-\widehat{C}$

Do đó $\widehat{A}=180°-35°-35°=110°$.

Chu vi tam giác ABC là:

AB + BC + AC = 20 + 28 + 20 = 68 (cm).

Vậy số đo các góc còn lại là: $\widehat{A}=110°$, $\widehat{C}=35°$ và chu vi tam giác ABC là 68 cm.

Bài 6 trang 63 Toán 7 Tập 2:

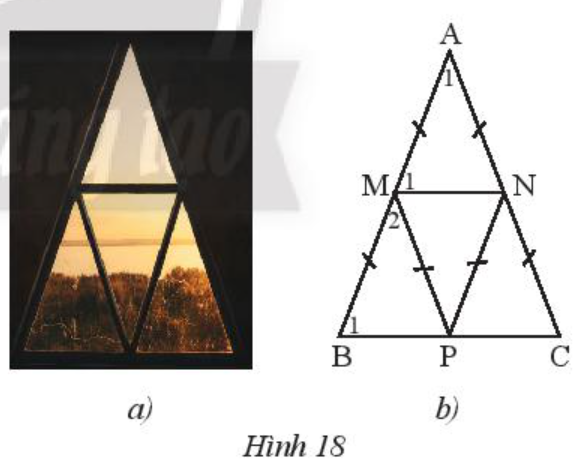
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

a) Cho biết ${\widehat{A}}_1=42°$. Tính số đo của ${\widehat{M}}_1,{\widehat{B}}_1,{\widehat{M}}_2$.

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Lời giải:

a) ∆AMN có AM = AN nên ∆AMN cân tại A.

Suy ra ${\widehat{M}}_1=\widehat{ANM}$.

Xét ∆AMN có: ${\widehat{A}}_1+{\widehat{M}}_1+\widehat{ANM}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra ${\widehat{M}}_1+\widehat{ANM}=180°-{\widehat{A}}_1$.

Hay $2{\widehat{M}}_1=180°-{\widehat{A}}_1=180°-42°=138°$.

Do đó ${\widehat{M}}_1=69°$.

Ta có: AB = AM + MB; AC = AN + NC.

Mà AM = AN, MB = NC nên AB = AC.

Do đó ∆ABC cân tại A.

Suy ra ${\widehat{B}}_1=\widehat{C}$.

Xét ∆ABC có: ${\widehat{A}}_1+{\widehat{B}}_1+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra ${\widehat{B}}_1+\widehat{C}=180°-{\widehat{A}}_1$.

Hay $2{\widehat{B}}_1=180°-{\widehat{A}}_1=180°-42°=138°$.

Do đó ${\widehat{B}}_1=69°$.

∆MBP có MB = MP nên ∆MBP cân tại M.

Suy ra $\widehat{MBP}=\widehat{MPB}$.

Xét ∆MBP có: ${\widehat{M}}_2+{\widehat{B}}_1+\widehat{MPB}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra ${\widehat{M}}_2=180°-{\widehat{B}}_1-\widehat{MPB}$.

Hay ${\widehat{M}}_2=180°-2{\widehat{B}}_1=180°-2.69°=42°$.

Vậy ${\widehat{M}}_1=69°$; ${\widehat{B}}_1=69°$; ${\widehat{M}}_2=42°$.

b) Ta có: ${\widehat{M}}_1={\widehat{B}}_1=69°$.

Mà ${\widehat{M}}_1$ và ${\widehat{B}}_1$ ở vị trí đồng vị nên MN // BC.

Lại có: ${\widehat{M}}_2={\widehat{A}}_1=42°$.

Mà ${\widehat{M}}_2$ và ${\widehat{A}}_1$ ở vị trí đồng vị nên MP // AC.

c) • Xét ∆AMN và ∆MBP có:

AM = MB (giả thiết).

${\widehat{A}}_1={\widehat{M}}_2$ (chứng minh trên).

AN = MP (giả thiết).

Do đó ∆AMN = ∆MBP (c.g.c).

Suy ra MN = BP (hai cạnh tương ứng).

• Xét ∆MBP và ∆PMN có:

MP = PN (giả thiết).

MB = PM (giả thiết).

BP = MN (chứng minh trên).

Do đó ∆MBP = ∆PMN (c.c.c).

• Do MP // AC nên $\widehat{MPN}=\widehat{PNC}$ (hai góc so le trong).

Xét ∆PMN và ∆NPC có:

PM = NP (giả thiết).

$\widehat{MPN}=\widehat{PNC}$ (chứng minh trên).

PN = NC (giả thiết).

Do đó ∆PMN = ∆NPC (c.g.c).

Vậy bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 2: Tam giác bằng nhau

Bài 3: Tam giác cân

Bài 4: Đường vuông góc và đường xiên

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác