Giải Toán 7 Bài 2 (Chân trời sáng tạo): Làm quen với xác suất của biến cố ngẫu nhiên

Giải bài tập Toán 7 Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên 

A. Các câu hỏi trong bài

Giải Toán 7 trang 90 Tập 2

Khởi động trang 90 Toán 7 Tập 2:

An và Bình chơi trò tung một đồng xu cân đối. Nếu An tung được mặt sấp thì An thắng, còn nếu tung được mặt ngửa thì Bình thắng.

Theo em bạn nào có khả năng giành phần thắng cao hơn?

Lời giải:

Theo em, hai bạn có khả năng giành phần thắng như nhau, vì khả năng tung được mặt sấp và mặt ngửa là như nhau.

Khám phá 1 trang 90 Toán 7 Tập 2:

Một hộp có 5 chiếc thẻ cùng loại được đánh số lần lượt từ 1 đến 5. Lấy ngẫu nhiên một chiếc thẻ từ hộp. Hãy so sánh khả năng của các biến cố sau:

A: “Thẻ lấy ra được ghi số lẻ”;

B: “Thẻ lấy ra được ghi số chẵn”;

C: “Thẻ lấy ra được ghi số 2”.

Lời giải:

Từ 1 đến 5 có ba số lẻ là: 1; 3; 5.

Từ 1 đến 5 có hai số chẵn là: 2; 4.

Do trong hộp có 3 thẻ được ghi số lẻ và 2 thẻ được ghi số chẵn nên khả năng thẻ lấy ra được ghi số lẻ cao hơn khả năng thẻ lấy ra được ghi số chẵn. Hay biến cố A có khả năng xảy ra cao hơn biến cố B.

Mặt khác:

+ Nếu thẻ lấy ra được ghi số 2 thì biến cố B và C đều xảy ra;

+ Nếu thẻ lấy ra được ghi số 4 thì biến cố B xảy ra, biến cố C không xảy ra.

Do đó biến cố B có khả năng xảy ra cao hơn biến cố C.

Vậy biến cố A có khả năng xảy ra cao hơn biến cố B, biến cố B có khả năng xảy ra cao hơn biến cố C.

Giải Toán 7 trang 91 Tập 2

Thực hành 1 trang 91 Toán 7 Tập 2:

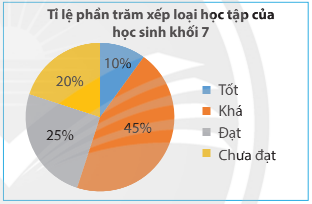
Kết quả xếp loại học tập cuối học kì 1 của học sinh khối 7 được cho ở biểu đồ bên.

Gặp ngẫu nhiên một học sinh khối 7.

a) Xác suất học sinh đó được xếp loại học lực nào là cao nhất?

b) Xác suất học sinh đó được xếp loại học lực nào là thấp nhất?

Lời giải:

Dựa vào biểu đồ, tỉ lệ phần trăm số học sinh xếp loại Tốt, Khá, Đạt, Chưa đạt lần lượt là 10%; 45%; 25% và 20%.

Ta có: 10% < 20% < 25% < 45%.

Khi đó:

a) Xác suất học sinh đó được xếp loại học lực Khá là cao nhất (45%).

b) Xác suất học sinh đó được xếp loại học lực Tốt là thấp nhất (10%).

Khám phá 2 trang 91 Toán 7 Tập 2:

Gieo một con xúc xắc cân đối. Hãy so sánh xác suất của các biến cố sau:

A: “Mặt xuất hiện có 2 chấm”;

B: “Mặt xuất hiện có 3 chấm”.

Lời giải:

Gieo một con xúc xắc cân đối, số chấm xuất hiện trên mặt con xúc xắc có thể xảy ra các khả năng: 1 chấm; 2 chấm; 3 chấm; 4 chấm; 5 chấm; 6 chấm.

Do con xúc xắc cân đối nên biến cố A, biến cố B đều chỉ có 1 khả năng xảy ra.

Vậy xác suất của biến cố A và biến cố B bằng nhau.

Giải Toán 7 trang 92 Tập 2

Thực hành 2 trang 92 Toán 7 Tập 2:

Gieo một con xúc xắc 6 mặt cân đối. Tính xác suất của các biến cố sau:

a) A: “Gieo được mặt có số chấm lớn hơn 5”;

b) B: “Gieo được mặt có số chấm nhỏ hơn 7”.

Lời giải:

a) Số chấm xuất hiện trên mặt của con xúc xắc có thể là: 1 chấm; 2 chấm; 3 chấm; 4 chấm; 5 chấm; 6 chấm.

Gieo được mặt có số chấm lớn hơn 5 tức là gieo được mặt có 6 chấm.

Con xúc xắc có 6 mặt cân đối và trong 6 mặt đó chỉ có 1 mặt có 6 chấm.

Vì 6 kết quả có khả năng xảy ra bằng nhau nên P(A) = $\frac{1}{6}$.

Vậy xác suất của biến cố A bằng $\frac{1}{6}$.

b) Số chấm trên các mặt của con xúc xắc đều nhỏ hơn 7.

Do đó biến cố B là biến cố chắc chắn nên P(B) = 1.

Vậy xác suất của biến cố B bằng 1.

Khám phá 3 trang 92 Toán 7 Tập 2:

Một bình có 4 quả bóng có kích thước và khối lượng giống nhau, trong đó có 1 quả màu xanh, 1 quả màu vàng, 1 quả màu đỏ và 1 quả màu trắng. Lấy ra ngẫu nhiên 1 quả bóng từ bình. Hãy liệt kê các kết quả có thể xảy ra.

Lời giải:

Lấy ra ngẫu nhiên 1 quả bóng từ bình có 4 quả bóng (kích thước và khối lượng giống nhau).

Khi đó, quả bóng lấy ra có thể có 1 trong 4 màu: xanh hoặc vàng hoặc đỏ hoặc trắng.

Vậy các kết quả có thể xảy ra là: xanh; vàng; đỏ; trắng.

Thực hành 3 trang 92 Toán 7 Tập 2:

Tính xác suất giành phần thắng của bạn An và của bạn Bình trong trò chơi ở Khởi động (trang 90).

Lời giải:

Vì đồng xu hai mặt cân đối nên có hai kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là mặt sấp; mặt ngửa và hai kết quả trên đều có cùng khả năng xảy ra.

Do đó, xác suất giành phần thắng của bạn An bằng xác suất giành phần thắng của bạn Bình và đều bằng $\frac{1}{2}$.

Giải Toán 7 trang 93 Tập 2

Thực hành 4 trang 93 Toán 7 Tập 2:

Một hộp có 10 lá thăm có kích thước giống nhau và được đánh số từ 1 đến 10. Lấy ngẫu nhiên 1 lá thăm từ hộp.

a) Hãy nêu các điểm cần lưu ý khi tính xác suất liên quan đến hoạt động trên.

b) Gọi A là biến cố “Lấy được lá thăm ghi số 9”. Hãy tính xác suất của biến cố A.

c) Gọi B là biến cố “Lấy được lá thăm ghi số nhỏ hơn 11”. Hãy tính xác suất của biến cố B.

Lời giải:

a) Các điểm cần lưu ý khi tính xác suất của hoạt động trên là:

- Có 10 kết quả xảy ra.

- Do 10 lá thăm có kích thước giống nhau và được đánh số khác nhau từ 1 đến 10 nên mỗi kết quả có cùng khả năng xảy ra.

b) Trong một hộp có 10 lá thăm có kích thước giống nhau và được đánh số từ 1 đến 10 nên có 1 lá thăm ghi số 9.

Do đó xác suất lấy được lá thăm ghi số 9 là: P(A) = $\frac{1}{10}$.

Vậy xác suất của biến cố A bằng $\frac{1}{10}$.

c) Trong một hộp có 10 lá thăm có kích thước giống nhau và được đánh số từ 1 đến 10 thì 10 lá thăm đều ghi số nhỏ hơn 11.

Do đó biến cố B là biến cố chắc chắn nên P(B) = 1.

Vậy xác suất của biến cố B bằng 1.

Vận dụng trang 93 Toán 7 Tập 2:

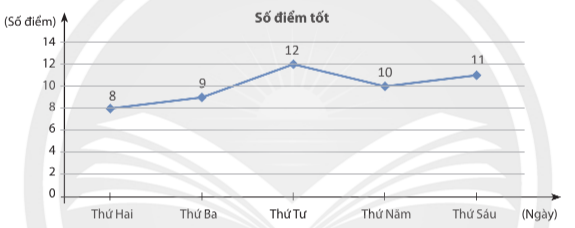
Số điểm tốt các bạn học sinh lớp 7B đạt được trong một tuần được cho ở biểu đồ đoạn thẳng sau.

Chọn ngẫu nhiên một ngày trong tuần. Biết rằng khả năng cả 5 ngày được chọn đều như nhau. Tính xác suất của biến cố:

a) “Vào ngày được chọn các học sinh lớp 7B đạt 10 điểm tốt”.

b) “Vào ngày được chọn các học sinh lớp 7B đạt ít nhất 8 điểm tốt”.

Lời giải:

Chọn ngẫu nhiên một ngày trong tuần và khả năng cả 5 ngày được chọn đều như nhau nên có 5 kết quả có thể xảy ra đối với ngày được chọn và 5 kết quả này có cùng khả năng xảy ra.

a) Trong 5 ngày chỉ có ngày thứ Năm các học sinh lớp 7B đạt 10 điểm tốt.

Do đó xác suất của biến cố “Vào ngày được chọn các học sinh lớp 7B đạt 10 điểm tốt” là $\frac{1}{5}$.

b) Trong cả 5 ngày thì số điểm tốt của các học sinh lớp 7B đều lớn hơn hoặc bằng 8.

Hay các học sinh lớp 7B đạt ít nhất 8 điểm tốt.

Do đó biến cố “Vào ngày được chọn các học sinh lớp 7B đạt ít nhất 8 điểm tốt” là biến cố chắc chắn, khi đó xác suất của biến cố này bằng 1.

B. Bài tập

Bài 1 trang 93 Toán 7 Tập 2:

Một tấm bìa hình tròn được chia thành 6 phần bằng nhau như Hình 1. Bạn Minh đặt tấm bìa nằm thẳng trên bàn, quay mũi tên ở tâm và quan sát xem khi dừng lại thì mũi tên chỉ vào ô nào.

Hãy so sánh xác suất xảy ra của các biến cố sau:

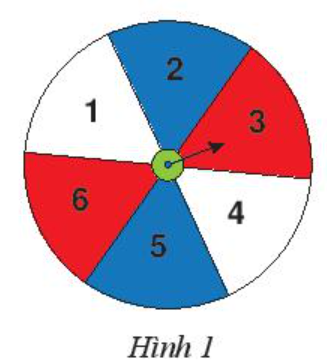
A: “Mũi tên chỉ vào ô có màu đỏ”;

B: “Mũi tên chỉ vào ô ghi số 3”;

C: “Mũi tên chỉ vào ô ghi số lớn hơn 2”.

Lời giải:

Do tấm bìa hình tròn được chia thành 6 phần bằng nhau nên khi quay mũi tên thì có 6 kết quả có thể xảy ra đối với ô được mũi tên chỉ vào và 6 kết quả này có cùng khả năng xảy ra.

• Xét biến cố A: “Mũi tên chỉ vào ô có màu đỏ”.

Trong 6 ô có 2 ô màu đỏ.

Do đó xác suất của biến cố này là: $P\left(A\right)=\frac{2}{6}=\frac{1}{3}$.

• Xét biến cố B: “Mũi tên chỉ vào ô ghi số 3”.

Trong 6 ô, chỉ có 1 ô ghi số 3.

Do đó xác suất của biến cố này là: $P\left(B\right)=\frac{1}{6}$.

• Xét biến cố C: “Mũi tên chỉ vào ô ghi số lớn hơn 2”.

Trong 6 ô, có 4 ô được ghi số lớn hơn 2 (là các ô ghi số 3; 4; 5; 6).

Do đó xác suất của biến cố này là: $P\left(C\right)=\frac{4}{6}=\frac{2}{3}$.

Ta có $\frac{1}{6}<\frac{1}{3}<\frac{2}{3}$ nên P(B) < P (A) < P(C).

Vậy xác suất xảy ra biến cố A lớn hơn biến cố B và nhỏ hơn biến cố C.

Bài 2 trang 93 Toán 7 Tập 2:

Một hộp có chứa 100 chiếc thẻ cùng loại, trong đó chỉ có 1 thẻ được đánh dấu là Thẻ may mắn. Bình lấy ra ngẫu nhiên 1 thẻ. Tính xác suất của biến cố “Thẻ lấy ra là Thẻ may mắn”.

Lời giải:

Bình lấy ra ngẫu nhiên 1 thẻ trong 100 chiếc thẻ cùng loại nên có 100 kết quả có thể xảy ra đối với thẻ được lấy và 100 kết quả này có cùng khả năng xảy ra.

Do chỉ có 1 thẻ được đánh dấu là Thẻ may mắn nên xác suất của biến cố “Thẻ lấy ra là Thẻ may mắn” là $\frac{1}{100}$.

Giải Toán 7 trang 94 Tập 2

Bài 3 trang 94 Toán 7 Tập 2:

Gieo một con xúc xắc cân đối. Tính xác suất của các biến cố sau:

a) A: “Gieo được mặt có số chấm bằng 4”.

b) B: “Gieo được mặt có số chấm chia hết cho 5”.

c) C: “Gieo được mặt có số chấm là số tròn chục”.

Lời giải:

Một con xúc xắc có số chấm ở các mặt là: 1 chấm; 2 chấm; 3 chấm; 4 chấm; 5 chấm; 6 chấm.

Gieo một con xúc xắc cân đối sẽ có 6 kết quả có thể xảy ra đối với số chấm xuất hiện và 6 kết quả này có cùng khả năng xảy ra.

a) Xét biến cố A: “Gieo được mặt có số chấm bằng 4”.

Trong 6 mặt chỉ có 1 mặt có số chấm bằng 4.

Do đó xác suất của biến cố A là: $P\left(A\right)=\frac{1}{6}.$

Vậy xác suất của biến cố A bằng $\frac{1}{6}$.

b) Xét biến cố B: “Gieo được mặt có số chấm chia hết cho 5”.

Trong 6 mặt chỉ có 1 mặt có số chấm chia hết cho 5 là mặt 5 chấm.

Do đó xác suất của biến cố B là: $P\left(B\right)=\frac{1}{6}.$

Vậy xác suất của biến cố B bằng $\frac{1}{6}$.

c) Xét biến cố C: “Gieo được mặt có số chấm là số tròn chục”.

Không có mặt nào có số chấm là số tròn chục.

Do đó biến cố C là biến cố không thể nên P(C) = 0.

Vậy xác suất của biến cố C bằng 0.

Bài 4 trang 94 Toán 7 Tập 2:

Đội múa có 1 bạn nam và 5 bạn nữ. Chọn ngẫu nhiên 1 bạn để phỏng vấn. Biết mỗi bạn đều có cùng khả năng được chọn. Hãy tính xác suất của biến cố bạn được chọn là nam.

Lời giải:

Chọn ngẫu nhiên 1 bạn trong 6 bạn để phỏng vấn nên có 6 kết quả có thể xảy ra; mỗi bạn đều có cùng khả năng được chọn nên 6 kết quả này có cùng khả năng xảy ra.

Trong 6 bạn ở đội múa chỉ có 1 bạn nam.

Do đó xác suất của biến cố bạn được chọn là nam bằng $\frac{1}{6}$.

Bài 5 trang 94 Toán 7 Tập 2:

Lượng điện tiêu thụ mỗi ngày trong 5 ngày đầu tháng 9/2021 của một hộ gia đình được cho ở biểu đồ sau. Chọn ngẫu nhiên 1 ngày trong 5 ngày đó. Hãy tính xác suất của biến cố “Hộ gia đình sử dụng 10 kWh điện trong ngày được chọn”.

Lời giải:

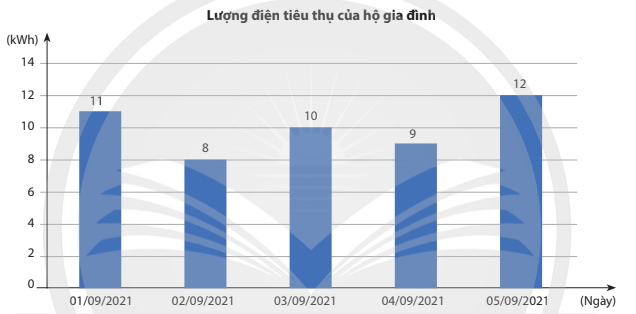
Chọn ngẫu nhiên 1 ngày trong 5 ngày nên có 5 kết quả có thể xảy ra và mỗi ngày có khả năng được chọn như nhau nên 5 kết quả này có cùng khả năng xảy ra.

Trong 5 ngày đầu tháng 9/2021 chỉ có ngày 03/09/2021 lượng điện tiêu thụ của hộ gia đình là 10 kWh.

Do đó xác suất để hộ gia đình sử dụng 10 kWh điện trong ngày được chọn là $\frac{1}{5}$.

Vậy xác suất của biến cố “Hộ gia đình sử dụng 10 kWh điện trong ngày được chọn” bằng $\frac{1}{5}$.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 1: Làm quen với biến cố ngẫu nhiên

Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên

Bài 3: Hoạt động thực hành và trải nghiệm. Nhảy theo xúc xắc

Bài tập cuối chương 9

Bài 1: Tập hợp các số hữu tỉ