Toán 7 Bài 1 (Chân trời sáng tạo): Hình hộp chữ nhật - Hình lập phương
Với giải bài tập Toán lớp 7 Bài 1: Hình hộp chữ nhật - Hình lập phương sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 1.
Giải bài tập Toán 7 Bài 1: Hình hộp chữ nhật - Hình lập phương
Video giải bài tập Toán 7 Bài 1: Hình hộp chữ nhật - Hình lập phương
Hoạt động khởi động
Lời giải:
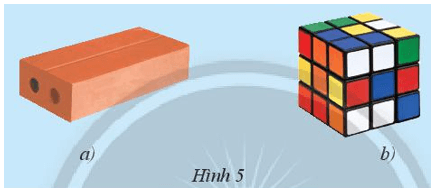
Hộp quà, các thùng giấy, thùng chứa hàng có dạng hình hộp chữ nhật.
Khối vuông rubik và con xúc xắc có dạng hình lập phương.
1. Hình hộp chữ nhật
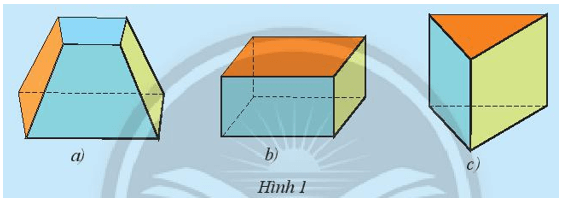
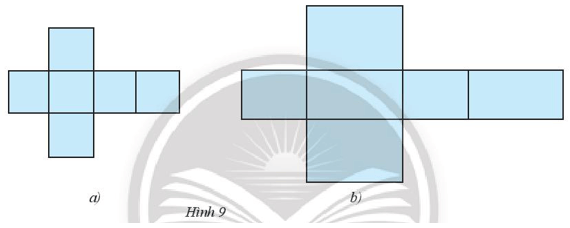
Khám phá 1 trang 47 Toán lớp 7 Tập 1: Hình nào dưới đây có sáu mặt đều là hình chữ nhật?
Lời giải:
Hình b có sáu mặt đều là hình chữ nhật.
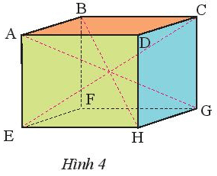
- Nêu các đường chéo được vẽ trong hình.
- Nêu các đường chéo chưa được vẽ trong hình.
Lời giải:
- Các góc ở đỉnh F: ^BFG;^BFE;^EFG.ˆBFG;ˆBFE;ˆEFG.
- Các đường chéo được vẽ trong hình: AG, BH, CE.
- Đường chéo chưa được vẽ là đường DF.
Lời giải:
Vì AB = DC nên AB = 5 cm (do ABCD là hình chữ nhật)
Vì FG = BC, BC = AD nên FG = AD. (do BCGF là hình chữ nhật)
Do đó FG = 8 cm.
Do AE = DH nên AE = 6,5 cm. (do AEHD là hình chữ nhật)
Vậy AB = 5 cm; FG = 8 cm và AE = 6,5 cm.
2. Hình lập phương
Khám phá 2 trang 48 Toán lớp 7 Tập 1: Vật nào sau đây có tất cả các mặt đều có dạng hình vuông?
Lời giải:
Ta thấy khối vuông rubik có các mặt đều có dạng hình vuông.
Thực hành 3 trang 49 Toán lớp 7 Tập 1: Quan sát hình lập phương ABCD.A’B’C’D’ có AB = 5 cm (Hình 8).
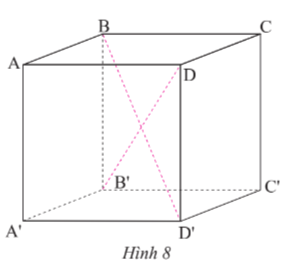
- Tìm độ dài các cạnh BC, CC’.
- Nêu các đường chéo chưa được vẽ.
Lời giải:
- Do ABCD.A’B’C’D’ là hình lập phương nên các cạnh của hình bằng nhau.
Do đó BC = CC’ = AB = 5 cm.
- Các góc ở đỉnh C: ^BCD;^DCC';^BCC'.
- Các đường chéo chưa được vẽ: AC’; CA’.
Lời giải:
Ta thấy các hình trong Hình a đều có dạng hình vuông nên tấm bìa ở hình a gấp được hình lập phương.
Các hình trong Hình b có dạng hình chữ nhật nên tấm bìa ở hình b gấp được hình hộp chữ nhật.
Bài tập
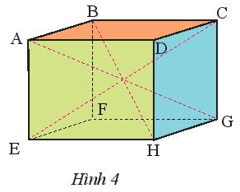
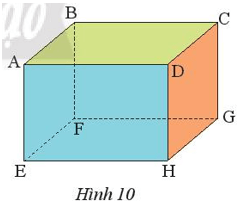
Bài 1 trang 49 Toán lớp 7 Tập 1: Quan sát hình hộp chữ nhật ABCD.EFGH (Hình 10).
a) Nêu các cạnh và đường chéo.
b) Nêu các góc ở đỉnh B và đỉnh C.
c) Kể tên những cạnh bằng nhau.
Lời giải:
a) Các cạnh: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH.
Các đường chéo: AG, BH, CE, DF.
b) Các góc ở đỉnh B: ^ABC;^ABF;^CBF.
Các góc ở đỉnh C: ^BCD;^BCG;^DCG.
c) Các cạnh bằng nhau: AB = CD = EF = GH; BC = AD = HE = FG;
AE = BF = CG = DH.
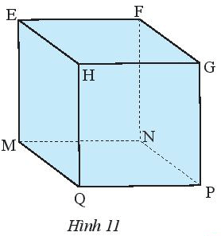
Bài 2 trang 49 Toán lớp 7 Tập 1: Quan sát hình lập phương EFGH.MNPQ (Hình 11).
a) Biết MN = 3 cm. Độ dài các cạnh EF, NF bằng bao nhiêu?
b) Nêu tên các đường chéo của hình lập phương.
Lời giải:
a) Do EFGH.MNPQ là hình lập phương nên các cạnh của hình bằng nhau.
Do đó EF = NF = MN = 3 cm.
b) Các đường chéo của hình lập phương là: EP, FQ, GM, HN.
Lời giải:
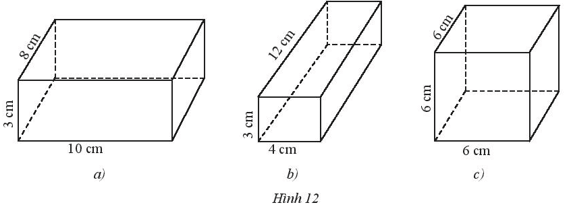
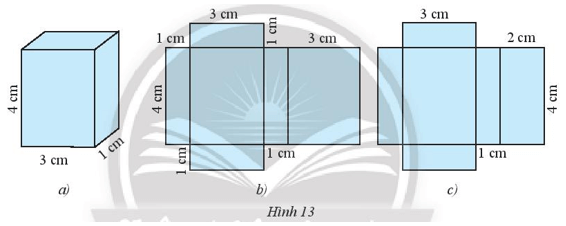
Hình a) các mặt đều là hình chữ nhật với số đo các cạnh không bằng nhau nên hình a) là hình hộp chữ nhật.
Hình b) các mặt đều là hình chữ nhật với số đo các cạnh không bằng nhau nên hình b) là hình hộp chữ nhật.
Hình c) các mặt đều là hình vuông với số đo các cạnh bằng nhau nên hình c) là hình lập phương.
Lời giải:
Ta thấy tấm bìa ở hình c có cạnh 2 cm mà hình hộp ở hình a không có cạnh 2 cm nên tấm bìa ở hình c không gấp được thành hình hộp chữ nhật ở hình a.
Tấm bìa ở hình b có số đo các cạnh giống với số đo các cạnh của hình hộp chữ nhật ở hình a.
Ta đánh số các hình chữ nhật của tấm bìa Hình 13b) bởi các số 1, 2, 3, 4 như hình vẽ dưới đây:
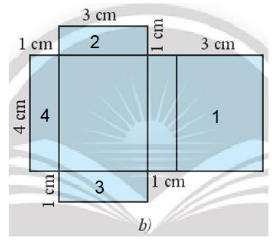
Khi gấp bìa lại thì:
- Chiều dài của hình chữ nhật số 1 trùng với chiều dài của hình chữ nhật số 4.
- Hai chiều rộng của hình chữ nhật số 1 trùng với chiều dài của hai hình chữ nhật số 2 và số 3.
Vậy, tấm bìa hình 13b có thể gấp được hình hộp chữ nhật ở Hình 13a.
Lý thuyết Hình hộp chữ nhật. Hình lập phương
1. Hình hộp chữ nhật
Hình hộp chữ nhật (Hình a) có 6 mặt là hình chữ nhật gồm hai mặt đáy (mặt 1 và mặt 2), và bốn mặt bên (mặt 3, mặt 4, mặt 5 và mặt 6).
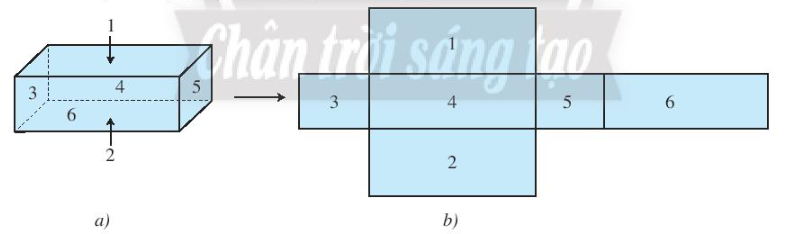
Ví dụ:
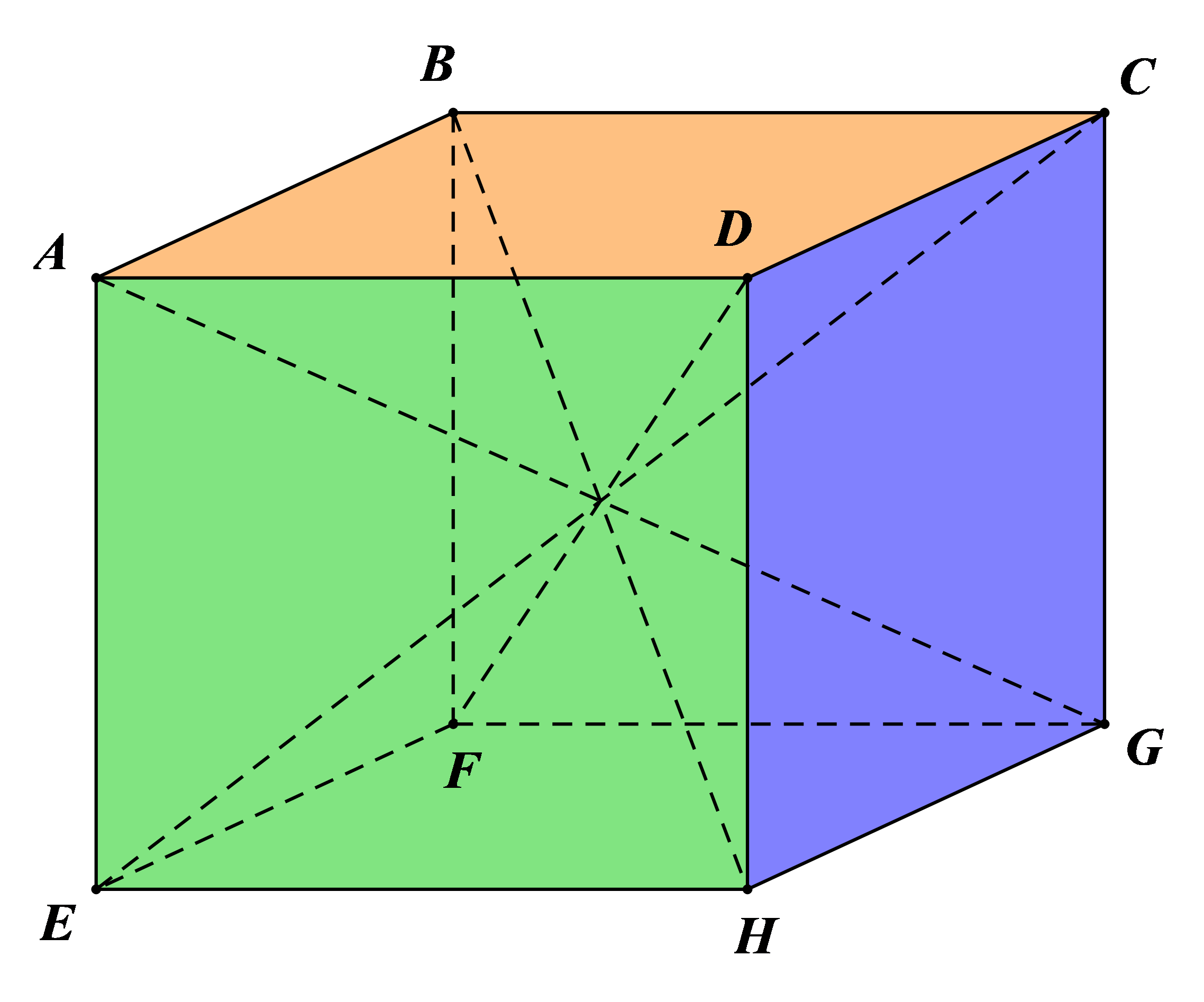
Hình hộp chữ nhật ABCD. EFGH (hình vẽ trên) có:
– Tám đỉnh: A, B, C, D, E, F, G, H.
– Mười hai cạnh: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH.
– Ba góc vuông ở mỗi đỉnh. Chẳng hạn, 3 góc vuông ở đỉnh A: góc EAD, góc EAB, góc BAD.
– Bốn đường chéo: AG, BH, CE, DF.
2. Hình lập phương
Hình lập phương có 6 mặt đều là hình vuông.
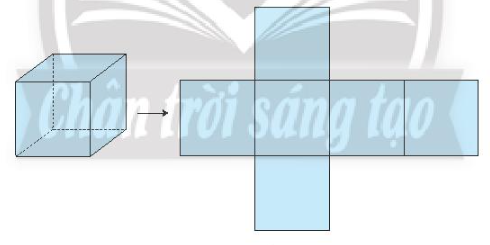
Ví dụ:
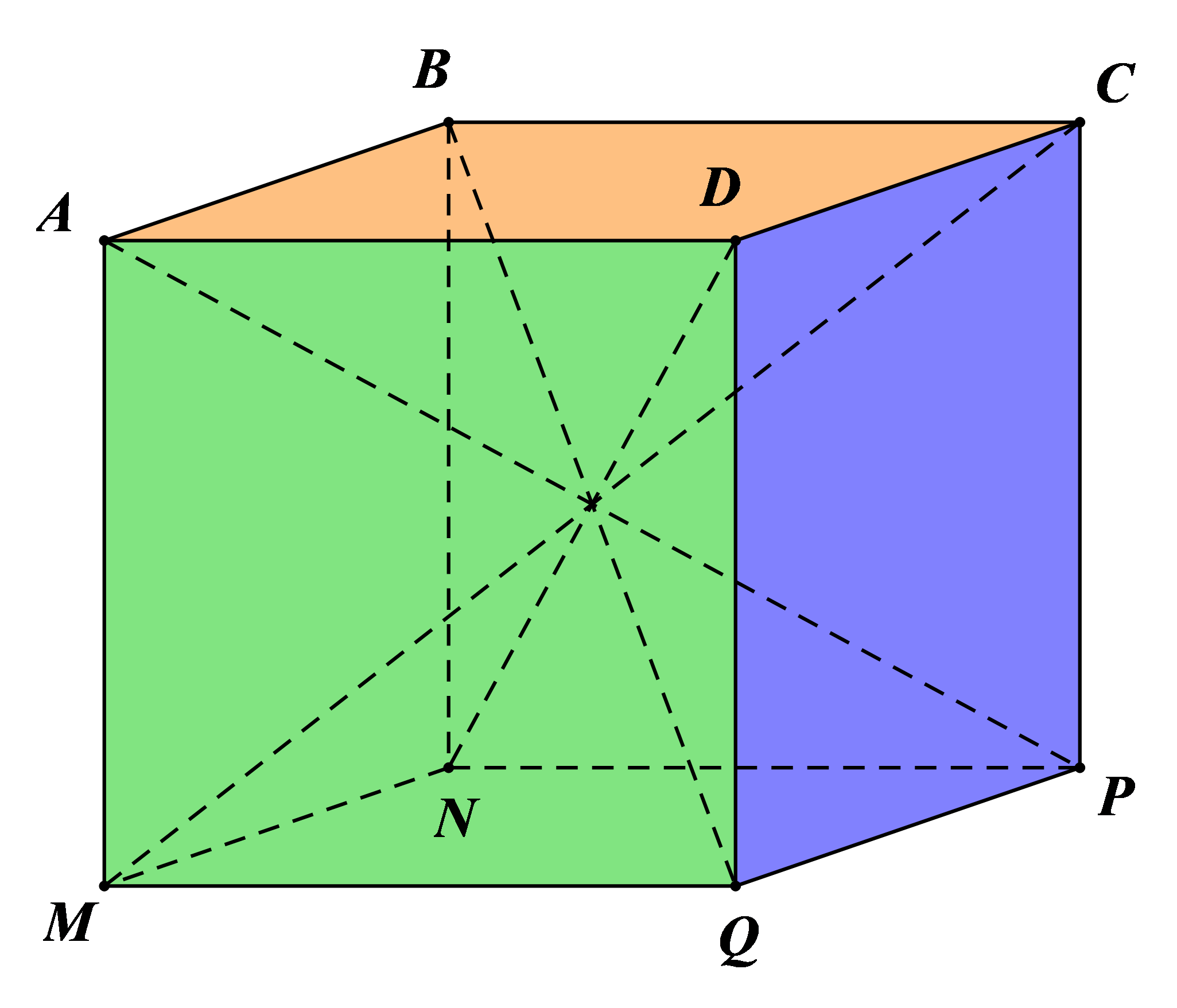
Hình lập phương ABCD. MNPQ có:
– Tám đỉnh: A, B, C, D, M, N, P, Q.
– Mười hai cạnh bằng nhau: AB, BC, CD, DA, MN, NP, PQ, QM, AM, BN, CP, DQ.
– Ba góc vuông ở mỗi đỉnh. Chẳng hạn, 3 góc vuông ở đỉnh A: góc MAD, góc MAB, góc BAD.
– Bốn đường chéo: AP, BQ, CM, DN.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương
Bài 3: Hình lăng trụ đứng tam giác - Hình lăng trụ đứng tứ giác
Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
Bài 5: Hoạt động thực hành và trải nghiệm: Các bài toán về đo đạc và gấp hình
Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 7 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Soạn văn lớp 7 (ngắn nhất) – Chân trời sáng tạo
- Văn mẫu lớp 7 – Chân trời sáng tạo
- Giải sgk Lịch sử 7 – Chân trời sáng tạo
- Lý thuyết Lịch Sử 7 – Chân trời sáng tạo
- Giải sbt Lịch sử 7 – Chân trời sáng tạo
- Giải sgk Địa lí 7 – Chân trời sáng tạo
- Lý thuyết Địa Lí 7 – Chân trời sáng tạo
- Giải sbt Địa lí 7 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 7 Friend plus – Chân trời sáng tạo
- Giải sbt Tiếng Anh 7 Friend plus– Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 7 Friends plus đầy đủ nhất
- Bài tập Tiếng Anh 7 Friends plus theo Unit có đáp án
- Giải sgk Khoa học tự nhiên 7 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 7 – Chân trời sáng tạo
- Giải sbt Khoa học tự nhiên 7 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 7 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 7 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 7 – Chân trời sáng tạo
- Giải sgk Công nghệ 7 – Chân trời sáng tạo
- Lý thuyết Công nghệ 7 – Chân trời sáng tạo
- Giải sbt Công nghệ 7 – Chân trời sáng tạo
- Giải sgk Tin học 7 – Chân trời sáng tạo
- Lý thuyết Tin học 7 – Chân trời sáng tạo
- Giải sbt Tin học 7 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 7 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 7 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 7 – Chân trời sáng tạo
- Giải sgk Âm nhạc 7 – Chân trời sáng tạo