Toán 7 Bài 3 (Chân trời sáng tạo): Hình lăng trụ đứng tam giác - Hình lăng trụ đứng tứ giác

Giải bài tập Toán 7 Bài 3: Hình lăng trụ đứng tam giác - Hình lăng trụ đứng tứ giác

Video giải bài tập Toán 7 Bài 3: Hình lăng trụ đứng tam giác - Hình lăng trụ đứng tứ giác

Hoạt động khởi động

Giải Toán 7 trang 55 Tập 1

Khởi động trang 55 Toán lớp 7 Tập 1: Quan sát lăng kính, hộp đèn và hộp quà ở hình bên dưới. Cho biết các mặt bên của chúng ta là các hình gì.

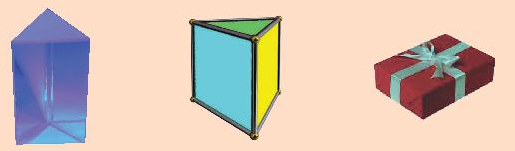
Lời giải:

Mặt bên của lăng kính, hộp đèn và hộp quà trong hình là hình chữ nhật.

1. Hình lăng trụ đứng tam giác, Hình lăng trụ đứng tứ giác

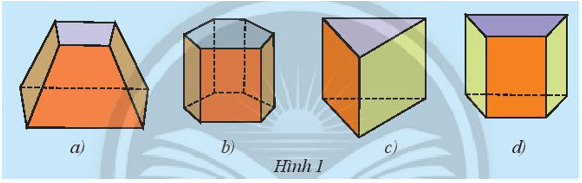
Khám phá trang 55 Toán lớp 7 Tập 1: Hình nào sau đây có:

a) Các mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác?

b) Các mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác?

Lời giải:

a) Hình có mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác là: hình c.

b) Hình có mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác là: hình d.

Giải Toán 7 trang 56 Tập 1

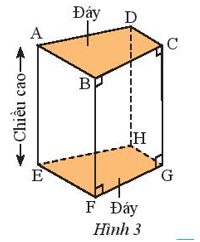
Thực hành 1 trang 56 Toán lớp 7 Tập 1: Quan sát hình lăng trụ đứng tứ giác trong Hình 3.

a) Hãy chỉ ra các mặt đáy và mặt bên của lăng trụ đứng tứ giác.

b) Cạnh bên AE bằng các cạnh nào?

Lời giải:

a) Các mặt đáy: ABCD, EFGH.

Các mặt bên: ADHE, DCGH, CBFG, BAEF.

b) Cạnh bên AE = BF = CG = DH.

Vận dụng 1 trang 56 Toán lớp 7 Tập 1: Hộp kẹo sôcôla (Hình 4a) được vẽ lại như Hình 4b có dạng hình lăng trụ đứng. Hãy chỉ rõ mặt đáy, mặt bên, cạnh bên của hình lăng trụ đó.

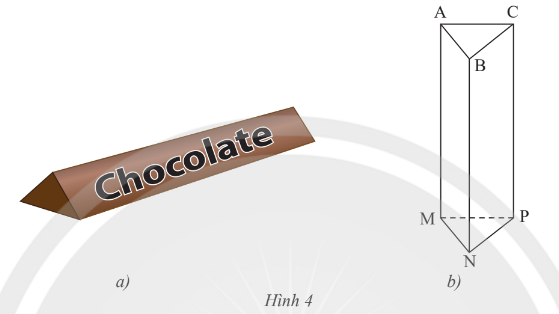
Lời giải:

Mặt đáy: ABC, MNP.

Mặt bên: ABNM, BCPN, ACPM.

Cạnh bên: AM, BN, CP.

2. Tạo lập hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

Thực hành 2 trang 56 Toán lớp 7 Tập 1: Tạo lập hình lăng trụ đứng tam giác có kích thước ba cạnh đáy là 2 cm, 3 cm, 4 cm và chiều cao 3,5 cm theo hướng dẫn sau:

- Vẽ ba hình chữ nhật với kích thước như Hình 5a.

- Cắt miếng bìa như hình vẽ rồi gấp theo đường nét đứt, ta được hình lăng trụ đứng tam giác như Hình 5b.

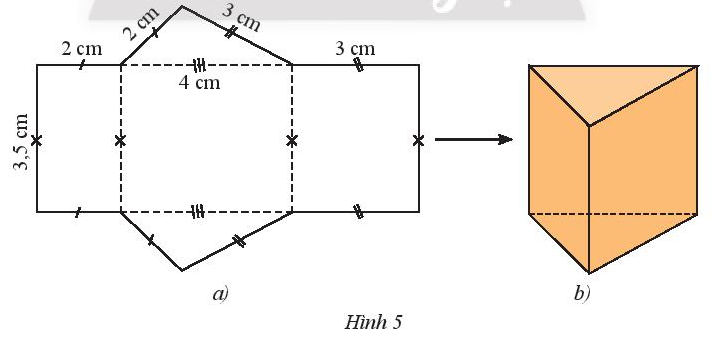
Lời giải:

Học sinh tự thực hiện theo hướng dẫn.

Thực hành 3 trang 56 Toán lớp 7 Tập 1: Tạo lập hình lăng trụ đứng có đáy là hình vuông cạnh 3 cm và chiều cao 5 cm.

Lời giải:

- Trên một miếng bìa, vẽ bốn hình chữ nhật và hai hình vuông với kích thước như hình dưới.

- Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng hình vuông như dưới.

Vận dụng 2 trang 56 Toán lớp 7 Tập 1: Tạo lập hình lăng trụ đứng có đáy là tam giác đều cạnh 3 cm và chiều cao 4 cm.

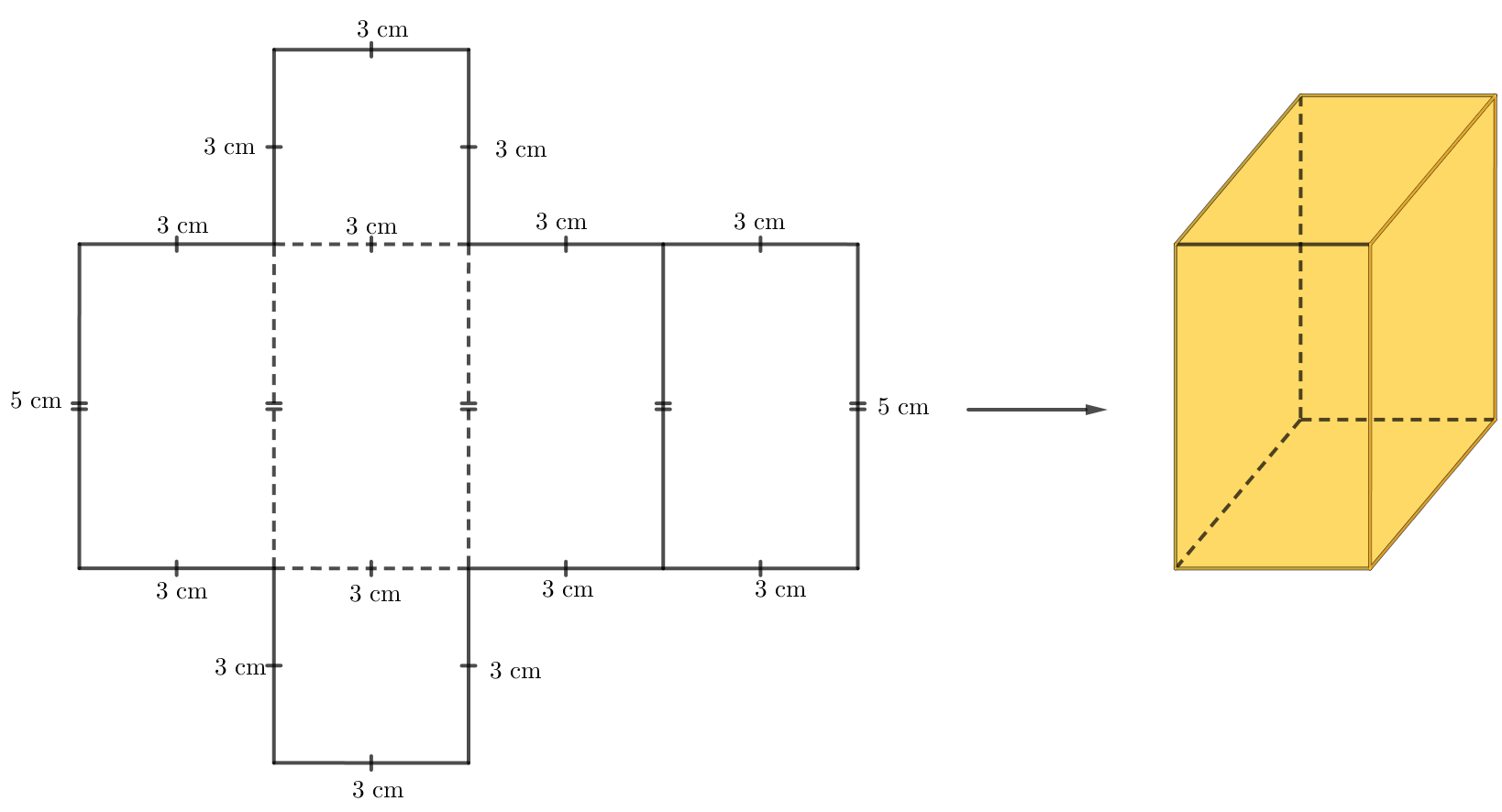
Lời giải:

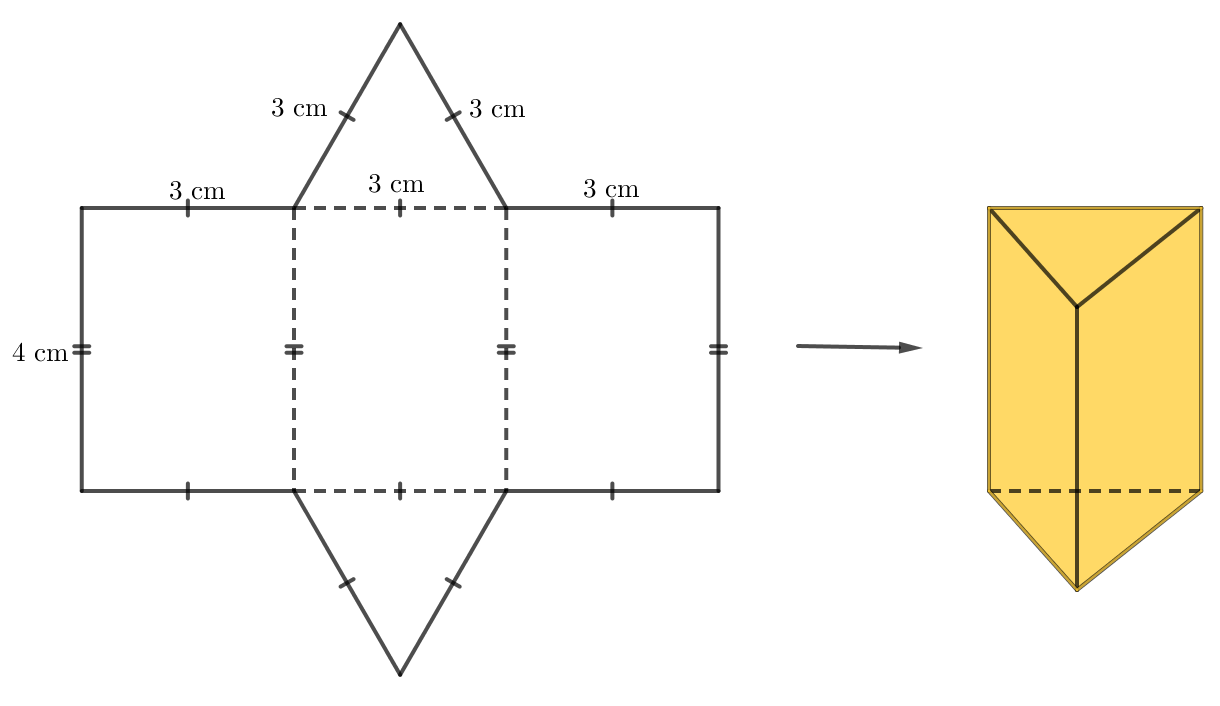
- Trên một miếng bìa, vẽ ba hình chữ nhật và hai tam giác với kích thước như hình dưới.

- Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác như hình dưới.

Bài tập

Giải Toán 7 trang 57 Tập 1

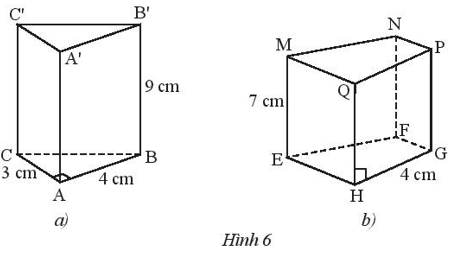
Bài 1 trang 57 Toán lớp 7 Tập 1: Quan sát hai hình lăng trụ đứng trong Hình 6. Tìm độ dài các cạnh:

a) AA’, CC’, A’B’, A’C’ (Hình 6a).

b) QH, PG, NF, PQ (Hình 6b).

Lời giải:

a) Trong Hình 6a:

AA’ = CC’ = BB’ = 9 cm.

A’B’ = AB = 4 cm; A’C’ = AC = 3 cm.

Vậy AA’ = CC’ = 9 cm; A’B’ = 4 cm; A’C’ = 3 cm.

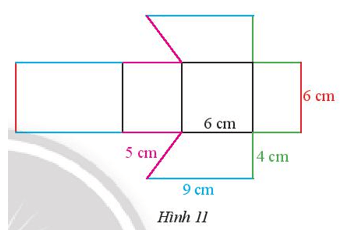
b) Trong Hình 6b:

QH = PG = ME = NF = 7 cm; PQ = HG = 4 cm.

Vậy QH = PG = NF = 7 cm; PQ = 4 cm.

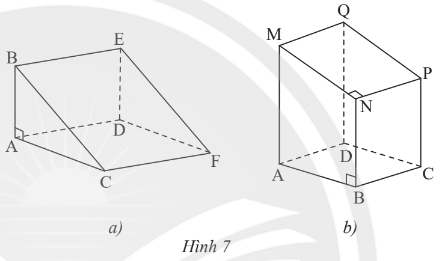
Bài 2 trang 57 Toán lớp 7 Tập 1: Quan sát hình lăng trụ đứng trong Hình 7.

a) Chỉ ra mặt đáy và mặt bên của mỗi hình lăng trụ.

b) Ở Hình 7a, cạnh BE bằng các cạnh nào? Ở Hình 7b, cạnh MQ bằng các cạnh nào?

Lời giải:

a) Xét hình lăng trụ trong Hình 7a:

Mặt đáy: ABC, DEF.

Mặt bên: ADEB, BEFC, ADFC.

Xét hình lăng trụ trong Hình 7b:

Mặt đáy: AMNB, DQPC.

Mặt bên: MNPQ, NBCP, ABCD, MADQ.

b) Ở Hình 7a, cạnh BE = AD = CF.

Ở Hình 7b, cạnh MQ = NP = BC = AD.

Bài 3 trang 57 Toán lớp 7 Tập 1: Tấm bìa ở Hình 8 có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác vuông. Hãy cho biết độ dài hai cạnh góc vuông của đáy và chiều cao của lăng trụ.

Lời giải:

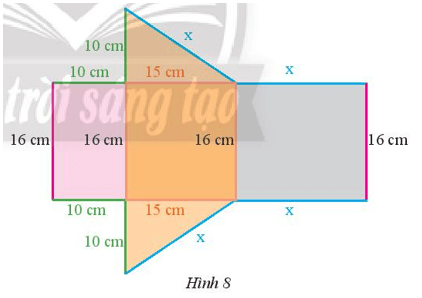
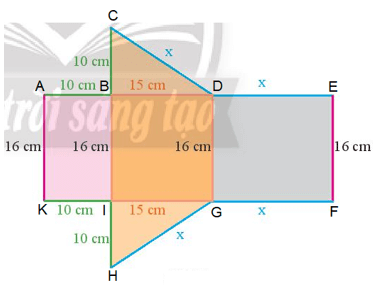
Đặt tên các điểm trong Hình 8 lần lượt là: A, B, C, D, E, F, G, H, I, K (như hình vẽ).

- Gấp các cạnh BI và DG sao cho cạnh AK trùng với cạnh EF.

- Gấp cạnh BD sao cho cạnh AB trùng với cạnh CB, cạnh CD trùng với cạnh ED.

- Gấp cạnh IG sao cho cạnh IK trùng với cạnh IH, cạnh GH trùng với cạnh GF.

Khi đó, ta được hình lăng trụ đứng tam giác ABD.KIG (như hình vẽ).

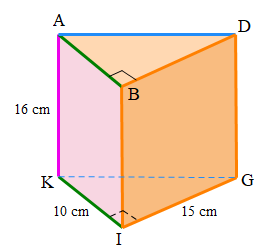
Hình lăng trụ đứng tam giác ABD.KIG có:

- Đáy ABD có hai cạnh góc vuông là AB = 10 cm và BD = 15 cm.

- Đáy KIG có hai cạnh góc vuông là KI = 10 cm và IG = 15 cm.

- Chiều cao của lăng trụ là AK = 16 cm, BI = 16 cm và DG = 16 cm.

Vậy độ dài hai cạnh góc vuông của đáy lần lượt là 10 cm và 15 cm, chiều cao của lăng trụ là 16 cm.

Bài 4 trang 57 Toán lớp 7 Tập 1: Tạo lập hình lăng trụ đứng tam giác với kích thước như Hình 9.

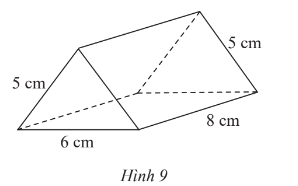
Lời giải:

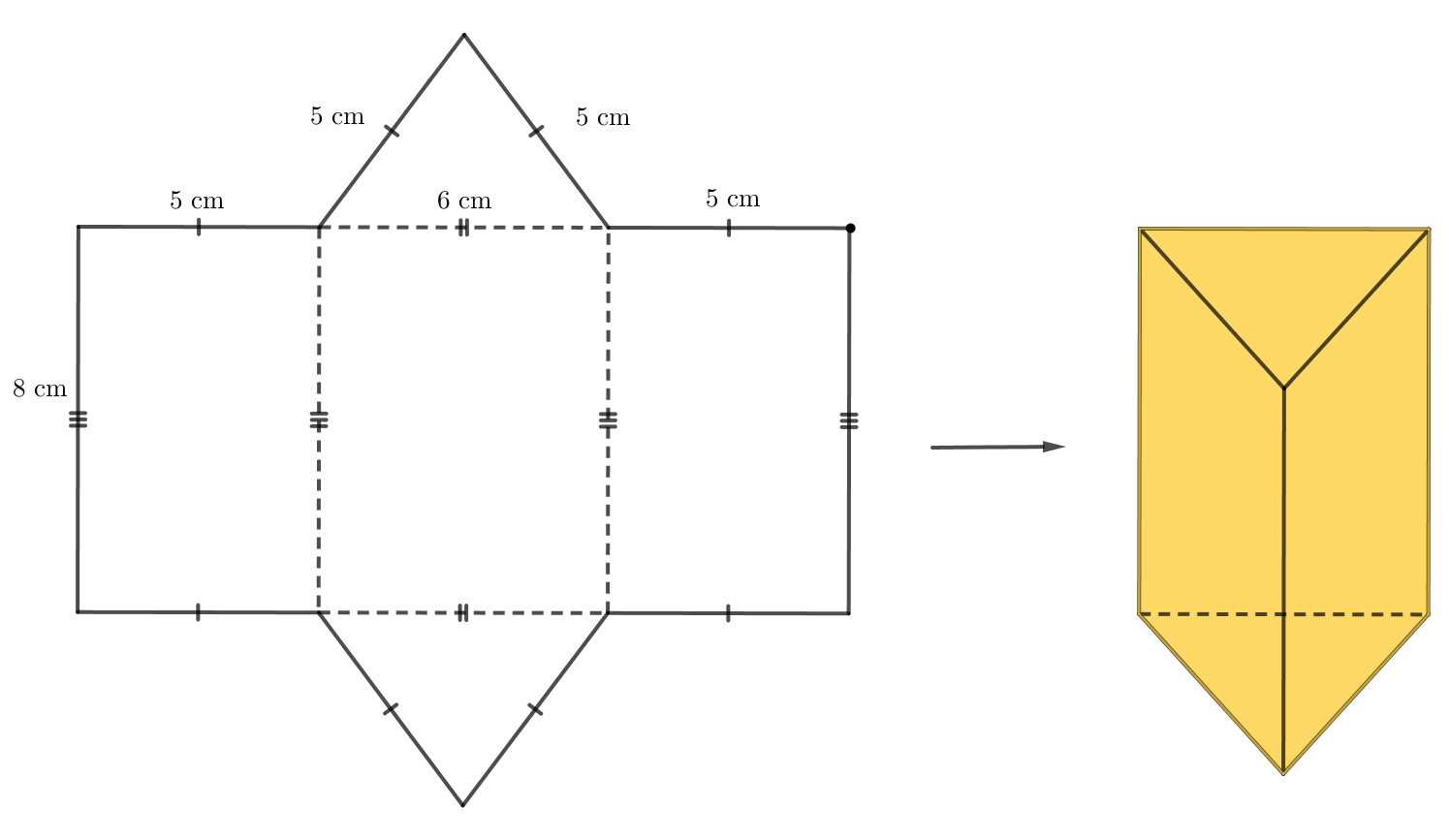
Hình lăng trụ trên có đáy là tam giác có hai cạnh bằng 5 cm và một cạnh bằng 6 cm.

Thực hiện tạo hình lăng trụ đứng như sau:

- Trên một miếng bìa, vẽ ba hình chữ nhật và hai tam giác với kích thước như hình dưới.

- Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác như hình dưới.

Giải Toán 7 trang 58 Tập 1

Bài 5 trang 58 Toán lớp 7 Tập 1: Tạo lập lăng trụ đứng tứ giác có đáy là hình thoi cạnh 5 cm và chiều cao 7 cm (Hình 10).

Lời giải:

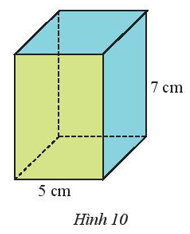
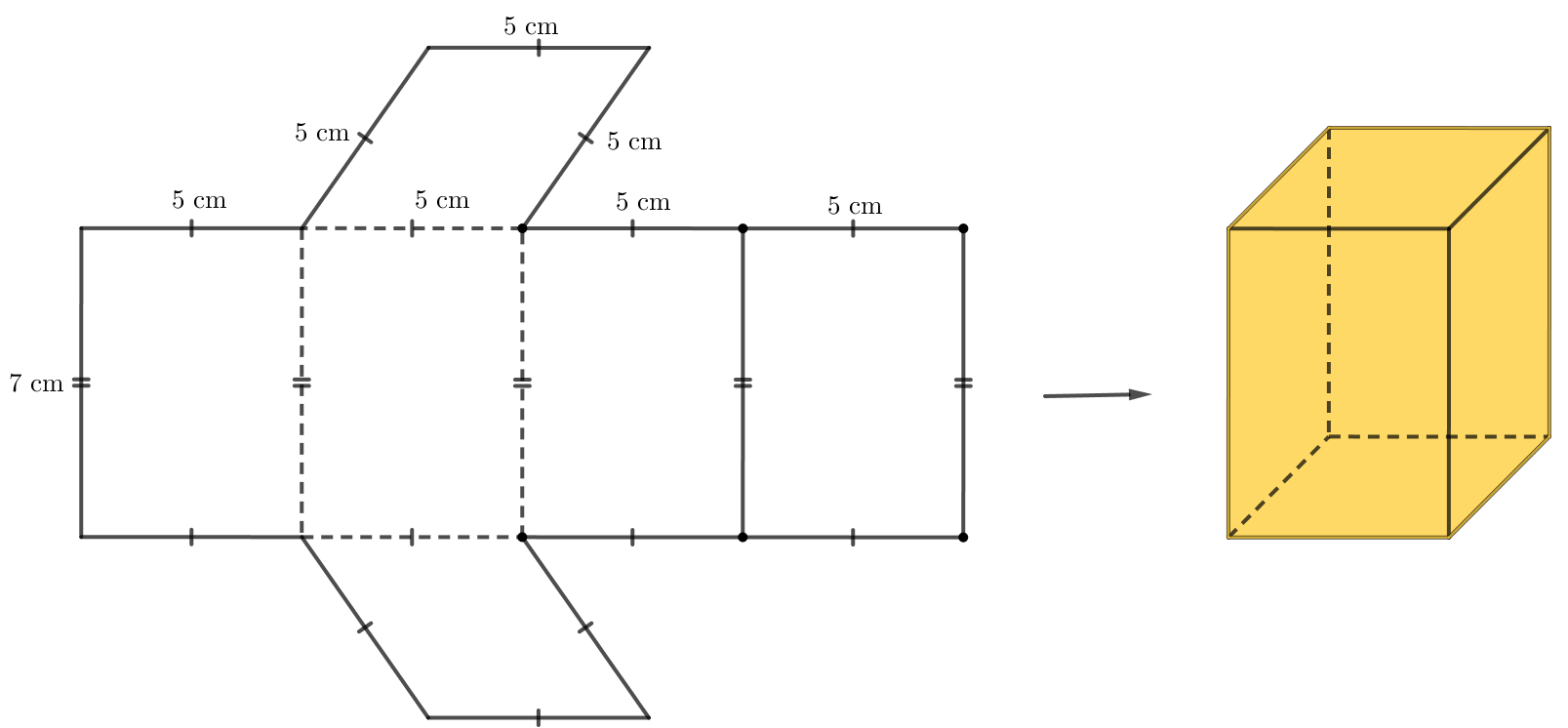
Hình lăng trụ trên có đáy là hình thoi cạnh 5 cm và chiều cao 7 cm.

Thực hiện tạo hình lăng trụ đứng như sau:

- Trên một miếng bìa, vẽ bốn hình chữ nhật và hai hình thoi với kích thước như hình dưới.

- Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng hình thoi như hình dưới.

Bài 6 trang 58 Toán lớp 7 Tập 1: Từ tấm bìa như Hình 11 có thể tạo lập được hình lăng trụ đứng có đáy là hình thang.

Hãy cho biết chiều cao của hình lăng trụ đó.

Lời giải:

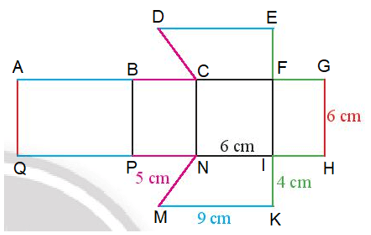
Đặt tên các điểm A, B, C, D, E, F, G, H, I, K, M, N, P, Q (như hình vẽ).

- Gấp các cạnh BP, CN và FI sao cho cạnh AQ trùng với cạnh GH.

- Gấp cạnh CF sao cho cạnh BC trùng với cạnh DC, cạnh AB trùng với cạnh ED, cạnh EF trùng với cạnh GF.

- Gấp cạnh NI sao cho cạnh MN trùng với cạnh PN, cạnh PQ trùng với cạnh MK, cạnh IH trùng với cạnh IK.

Ta có FGHI là hình chữ nhật nên GH = FI = 6 cm.

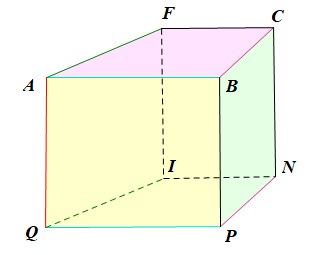
Hình lăng trụ đứng ABCF.QPNI có đáy là hình thang có chiều cao FI = 6 cm.

Vậy hình lăng trụ đứng có đáy là hình thang có chiều cao là 6 cm.

Lý thuyết Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

1. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

– Hình có ba mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác được gọi là hình lăng trụ đứng tam giác.

– Hình có bốn mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác được gọi là hình lăng trụ đứng tứ giác.

Ví dụ:

a) Hình ABC.DEF là hình lăng trụ đứng tam giác.

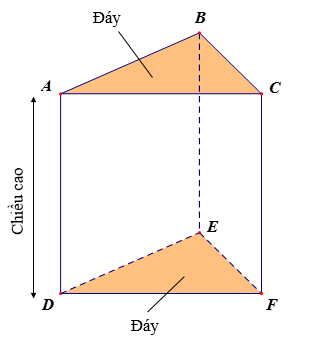
• A, B, C, D, E, F gọi là các đỉnh.

• Ba mặt bên ACFD, BCFE, ABED là các hình chữ nhật.

• Các đoạn thẳng AD, BE, CF bằng nhau và song song với nhau, chúng gọi là các cạnh bên.

• Mặt ABC và mặt DEF song song với nhau và được gọi là hai mặt đáy (gọi tắt là đáy).

• Độ dài cạnh AD được gọi là chiều cao của hình lăng trụ.

b) Hình ABCD.EFGH là hình lăng trụ đứng tứ giác

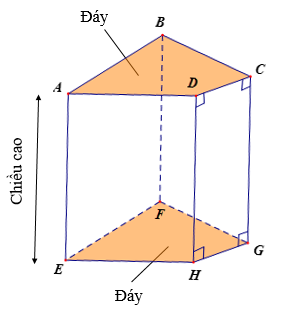
• Hai mặt đáy là tứ giác ABCD và EFGH.

• Các mặt bên ABFE, BCGF, CDHG, ADHE đều là các hình chữ nhật.

Chú ý: Hình hộp chữ nhật, hình lập phương là lăng trụ đứng tứ giác.

2. Tạo lập hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

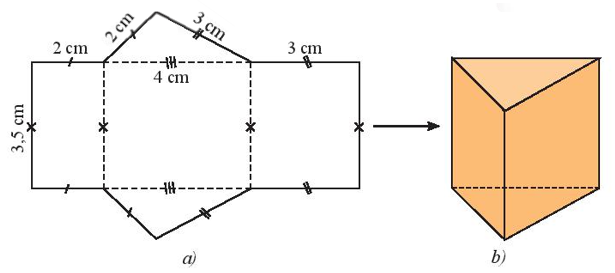
Ví dụ: Tạo lập hình lăng trụ đứng tam giác có kích thước ba cạnh đáy là 2 cm, 3 cm, 4 cm và chiều cao 3,5 cm.

Hướng dẫn giải

– Trên một tấm bìa vẽ ba hình chữ nhật và hai tam giác với kích thước như hình a.

– Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác như hình b.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hình hộp chữ nhật - Hình lập phương

Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

Bài 5: Hoạt động thực hành và trải nghiệm: Các bài toán về đo đạc và gấp hình

Bài tập cuối chương 3

Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 3. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Trắc nghiệm Bài 3. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác