Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 3

Giải bài tập Toán 7 Bài tập cuối chương 3

Bài tập

Giải Toán 7 trang 66 Tập 1

Bài 1 trang 66 Toán lớp 7 Tập 1: Một hình khối gồm 14 hình lập phương gắn kết với nhau như Hình 1. Mỗi hình lập phương có cạnh 1 cm. Hãy tính thể tích của hình khối này.

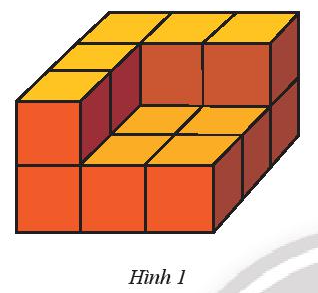
Lời giải:

Thể tích của một hình lập phương là: 1³ = 1 (cm³).

Thể tích của khối hình là: 14 . 1 = 14 (cm³).

Vậy thể tích của khối hình là 14 cm³.

Bài 2 trang 66 Toán lớp 7 Tập 1: Một bể cá hình hộp chữ nhật với kích thước mặt đáy là 5 dm và 12 dm, có mực nước là 7 dm. Người ta đổ vào đó một lượng cát (có độ thấm nước không đáng kể) thì thấy mực nước dâng thêm 1,5 dm và ngập cát đổ vào. Tính thể tích của lượng cát.

Lời giải:

Mực nước sau khi cho cát vào là 7 + 1,5 = 8,5 (dm).

Thể tích của bể cá khi chưa cho cát là: 5 . 12 . 7 = 420 (dm³).

Thể tích của bể cá khi cho cát là: 5 . 12 . 8,5 = 510 (dm³).

Thể tích của lượng cát là: 510 - 420 = 90 (dm³).

Vậy thể tích cát cho vào bể là 90 dm³.

Bài 3 trang 66 Toán lớp 7 Tập 1: Một khuôn đúc bê tông có kích thước như Hình 2. Bể dày các mặt bên của khuôn là 1,2 cm. Bề dày mặt đáy của khuôn là 1,9 cm. Thể tích của khối bê tông được khuôn này đúc ra là bao nhiêu xăngtimét khối?

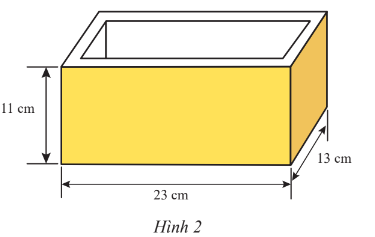
Lời giải:

Do bề dày các mặt bên của khuôn là 1,2 cm nên chiều rộng của mặt đáy khối bê tông được đúc ra là 13 - 1,2 - 1,2 = 10,6 (cm); chiều dài của mặt đáy khối bê tông được đúc ra là 23 - 1,2 - 1,2 = 20,6 (cm).

Do bề dày mặt đáy của khuôn là 1,9 cm nên chiều cao của khối bê tông được đúc ra là

11 - 1,9 = 9,1 (cm).

Thể tích của khối bê tông là:

10,6 . 20,6 . 9,1 = 218,36 . 9,1 = 1987,076 (cm³).

Vậy thể tích của khối bê tông là 1987,076 cm³.

Bài 4 trang 66 Toán lớp 7 Tập 1: Phần bên trong của một cái khuôn làm bánh có dạng hình hộp chữ nhật với đáy là hình vuông cạnh 20 cm, chiều cao 5 cm (Hình 3). Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được 100 m² thì sơn được bao nhiêu cái khuôn làm bánh?

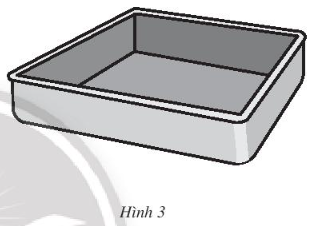
Lời giải:

Diện tích xung quanh của khuôn là: 2 . (20 + 20) . 5 = 400 (cm²).

Diện tích đáy của khuôn là: 20² = 400 (cm²).

Diện tích sơn của một khuôn gồm diện tích xung quanh và diện tích đáy của khuôn.

Diện tích sơn của một khuôn là: 400 + 400 = 800 (cm²).

Đổi 800 cm² = 0,08 m².

Vậy với một lượng sơn đủ bao phủ được 100 m² thì sơn được 100 : 0,08 = 1250 cái khuôn.

Bài 5 trang 66 Toán lớp 7 Tập 1: Một ngôi nhà có kích thước như Hình 4.

a) Tính thể tích của ngôi nhà.

b) Biết rằng 1 l sơn bao phủ được 4 m² tường. Hỏi phải cần ít nhất bao nhiêu lít sơn để sơn phủ được tường mặt ngoài ngôi nhà (không sơn cửa)? Biết tổng diện tích các cửa là 9 m².

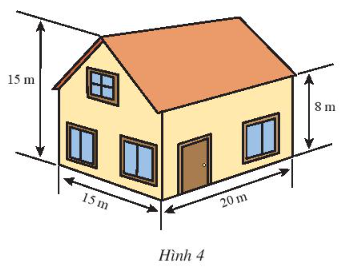
Lời giải:

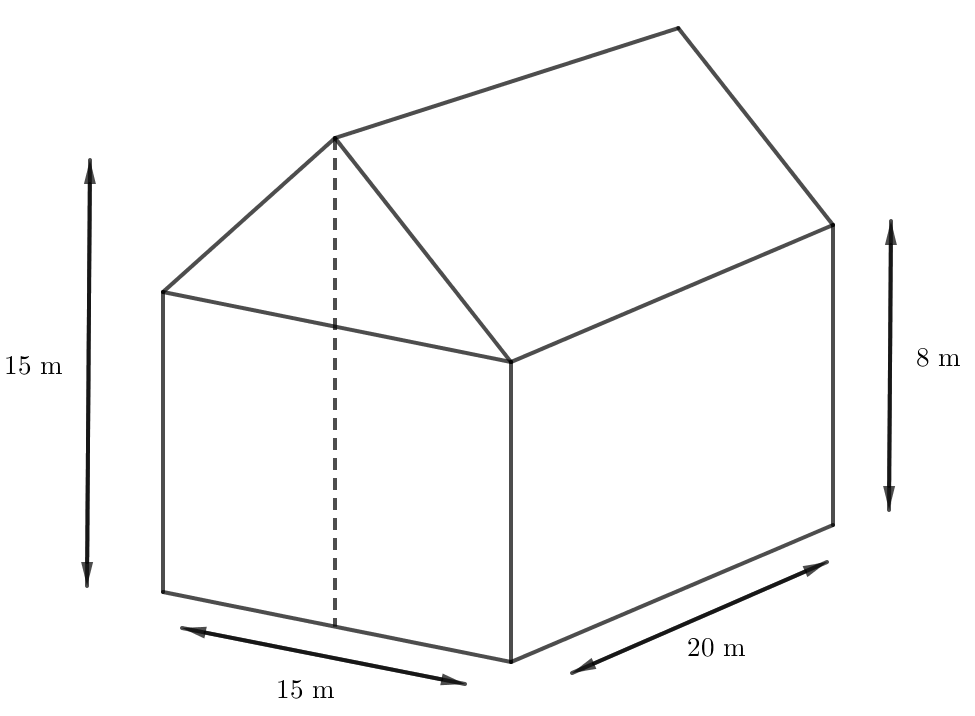
Ngôi nhà trên là hình lăng trụ đứng có đáy được chia thành hai hình thang có độ dài hai đáy lần lượt là 8 m và 15 m; chiều cao của hình thang là 15 : 2 = 7,5 m.

Do đó diện tích đáy bằng 2 lần diện tích hình thang vừa chia.

a) Diện tích hình thang là:

$\frac{\left(8+15\right).7,5}{2}$ = 86,25 (m²).

Diện tích mặt có ba cửa sổ của ngôi nhà là:

2 . 86,25 = 172,5 (m²).

Thể tích của ngôi nhà là: 172,5 . 20 = 3450 (m³).

b) Diện tích mặt trước và mặt sau của ngôi nhà là:

2 . 20 . 8 = 320 (m²).

Tổng diện tích xung quanh của ngôi nhà là: 320 + 2 . 172,5 = 665 (m²).

Do tổng diện tích các cửa là 9 m² nên diện tích cần sơn là: 665 - 9 = 656 (m²).

Cần số lít sơn để phủ được hết mặt ngoài ngôi nhà là:

656 : 4 = 164 (l).

Vậy cần 164 l sơn để phủ được hết mặt ngoài ngôi nhà.

Giải Toán 7 trang 67 Tập 1

Bài 6 trang 67 Toán lớp 7 Tập 1: Các hình hộp chữ nhật trong Hình 5 có cùng số đo thể tích. Em hãy tìm các kích thước còn thiếu.

Lời giải:

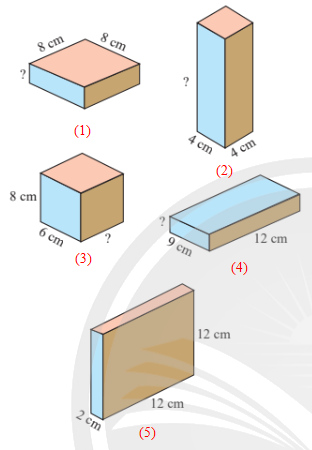
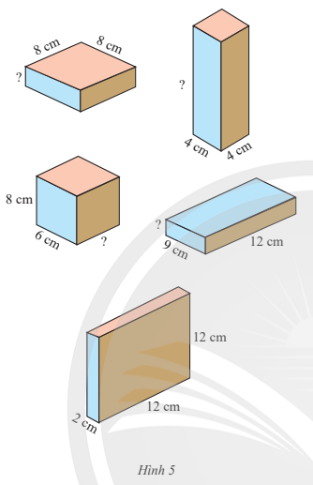
Thể tích của mỗi hình trong Hình 5 là:

2 . 12 . 12 = 288 (cm³).

Kích thước còn thiếu trong hình (1) là: 288 : 8 : 8 = 36 : 8 = 4,5 (cm).

Kích thước còn thiếu trong hình (2) là: 288 : 4 : 4 = 72 : 4 = 18 (cm).

Kích thước còn thiếu trong hình (3) là: 288 : 8 : 6 = 36 : 6 = 6 (cm).

Kích thước còn thiếu trong hình (4) là: 288 : 12 : 9 = 24 : 9 = $\frac{8}{3}$ (cm).

Bài 7 trang 67 Toán lớp 7 Tập 1: Tạo lập hình lăng trụ đứng có chiều cao 2,5 cm, đáy là hình thoi có cạnh 3 cm và một góc 60^o.

Lời giải:

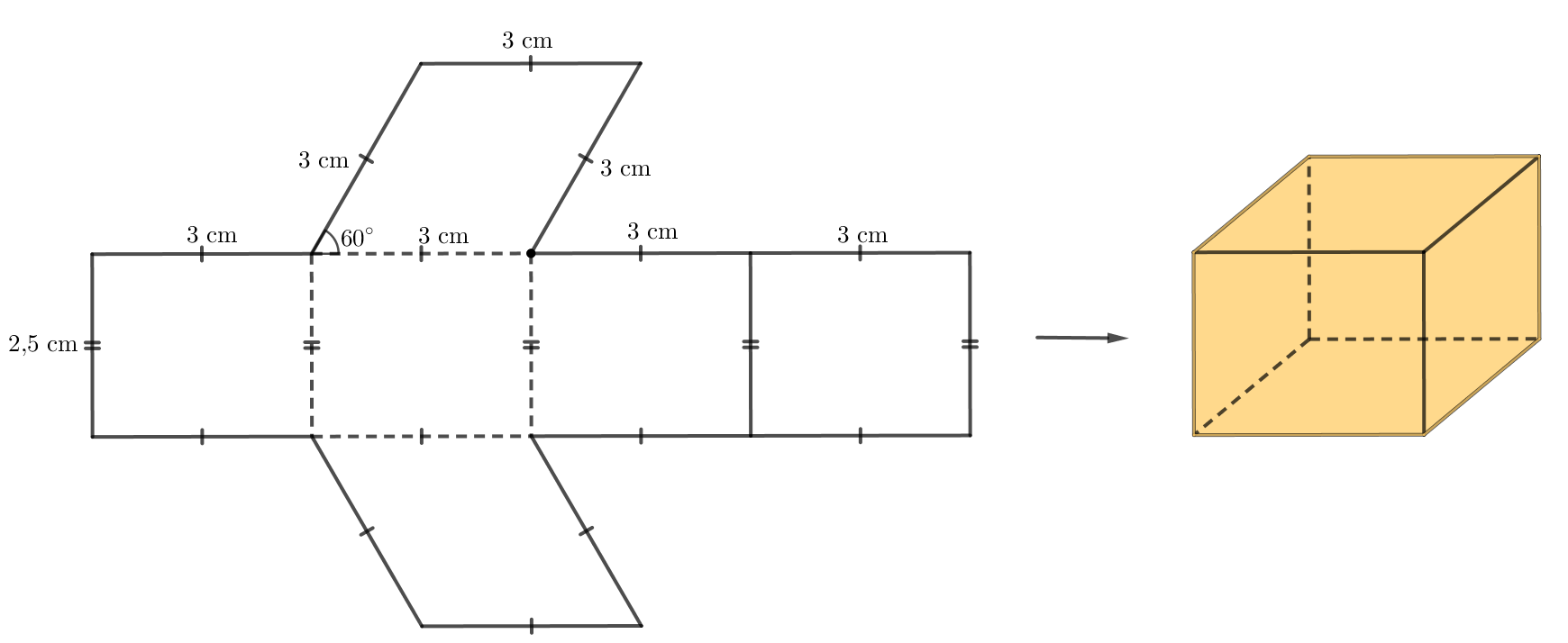
Thực hiện tạo hình lăng trụ đứng như sau:

Bước 1. Vẽ một đoạn thẳng có độ dài 3 cm.

Bước 2. Tại một đầu mút của đoạn thẳng, vẽ đường tròn có bán kính bằng 3 cm và vẽ một đoạn thẳng sao cho đoạn thẳng đó tạo với đoạn thẳng ban đầu một góc 60^o.

- Trên một miếng bìa, vẽ bốn hình chữ nhật và hai hình thoi với kích thước như hình dưới.

- Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng hình thoi như hình dưới.

Bài 8 trang 67 Toán lớp 7 Tập 1: Hãy nêu các bước tạo lập hình lăng trụ đứng tam giác trong Hình 6.

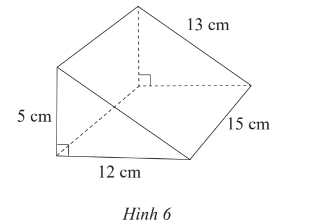
Lời giải:

Trên một miếng bìa, ta thực hiện tạo hình lăng trụ đứng như sau:

Bước 1. Vẽ đoạn thẳng có độ dài 13 cm.

Bước 2. Tại 2 điểm mút của đoạn thẳng, lần lượt vẽ hai đường tròn có bán kính 5 cm và 12 cm. Hai đường tròn này cắt nhau tại một điểm.

Nối điểm đó với hai đầu mút của đoạn thẳng, ta được tam giác vuông có độ dài 3 cạnh lần lượt là 5 cm; 12 cm và 13 cm.

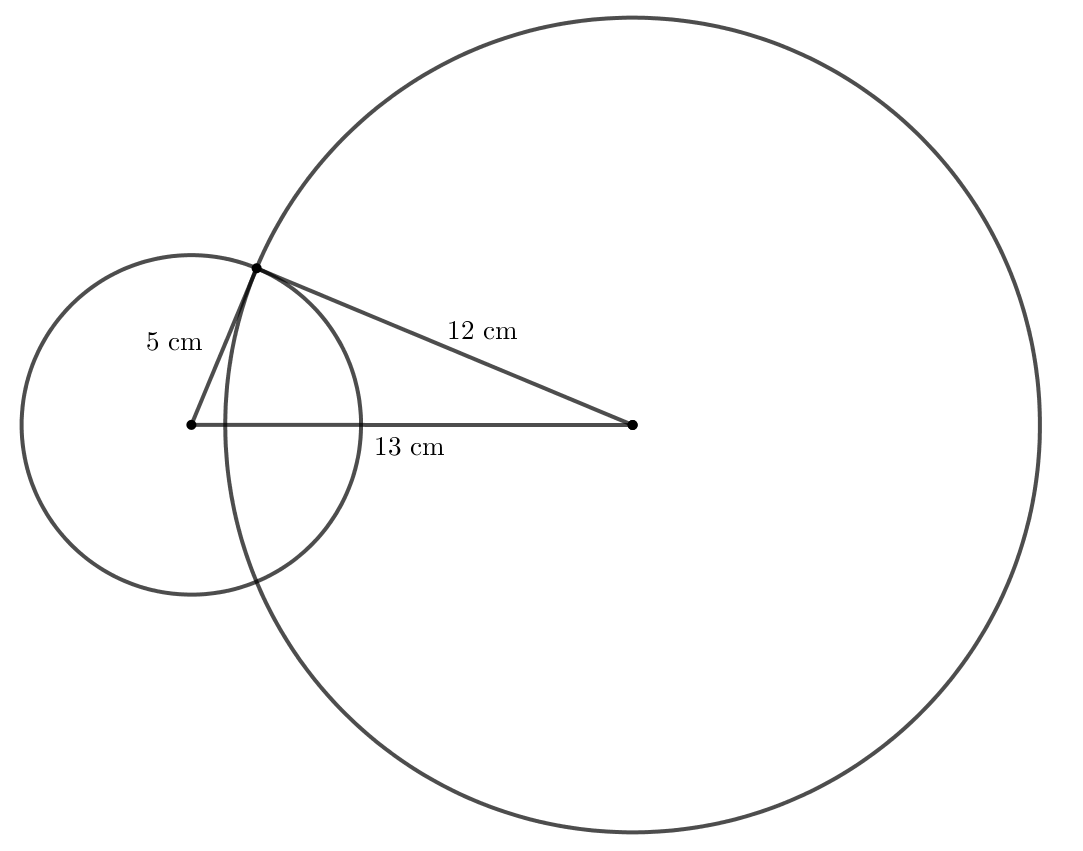
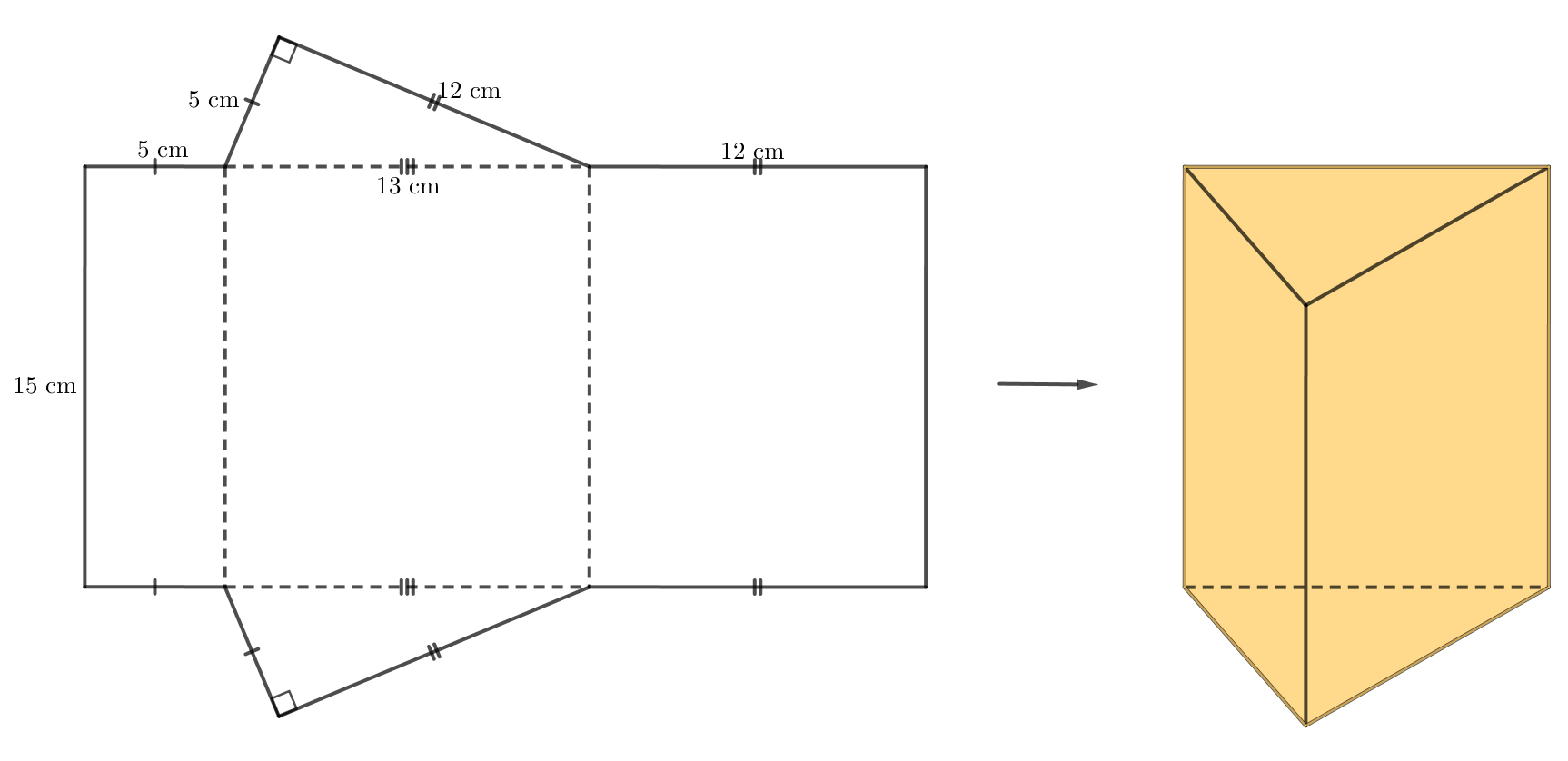
Bước 3. Sau đó thực hiện vẽ thêm ba hình chữ nhật và một tam giác vuông như hình dưới.

Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác vuông như hình dưới.

Bài 9 trang 67 Toán lớp 7 Tập 1: Người ta cắt một tấm bìa để tạo lập một lăng trụ đứng có đáy là tam giác đều với kích thước như Hình 7. Hãy cho biết độ dài các cạnh đáy và chiều cao của hình lăng trụ đứng đó.

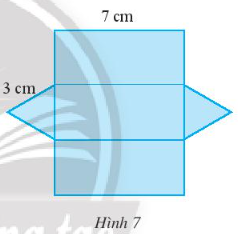
Lời giải:

Độ dài các cạnh đáy của hình lăng trụ là 3 cm.

Độ dài chiều cao của hình lăng trụ đứng là 7 cm.

Vậy hình lăng trụ đứng có đáy là tam giác đều có độ dài mỗi cạnh đáy đều bằng 3 cm và chiều cao là 7 cm.

Lý thuyết Ôn tập chương 3

1. Hình hộp chữ nhật

Hình hộp chữ nhật (Hình a) có 6 mặt là hình chữ nhật gồm hai mặt đáy (mặt 1 và mặt 2), và bốn mặt bên (mặt 3, mặt 4, mặt 5 và mặt 6).

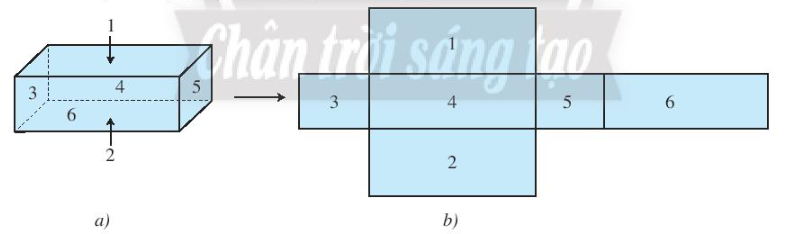
Ví dụ:

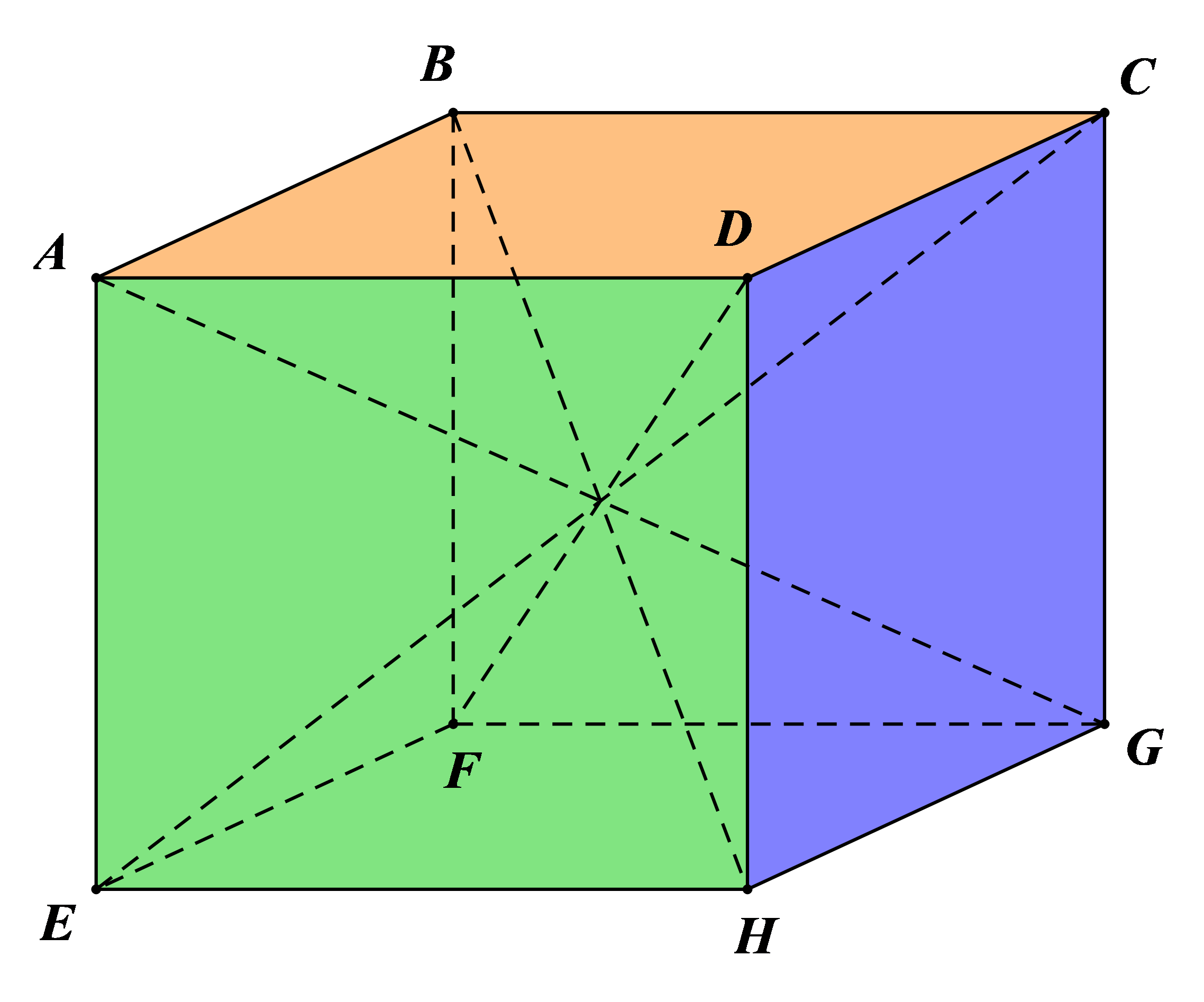
Hình hộp chữ nhật ABCD. EFGH (hình vẽ trên) có:

– Tám đỉnh: A, B, C, D, E, F, G, H.

– Mười hai cạnh: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH.

– Ba góc vuông ở mỗi đỉnh. Chẳng hạn, 3 góc vuông ở đỉnh A: góc EAD, góc EAB, góc BAD.

– Bốn đường chéo: AG, BH, CE, DF.

2. Hình lập phương

Hình lập phương có 6 mặt đều là hình vuông.

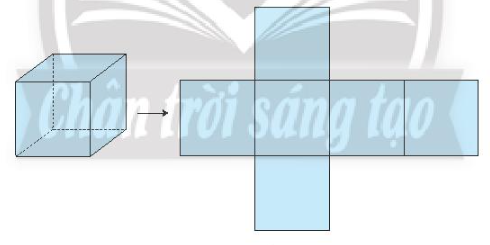
Ví dụ:

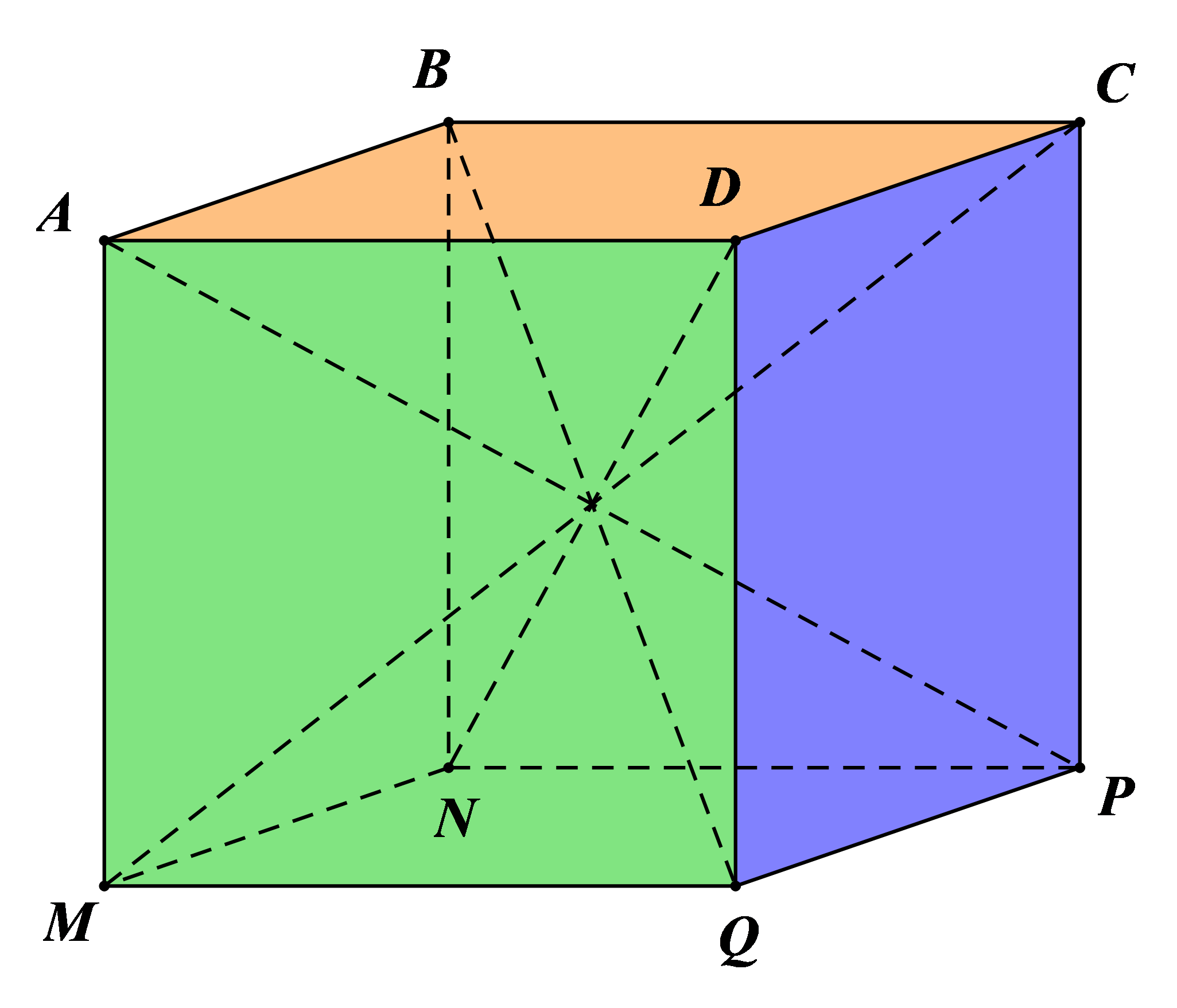
Hình lập phương ABCD. MNPQ có:

– Tám đỉnh: A, B, C, D, M, N, P, Q.

– Mười hai cạnh bằng nhau: AB, BC, CD, DA, MN, NP, PQ, QM, AM, BN, CP, DQ.

– Ba góc vuông ở mỗi đỉnh. Chẳng hạn, 3 góc vuông ở đỉnh A: góc MAD, góc MAB, góc BAD.

– Bốn đường chéo: AP, BQ, CM, DN.

B. Bài tập tự luyện

B.1. Bài tập trắc nghiệm

Câu 1. Mảnh bìa dưới đây có thể gấp thành hình gì?

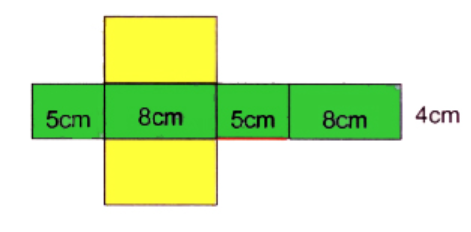
A. Hình lập phương;

B. Hình hộp chữ nhật;

C. Hình chữ nhật;

D. Hình thoi.

Hướng dẫn giải

Đáp án đúng là: C

Sau khi gấp miếng bìa đã cho

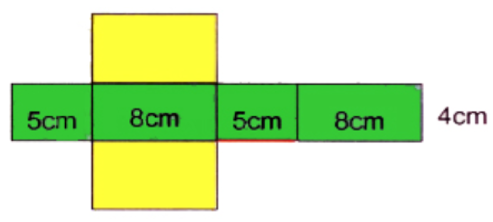
Ta hình hộp chữ nhật như sau:

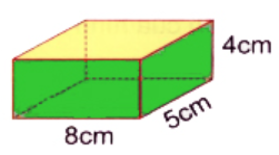
Vậy ta chọn phương án C.

Câu 2. Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?

A. 2 hình lập phương, 3 hình hộp chữ nhật;

B. 1 hình lập phương, 3 hình hộp chữ nhật;

C. 2 hình lập phương, 2 hình hộp chữ nhật;

D. 0 hình lập phương, 4 hình hộp chữ nhật.

Hướng dẫn giải

Đáp án đúng là: D

Quan sát hình ta thấy không có hộp quà có dạng hình lập phương, có 4 hộp quà có dạng hình hộp chữ nhật đó là: hộp quà màu hồng nhạt, hộp quà màu xanh lam, hộp quà màu đỏ, hộp quà màu xanh lá cây.

Vậy chọn phương án D.

Câu 3. Trong các mảnh bìa dưới đây có mấy mảnh bìa có thể gấp thành một hình lập phương?

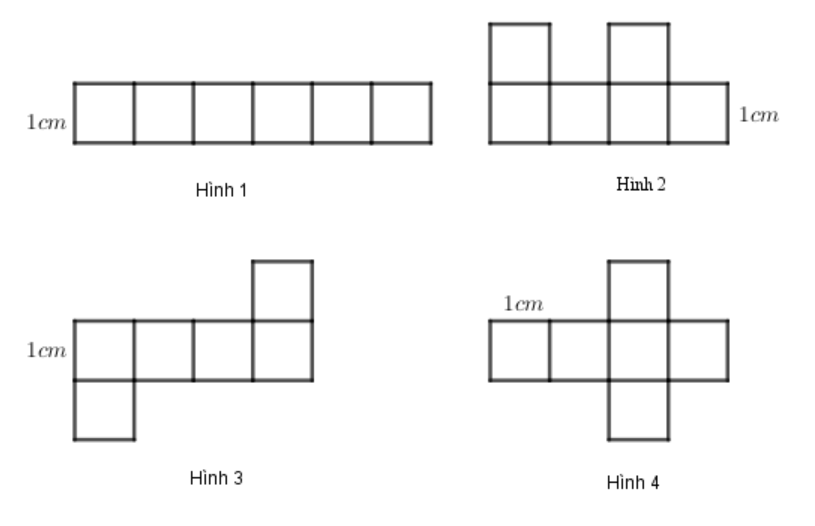
A. 2;

B. 3;

C. 4;

D. 1.

Hướng dẫn giải

Đáp án đúng là: A

Hình 3 và Hình 4 là hai mảnh bìa có thể gấp thành hình lập phương.

Vậy chọn phương án A.

B.2. Bài tập tự luận

Bài 1. Quan sát hình hộp chữ nhật ABCD.MNKH trong hình dưới đây:

a) Nêu các cạnh và đường chéo.

b) Nêu các góc ở đỉnh K và đỉnh H.

c) Kể tên các cạnh bằng nhau.

Hướng dẫn giải

a) Các cạnh của hình hộp chữ nhật ABCD.MNKH là: AB, BC, CD, DA, MN, NK, KH, HM, AM, BN, CK, DH.

Các đường chéo của hình hộp chữ nhật ABCD.MNKH là: AK, BH, CM, DN.

b) Các góc ở đỉnh K là: góc CKH, góc CKN, góc HKN.

Các góc ở đỉnh H là: góc DHM, góc DHK, góc KHM.

c) Các cạnh bằng nhau:

• AB = CD = HK = MN;

• AD = BC = NK = MH;

• AM = BN = CK = DH.

Bài 2. Cho hình lập phương EFGH.MNPQ.

a) Biết PQ = 5 cm. Độ dài các cạnh HG, HQ bằng bao nhiêu?

b) Nêu tên các đường chéo của hình lập phương đó.

Hướng dẫn giải

a) Vì EFGH. MNPQ là hình lập phương nên các cạnh của hình lập phương bằng nhau.

Do đó HQ = HG = PQ = 5 cm.

Vậy HQ = HG = 5 cm.

b) Các đường chéo của hình lập phương EFGH.MNPQ là: EP, FQ, GM, HN.

3. Công thức tính diện tích xung quanh và thể tích

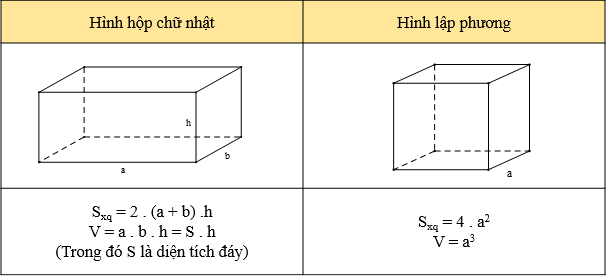
Ví dụ: Diện tích xung quanh và thể tích của hình lập phương có độ dài cạnh là 10 cm lần lượt là:

S_xq = 4 . a² = 4 . 10² = 400 (cm²);

V = a³ = 10³ = 1000 (cm³).

4. Một số bài toán thực tế

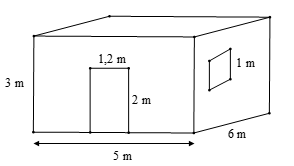
Ví dụ: Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình dưới. Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.

Hướng dẫn giải

Để tính được số tiền bác Long dùng để sơn căn phòng ta phải tính được diện tích phần cần sơn.

Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.

Diện tích xung quanh của căn phòng là:

S_xq = 2. (5 + 6) . 3 = 66 (m²).

Diện tích phần cửa lớn và cửa sổ là:

1,2 . 2 + 1 . 1 = 3,4 (m²)

Diện tích phần cần sơn là:

66 – 3,4 = 62,6 (m²).

Tổng chi phí cần để sơn là:

62,6. 30 000 = 1 878 000 (đồng).

Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.

Ví dụ: Bạn Ngọc muốn làm một hộp quà hình lập phương có kích thước cạnh là 30 cm bằng tấm bìa. Em hãy tính diện tích phần tấm bìa cần dùng và thể tích của hộp quà.

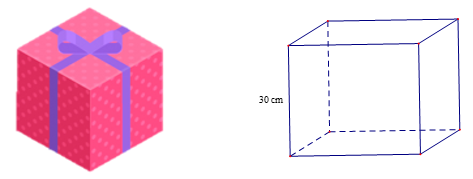
Hướng dẫn giải

Hộp quà hình lập phương nên ta có:

Diện tích tấm bìa cần dùng sẽ bằng diện tích xung quanh của hình lập phương cộng với diện tích hai mặt đáy.

Diện tích xung quanh của hộp quà là:

S_xq = 4 . 30² = 3 600 (cm²).

Diện tích đáy của hình lập phương là:

30 . 30 = 900 (cm²).

Vậy diện tích hai đáy của hình lập phương là:

2. 900 = 1 800 (cm²).

Diện tích tấm bìa cần dùng để làm hộp quà là:

3 600 + 1 800 = 5 400 (cm²).

Thể tích của hộp quà là

V = 30³ = 27 000 (cm³).

Vậy diện tích tấm bìa cần dùng là 5 400 cm² và thể tích của hộp quà là 27 000 cm³.

B. Bài tập tự luyện

B.1. Bài tập trắc nghiệm

Câu 1. Một hình hộp chữ nhật có thể tích 7,5 cm³, chiều dài 2,5 cm và chiều rộng bằng $\frac{3}{5}$ chiều dài. Chiều cao của hình hộp chữ nhật đó là:

A. 1,5 cm;

B. 0,72 cm;

C. 5 cm;

D. 2 cm.

Hướng dẫn giải

Đáp án đúng là: D

Chiều rộng của hình hộp chữ nhật đó là:

2,5 . $\frac{3}{5}$ = 1,5 (cm)

Chiều cao của hình hộp chữ nhật đó là:

7,5 : 1,5 : 2,5 = 2 (cm)

Vậy chiều cao của hình hộp chữ nhật đó là 2 cm.

Câu 2. Độ dài cạnh của hình lập phương có thể tích bằng 729 cm³ là:

A. 9 cm;

B. 10 cm;

C. 27 cm;

D. 3 cm.

Hướng dẫn giải

Đáp án đúng là: A

Gọi độ dài cạnh của hình lập phương là a (cm) (a > 0).

Thể tích của hình lập phương là: V = a³ = 729 (cm³).

Hay a³ = 9³.

Suy ra a = 9 (thỏa mãn).

Vậy độ dài cạnh của hình lập phương là 9 cm.

Câu 3. Một thùng bánh có dạng hình hộp chữ nhật với chiều dài 30 cm, chiều rộng 20 cm và chiều cao 15 cm. Người ta đựng những hộp bánh có dạng hình lập phương có cạnh 10 cm vào trong thùng đó. Hỏi thùng đó đựng được bao nhiêu hộp bánh:

A. 9 hộp;

B. 7 hộp;

C. 10 hộp;

D. 11 hộp.

Hướng dẫn giải

Đáp án đúng là: A

Thể tích của thùng bánh là:

30 . 20 . 15 = 9 000 (cm³)

Thể tích của mỗi hộp bánh là:

10³ = 1 000 (cm³)

Thùng đó đựng được số hộp bánh là:

9 000 : 1 000 = 9 (hộp)

Vậy thùng đó đựng được 9 hộp bánh.

B.2. Bài tập tự luận

Bài 1. Tính diện tích xung quanh và thể tích của hình hộp chữ nhật có chiều dài là 10 cm, chiều rộng là 7 cm và chiều cao là 5 cm.

Hướng dẫn giải

Diện tích xung quanh của hình hộp chữ nhật là:

S_xq = 2 . (10 + 7) . 5 = 170 (cm²).

Thể tích của hình hộp chữ nhật là:

V = 10 . 7 . 5 = 350 (cm³).

Vậy diện tích xung quanh và thể tích của hình hộp chữ nhật lần lượt là 170 cm² và 350 cm³.

Bài 2. Một chiếc bánh kem có dạng hình hộp chữ nhật với chiều dài 30 cm, chiều rộng 20 cm, chiều cao 15 cm. Người ta cắt đi một miếng bánh có dạng hình lập phương cạnh 5 cm. Tính thể tích phần còn lại của chiếc bánh kem.

Hướng dẫn giải

Thể tích của chiếc bánh kem khi chưa bị cắt là:

30 . 20 . 15 = 9 000 (cm³)

Thể tích phần bánh kem bị cắt đi là:

5³ = 125 (cm³).

Thể tích phần còn lại của chiếc bánh kem là:

9 000 – 125 = 8 875 (cm³).

Vậy thể tích phần còn lại của chiếc bánh kem là 8 875 cm³.

5. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

– Hình có ba mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác được gọi là hình lăng trụ đứng tam giác.

– Hình có bốn mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác được gọi là hình lăng trụ đứng tứ giác.

Ví dụ:

a) Hình ABC.DEF là hình lăng trụ đứng tam giác.

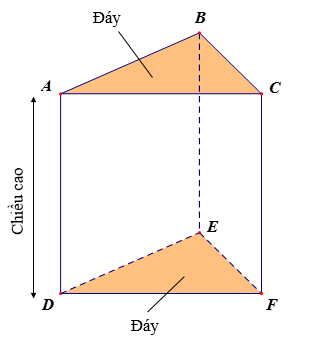
• A, B, C, D, E, F gọi là các đỉnh.

• Ba mặt bên ACFD, BCFE, ABED là các hình chữ nhật.

• Các đoạn thẳng AD, BE, CF bằng nhau và song song với nhau, chúng gọi là các cạnh bên.

• Mặt ABC và mặt DEF song song với nhau và được gọi là hai mặt đáy (gọi tắt là đáy).

• Độ dài cạnh AD được gọi là chiều cao của hình lăng trụ.

b) Hình ABCD.EFGH là hình lăng trụ đứng tứ giác

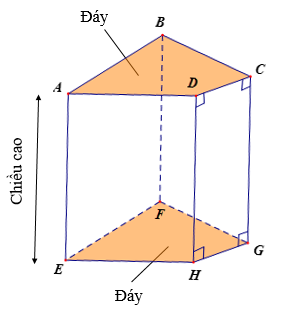
• Hai mặt đáy là tứ giác ABCD và EFGH.

• Các mặt bên ABFE, BCGF, CDHG, ADHE đều là các hình chữ nhật.

Chú ý: Hình hộp chữ nhật, hình lập phương là lăng trụ đứng tứ giác.

6. Tạo lập hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

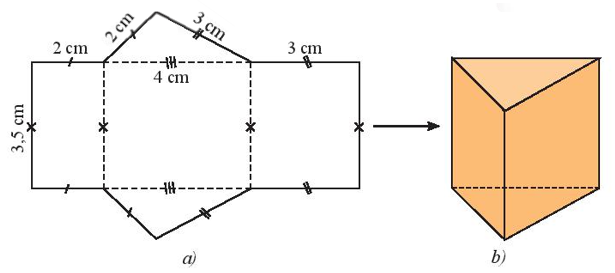
Ví dụ: Tạo lập hình lăng trụ đứng tam giác có kích thước ba cạnh đáy là 2 cm, 3 cm, 4 cm và chiều cao 3,5 cm.

Hướng dẫn giải

– Trên một tấm bìa vẽ ba hình chữ nhật và hai tam giác với kích thước như hình a.

– Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác như hình b.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hình hộp chữ nhật - Hình lập phương

Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Bài 3: Hình lăng trụ đứng tam giác - Hình lăng trụ đứng tứ giác

Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

Bài 5: Hoạt động thực hành và trải nghiệm: Các bài toán về đo đạc và gấp hình

Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Ôn tập chương 3

Trắc nghiệm Ôn tập chương 3