TOP 20 câu Trắc nghiệm Toán lớp 7 (Chân trời sáng tạo 2024) có đáp án: Ôn tập chương 3
Bộ 20 bài tập trắc nghiệm Toán lớp 7 Ôn tập chương 3 có đáp án đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Ôn tập chương 3.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 7 Chân trời sáng tạo bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 033000255833 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 7 Ôn tập chương 3 - Chân trời sáng tạo
I. Nhận biết
Câu 1. Hãy chọn khẳng định sai.
Hình hộp chữ nhật ABCD.A'B'C'D' có:
A. 8 đỉnh;
B. 4 mặt bên;
C. 6 cạnh;
D. 6 mặt.
Đáp án: C
Giải thích:
Hình hộp chữ nhật này có 12 cạnh: AB; BC; CD; DA; A'B'; C'D'; B'C'; D'A'; AA'; BB'; CC'; DD'.
Do đó phương án C là khẳng định sai.
Câu 2. Trong các hình hộp dưới đây hình nào là hình lập phương?
A. 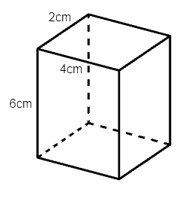
B. 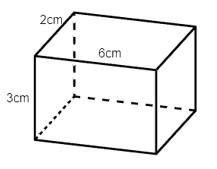
C. 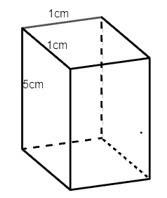
D. 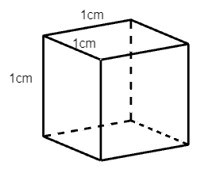
Đáp án: A
Giải thích:
Ta thấy hình D là hình hộp có các cạnh bằng nhau nên hình D là hình lập phương.
Câu 3. Các mặt bên của hình lăng trụ đứng là
A. Hình thoi;
B. Hình tam giác;
C. Hình bình hành;
D. Hình chữ nhật.
Đáp án: D
Giải thích:
Hình lăng trụ có hai đáy là những đa giác và các mặt bên là những hình chữ nhật.
Câu 4. Hình hộp chữ nhật có ba kích thước lần lượt là: a, 2a, 2a. Thể tích của hình hộp chữ nhật đó là:
A. a3;
B. 2a3;
C. 3a3;
D. 4a3.
Đáp án: D
Giải thích:
Thể tích của hình hộp chữ nhật là:
V = a. 2a. 2a = 4a3 (đơn vị thể tích).
Câu 5. Diện tích xung quanh của hình hộp chữ nhật có đáy với kích thước hai cạnh là 2 cm, 3 cm và chiều cao 4 cm là:
A. 10 cm2;
B. 20 cm2;
C. 30 cm2;
D. 40 cm2.
Đáp án: D
Giải thích:
Diện tích xung quanh của hình hộp chữ nhật có đáy với kích thước hai cạnh là 2 cm, 3 cm và chiều cao 4 cm là:
2.(2 + 3).4 = 40 cm2.
Vậy diện tích xung quanh của hình hộp chữ nhật đã cho là 40 cm2.
Câu 6. Cho một hình lăng trụ đứng có diện tích đáy là S, chiều cao là h. Công thức tính thể tích lăng trụ đứng là công thức nào dưới đây:
A. V = S.h;
B. V = 3S.h;
C. ;
D. V = 2S.h.
Đáp án: A
Giải thích:
Công thức tính thể tích lăng trụ đứng là: V = S.h.
Câu 7. Cho một hình lăng trụ đứng có đáy là một tam giác có các kích thước là 3 cm, 4 cm, 5 cm và có chiều cao là 4 cm. Diện tích xung quanh của hình lăng trụ trên là
A. 48 cm2;
B. 24 cm2;
C. 12 cm2;
D. 14 cm2.
Đáp án: A
Giải thích:
Diện tích xung quanh của hình lăng trụ đã cho là:
(3 + 4 + 5).4 = 48 (cm2).
II. Thông hiểu
Câu 1. Cho hình hộp chữ nhật ABCD. EFGH. Chọn khẳng định đúng:
A. AE và BF cắt nhau;
B. ED và HA cắt nhau;
C. EF và GH cắt nhau;
D. AD và BC cắt nhau.
Đáp án: B
Giải thích:
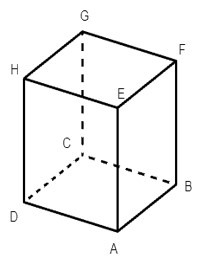
Vì ABCD. EFGH là hình hộp chữ nhật nên ta có:
• AEFB là hình chữ nhật suy ra AE // BF.
Do đó AE và BF không cắt nhau. Vậy A là một khẳng định sai.
• AEHD là hình chữ nhật mà ED và HA là hai đường chéo của hình chữ nhật này nên ED và HA cắt nhau. Vậy B là một khẳng định đúng.
• EFGH là hình chữ nhật suy ra EF // GH.
Do đó EF và GH không cắt nhau. Vậy C là một khẳng định sai.
• ABCD là hình chữ nhật suy ra AD // BC.
Do đó AD và BC không cắt nhau. Vậy D là một khẳng định sai.
Câu 2. Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm,
AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Đáp án: A
Giải thích:
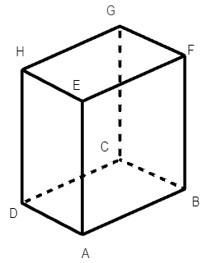
Từ hình hộp chữ nhật ABCD.EFGH ta có các mặt của hình hộp này đều là hình chữ nhật.
Khi đó ta có:
HG = DC = AB = 4 cm;
HE = DA = BC = 2 cm;
GC = HD = AE = 4 cm.
Vậy HG = 4 cm, HE = 2 cm, GC = 4 cm.
Câu 3. Hình lăng trụ đứng tứ giác có:
(1) Các mặt đáy song song với nhau;
(2) Các mặt đáy là tam giác;
(3) Các mặt đáy là tứ giác;
(4) Các mặt bên là hình chữ nhật.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
Hình lăng trụ đứng tứ giác có các mặt đáy là tứ giác và song song với nhau, các mặt bên là các hình chữ nhật.
Do đó (1) (3) (4) đúng.
Vậy có 3 khẳng định đúng.
Câu 4. Cho hình lăng trụ đứng ABCD.EHGF có đáy ABCD là hình thang cân (AB // CD). Có bao nhiêu cạnh có độ dài bằng với độ dài cạnh GH?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
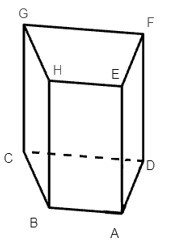
Do ABCD là hình thang cân nên ta có AD = BC (1)
Do ABCD.EHGF là hình lăng trụ đứng nên các mặt bên là hình chữ nhật.
• AEFD là hình chữ nhật nên AD = EF (2)
• BCGH là hình chữ nhật nên BC = GH (3)
Từ (1), (2) và (3) ta có AD = BC = EF = GH.
Vậy có 3 cạnh có độ dài bằng với cạnh GH.
Câu 5. Cho một hình lăng trụ đứng có tổng 12 cạnh. Hỏi đáy của hình lăng trụ đứng này không thể là hình gì?
A. Hình vuông;
B. Hình chữ nhật;
C. Hình tam giác;
D. Hình thoi.
Đáp án: D
Giải thích:
Hình lăng trụ đứng có 12 cạnh nên hình lăng trụ này là hình lăng trụ đứng tứ giác.
Do đó đáy của hình lăng trụ là một hình tứ giác, có thể là hình vuông hoặc hình chữ nhật, hình thoi.
Câu 5. Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước 4 cm, 9 cm. Chiều cao của lăng trụ đứng là 3 cm. Diện tích tất cả các mặt của hình lăng trụ đứng đó là:
A. 78 cm2;
B. 150 cm2;
C. 72 cm2;
D. 114 cm2.
Đáp án: B
Giải thích:
Diện tích xung quanh: 2.(4 + 9).3 = 78 (cm2).
Diện tích hai mặt đáy là: 2.4.9 = 72 (cm2).
Diện tích tất cả các mặt của hình lăng trụ đứng đó là:
78 + 72 = 150 (cm2).
Câu 6. Cho một hình khối như hình vẽ dưới đây:
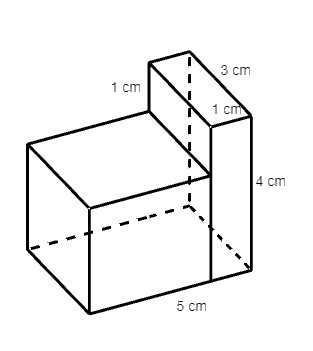
Thể tích hình khối trên là:
A. 46 cm3;
B. 47 cm3;
C. 48 cm3;
D. 49 cm3.
Đáp án: C
Giải thích:
Hình đã cho được tạo từ hai hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là 1 cm, 3 cm, 4 cm; hình hộp thứ hai có kích thước là 3 cm, 3 cm, 5 cm.
Thể tích hình hộp chữ nhật thứ nhất là: 1.3.4 = 12 (cm3).
Thể tích hình hộp chữ nhật thứ hai là: 3.3.4 = 36 (cm3).
Vậy thể tích của hình đã cho bằng: 12 + 36 = 48 (cm3).
Câu 7. Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A có chiều cao bằng 4 cm. Biết hai cạnh góc vuông của tam giác đáy bằng nhau và bằng một nửa cạnh bên của lăng trụ đó. Thể tích của lăng trụ bằng
A. 60 cm3;
B. 16 cm3;
C. 8 cm3;
D. 60 cm2.
Đáp án: C
Giải thích:
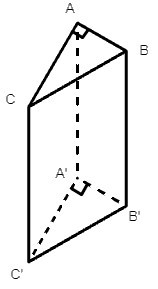
Theo bài ta có chiều cao của lăng trụ bằng 4 cm hay AA' = 4 (cm).
Khi đó ta có AB = AC = 4 : 2 = 2 (cm).
Vâỵ thể tích của lăng trụ đã cho là: .2.2.4 = 8 (cm3).
Câu 8. Cho hình lăng trụ đứng có diện tích xung quanh bằng 168 cm2, chiều cao 7 cm. Khi đó, chu vi đáy của hình lăng trụ đứng là:
A. 24 cm;
B. 12 cm;
C. 3 cm;
D. 4 cm.
Đáp án: A
Giải thích:
Chu vi đáy của hình lăng trụ đứng đó là:
C = Sxq : h = 168 : 7 = 24 (cm).
Vậy chu vi đáy của hình lăng trụ đó bằng 24 cm.
III. Vận dụng
Câu 1. Tấm bìa nào sau đây gấp được hình hộp lập phương?
A. 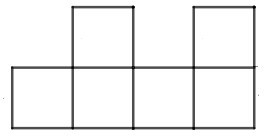
B. 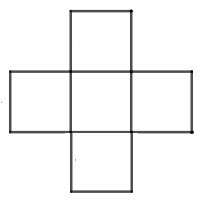
C. 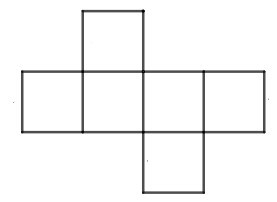
D. 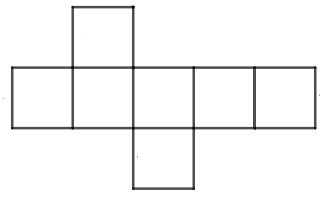
Đáp án: C
Giải thích:
Hình lập phương là hình có 6 mặt.
Quan sát các hình ở từng đáp án ta thấy:
Hình B có tất cả 5 mặt nên không gấp được hình lập phương có 6 mặt. Do đó B sai.
Hình D có tất cả 7 mặt nên không gấp được hình lập phương có 6 mặt. Do đó D sai.
Hình A có hai mặt đáy trên nhưng không có mặt đáy dưới nên A sai.
Câu 2. Phải gấp các cạnh nào của hình sau đây với nhau để được một hình lăng trụ đứng tứ giác? Cho biết chiều cao của tứ giác đó.
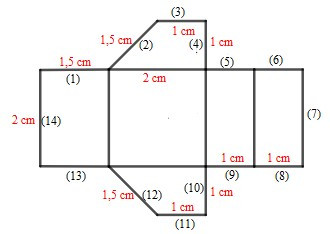
A. 4 và 5, 3 và 6, 2 và 1, 14 và 7, 12 và 13, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 2 cm;
B. 4 và 5, 3 và 6, 7 và 1, 14 và 2, 11 và 3, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 2 cm;
C. 4 và 5, 3 và 6, 7 và 1, 14 và 2, 11 và 13, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 1 cm;
D. 4 và 5, 3 và 6, 2 và 1, 14 và 7, 12 và 13, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 1 cm.
Đáp án: A
Giải thích:
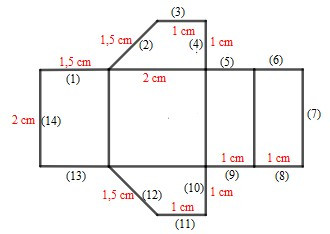
Ta phải gấp các cặp cạnh sau đây với nhau để hình trên trở thành một hình lăng trụ đứng tứ giác: 4 và 5, 3 và 6, 2 và 1, 14 và 7, 12 và 13, 11 và 8, 9 và 10.
Khi đó ta có hình sau:
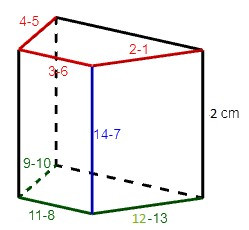
Ta có chiều cao của hình lăng trụ đứng này là: 2 cm.
Câu 3. Phương pháp đơn giản nhất để tạo một hình lăng trụ đứng tam giác từ hình sau là
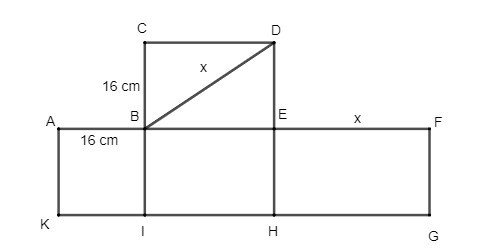
A. Cắt theo đoạn thẳng CE;
B. Cắt theo đoạn thẳng BD;
C. Cắt theo cạnh BE;
D. Cả A và B đều đúng.
Đáp án: A
Giải thích:
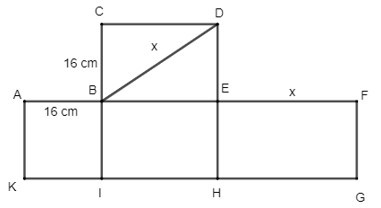
Phương pháp đơn giản nhất để tạo hình lăng trụ tam giác từ hình trên là:
Bước 1: Cắt theo cạnh CE khi đó ta có hình sau:
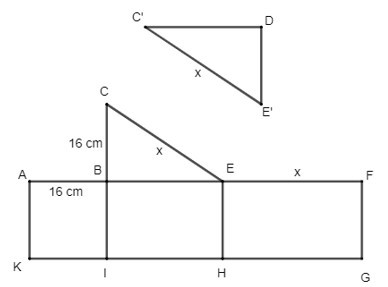
Bước 2: Ghép các cạnh sau với nhau: AK và FG; CB và AB; CE và EF, KI và DE'; DC' và IH; C'E' và HG.
Ta được hình lăng trụ đứng sau:
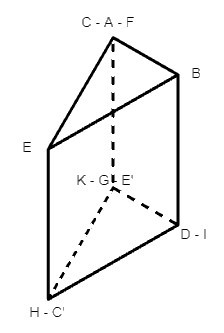
Vậy phương pháp đơn giản nhất để tạo một hình lăng trụ đứng tam giác từ hình đã cho là: Cắt theo đoạn thẳng CE.
Tương tự với cạnh BC.
Câu 4. Một chiếc tủ lạnh có hai ngăn (một ngăn mát và một ngăn đá) và thể tích ngăn đá bằng một nửa ngăn mát. Biết chiếc tủ lạnh này có dạng hình lăng trụ đứng cao 1,8 m với đáy là hình chữ nhật và có các kích thước 0,5 m, 0,7 m. Thể tích của ngăn mát là:
A. 0,21 m3;
B. 0,42 m3;
C. 0,63 m3;
D. 0,84 m3.
Đáp án: B
Giải thích:
Thể tích của chiếc tủ lạnh đứng này là:
1,8.0,5.0,7 = 0,63 (m3).
Gọi thể tích của ngăn mát là x (x > 0, m3).
Nên thể tích ngăn đá là (m3).
Khi đó ta có:
hay
(thỏa mãn).
Vậy thể tích của ngăn mát của tủ lạnh là 0,42 m3.
Câu 5. Một khối kim loại có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối kim loại dài 0,45 m (hình vẽ).
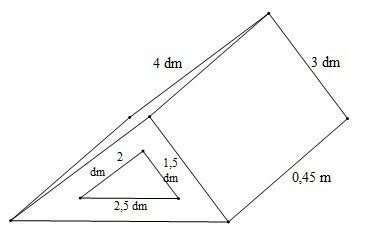
Người ta cần sơn toàn bộ các mặt của khối kim loại. Diện tích bề mặt phải sơn là:
A. 0,81 m2;
B. 0,765 m2;
C. 0,54 m2;
D. 0,495 m2.
Đáp án: B
Giải thích:
Đổi 3 dm = 30 cm; 4 dm = 40 cm; 5 dm = 50 cm;
1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm;
0,45 m = 45 cm.
Diện tích xung quanh của khối kim loại là:
(30 + 40 + 50).45 = 5 400 (cm2).
Diện tích xung quanh của cái lỗ là:
(20 + 15 + 25).45 = 2 700 (cm2).
Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:
.30.40 – .15.20 = 450 (cm2).
Diện tích bề mặt cần sơn là:
5 400 + 2 700 – 450 = 7 650 (cm2) = 0,765 (m2)
Các câu hỏi trắc nghiệm Toán lớp 7 sách Chân trời sáng tạo có đáp án, chọn lọc khác:
Trắc nghiệm Bài 1. Các góc ở vị trí đặc biệt
Trắc nghiệm Bài 2. Tia phân giác
Trắc nghiệm Bài 3. Hai đường thẳng song song
Xem thêm các chương trình khác:
