Nội dung bài viết

    Xem thêm

    TOP 15 câu Trắc nghiệm Toán lớp 7 (Chân trời sáng tạo 2024) có đáp án: Tập hợp các số hữu tỉ các số hữu tỉ có đáp án

    Bộ 15 bài tập trắc nghiệm Toán lớp 7 Bài 1. Tập hợp các số hữu tỉ các số hữu tỉ có đáp án đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 1.

    1 2,547 05/01/2024
    Mua tài liệu
    Trang trước
    Chia sẻ
    Trang sau  

    Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 7 Chân trời sáng tạo bản word (cả năm) có đáp án chi tiết:

    B1: Gửi phí vào tài khoản 033000255833 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank

    B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

    Xem thử tài liệu tại đây: Link tài liệu

    Trắc nghiệm Toán 7 Bài 1: Tập hợp các số hữu tỉ các số hữu tỉ - Chân trời sáng tạo

    I. Nhận biết

    Câu 1. Số nào dưới đây đang ở dạng phân số của số hữu tỉ?

    A. 20202021;

    B. 20,212022;

    C. 202120,22;

    D. 20220.

    Đáp án: A

    Giải thích:

    Số hữu tỉ là số viết được dưới dạng phân số ab, với a, b ∈ ℤ; b ≠ 0.

    Do đó ta sẽ đi tìm phân số có tử số, mẫu số đều là số nguyên và mẫu số khác 0.

    Trong tất cả các phương án chỉ có phân số 20202021 thỏa mãn điều kiện trên nên là số đang ở dạng phân số của số hữu tỉ.

    Câu 2. Tập hợp các số hữu tỉ được kí hiệu là:

    A. ℚ;

    B. ℤ;

    C. ℕ;

    D. ℝ.

    Đáp án: A

    Giải thích:

    Tập hợp các số hữu tỉ được kí hiệu là ℚ.

    Câu 3. Trong các số sau, số nào là số hữu tỉ dương?

    A. 2−3;

    B. −32;

    C. −−3−2;

    D. −3−2.

    Đáp án: D

    Giải thích:

    Số hữu tỉ dương là số hữu tỉ lớn hơn 0.

    Ta có: 2−3=−23<0; −32=−32<0; −−3−2=−32<0;−3−2=32>0.

    Do đó −3−2 là số hữu tỉ dương.

    Câu 4. Cho hai số hữu tỉ 3,5 và 5,25, trên trục số nằm ngang, điểm 3,5 ở:

    A. Bên phải điểm 5,25;

    B. Bên trái điểm 5,25;

    C. Trùng với điểm 5,25;

    D. Không có đáp án đúng.

    Đáp án: B

    Giải thích:

    Với hai số hữu tỉ bất kì x, y, nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

    Ta có 3,5 < 5,25 nên 3,5 nằm ở bên trái điểm 5,25.

    Câu 5. Chọn khẳng định sai:

    A. Số đối của số –3,5 là 3,5;

    B. Số đối của số –3,5 là 72;

    C. Số đối của số –3,5 là 72;

    D. Số đối của số –3,5 là 312

    Đáp án: C

    Giải thích:

    Số đối của số –3,5 là 3,5=72=312.

    Do đó phương án C sai.

    II. Thông hiểu

    Câu 1. Trong các phân số sau, phân số nào biểu diễn số hữu tỉ –0,5?

    A. 12;

    B. −12;

    C. 35;

    D. −35.

    Đáp án: B

    Giải thích:

    Ta có −0,5=−510=−12

    Vậy phân số biểu diễn số hữu tỉ –0,5 là −12.

    Câu 2. Chọn khẳng định đúng trong các khẳng định sau:

    A. Mỗi số hữu tỉ là một số nguyên;

    B. Số 0 là số hữu tỉ dương;

    C. Số hữu tỉ dương luôn lớn hơn số hữu tỉ âm;

    D. Cả A, B, C đều đúng.

    Đáp án: C

    Giải thích:

    • Xét phương án A: Mỗi số hữu tỉ là một số nguyên. Đây là khẳng định sai.

    Chẳng hạn, ta có số 3,5 là số hữu tỉ nhưng không phải là số nguyên nên A sai, D sai.

    • Xét phương án B: Số 0 là số hữu tỉ dương. Đây là khẳng định sai.

    Vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

    • Xét phương án C: Số hữu tỉ dương luôn lớn hơn số hữu tỉ âm. Đây là khẳng định đúng.

    Câu 3. Điền kí hiệu thích hợp vào chỗ trống: –2022,2023 … ℚ.

    A. ⸦;

    B. ∈;

    C. ∉;

    D. ∅.

    Đáp án: B

    Giải thích:

    Ta có: –2022,2023 … ℚ.

    Kí hiệu cần điền là kí hiệu dùng để so sánh phần tử với tập hợp.

    • Kí hiệu ⸦ dùng để so sánh hai tập hợp nên không sử dụng trong trường hợp này. Do đó A sai.

    • Kí hiệu ∅ là kí hiệu tập rỗng nên không sử dụng trong trường hợp này. Do đó D sai.

    • Vì –2022,2023 là số hữu tỉ nên ta sử dụng kí hiệu ∈.

    Vậy –2022,2022 ∈ ℚ.

    Câu 4. Điểm nào dưới đây biểu diễn số hữu tỉ −32?

    Tài liệu VietJack

    A. Điểm A;

    B. Điểm B;

    C. Điểm C;

    D. Điểm D.

    Đáp án: A

    Giải thích:

    • Điểm C biểu diễn số hữu tỉ 1 nên phương án C sai.

    • Ta có −32 là số hữu tỉ âm sẽ nằm bên trái điểm 0 nên điểm D nằm bên phải điểm 0 nên không thỏa mãn. Do đó phương án D sai;

    • Khoảng cách từ B đến O và khoảng cách từ C đến O là bằng nhau nên B biểu diễn điểm –1.

    Do đó điểm biểu diễn số hữu tỉ −32 là điểm A.

    Câu 5. Sắp xếp các số hữu tỉ sau theo thứ tự tứ nhỏ đến lớn: –2; 0; −35; 45.

    A. −35; 0; –2; 45;

    B. −35; –2; 0; 45;

    C. –2; −35; 0; 45;

    D. –2; −35; 45; 0.

    Đáp án: C

    Giải thích:

    • Ta có: −2=−105 và −35=−35.

    Vì –10 < –3 nên −105<−35

    Do đó –2 < −35

    • Mà số 0 luôn lớn hơn số hữu tỉ âm và luôn nhỏ hơn số hữu tỉ dương.

    Trong các số –2; 0; −35; 45 thì có các số hữu tỉ âm là –2; −35 và số hữu tỉ dương là 45

    Do đó −2<−35<0<45.

    Vậy các số được sắp xếp theo thứ tự từ nhỏ đến lớn là –2; 35; 0; 45.

    Câu 6. Số nào dưới đây không là số đối của số 1,5?

    A. 3−2;

    B. −112;

    C. −6−4;

    D. –1,5.

    Đáp án: C

    Giải thích:

    Ta có:

    • 3−2=−32=−1,5

    • −112=−32=−1,5

    • −6−4=32=1,5.

    Số 1,5 có số đối là số –1,5.

    Do đó phương án C có kết quả là số 1,5 không phải là số đối của số 1,5.

    Câu 7. Số 23 được biểu diễn trên trục số bởi hình vẽ nào dưới đây?

    A.

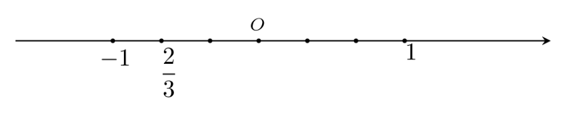
    Tài liệu VietJack

    B.

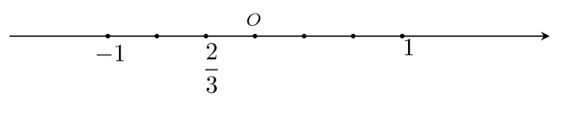
    Tài liệu VietJack

    C.

    Tài liệu VietJack

    D.

    Tài liệu VietJack

    Đáp án: A

    Giải thích:

    Biểu diễn số 23 trên trục số ta làm như sau:

    + Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 3 phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng 23 đơn vị cũ.

    + Số 23 được biểu diễn bởi điểm nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới.

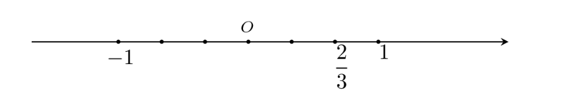
    Tài liệu VietJack

    III. Vận dụng

    Câu 1. Chiều cao (m) của các bạn trong tổ 1 được cho trong bảng sau:

    Tên

    An

    Bình

    Cường

    Dương

    Chiều cao

    1,5

    1,6

    1,54

    1,7

    Sắp xếp tên các bạn có chiều cao từ thấp đến cao ta được:

    A. An, Bình, Cường, Dương;

    B. An, Cường, Bình, Dương;

    C. Cường, An, Bình, Dương;

    D. Bình, An, Dương, Cường.

    Đáp án: B

    Giải thích:

    Chiều cao của An là 1,5 m.

    Chiều cao của Bình là 1,6 m.

    Chiều cao của Cường là 1,54 m.

    Chiều cao của Dương là 1,7 m.

    Ta có 1,5 < 1,54 < 1,6 < 1,7.

    Do đó sắp xếp tên theo chiều cao của các bạn (từ thấp đến cao) ta được: An, Cường, Bình, Dương.

    Câu 2. Trong cuộc thi tìm hiểu an toàn giao thông, bạn Nam đã trả lời đúng được 95% số câu trắc nghiệm, bạn Minh trả lời đúng được 28 câu trong số 30 câu trắc nghiệm. Khẳng định nào sau đây là đúng?

    A. Nam làm bài tốt hơn Minh;

    B. Minh làm bài tốt hơn Nam;

    C. Hai bạn trả lời số câu hỏi bằng nhau;

    D. Cả 3 khẳng định đều sai.

    Đáp án: A

    Giải thích:

    Ta có: 95%=95100=1920=5760 và 2830=5660

    Vì 57 > 56 nên 5760>5660

    Do đó 95% > 2830

    Vậy Nam làm bài tốt hơn Minh.

    Câu 3. Nhiệt độ nóng chảy của một số kim loại được cho trong bảng:

    Tên kim loại

    Sắt

    (Fe)

    Thuỷ ngân

    (Hg)

    Magie

    (Mg)

    Natri

    (Na)

    Wolfram

    (W)

    Nhiệt độ nóng chảy (℃)

    1538

    –38,83

    650

    97,72

    3410

    Hãy sắp xếp các kim loại trên theo nhiệt độ nóng chảy tăng dần.

    A. Na; Hg; Mg; Fe; W;

    B. Fe; Na; Hg; Mg; W;

    C. Hg; Mg; Fe; Na; W;

    D. Hg; Na; Mg; Fe; W.

    Đáp án: D

    Giải thích:

    Ta có –38,83 < 97,72 < 650 < 1538 < 3410

    Do đó các kim loại được sắp xếp theo nhiệt độ nóng chảy tăng dần là Hg; Na; Mg; Fe; W.

    Các câu hỏi trắc nghiệm Toán lớp 7 sách Chân trời sáng tạo có đáp án, chọn lọc khác:

    Trắc nghiệm Bài 2. Các phép tính với số hữu tỉ

    Trắc nghiệm Bài 3. Luỹ thừa của một số hữu tỉ

    Trắc nghiệm Bài 4. Quy tắc dấu ngoặc và quy tắc chuyển vế

    Trắc nghiệm Ôn tập chương 1

    Trắc nghiệm Bài 1. Số vô tỉ. Căn bậc hai số học

    Tham khảo các loạt bài Lớp 7 - Chân trời sáng tạo khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,547 05/01/2024
    Mua tài liệu
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: