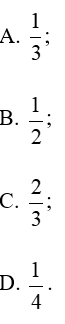TOP 15 câu Trắc nghiệm Tính chất ba đường trung tuyến của tam giác (Chân trời sáng tạo 2024) có đáp án - Toán 7
Bộ 15 câu hỏi trắc nghiệm Toán lớp 7 Bài 7: Tính chất ba đường trung tuyến của tam giác có đáp án đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 7.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 7 Chân trời sáng tạo bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 033000255833 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác - Chân trời sáng tạo
Câu 1. Điền vào chỗ trống sau: “Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua điểm ấy.”
Đáp án đúng là: C
Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua điểm ấy.
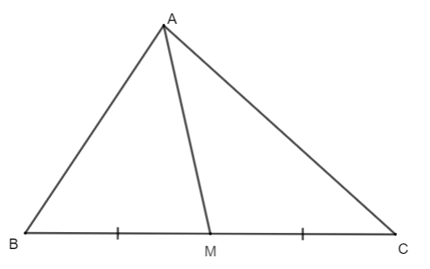
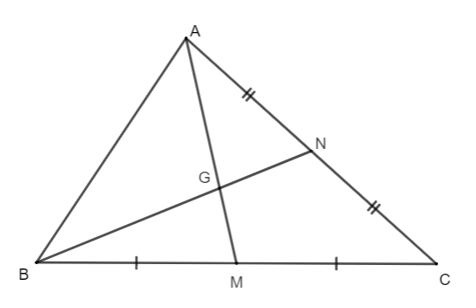
Câu 2. Cho hình như bên dưới. Đường thẳng AM trong hình bên dưới là:
A. Đường trung trực của tam giác ∆ABC;
B. Đường trung tuyến của tam giác ∆ABC;
C. Đường cao của tam giác ∆ABC;
D. Đường phân giác của tam giác ∆ABC.
Đáp án đúng là: B
Tam giác ∆ABC có AM là đường trung tuyến từ đỉnh A nối với trung điểm của M cạnh BC.
Câu 3. Giao điểm của ba đường trung trực của một tam giác:
A. Là trực tâm của tam giác đó;
B. Cách đều ba đỉnh của tam giác đó;
C. Là trọng tâm của tam giác đó;
D. Cách đều ba cạnh của tam giác đó.
Đáp án đúng là: C
Theo định nghĩa: Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm này được gọi là trọng tâm của tam giác.
Câu 4. Điền vào chỗ trống sau: “Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với ... của cạnh đối diện”.
A. Trung trực;
B. Trung điểm;
C. Trọng tâm;
D. Giao điểm.
Đáp án đúng là: B
Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.
Câu 5. Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
A.
B.
C.
D.
Đáp án đúng là: A
Xét ∆ABC có:
AM là đường trung tuyến (M là trung điểm của BC);
BN là đường trung tuyến (N là trung điểm của AC).
AM và BN cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Câu 6. Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
A.
B.
C.
D.
Đáp án đúng là: B
Xét ∆ABC có:
AM là đường trung tuyến (M là trung điểm của BC);
BN là đường trung tuyến (N là trung điểm của AC).
AM và BN cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra = (1)
Ta có: AG = AM − GM
Thay vào (1) ta được:
=
− =
1 − =
= 1− =
Vậy = .
Câu 7. Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng:
A.
B.
C.
D.
Đáp án đúng là: D
Xét ∆ABC có:
AM là đường trung tuyến (M là trung điểm của BC);
BN là đường trung tuyến (N là trung điểm của AC).
AM và BN cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra = và = .
Ta có: : = = : = .
Vậy = .
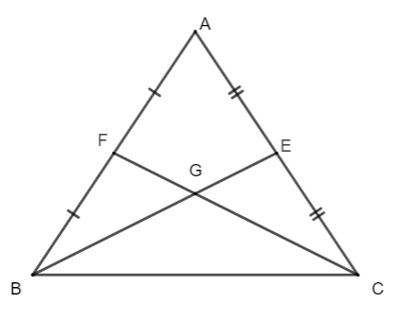
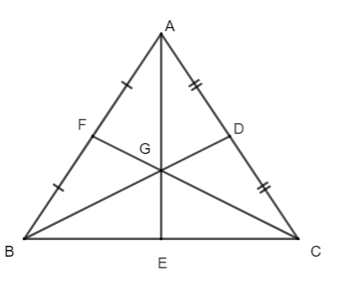
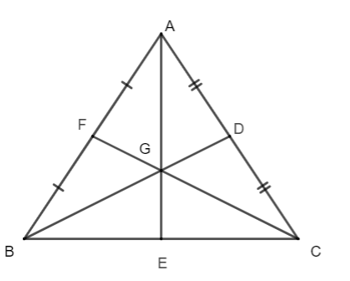
Câu 8. Cho tam giác ∆ABC cân tại A có hai điểm E và F lần lượt là trung điểm của AC và AB. Khi đó tam giác GBC là:
A. Tam giác cân;
B. Tam giác thường;
C. Tam giác đều;
D. Tam giác vuông.
Đáp án đúng là: A
Xét ∆ABC có:
BE là đường trung tuyến (E là trung điểm của AC);
CF là đường trung tuyến (F là trung điểm của AB);
BE và CF cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Ta có: ∆ABC cân tại A.
Suy ra AB = AC mà AB = 2AF; AC = 2AE
Do đó 2AF = 2AE hay AF = AE.
Xét ∆ABE và ∆ACF có:
là góc chung;
AB = AC(∆ABC cân tại A);
AE = AF (cmt).
Do đó ∆ABE = ∆ACF (c.g.c).
Suy ra CF = BE.
Mà CF = CG ; BE = BG (G là trọng tâm của ∆ABC).
Nên CG = BG hay CG = BG.
Vậy tam giác ∆GBC là tam giác cân.
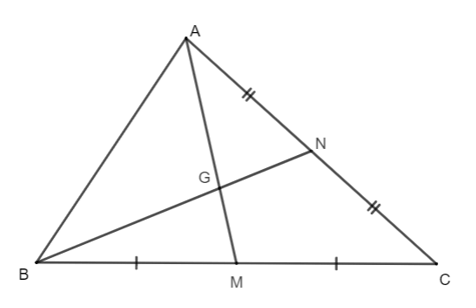
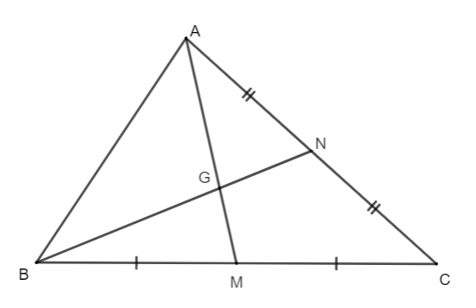
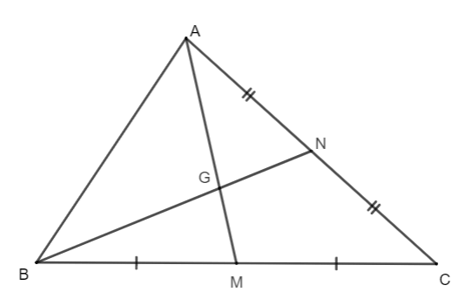
Câu 9. Cho hình vẽ như bên dưới. Biết AM = 12 cm. Tính chiều dài của đoạn thẳng AG.
A. 10 cm;
B. 4 cm;
C. 6 cm;
D. 8 cm.
Đáp án đúng là: D
Xét ∆ABC có:
AM là đường trung tuyến (M là trung điểm của BC);
BN là đường trung tuyến (N là trung điểm của AC).
AM và BN cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra =
=
AG = = = 8 (cm).
Vậy độ dài đoạn thẳng AG bằng 8 cm.
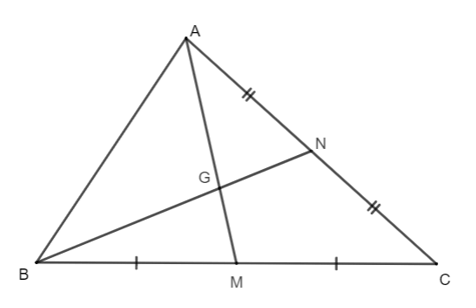
Câu 10. Cho hình vẽ như bên dưới. Biết GN = 4 cm. Độ dài đoạn thẳng BN bằng:
A. 12 cm;
B. 10 cm;
C. 14 cm;
D. 16 cm.
Đáp án đúng là: A
Xét ∆ABC có:
AM là đường trung tuyến (M là trung điểm của BC);
BN là đường trung tuyến (N là trung điểm của AC).
AM và BN cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra =
BN = 3GN = 3 . 4 = 12 (cm)
Vậy độ dài đoạn thẳng AG bằng 12 cm.
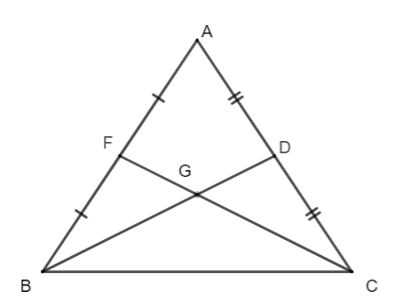
Câu 11. Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. Khi đó tam giác ∆ABC là:
A.Tam giác vuông;
B. Tam giác vuông cân;
C.Tam giác thường;
D.Tam giác cân.
Đáp án đúng là: D
Xét ∆ABC có:
BE là đường trung tuyến (E là trung điểm của AC);
CF là đường trung tuyến (F là trung điểm của AB);
BE và CF cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra = ; =
mà BD = CF (gt) nên BG = CG.
Do vậy FG = GD.
Xét ∆FGB và ∆DGC có:
BG = CG (cmt);
FG = GD (cmt);
( hai góc đối đỉnh).
Do đó ∆FGB = ∆DGC (c.g.c).
Suy ra BF = DC (hai cạnh tương ứng)
Ta có : AB = BF (F là trung điểm của AB);
AC= DC ( D là trung điểm của AC);
BF = DC (cmt).
Do đó AB = AC.
Vậy ∆ABC là tam giác cân tại A.
Câu 12. Cho ∆ABC có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = CF và AG cắt BC tại E. Số đo là :
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Đáp án đúng là: D
Xét ∆ABC có:
BE là đường trung tuyến (E là trung điểm của AC);
CF là đường trung tuyến (F là trung điểm của AB);
BE và CF cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra AE là đường trung tuyến của ∆ABC.
Do vậy E là trung điểm của BC.
Ta có: = ; = (G là trọng tâm ∆ABC)
mà BD = CF (gt) nên BG = CG.
Do vậy FG = GD.
Xét ∆FGB và ∆DGC có:
BG = CG (cmt);
FG = GD (cmt);
( hai góc đối đỉnh).
Do đó ∆FGB = ∆DGC (c.g.c).
Suy ra BF = DC (hai cạnh tương ứng).
Ta có : AB = BF (F là trung điểm của AB);
AC= DC (D là trung điểm của AC);
BF = DC (cmt).
Do đó AB = AC.
Xét ∆AEB và ∆AEC ta có:
AB = AC (cmt);
AE là cạnh chung;
EB = EC (E là trung điểm của BC).
Do đó ∆AEB = ∆AEC (c.c.c).
Suy ra = 90°.
Câu 13. Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = 9 cm. Độ dài đoạn thẳng GF bằng:
A. 6 cm;
B. 3 cm;
C. 4 cm;
D. 5 cm.
Đáp án đúng là: B
Xét ∆ABC có:
BE là đường trung tuyến (E là trung điểm của AC);
CF là đường trung tuyến (F là trung điểm của AB);
BE và CF cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Ta có: ∆ABC cân tại A.
Suy ra AB = AC mà AB = 2AF; AC = 2AD.
Do đó 2AF = 2AD hay AF = AD.
Xét ∆ABD và ∆ACF có:
là góc chung;
AB = AC(∆ABC cân tại A);
AD = AF (cmt).
Do đó ∆ABD = ∆ACF (c.g.c)
Suy ra BD = CF.
Ta có : GF= CF ;
BD = CF = 9 (cm).
Do đó GF = . 9 = 3 (cm).
Vậy độ dài đoạn thẳng GF bằng 3 cm.
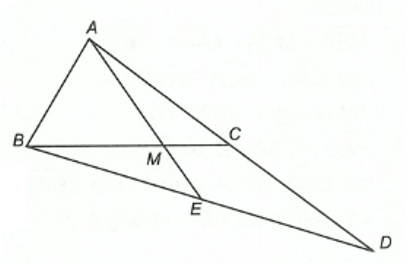
Câu 14. Cho tam giác ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là:
A. Trọng tâm của ΔABD;
B. Trọng tâm của ΔABC;
C. Trực tâm của ΔABC;
D. Cách đều ba đỉnh của ΔABD.
Đáp án đúng là: A
Xét ΔABD có AC = CD.
Do đó BC là trung tuyến của ΔABD.
Mà BM = 2MC nên BM = BC.
Suy ra M là trọng tâm của ΔABD.
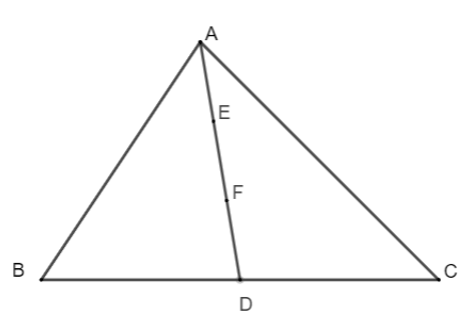
Câu 15. Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F sao cho AE = EF = FD. Điểm F là:
A. Trọng tâm của ΔABC;
B. Trực tâm của ΔABC;
C. Cách đều ba đỉnh của ΔABC;
D. Cách đều ba cạnh của ΔABC.
Đáp án đúng là: A
Ta có: AD = AE + EF + FD mà AE = EF = FD nên AD = 3AE.
Suy ra AE = EF = FD = AD.
Do đó AF = AD.
Vì AD là đường trung tuyến và AF = AD nên F là trọng tâm của ΔABC.
Xem thêm bài tập trắc nghiệm Toán lớp 7 Chân trời sáng tạo có đáp án hay khác:
Trắc nghiệm Toán 7 Bài 8: Tính chất ba đường cao của tam giác
Trắc nghiệm Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác
Trắc nghiệm Toán 7 Bài 1: Làm quen với biến cố ngẫu nhiên
Trắc nghiệm Toán 7 Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên
Xem thêm các chương trình khác: