Toán 7 Bài 2 (Chân trời sáng tạo): Số thực. Giá trị tuyệt đối của một số thực
Với giải bài tập Toán lớp 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 2.
Giải bài tập Toán 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực
Video giải bài tập Toán 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực
Hoạt động khởi động
Khởi động trang 35 Toán lớp 7 Tập 1: Người ta gọi tập hợp các số hữu tỉ và số vô tỉ là gì?
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Tập hợp gồm các số hữu tỉ và số vô tỉ là tập số thực.
1. Số thực và tập hợp các số thực
Khám phá 1 trang 35 Toán lớp 7 Tập 1: Trong các số sau, số nào là số hữu tỉ, số nào là số vô tỉ?
Lời giải:
Các số là số hữu tỉ là .
Các số là số vô tỉ là .
Lời giải:
a) là số vô tỉ nên do đó khẳng định sai.
Phát biểu đúng: hoặc hoặc
b) là số vô tỉ nên khẳng định đúng.
c) là số hữu tỉ nên khẳng định sai.
Phát biểu đúng: hoặc hoặc
d) –9 là số nguyên nên khẳng định đúng.
2. Thứ tự trong tập hợp các số thực
Khám phá 2 trang 35 Toán lớp 7 Tập 1: Hãy so sánh các số thập phân sau đây: 3,14; 3,1415; 3,141515.
Lời giải:
Ta có 3,14 = 3,140000; 3,1415 = 3,141500.
Do 3,140000 < 3,141500 < 3,141515 nên 3,14 < 3,1415 < 3,141515.
Vậy 3,14 < 3,1415 < 3,141515.
Thực hành 2 trang 36 Toán lớp 7 Tập 1: So sánh hai số thực:
Lời giải:
a) Ta có: 4,(56) = 4,565656…
Do 4,565656… > 4,56279 nên 4,(56) > 4,56279.
b) Ta có: –3,(65) = –3,6565…
Do 3,6565… > 3,6491 nên –3,6565… < –3,6491.
Vậy –3,(65) < –3,6491.
c) Ta có: 0,(21) = 0,212121…; 0,2(12) = 0,212121…
Do 0,212121… = 0,212121… nên 0,(21) = 0,2(12).
d) Ta có:
Do 1,414213562… < 1,42 nên
Lời giải:
Độ dài a của cạnh hình vuông bằng m.
Ta có:
Do 2,236067977… < 2,361 nên độ dài a của cạnh hình vuông nhỏ hơn độ dài b.
3. Trục số thực
Độ dài OA có là số hữu tỉ hay không?
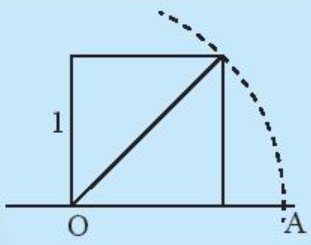
Lời giải:
Độ dài của đoạn thẳng OA bằng độ dài đường chéo trong hình vuông.
Hình vuông có cạnh bằng 1 thì độ dài đường chéo là
Do đó độ dài đoạn thẳng OA bằng
Số không phải số hữu tỉ nên độ dài đoạn thẳng OA không phải số hữu tỉ.
Thực hành 3 trang 36 Toán lớp 7 Tập 1: Hãy biểu diễn các số thực: –2; –1,5; 2; 3 trên trục số.
Lời giải:
Do –2 < 0; –1,5 < 0 và < 0 nên điểm –2, điểm và điểm –1,5 nằm ở bên trái điểm 0.
Do 2 > 0 và 3 > 0 nên điểm 2, điểm 3 nằm ở bên phải điểm 0.
+) Ta biểu diễn các điểm –2; 2; 3 như sau:
Do –2 < 0 nên điểm –2 nằm ở bên trái điểm 0 và cách điểm 0 một khoảng bằng 2 lần đoạn thẳng đơn vị.
Do 2 > 0 nên điểm 2 nằm ở bên phải điểm 0 và cách điểm 0 một khoảng bằng 2 lần đoạn thẳng đơn vị.
Do 3 > 0 nên điểm 3 nằm ở bên phải điểm 0 và cách điểm 0 một khoảng bằng 3 lần đoạn thẳng đơn vị.
+) Ta biểu diễn điểm như sau:
Ở bên trái điểm O, vẽ hình vuông có cạnh là 1, khi đó độ dài đường chéo bằng
Thực hiện vẽ cung tròn có tâm tại điểm 0, bán kính Cung tròn này cắt trục số tại điểm
+) Ta biểu diễn điểm –1,5 như sau:
Chia đoạn thẳng đơn vị thành 2 đoạn bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng đơn vị cũ.
Do –1,5 < 0 nên điểm –1,5 nằm ở bên trái điểm 0 và cách 0 một khoảng bằng 3 lần đơn vị mới.
Ta có hình vẽ như sau:
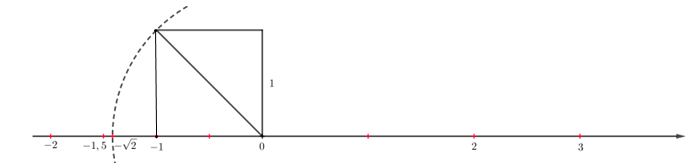
Lời giải:
Do và nên điểm nằm ở bên phải điểm 0.
Ta có ;
Do 1,414213562… < 1,5 nên
Do đó điểm nằm ở bên trái điểm
Vậy trên trục số, hai điểm và cùng nằm bên phải điểm 0, điểm ở bên trái điểm .
4. Số đối của một số thực
Khám phá 4 trang 37 Toán lớp 7 Tập 1:

Gọi A và A’ lần lượt là các điểm biểu diễn hai số 4,5 và –4,5 trên trục số. So sánh OA và OA’.
Lời giải:
Độ dài đoạn thẳng OA là 4,5 đơn vị.
Độ dài đoạn thẳng OA’ là 4,5 đơn vị.
Do đó, độ dài OA bằng với độ dài OA’.
Thực hành 4 trang 37 Toán lớp 7 Tập 1: Tìm số đối của các số thực sau: 5,12; .
Lời giải:
Số đối của số 5,12 là –5,12.
Số đối của số π là số .
Số đối của là
Vận dụng 3 trang 37 Toán lớp 7 Tập 1: So sánh các số đối của hai số và .
Lời giải:
Ta có:
Số đối của là .
Số đối của là .
Do nên
5. Giá trị tuyệt đối của một số thực
Khám phá 5 trang 37 Toán lớp 7 Tập 1: Trên trục số, so sánh khoảng cách từ điểm 0 đến hai điểm và .
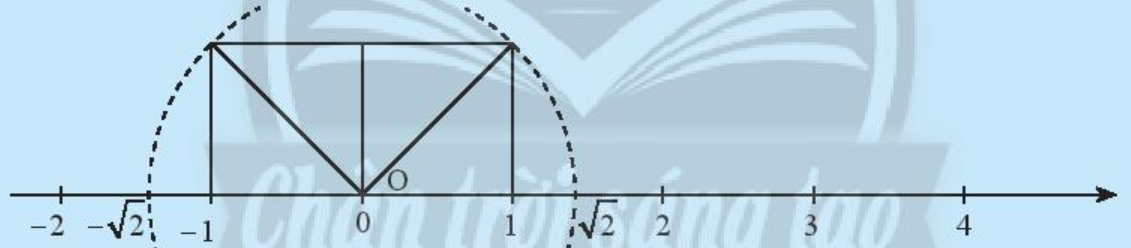
Lời giải:
Trên trục số, khoảng cách từ điểm 0 đến điểm bằng khoảng cách từ điểm 0 đến điểm
Lời giải:
Do –3,14 < 0 nên = –(–3,14) = 3,14.
Do 41 > 0 nên = 41.
Do –5 < 0 nên = –(–5) = 5.
Do 1,(2) > 0 nên
Do nên
Vận dụng 4 trang 37 Toán lớp 7 Tập 1: Có bao nhiêu số thực x thỏa mãn |x| =
Lời giải:
Nếu x < 0 thì = –x, khi đó –x = do đó
Nếu x > 0 thì = x, khi đó x =
Vậy có hai số thực x thỏa mãn
Bài tập
Bài 1 trang 38 Toán lớp 7 Tập 1: Hãy thay mỗi bằng kí hiệu ∈ hoặc ∉ để có phát biểu đúng.
Lời giải:
Bài 2 trang 38 Toán lớp 7 Tập 1: Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn:
Lời giải:
Ta có:
π = 3,141592654…;
Do 1,414213562… > 0,75 > 0,(6) > 0 nên –1,414213562… < –0,75 < –0,(6) < 0.
hay
Do 2,(3) < 3,141592654… < 3,2 < 4,1 nên 0 < < π < 3,2 < 4,1.
Do đó < π < 3,2 < 4,1.
Vậy các số theo thứ tự từ nhỏ đến lớn là: π; 3,2; 4,1.
Bài 3 trang 38 Toán lớp 7 Tập 1: Các khẳng định sau đúng hay sai?
b) Số nguyên không là số thực.
d) Số 0 vừa là số hữu tỉ vừa là số vô tỉ.
Lời giải:
a) Khẳng định “ là các số thực” là khẳng định đúng.
b) Khẳng định “Số nguyên không là số thực” là khẳng định sai.
c) Khẳng định “ –0,45 là các số thực” là khẳng định đúng.
d) Khẳng định “Số 0 vừa là số hữu tỉ vừa là số vô tỉ” là khẳng định sai.
e) Khẳng định “1; 2; 3; 4 là các số thực” là khẳng định đúng.
Bài 4 trang 38 Toán lớp 7 Tập 1: Hãy thay bằng các chữ số thích hợp.
Lời giải:
a) Để 2,71467 > thì 1 > do cặp chữ số hàng phần nghìn là 4 < 9.
Vậy ta điền số 0.
b) Ta có –5,17934 > nên 5,17934 <
Do cặp chữ số hàng phần trăm là 7 = 7 và cặp chữ số hàng phần chục nghìn là 3 < 4 nên . Mà chỉ có số 9 thỏa mãn điều này.
Vậy ta điền số 9.
Bài 5 trang 38 Toán lớp 7 Tập 1: Tìm số đối của các số sau: 12,(3); 0,4599; –π.
Lời giải:
Số đối của là
Số đối của 12,(3) là –12,(3).
Số đối của 0,4599 là –0,4599.
Số đối của là .
Số đối của –π là –(–π) = π.
Bài 6 trang 38 Toán lớp 7 Tập 1: Tìm giá trị tuyệt đối của các số sau: 52,(1); 0,68; 2π.
Lời giải:
Do < 0 nên
Do 52,(1) > 0 nên
Do 0,68 > 0 nên
Do nên
Do 2π > 0 nên
–3,2; 2,13;
Lời giải:
Do –3,2 < 0 nên = –(–3,2) = 3,2.
Do 2,13 > 0 nên = 2,13.
Do nên
Do nên
Ta có: = 1,414213562…; = 0,(428571);
Do 0,(428571) < 1,414213562… < 2,13 < 3,2 nên < < 2,13 < 3,2.
Vậy các số theo thứ tự từ nhỏ đến lớn theo giá trị tuyệt đối là:
Bài 8 trang 38 Toán lớp 7 Tập 1: Tìm giá trị của x và y biết rằng: |x| = và
Lời giải:
Xét
Nếu x > 0 thì = x, do đó x =
Nếu x < 0 thì = –x, do đó hay
Do = 0 nên y – 2 = 0 do đó y = 2.
Vậy x = hoặc và y = 2.
Bài 9 trang 38 Toán lớp 7 Tập 1: Tính giá trị của biểu thức: M =
Lời giải:
Do -9 < 0 nên = -(-9) = 9.
Do đó =
Vậy M = 3.
Lý thuyết Bài 2: Số thực. Giá trị tuyệt đối của một số thực-Cánh diều
1. Số thực và tập hợp các số thực
– Ta gọi chung số hữu tỉ và số vô tỉ là số thực.
– Tập hợp số thực được kí hiệu ℝ.
Cách viết x ∈ ℝ cho ta biết x là một số thực.
– Mỗi số thực chỉ có một trong hai dạng biểu diễn thập phân sau:
+ Dạng thập phân hữu hạn hay vô hạn tuần hoàn nếu số đó là số hữu tỉ.
+ Dạng thập phân vô hạn không tuần hoàn nếu số đó là số vô tỉ.
Ví dụ: Ta có các số 5; –3 ; 0,14 ; ; ; ; π ; ….là các số thực.
Ta viết 5 ∈ ℝ ; –3 ∈ ℝ ; 0,14 ∈ ℝ ; ∈ ℝ ; ∈ ℝ; ∈ ℝ ; π ∈ ℝ ; …
Chú ý: Trong các tập hợp đã học, tập hợp số thực là “rộng lớn” nhất bao gồm tất cả các số tự nhiên, số nguyên, số hữu tỉ và cả số vô tỉ.
– Trong tập hợp các số thực, ta cũng có các phép tính với các tính chất tương tự như các phép tính trong tập hợp các số hữu tỉ mà ta đã biết.
2. Thứ tự trong tập hợp các số thực
– Các số thập phân hữu hạn hoặc vô hạn đều có thể so sánh tương tự như so sánh hai số thập phân hữu hạn, đó là so sánh phần số nguyên, rồi đến phần thập phân thứ nhất, phần thập phân thứ hai, …
– Ta có thể so sánh hai số thực bằng cách so sánh hai số thập phân (hữu hạn hoặc vô hạn) biểu diễn chúng.
Do vậy: Với hai số thực x, y bất kì, ta luôn có hoặc x < y hoặc x > y hoặc x = y.
Chú ý: Với hai số thực dương a và b, ta có:
Nếu a > b thì .
Ví dụ: So sánh hai số thực:
a) 5,(56) và 5,566;
b) và 1,733;
c) –1,024 và –1,025;
d) và 3.
Hướng dẫn giải
a) Số 5,(56) = 5,565656… < 5,566 (do phần thập phân thứ ba của hai số ta thấy 5 < 6).
Vậy 5,(56) < 5,566.
b) Ta có: = 1,73205… < 1,733 (do phần thập phân thứ ba của hai số ta thấy 2 < 3).
Vậy < 1,733.
c) Ta có: 1,024 < 1,025 (do phần thập phân thứ ba của hai số ta thấy 4 < 5)
Suy ra: –1,024 > –1,025.
Vậy –1,024 > –1,025.
d) Do 8 < 9 nên ta có , tức là < 3 (vì = 3).
Vậy < 3.
3. Trục số thực
Ta đã biết một hình vuông có cạnh bằng 1 có độ dài đường chéo là
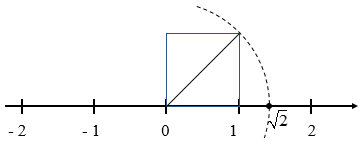
– Trên trục số ta biểu diễn được số vô tỉ . Vì vậy, không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ, nghĩa là các điểm biểu diễn số hữu tỉ không lấp đầy trục số.
Người ta chứng minh được rằng:
+ Mỗi số thực được biểu diễn bởi một điểm trên trục số
+ Ngược lại, mỗi điểm trên trục số biểu diễn một số thực.
Vì vậy, ta gọi trục số là trục số thực.
Chú ý:
– Điểm biểu diễn số thực x trên trục số được gọi là điểm x.
– Nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.
Ví dụ: Ta có: = 1,414213562… < 1,5.
Vậy điểm nằm bên trái điểm 1,5 trên trục số nằm ngang.
4. Số đối của một số thực
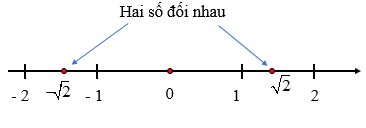
– Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này gọi là số đối của số kia.
– Số đối của số thực x kí hiệu là –x.
– Ta có x + (– x) = 0.
Ví dụ: Số đối của số là , số đối của là .
5. Giá trị tuyệt đối của một số thực
Giá trị tuyệt đối của một số thực x là khoảng cách từ điểm x đến điểm 0 trên trục số.
Giá trị tuyệt đối của một số thực x được kí hiệu là |x|.
Nhận xét: Ta có
Vậy giá trị tuyệt đối của một số thực x luôn là số không âm:
|x| ≥ 0 với mọi số thực x.
Ví dụ:
a)
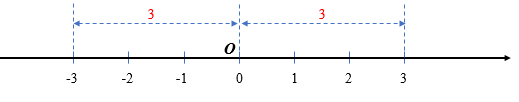
– Khoảng cách từ điểm –3 đến điểm 0 là 3 nên |–3| = 3.
– Khoảng cách từ điểm 3 đến gốc 0 là 3 nên |3| = 3.
b) Vì –2 < 0 nên |–2| = –(–2) = 2.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Số vô tỉ. Căn bậc hai số học
Bài 3: Làm tròn số và ước lượng kết quả
Bài 4: Hoạt động thực hành và trải nghiệm: Tính chỉ số đánh giá thể trạng BMI (Body mass index)
Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 2: Số thực. Giá trị tuyệt đối của một số thực
Trắc nghiệm Bài 2. Số thực. Giá trị tuyệt đối của một số thực
Xem thêm các chương trình khác:
- Soạn văn lớp 7 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Chân trời sáng tạo
- Soạn văn lớp 7 (ngắn nhất) – Chân trời sáng tạo
- Văn mẫu lớp 7 – Chân trời sáng tạo
- Giải sgk Lịch sử 7 – Chân trời sáng tạo
- Lý thuyết Lịch Sử 7 – Chân trời sáng tạo
- Giải sbt Lịch sử 7 – Chân trời sáng tạo
- Giải sgk Địa lí 7 – Chân trời sáng tạo
- Lý thuyết Địa Lí 7 – Chân trời sáng tạo
- Giải sbt Địa lí 7 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 7 Friend plus – Chân trời sáng tạo
- Giải sbt Tiếng Anh 7 Friend plus– Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 7 Friends plus đầy đủ nhất
- Bài tập Tiếng Anh 7 Friends plus theo Unit có đáp án
- Giải sgk Khoa học tự nhiên 7 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 7 – Chân trời sáng tạo
- Giải sbt Khoa học tự nhiên 7 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 7 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 7 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 7 – Chân trời sáng tạo
- Giải sgk Công nghệ 7 – Chân trời sáng tạo
- Lý thuyết Công nghệ 7 – Chân trời sáng tạo
- Giải sbt Công nghệ 7 – Chân trời sáng tạo
- Giải sgk Tin học 7 – Chân trời sáng tạo
- Lý thuyết Tin học 7 – Chân trời sáng tạo
- Giải sbt Tin học 7 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 7 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 7 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 7 – Chân trời sáng tạo
- Giải sgk Âm nhạc 7 – Chân trời sáng tạo
