Toán 7 Bài 2 (Chân trời sáng tạo): Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Giải bài tập Toán 7 Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Video giải bài tập Toán 7 Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Hoạt động khởi động

Giải Toán 7 trang 51 Tập 1

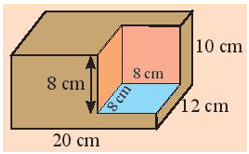
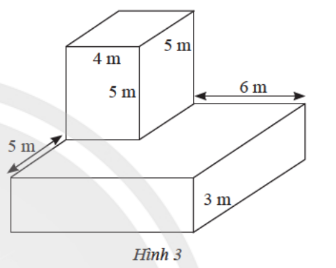
Khởi động trang 51 Toán lớp 7 Tập 1: Làm thế nào để tính được tổng diện tích các mặt và thể tích của khối gỗ ở hình bên?

Lời giải:

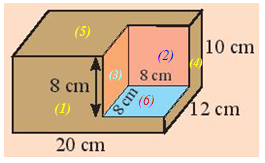
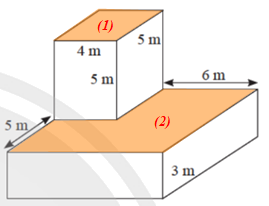
Ta đặt tên các mặt như hình vẽ dưới đây:

Diện tích những mặt trước của khối gỗ bằng diện tích mặt (1) cộng với diện tích mặt (2), bằng với diện tích mặt sau của khối gỗ.

Diện tích những mặt bên phải của khối gỗ bằng diện tích mặt (3) cộng với diện tích mặt (4), bằng với diện tích mặt bên trái của khối gỗ.

Diện tích những mặt trên của khối gỗ bằng diện tích mặt (5) cộng với diện tích mặt (6), bằng với diện tích mặt đáy dưới của khối gỗ.

Do đó, tổng diện tích của khối gỗ bằng diện tích xung quanh của khối gỗ có dạng hình hộp chữ nhật có các kích thước chiều dài 20 cm, chiều rộng 12 cm và chiều cao 10 cm.

Tổng diện tích các mặt của khối gỗ là:

2 . (20 + 12) . 10 = 640 (cm²).

Thể tích của khối gỗ bằng thể tích khối gỗ có dạng hình hộp chữ nhật (có ba kích thước 20 cm, 12 cm, 10 cm) trừ khi thể tích khối gỗ có dạng hình lập phương cạnh 8 cm.

Thể tích của khối gỗ có dạng hình hộp chữ nhật là:

20 . 12 . 10 = 2 400 (cm³).

Thể tích của khối gỗ lập phương có cạnh 8 cm là: 8³ = 512 (cm³).

Thể tích của khối gỗ trong hình là:

2 400 - 512 = 1 888 (cm³).

Vậy tổng diện tích các mặt và thể tích của khối gỗ lần lượt là 640 cm² và 1 888 cm³.

1. Nhắc lại công thức tính diện tích xung quanh và thể tích

2. Một số bài toán thực tế

Giải Toán 7 trang 52 Tập 1

Thực hành trang 52 Toán lớp 7 Tập 1: Một khối bê tông, được đặt trên mặt đất, có kích thước như Hình 3.

a) Người ta muốn sơn tất cả các mặt của khối bê tông trừ mặt tiếp giáp với mặt đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.

b) Tính thể tích của khối bê tông.

Lời giải:

a)

Hình hộp chữ nhật bên dưới có độ dài 2 cạnh lần lượt là 5 + 5 = 10 m và 4 + 6 = 10 m.

Diện tích xung quanh của hình hộp chữ nhật bên dưới là:

2 . (10 + 10) . 3 = 120 (m²).

Diện tích xung quanh của hình hộp chữ nhật bên trên là:

2 . (4 + 5) . 5 = 90 (m²).

Diện tích những mặt trên của khối bê tông bằng tổng diện tích của mặt (1) và mặt (2), bằng với diện tích mặt tiếp giáp với mặt đất của hình hộp chữ nhật bên dưới.

Diện tích mặt đáy của khối hình hộp chữ nhật bên dưới là: 10 . 10 = 100 (m²).

Diện tích muốn sơn bằng diện tích xung quanh của hai khối hình hộp cộng với diện tích đáy của hình hộp chữ nhật bên dưới (tổng diện tích của mặt (1) và mặt (2) trên hình vẽ).

Khi đó diện tích cần sơn là: 120 + 90 + 100 = 310 (m²).

Chi phí sơn là: 25 000 . 310 = 7 750 000 (đồng).

Vậy chi phí để sơn khối bê tông như Hình 3 là 7 750 000 đồng.

b) Thể tích của khối hình hộp chữ nhật bên dưới là: 10 . 10 . 3 = 300 (m³).

Thể tích của khối hình hộp bên trên là: 4 . 5 . 5 = 100 (m³).

Thể tích của khối bê tông là: 300 + 100 = 400 (m³).

Vậy thể tích của khối bê tông là 400 m³.

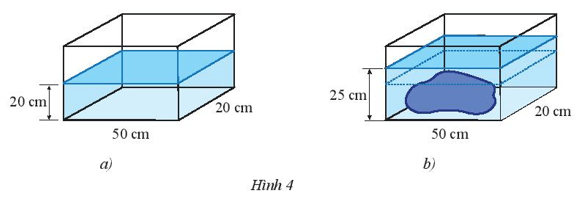
Vận dụng trang 52 Toán lớp 7 Tập 1: Để tính thể tích một hòn đá, bạn Na đã thực hiện như sau:

- Bạn ấy đổ nước vào cái bể kính hình hộp chữ nhật có hai cạnh đáy là 50 cm, 20 cm, mực nước đo được là 20 cm (Hình 4a).

- Sau đó bạn ấy đặt hòn đá vào bể thì thấy nước ngập hòn đá và mực nước đo được là 25 cm (Hình 4b).

Em hãy giúp bạn Na tính thể tích của hòn đá.

Lời giải:

Thể tích của nước trong bể kính khi chưa thả hòn đá là:

50 . 20 . 20 = 20 000 (cm³).

Thể tích của nước và hòn đá sau khi thả hòn đá là:

50 . 20 . 25 = 25 000 (cm³).

Thể tích của hòn đá là: 25 000 - 20 000 = 5 000 (cm³).

Vậy thể tích của hòn đá là: 5 000 cm³.

Bài tập

Giải Toán 7 trang 53 Tập 1

Bài 1 trang 53 Toán lớp 7 Tập 1: Hùng làm một con xúc xắc hình lập phương có kích thước như Hình 5a từ tấm bìa có hình dạng như Hình 5b. Em hãy tính diện tích tấm bìa và thể tích con xúc xắc.

Lời giải:

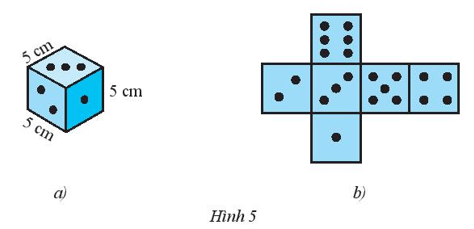
Diện tích tấm bìa bằng 6 lần diện tích một mặt bất kỳ có cạnh bằng 5 cm.

Diện tích một mặt bất kỳ bằng 5² = 25 (cm²).

Diện tích tấm bìa là: 6 . 25 = 150 (cm²).

Thể tích của con xúc xắc là: 5³ = 125 (cm³).

Vậy diện tích tấm bìa là 150 cm² và thể tích con xúc xắc là 125 cm³.

Bài 2 trang 53 Toán lớp 7 Tập 1: Hãy vẽ và gấp tấm bìa như Hình 6a thành một hình hộp chữ nhật như Hình 6b. Tính tổng diện tích các mặt và thể tích của hình hộp.

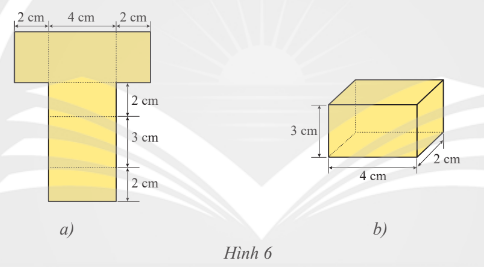
Lời giải:

Học sinh tự thực hiện việc vẽ và gấp hình.

Diện tích xung quanh của hình hộp là: 2 . (4 + 2) . 3 = 36 (cm²).

Diện tích hai đáy của hình hộp là: 2 . 2 . 4 = 16 (cm²).

Tổng diện tích các mặt của hình hộp là: 36 + 16 = 52 (cm²).

Thể tích của hình hộp là: 2 . 4 . 3 = 24 (cm³).

Vậy tổng diện tích các mặt của hình hộp là 52 cm², thể tích của hình hộp là 24 cm³.

Bài 3 trang 53 Toán lớp 7 Tập 1: Một chiếc bánh kem có dạng hình hộp chữ nhật với chiều dài 30 cm, chiều rộng 20 cm và chiều cao 15 cm. Người ta cắt đi một miếng bánh có dạng hình lập phương cạnh 5 cm. Tính thể tích phần còn lại của chiếc bánh kem.

Lời giải:

Thể tích của chiếc bánh kem ban đầu là: 30 . 20 . 15 = 9 000 (cm³)

Thể tích của miếng bánh cắt đi là: 5³ = 125 (cm³)

Thể tích phần còn lại của chiếc bánh kem là: 9 000 - 125 = 8 875 (cm³)

Vậy thể tích còn lại của chiếc bánh kem là 8 875 cm³.

Lý thuyết Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

1. Công thức tính diện tích xung quanh và thể tích

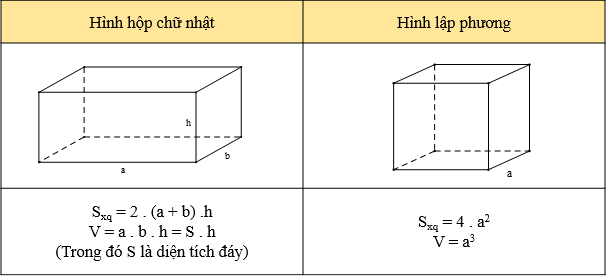
Ví dụ: Diện tích xung quanh và thể tích của hình lập phương có độ dài cạnh là 10 cm lần lượt là:

S_xq = 4 . a² = 4 . 10² = 400 (cm²);

V = a³ = 10³ = 1000 (cm³).

2. Một số bài toán thực tế

Ví dụ: Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình dưới. Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.

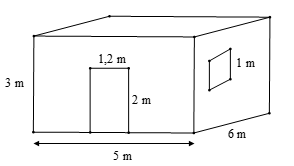
Hướng dẫn giải

Để tính được số tiền bác Long dùng để sơn căn phòng ta phải tính được diện tích phần cần sơn.

Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.

Diện tích xung quanh của căn phòng là:

S_xq = 2. (5 + 6) . 3 = 66 (m²).

Diện tích phần cửa lớn và cửa sổ là:

1,2 . 2 + 1 . 1 = 3,4 (m²)

Diện tích phần cần sơn là:

66 – 3,4 = 62,6 (m²).

Tổng chi phí cần để sơn là:

62,6. 30 000 = 1 878 000 (đồng).

Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.

Ví dụ: Bạn Ngọc muốn làm một hộp quà hình lập phương có kích thước cạnh là 30 cm bằng tấm bìa. Em hãy tính diện tích phần tấm bìa cần dùng và thể tích của hộp quà.

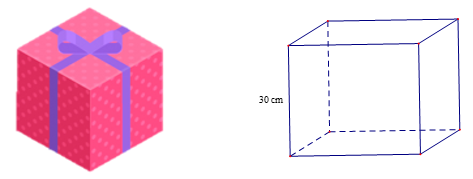
Hướng dẫn giải

Hộp quà hình lập phương nên ta có:

Diện tích tấm bìa cần dùng sẽ bằng diện tích xung quanh của hình lập phương cộng với diện tích hai mặt đáy.

Diện tích xung quanh của hộp quà là:

S_xq = 4 . 30² = 3 600 (cm²).

Diện tích đáy của hình lập phương là:

30 . 30 = 900 (cm²).

Vậy diện tích hai đáy của hình lập phương là:

2. 900 = 1 800 (cm²).

Diện tích tấm bìa cần dùng để làm hộp quà là:

3 600 + 1 800 = 5 400 (cm²).

Thể tích của hộp quà là

V = 30³ = 27 000 (cm³).

Vậy diện tích tấm bìa cần dùng là 5 400 cm² và thể tích của hộp quà là 27 000 cm³.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hình hộp chữ nhật - Hình lập phương

Bài 3: Hình lăng trụ đứng tam giác - Hình lăng trụ đứng tứ giác

Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

Bài 5: Hoạt động thực hành và trải nghiệm: Các bài toán về đo đạc và gấp hình

Bài tập cuối chương 3

Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Trắc nghiệm Bài 2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương