Giải Toán 7 Bài 4 (Chân trời sáng tạo): Đường vuông góc và đường xiên

Giải bài tập Toán 7 Bài 4: Đường vuông góc và đường xiên 

A. Các câu hỏi trong bài

Giải Toán 7 trang 64 Tập 2

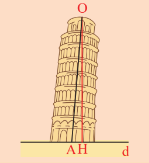
Khởi động trang 64 Toán 7 Tập 2:

Dây dọi OH hay trục của tháp nghiêng OA vuông góc với đường thẳng d (biểu diễn mặt đất)?

 

Lời giải:

Đặt thước êke sao cho đường thẳng d trùng với một cạnh góc vuông của thước.

Ta kiểm tra thấy cạnh OH trùng với cạnh góc vuông còn lại của thước.

Do đó dây dọi OH vuông góc với đường thẳng d.

Khám phá 1 trang 64 Toán 7 Tập 2:

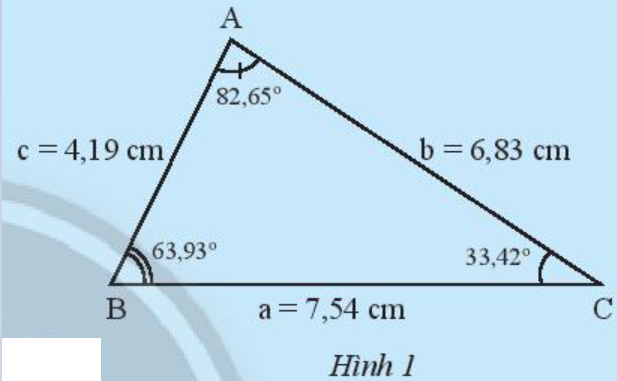
Cho tam giác ABC trong Hình 1.

 

- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a, b, c.

- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn của ba góc A, B, C là các góc đối diện với ba cạnh a, b, c.

- Nêu nhận xét của em về hai kết quả sắp xếp trên.

Lời giải:

• Ta có: 4,19 cm < 6,83 cm < 7,54 cm nên c < b < a.

Do đó, độ dài ba cạnh của tam giác theo thứ tự từ nhỏ đến lớn: c, b, a.

• Ta có: 33,42^o < 63,93^o < 82,65^o nên $\widehat{C}<\widehat{B}<\widehat{A}$.

Do đó, độ lớn các góc A, B, C theo thứ tự từ nhỏ đến lớn: góc C, góc B, góc A.

• Nhận xét: Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn và ngược lại, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Thực hành 1 trang 64 Toán 7 Tập 2:

 

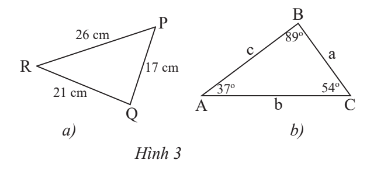
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR trong Hình 3a.

b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC trong Hình 3b.

Lời giải:

a) Ta có 17 cm < 21 cm < 26 cm hay PQ < RQ < RP.

Suy ra $\widehat{R}<\widehat{P}<\widehat{Q}$.

Do đó, số đo các góc được sắp xếp theo thứ tự từ nhỏ đến lớn là: $\widehat{R};\widehat{P};\widehat{Q}$.

b) Ta có 37^o < 54^o < 89^o hay $\widehat{A}<\widehat{C}<\widehat{B}$.

Suy ra BC < AB < AC.

Do đó, độ dài các cạnh được sắp xếp theo thứ tự từ nhỏ đến lớn là: BC; AB; AC.

Vận dụng 1 trang 64 Toán 7 Tập 2:

a) Cho tam giác DEF có góc F là góc tù. Cạnh nào cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF?

b) Cho tam giác ABC vuông tại A. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC?

Lời giải:

a)

 

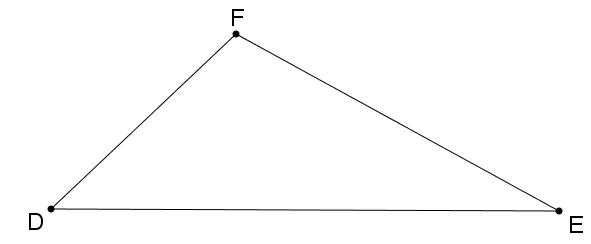
Vì ∆DEF có góc F là góc tù nên góc F là góc lớn nhất trong tam giác.

Khi đó, cạnh đối diện với góc F là cạnh có độ dài lớn nhất trong tam giác.

Cạnh đối diện với góc F trong ∆DEF là cạnh DE.

Vậy DE là cạnh có độ dài lớn nhất của ∆DEF.

b)

 

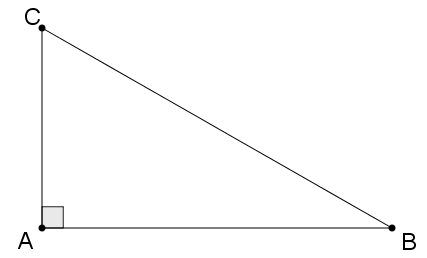
Vì ∆ABC vuông tại A nên góc A là góc vuông.

Do đó, góc A là góc lớn nhất trong tam giác.

Khi đó, cạnh đối diện với góc A là cạnh có độ dài lớn nhất trong tam giác.

Cạnh đối diện với góc A trong ∆ABC là cạnh BC.

Vậy BC là cạnh có độ dài lớn nhất của ∆ABC.

Giải Toán 7 trang 65 Tập 2

Khám phá 2 trang 65 Toán 7 Tập 2:

Trong hình xe cần cẩu ở Hình 4, ta có đoạn thẳng MA biểu diễn trục cần cẩu, đoạn thẳng MH biểu diễn sợi cáp kéo dài (từ đỉnh tay cẩu đến mặt đất), đường thẳng d biểu diễn mặt đất. Theo em, trong hai đoạn thẳng MA và MH, đoạn nào vuông góc với đường thẳng d?

 

Lời giải:

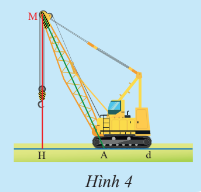
Kiểm tra tính vuông góc của đoạn thẳng MA và MH với đường thẳng d:

Đặt thước êke sao cho đường thẳng d trùng với một cạnh góc vuông của thước và điểm M trùng với đỉnh của góc vuông của thước êke.

Khi đó, ta thấy đoạn MH trùng với cạnh góc vuông còn lại của thước; đoạn MA không trùng với cạnh góc vuông còn lại của thước..

Do đó, đoạn thẳng MH vuông góc với đường thẳng d.

Vậy đoạn MH vuông góc với đường thẳng d.

Khám phá 3 trang 65 Toán 7 Tập 2:

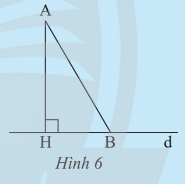
Quan sát tam giác vuông AHB ở Hình 6.

 

a) Hãy cho biết trong hai góc AHB và ABH, góc nào lớn hơn.

b) Từ câu a, hãy giải thích vì sao AB > AH.

Lời giải:

a) ∆AHB vuông tại H nên $\widehat{AHB}=90°$.

Suy ra góc H là góc lớn nhất trong tam giác.

Do đó $\widehat{AHB}>\widehat{ABH}$.

b) ∆AHB có $\widehat{AHB}>\widehat{ABH}$.

Suy ra cạnh đối diện với $\widehat{AHB}$ có độ dài lớn hơn cạnh đối diện với $\widehat{ABH}$.

Mà cạnh đối diện với $\widehat{AHB}$ và $\widehat{ABH}$ lần lượt là AB và AH.

Do đó AB > AH.

Thực hành 2 trang 65 Toán 7 Tập 2:

Trong Hình 8, tìm đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BF. Trong số các đường này, đường nào ngắn nhất?

 

Lời giải:

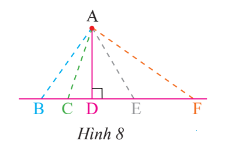
Đường vuông góc kẻ từ A đến đường thẳng BF là đoạn thẳng AD.

Đường xiên kẻ từ A đến đường thẳng BF là các đoạn thẳng AB, AC, AE, AF.

Khi đó, AD là đường ngắn nhất trong các đường AB, AC, AD, AE, AF.

Giải Toán 7 trang 66 Tập 2

Vận dụng 2 trang 66 Toán 7 Tập 2:

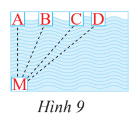
Bạn Minh xuất phát từ điểm M bên hồ bơi (Hình 9).

 

Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Minh phải bơi theo đường nào?

Lời giải:

Trong Hình 9:

• Đường vuông góc từ M đến AD là đoạn thẳng MA.

• Các đường xiên từ M đến AD là đoạn thẳng MB, MC, MD.

Khi đó MA có độ dài ngắn nhất.

Vậy đường ngắn nhất để bơi đến thành hồ đối diện thì Minh phải bơi theo đường MA.

B. Bài tập

Bài 1 trang 66 Toán 7 Tập 2:

a) So sánh các góc của tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 6 cm.

b) So sánh các cạnh của tam giác ABC có $\widehat{A}=50°$, $\widehat{C}=50°$.

Lời giải:

a) Ta có 7 cm > 6 cm > 4 cm hay BC > AC > AB.

Do đó $\widehat{A}>\widehat{B}>\widehat{C}$.

b) Xét ∆ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng số đo ba góc của một tam giác)

Suy ra $\widehat{B}=180°-\widehat{A}-\widehat{C}$

Do đó $\widehat{B}=180°-50°-50°=80°$.

Khi đó $\widehat{B}>\widehat{A}=\widehat{C}$.

Suy ra AC > BC = AB.

Vậy AC > BC = AB.

Bài 2 trang 66 Toán 7 Tập 2:

Cho tam giác ABC có $\widehat{A}=100°$, $\widehat{B}=40°$.

a) Tìm cạnh lớn nhất của tam giác ABC.

b) Tam giác ABC là tam giác gì? Vì sao?

Lời giải:

a) Tam giác ABC có $\widehat{A}=100°>90°$ nên $\widehat{A}$ là góc tù.

Do $\widehat{A}$ là góc tù nên $\widehat{A}$ là góc lớn nhất trong tam giác ABC.

Khi đó cạnh BC đối diện với $\widehat{A}$ là cạnh lớn nhất trong tam giác ABC.

Vậy BC là cạnh lớn nhất trong tam giác ABC.

b) Xét $∆$ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng số đo ba góc của một tam giác)

Suy ra $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-100°-40°=40°$.

Tam giác ABC có $\widehat{B}=\widehat{C}=40°$ nên tam giác ABC cân tại A.

Bài 3 trang 66 Toán 7 Tập 2:

Cho tam giác ABC vuông tại A có $\widehat{B}>45°$.

a) So sánh các cạnh của tam giác ABC.

b) Lấy điểm K bất kì thuộc đoạn thẳng AC. So sánh độ dài BK và BC.

Lời giải:

 

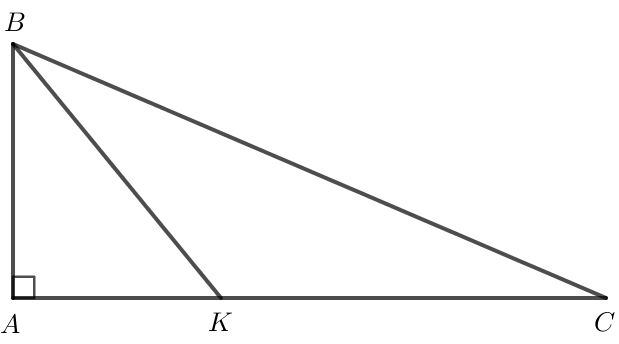
a) Xét ∆ABC vuông tại A nên $\widehat{B}+\widehat{C}=90°$và $\widehat{A}=90°$.

Suy ra $\widehat{A}$ là góc lớn nhất trong ∆ABC (1)

Vì $\widehat{B}>45°=\frac{90°}{2}$ nên $\widehat{C}<45°$ hay $\widehat{B}>\widehat{C}$ (2).

Từ (1) và (2) suy ra: $\widehat{A}>\widehat{B}>\widehat{C}$.

Do đó BC > CA > AB.

b) Ta có $\widehat{BKC}+\widehat{BK\text{A}}=180°$ (hai góc kề bù).

Suy ra $\widehat{BKC}=180°-\widehat{BK\text{A}}$ (3)

Xét ∆ABK có $\widehat{BK\text{A}}+\widehat{BAK}+\widehat{ABK}=180°$ (tổng số đo ba góc của một tam giác).

Suy ra $\widehat{BAK}+\widehat{ABK}=180°-\widehat{BK\text{A}}$ (4)

Từ (3) và (4) ta có $\widehat{BKC}=\widehat{BAK}+\widehat{ABK}=90°+\widehat{ABK}>90°$.

Khi đó $\widehat{BKC}$ là góc tù.

Vì ∆BKC có $\widehat{BKC}$ là góc tù nên $\widehat{BKC}$ là góc lớn nhất trong ∆BKC.

Do đó cạnh BC đối diện với góc BKC là cạnh lớn nhất trong ∆BKC.

Vậy BK < BC.

Bài 4 trang 66 Toán 7 Tập 2:

Quan sát Hình 10.

 

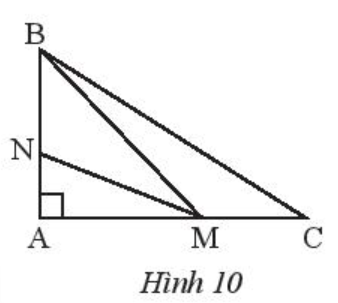
a) Tìm đoạn ngắn nhất trong các đoạn BA, BM, BC.

b) Tìm đoạn ngắn nhất trong các đoạn MA, MN, MB.

c) Chứng minh rằng MA < BC.

Lời giải:

a) Trong Hình 10:

• Đường vuông góc kẻ từ B đến AC là BA.

• Các đường xiên kẻ từ B đến AC là BM và BC.

Do đó BA là đoạn ngắn nhất trong các đoạn BA, BM, BC.

b) Trong Hình 10:

• Đường vuông góc kẻ từ M đến AB là MA.

• Các đường xiên kẻ từ M đến AB là MN và MB.

Do đó MA là đoạn ngắn nhất trong các đoạn MA, MN, MB.

c) • $\widehat{BMC}+\widehat{BMA}=180°$ (hai góc kề bù)

Suy ra $\widehat{BMC}=180°-\widehat{BMA}$.

• $\widehat{BMA}+\widehat{BAM}+\widehat{ABM}=180°$ (tổng ba góc trong ∆ABM).

Suy ra $\widehat{BAM}+\widehat{ABM}=180°-\widehat{BMA}$.

Do đó $\widehat{BMC}=\widehat{BAM}+\widehat{ABM}=90°+\widehat{ABM}>90°$.

Khi đó $\widehat{BMC}$ là góc tù.

Tam giác BMC có $\widehat{BMC}$ là góc tù nên $\widehat{BMC}$ là góc lớn nhất trong ∆BMC.

Suy ra cạnh BC đối diện với góc BMC là cạnh lớn nhất trong ∆BMC.

Hay BM < BC.

Mặt khác, theo câu a ta có MA < MB.

Suy ra MA < MB < BC.

Vậy MA < BC.

Bài 5 trang 66 Toán 7 Tập 2:

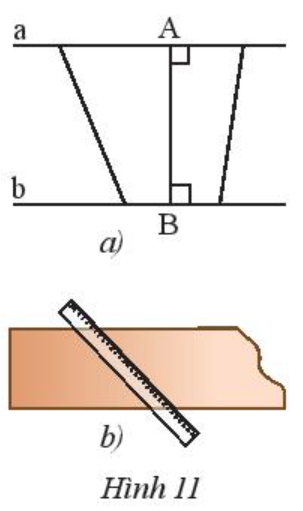
Trong Hình 11a, ta gọi độ dài đoạn thẳng AB là khoảng cách giữa hai đường thẳng song song a và b.

 

a) Một thanh nẹp gỗ có hai cạnh song song (Hình 11b). Chiều rộng của thanh nẹp gỗ là khoảng cách giữa hai cạnh đó.

Hãy cho biết có phải chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điểm trên cạnh kia không.

b) Muốn đo chiều rộng của thanh nẹp, ta phải đặt thước như thế nào? Tại sao?

Lời giải:

a) Chiều rộng của thanh nẹp gỗ là khoảng cách giữa hai cạnh của thanh nẹp gỗ nên chiều rộng của thanh nẹp gỗ là đoạn thẳng vuông góc với hai cạnh đó.

Mà khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điểm trên cạnh kia chính là độ dài đoạn thẳng vuông góc với cả hai cạnh đó.

Vậy chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điểm trên cạnh kia.

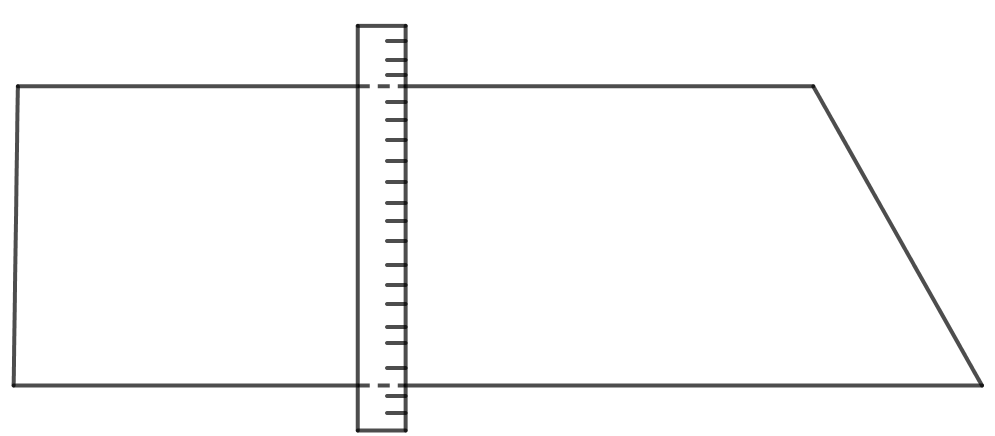
b) Vì chiều rộng của thanh nẹp gỗ là độ dài đoạn thẳng vuông góc với hai cạnh của thanh nẹp gỗ nên ta cần đặt thước sao cho thước vuông góc với hai cạnh của thanh nẹp.

Ta có hình vẽ sau:

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 3: Tam giác cân

Bài 4: Đường vuông góc và đường xiên

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 7: Tính chất ba đường trung tuyến của tam giác

•