Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 2

Giải bài tập Toán 7 Bài tập cuối chương 2

Video giải bài tập Toán 7 Bài tập cuối chương 2

Bài tập

Giải Toán 7 trang 45 Tập 1

Bài 1 trang 45 Toán lớp 7 Tập 1: Viết các phân số sau dưới dạng số thập phân:

a) $\frac{5}{16};$ $-\frac{7}{50};$ $\frac{11}{40};$ $\frac{9}{200}.$

b) $\frac{1}{7};$ $\frac{1}{11};$ $\frac{3}{13};$ $-\frac{5}{12}.$

Lời giải:

Thực hiện phép chia ta thu được:

a) $\frac{5}{16}$ = 0,3125; $-\frac{7}{50}$ = -0,14; $\frac{11}{40}$ = 0,275; $\frac{9}{200}$ = 0,045.

b) $\frac{1}{7}$ = 0,(142857); $\frac{1}{11}$ = 0,(09); $\frac{3}{13}$ = 0,(230769); $-\frac{5}{12}$ = -0,41(6).

Bài 2 trang 45 Toán lớp 7 Tập 1: Hai số 3,4(24) và 3,(42) có bằng nhau không?

Lời giải:

Ta có: 3,4(24) = 3,4242424… và 3,(42) = 3,424242…

Do 3,4242424… = 3,424242… nên 3,4(24) = 3,(42).

Vậy 3,4(24) = 3,(42).

Bài 3 trang 45 Toán lớp 7 Tập 1: Tính:

$\sqrt{91};\sqrt{49};\sqrt{{12}^2};\sqrt{{\left(-4\right)}^2}$.

Lời giải:

Ta có: $\sqrt{91}=9,539392014\dots \approx 9,54;$

$\sqrt{49}=\sqrt{7^2}=7;$ $\sqrt{{12}^2}=12;$

$\sqrt{{\left(-4\right)}^2}=\sqrt{16}=\sqrt{4^2}=4.$

Bài 4 trang 45 Toán lớp 7 Tập 1: Các phát biểu sau đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng.

a) $\sqrt{9}\in \mathbb{Q}$;

b) $\sqrt{5}\in ℝ$;

c) $\frac{11}{9}\notin ℝ$;

d) $-\sqrt{7}\in ℝ$.

Lời giải:

a) Ta có $\sqrt{9}$ = 3; $3=\frac{3}{1};$

Mà 3; 1 $\in \mathbb{Z};$ và $1\ne 0$ nên $3\in \mathbb{Q}.$

Do đó phát biểu $\sqrt{9}\in \mathbb{Q}$ là phát biểu đúng.

b) Phát biểu $\sqrt{5}\in ℝ$ là phát biểu đúng.

c) Ta có $11;9\in \mathbb{Z}$ và $9\ne 0$ nên $\frac{11}{9}\in \mathbb{Q}.$ Khi đó $\frac{11}{9}\in ℝ.$

Do đó phát biểu $\frac{11}{9}\notin ℝ$ là phát biểu sai.

Sửa lại: $\frac{11}{9}\in ℝ$ hoặc $\frac{11}{9}\in \mathbb{Q}$ hoặc $\frac{11}{9}\notin \mathrm{𝕀}.$

d) Phát biểu $-\sqrt{7}\in ℝ$ là phát biểu đúng.

Bài 5 trang 45 Toán lớp 7 Tập 1: Tìm x, biết: ${\left(x-5\right)}^2=64$.

Lời giải:

(x – 5)² = 64

(x – 5)² = 8² = (–8)²

x – 5 = 8 hoặc x – 5 = –8

x = 8 + 5 hoặc x = –8 + 5

x = 13 hoặc x = –3

Vậy x = 13; x = –3.

Bài 6 trang 45 Toán lớp 7 Tập 1: Dân số của Thành phố Hồ Chí Minh tính đến tháng 1 năm 2021 là 8 993 083 người (nguồn https://top10tphcm.com).

Hãy làm tròn số trên đến hàng nghìn.

Lời giải:

Gạch chân dưới chữ số hàng nghìn của số 8 993 083 được 8 993 083.

Chữ số liền kề bên phải của chữ số 3 vừa gạch chân là chữ số 0 < 5 nên giữ nguyên chữ số vừa gạch chân và thay các chữ số phía sau bằng các chữ số 0.

Khi đó ta được số 8 993 000.

Vậy dân số của Thành phố Hồ Chí Minh tính đến tháng 1 năm 2021 xấp xỉ 8 993 000 người.

Bài 7 trang 45 Toán lớp 7 Tập 1: Làm tròn đến hàng phần mười giá trị của biểu thức: A = $\frac{54,11.6,95}{26,15}$ theo hai cách sau:

Cách 1: Làm tròn mỗi số trước khi thực hiện phép tính.

Cách 2: Thực hiện phép tính trước rồi làm tròn kết quả nhận được.

Lời giải:

Cách 1:

+) Làm tròn số 54,11:

Gạch chân dưới chữ số hàng phần mười của số 54,11 được 54,11.

Chữ số liền kề bên phải của chữ số 1 vừa gạch chân là chữ số 1 < 5 nên giữ nguyên chữ số vừa gạch chân và bỏ đi các chữ số phía sau.

Khi đó 54,11 ≈ 54,1.

+) Làm tròn số 6,95:

Gạch chân dưới chữ số hàng phần mười của số 6,95 được 6,95.

Chữ số liền kề bên phải của chữ số 9 vừa gạch chân là chữ số 5 nên thực hiện cộng thêm 1 vào chữ số vừa gạch chân và bỏ đi các chữ số phía sau.

Khi đó ta được 10 nên thực hiện cộng 1 vào chữ số hàng đơn vị và bỏ đi phần thập phân.

Do đó 6,95 ≈ 7.

+) Làm tròn số 26,15:

Gạch chân dưới chữ số hàng phần mười của số 26,15 được 26,15.

Chữ số liền kề bên phải của chữ số 1 vừa gạch chân là chữ số 5 nên thực hiện cộng thêm 1 vào chữ số vừa gạch chân và bỏ đi các chữ số phía sau.

Khi đó 26,15 ≈ 26,2.

Thực hiện phép tính A $\approx$ $\frac{54,1.7}{26,2}=\frac{378,7}{26,2}$ = 14,45419847…

Gạch chân dưới chữ số hàng phần mười của A được 14,45419847…

Chữ số liền kề bên phải của chữ số 4 vừa gạch chân là chữ số 5 nên thực hiện cộng thêm 1 vào chữ số vừa gạch chân và bỏ đi các chữ số phía sau.

Khi đó ta được số 14,5.

Vậy A ≈ 14,5.

Cách 2:

Thực hiện phép tính

A = $\frac{54,11.6,95}{26,15}$ = $\frac{376,0645}{26,15}$ = 14,38105163…

Gạch chân dưới chữ số hàng phần mười của A được 14,38105163…

Chữ số liền kề bên phải của chữ số 3 vừa gạch chân là chữ số 8 > 5 nên thực hiện cộng thêm 1 vào chữ số vừa gạch chân và bỏ đi các chữ số phía sau.

Khi đó ta được số 14,4.

Vậy A ≈ 14,4.

Bài 8 trang 45 Toán lớp 7 Tập 1: Kết quả điểm môn Toán của Bích trong học kỳ 1 như sau:

Điểm đánh giá thường xuyên: 6; 8; 8; 9;

Điểm đánh giá giữa kì: 7

Điểm đánh giá cuối kì: 10.

Hãy tính điểm trung bình môn Toán của Bích và làm tròn đến hàng phần mười.

Lời giải:

Điểm trung bình môn Toán của Bích là: $\frac{6+8+8+9+7.2+10.3}{4+2+3}$ = $\frac{75}{9}$ = 8,333…

Gạch chân dưới chữ số hàng phần mười của 8,333… được 8,333…

Chữ số liền kề bên phải của chữ số 3 vừa gạch chân là chữ số 3 < 5 nên giữ nguyên chữ số vừa gạch chân và bỏ đi các chữ số phía sau.

Vậy điểm trung bình môn Toán của Bích xấp xỉ 8,3.

Lý thuyết Bài tập cuối chương 2

1. Biểu diễn thập phân của một số hữu tỉ

Với một số hữu tỉ $\frac{a}{b}$, ta chỉ có hai trường hợp sau:

Trường hợp 1: Nếu $\frac{a}{b}$ bằng một phân số thập phân thì kết quả của phép chia $\frac{a}{b}$ là số thập phân bằng với phân số thập phân đó.

Ví dụ:

$\frac{2}{5}=\frac{4}{10}=0,4$; $\frac{3}{25}=\frac{12}{100}=0,12$.

Khi đó, các số 0,4 và 0,12 được gọi là số thập phân hữu hạn.

Trường hợp 2: Nếu $\frac{a}{b}$ không bằng bất cứ phân số thập phân nào thì kết quả của phép chia $\frac{a}{b}$ không bao giờ dừng và có chữ số hoặc cụm chữ số sau dấu phẩy lặp đi lặp lại.

Ví dụ:

a) Ta thực hiện phép chia 5 : 12 = 0,41666…; số 6 được lặp đi lặp lại mãi mãi.

Khi đó, ta viết $\frac{5}{12}=0,\mathrm{41666...}=0,41\left(6\right)$.

b) Ta thực hiện phép chia 7 : 30 = 0,2333… ; chữ số 3 lặp đi lặp lại mãi mãi.

Khi đó, ta viết $\frac{7}{30}=0,\mathrm{2333...}=0,2\left(3\right)$.

Do đó các số 0,41(6); 0,2(3) gọi là số thập phân vô hạn tuần hoàn và chữ số lặp đi lặp lại như (6); (3) được gọi là chu kì.

Chú ý: Số 0,41(6) đọc là 0,41 chu kì 6 ; số 0,2(3) đọc là 0,2 chu kì 3.

• Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.

Ví dụ: $\frac{12}{25}=\frac{48}{100}=0,48$; $\frac{10}{9}=1,\left(1\right)$

2. Số vô tỉ

– Số thập phân vô hạn mà ở phần thập phân của nó không có một chu kì nào cả được gọi là số thập phân vô hạn không tuần hoàn.

– Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.

– Tập hợp các số vô tỉ kí hiệu là ?.

Ví dụ:

a) Với x² = 2 người ta tính được x = 1,414213562… là số thập phân vô hạn không tuần hoàn.

Vậy x = 1,414213562… là số vô tỉ.

b) Số Pi (π) là tỉ số giữa chu vi của một đường tròn với độ dài đường kính của đường tròn đó.

Người ta tính được π = 3,141592653… là số thập phân vô hạn không tuần hoàn.

Vậy π là một số vô tỉ.

3. Căn bậc hai số học

– Căn bậc hai số học của số a không âm là số x không âm sao cho x² = a.

Ta dùng kí hiệu $\sqrt{a}$ để chỉ căn bậc hai số học của a.

– Một số không âm a có đúng một căn bậc hai số học.

Chú ý:

– Số âm không có căn bậc hai số học.

– Ta có $\sqrt{a}$ ≥ 0 với mọi số a không âm.

– Với mọi số a không âm, ta luôn có ${\left(\sqrt{a}\right)}^2=a$, ví dụ như ${\left(\sqrt{2}\right)}^2=2$.

– Ta có $\sqrt{2}$ là độ dài đường chéo của một hình vuông có cạnh bằng 1.

Ví dụ: $\sqrt{4}=2$ ; $\sqrt{81}=9$ ; $\sqrt{0}=0$.

4. Tính căn bậc hai số học bằng máy tính cầm tay

Ta có thể tính giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số nguyên dương bằng máy tính cầm tay.

Ví dụ: Dùng máy tính cầm tay ta tính $\sqrt{8}$ và $\sqrt{2250}$ như sau:

Vậy $\sqrt{8}$ ≈ 2,828427125; $\sqrt{2250}$ ≈ 47,4341649.

5. Số thực và tập hợp các số thực

– Ta gọi chung số hữu tỉ và số vô tỉ là số thực.

– Tập hợp số thực được kí hiệu ℝ.

Cách viết x ∈ ℝ cho ta biết x là một số thực.

– Mỗi số thực chỉ có một trong hai dạng biểu diễn thập phân sau:

+ Dạng thập phân hữu hạn hay vô hạn tuần hoàn nếu số đó là số hữu tỉ.

+ Dạng thập phân vô hạn không tuần hoàn nếu số đó là số vô tỉ.

Ví dụ: Ta có các số 5; –3 ; 0,14 ; $-\frac{8}{7}$ ; $3\frac{1}{8}$ ; $\sqrt{11}$ ; π ; ….là các số thực.

Ta viết 5 ∈ ℝ ; –3 ∈ ℝ ; 0,14 ∈ ℝ ; $-\frac{8}{7}$ ∈ ℝ ; $3\frac{1}{8}$ ∈ ℝ; $\sqrt{11}$ ∈ ℝ ; π ∈ ℝ ; …

Chú ý: Trong các tập hợp đã học, tập hợp số thực là “rộng lớn” nhất bao gồm tất cả các số tự nhiên, số nguyên, số hữu tỉ và cả số vô tỉ.

– Trong tập hợp các số thực, ta cũng có các phép tính với các tính chất tương tự như các phép tính trong tập hợp các số hữu tỉ mà ta đã biết.

6. Thứ tự trong tập hợp các số thực

– Các số thập phân hữu hạn hoặc vô hạn đều có thể so sánh tương tự như so sánh hai số thập phân hữu hạn, đó là so sánh phần số nguyên, rồi đến phần thập phân thứ nhất, phần thập phân thứ hai, …

– Ta có thể so sánh hai số thực bằng cách so sánh hai số thập phân (hữu hạn hoặc vô hạn) biểu diễn chúng.

Do vậy: Với hai số thực x, y bất kì, ta luôn có hoặc x < y hoặc x > y hoặc x = y.

Chú ý: Với hai số thực dương a và b, ta có:

Nếu a > b thì $\sqrt{a}>\sqrt{b}$.

Ví dụ: So sánh hai số thực:

a) 5,(56) và 5,566;

b) $\sqrt{3}$ và 1,733;

c) –1,024 và –1,025;

d) $\sqrt{8}$ và 3.

Hướng dẫn giải

a) Số 5,(56) = 5,565656… < 5,566 (do phần thập phân thứ ba của hai số ta thấy 5 < 6).

Vậy 5,(56) < 5,566.

b) Ta có: $\sqrt{3}$ = 1,73205… < 1,733 (do phần thập phân thứ ba của hai số ta thấy 2 < 3).

Vậy $\sqrt{3}$ < 1,733.

c) Ta có: 1,024 < 1,025 (do phần thập phân thứ ba của hai số ta thấy 4 < 5)

Suy ra: –1,024 > –1,025.

Vậy –1,024 > –1,025.

d) Do 8 < 9 nên ta có $\sqrt{8}<\sqrt{9}$, tức là $\sqrt{8}$ < 3 (vì $\sqrt{9}$ = 3).

Vậy $\sqrt{8}$ < 3.

7. Trục số thực

Ta đã biết một hình vuông có cạnh bằng 1 có độ dài đường chéo là $\sqrt{2}.$

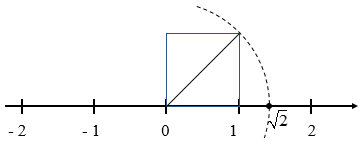
– Trên trục số ta biểu diễn được số vô tỉ $\sqrt{2}.$. Vì vậy, không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ, nghĩa là các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

Người ta chứng minh được rằng:

+ Mỗi số thực được biểu diễn bởi một điểm trên trục số

+ Ngược lại, mỗi điểm trên trục số biểu diễn một số thực.

Vì vậy, ta gọi trục số là trục số thực.

Chú ý:

– Điểm biểu diễn số thực x trên trục số được gọi là điểm x.

– Nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ví dụ: Ta có: $\sqrt{2}.$ = 1,414213562… < 1,5.

Vậy điểm $\sqrt{2}.$ nằm bên trái điểm 1,5 trên trục số nằm ngang.

8. Số đối của một số thực

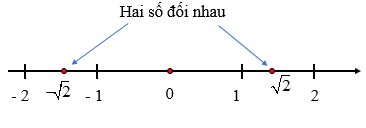
– Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này gọi là số đối của số kia.

– Số đối của số thực x kí hiệu là –x.

– Ta có x + (– x) = 0.

Ví dụ: Số đối của số $\sqrt{2}$ là $-\sqrt{2}$, số đối của $-\sqrt{2}$ là $\sqrt{2}$.

9. Giá trị tuyệt đối của một số thực

Giá trị tuyệt đối của một số thực x là khoảng cách từ điểm x đến điểm 0 trên trục số.

Giá trị tuyệt đối của một số thực x được kí hiệu là |x|.

Nhận xét: Ta có$\left|x\right|\text{ = }\left\{\begin{array}{c}x\text{ khi x > 0}\\ -x\text{ \hspace{0.17em}khi x < 0}\\ 0\text{ \hspace{0.17em}khi x =\hspace{0.17em} 0}\end{array}\right.$

Vậy giá trị tuyệt đối của một số thực x luôn là số không âm:

|x| ≥ 0 với mọi số thực x.

Ví dụ:

a)

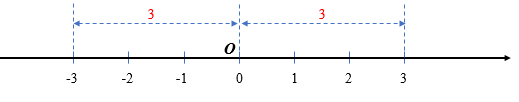
– Khoảng cách từ điểm –3 đến điểm 0 là 3 nên |–3| = 3.

– Khoảng cách từ điểm 3 đến gốc 0 là 3 nên |3| = 3.

b) Vì –2 < 0 nên |–2| = –(–2) = 2.

10. Làm tròn số

– Khi làm tròn một số thập phân đến hàng nào thì hàng đó gọi là hàng quy tròn.

– Muốn làm tròn số thập phân đến một hàng quy tròn nào đó, ta thực hiện các bước sau:

+ Gạch dưới chữ số thập phân của hàng quy tròn.

+ Nhìn sang chữ số ngay bên phải:

• Nếu chữ số đó lớn hơn hoặc bằng 5 thì tăng chữ số gạch dưới lên một đơn vị rồi thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân.

• Nếu chữ số đó nhỏ hơn 5 thì giữ nguyên chữ số gạch dưới và thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân.

Ví dụ :

a) Làm tròn số 32,506 đến hàng chục.

b) Làm tròn số –1,4257 đến hàng phần trăm.

Hướng dẫn giải

a) Làm tròn 32,506 đến hàng chục, ta có hàng quy tròn là chữ số 3.

Ta gạch dưới số 3: 32,506; nhìn sang chữ số ngay bên phải là chữ số 2 ở hàng đơn vị.

Mà 2 < 5.

Do đó ta giữ nguyên chữ số 3 đã gạch chân; thay chữ số 2 bởi số 0 và bỏ đi các chữ số 5, 0, 6 ở phần thập phân.

Vậy số 32,506 được làm tròn đến hàng chục là 30.

b) Làm tròn –1,4257 đến hàng phần trăm, ta có hàng quy tròn là chữ số 2.

Ta gạch dưới số 2: –1,4257; nhìn sang chữ số ngay bên phải là chữ số 5 ở hàng phần nghìn.

Mà 5 = 5.

Do đó ta tăng thêm 1 đơn vị vào chữ số 2 đã gạch chân; bỏ đi các chữ số 5, 7 ở phần thập phân.

Vậy số –1,4257 được làm tròn đến hàng phần trăm là –1,43.

– Do mọi số thực đều có thể viết dưới dạng số thập phân hữu hạn hoặc vô hạn nên để dễ nhớ, dễ ước lượng, dễ tính toán với các số thực có nhiều chữ số, người ta thường làm tròn số.

– Chú ý:

+ Ta phải viết một số dưới dạng thập phân trước khi làm tròn.

+ Khi làm tròn số thập phân ta không quan tâm đến dấu của nó.

Ví dụ:

a) Làm tròn số $\sqrt{2}$ đến hàng phần nghìn.

Ta viết biểu diễn thập phân của số $\sqrt{2}$là $\sqrt{2}$ = 1,414213562…

Áp dụng quy tắc làm tròn số ta có:

Số $\sqrt{2}$ = 1,414213562… được làm tròn đến hàng phần nghìn là 1,414.

b) Làm tròn số $-\frac{3}{11}$ đến hàng phần mười.

Ta viết biểu diễn thập phân của $-\frac{3}{11}$ là $-\frac{3}{11}=-0,\mathrm{272727...}$

Áp dụng quy tắc làm tròn số ta được:

Số $-\frac{3}{11}=-0,\mathrm{272727...}$ được làm tròn đến hàng phần mười là –0,3.

11. Làm tròn số căn cứ vào độ chính xác cho trước

– Cho số thực d, nếu khi làm tròn số a ta thu được số x thỏa mãn |a – x| ≤ d thì ta nói x là số làm tròn của số a với độ chính xác d.

– Chú ý:

+ Nếu độ chính xác d là số chục thì ta thường làm tròn a đến hàng trăm.

+ Nếu độ chính xác d là số phần nghìn thì ta thường làm tròn a đến hàng phần trăm, …

Ví dụ: Hãy làm tròn số:

a) Số 2,541 với độ chính xác d = 0,006;

b) Số –24 661 với độ chính xác d = 50;

c) Số $\sqrt{2}$ với độ chính xác d = 0,0005.

Hướng dẫn giải

a) Do độ chính xác đến hàng phần nghìn nên ta làm tròn số 2,541 đến hàng phần trăm và có kết quả là 2,54.

b) Do độ chính xác đến hàng chục nên ta làm tròn số –24 661 đến hàng trăm và có kết quả là –24 700.

c) Do độ chính xác đến hàng phần chục nghìn nên ta làm tròn số $\sqrt{2}$ đến hàng phần nghìn. Số $\sqrt{2}$ =1,414213562… được làm tròn đến hàng phần nghìn là 1,414.

12. Ước lượng các phép tính

Ta có thể áp dụng quy tắc làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí, đặc biệt là những sai sót do bấm nhầm nút khi sử dụng máy tính cầm tay.

Ví dụ: Áp dụng quy tắc làm tròn để ước lượng kết quả của các phép tính sau:

a) 6,23 + 5,76;

b) 50,1 . 49,8.

Hướng dẫn giải

a) Làm tròn đến hàng phần mười của mỗi số hạng ta được:

6,23 ≈ 6,2; 5,76 ≈ 5,8.

Khi đó 6,23 + 5,76 ≈ 6,2 + 5,8 = 12.

Vậy 6,23 + 5,76 ≈ 12.

b) Làm tròn đến hàng đơn vị mỗi thừa số ta có:

50,1 ≈ 50; 49,8 ≈ 50.

Khi đó 50,1 . 49,8 ≈ 50 . 50 = 2500.

Vậy 50,1 . 49,8 ≈ 2500.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Số vô tỉ. Căn bậc hai số học

Bài 2: Số thực. Giá trị tuyệt đối của một số thực

Bài 3: Làm tròn số và ước lượng kết quả

Bài 4: Hoạt động thực hành và trải nghiệm: Tính chỉ số đánh giá thể trạng BMI (Body mass index)

Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài tập cuối chương 2

Trắc nghiệm Ôn tập chương 2