Bài 9 trang 136 Toán 8 Tập 2 | Kết nối tri thức Giải Toán lớp 8

Lời giải Bài 9 trang 136 Toán 8 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

1 180 28/12/2023

Trang trước

Trang sau

Giải Toán 8 Bài tập ôn tập cuối năm

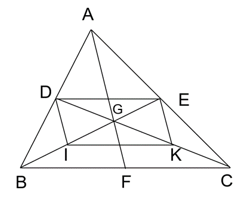
Bài 9 trang 136 Toán 8 Tập 2: Cho tam giác ABC. Các đường trung tuyến AF, BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của BG và CG.

a) Chứng minh rằng tứ giác DEKI là hình bình hành.

b) Biết AF = 6 cm. Tính độ dài các đoạn thẳng DI và EK.

Lời giải:

Bài 9 trang 136 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

a) Xét tam giác ABC có:

CD là đường trung tuyến của tam giác ABC nên D là trung điểm của AB

BE là đường trung tuyến của tam giác ABC nên E là trung điểm của AC

Do đó, DE là đường trung bình của tam giác ABC.

Suy ra DE // BC và $D E = \frac{1}{2} B C$ (1).

Tương tự, có IK là đường trung bình của tam giác GBC.

Suy ra IK // BC và $I K = \frac{1}{2} B C$ (2).

Từ (1) và (2), suy ra DE // IK và DE = IK.

Vậy DEKI là hình bình hành.

b) Có điểm G là trọng tâm của tam giác ABC.

Suy ra AG = $\frac{2}{3}$ AF = $\frac{2}{3} . 6$ = 4 cm.

Lại có E và K lần lượt là trung điểm của AC và CG nên EK là đường trung bình của tam giác CAG, do đó EK = $\frac{1}{2}$ AG = $\frac{1}{2} . 4$ = 2 cm.

Vì DEKI là hình bình hành nên DI = EK = 2 cm.

Xem thêm Lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 1 trang 135 Toán 8 Tập 2: Rút gọn các biểu thức sau: a) (2x + y)² + (5x – y)² + 2(2x + y)(5x – y);...

Bài 2 trang 135 Toán 8 Tập 2: Cho đa thức P = x² – y² + 6x + 9. a) Phân tích đa thức P thành nhân tử...

Bài 3 trang 135 Toán 8 Tập 2: Cho đa thức f(x) = x² – 15x + 56. a) Phân tích đa thức f(x) thành nhân tử. b) Tìm x sao cho f(x) = 0...

Bài 4 trang 135 Toán 8 Tập 2: Cho phân thức $P = \frac{2 x^{3} + 6 x^{2}}{2 x^{3} - 18 x}$ a) Viết điều kiện xác định và rút gọn phân thức P...